2024年海南省海口市部分学校6月份联考数学模拟试题(含答案)
文档属性
| 名称 | 2024年海南省海口市部分学校6月份联考数学模拟试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 759.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-08 22:27:10 | ||
图片预览



文档简介
2024年海口市部分学校6月份联考模拟试题
九年级数学学科试题
一、选择题(满分36分,每小题3分)
1、-2024的绝对值是( ) A.-2024 B. 2024 C. D.
2、计算的结果是( ) A. B. C. D.
3、如图是由5个大小相同的小正方体摆成的立体图形,
则它的左视图是( )
4、数据2060000000用科学计数法表示为( )A. B. C. D.
5、如图,将三角形的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为( )
A.10° B.15° C.20° D.25°
6、某商品原价为20元,连续两次降价后售价为8元,设平均降价率为,根据题意,
可列方程为( ). A. B. C. D.
7、分式方程的解是( )A. B. C. D.
8、为了加强学生的体育锻炼意识,某校定期举行体育竞技.在一次体育竞技中,该校初三10名学生的得分依次为39,40,38,39,37,38,36,39,40,39.则这组数据的众数和中位数分别是( )
A.38,39 B.39,38 C.39,39 D.39,40
9、如图,AB切⊙O于点B,连接OA交⊙O于点C,BD∥OA交⊙O于点D,
连接CD,若∠OCD=25 ,则∠A的度数为( )
A. B. C. D.
10、已知点 , 在反比例函数的图象上.若,则( )
A. B. C. D.
11、 如图,在平面直角坐标系中,菱形OABC的边长为2,点B在轴的正半轴上,且∠AOC=60 ,将菱形OABC绕原点O逆时针方向旋转60 ,得到四边形OA’B’C’点A’与点C重合,则点B’的坐标是( )
A. B. C. D.
12、边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),
则图中阴影部分的面积为( ).
A.9 B.12 C.15 D.18
二、填空题(本大题满分12分,每小题3分)
13、因式分解: .
14、如图,在△ABC中,∠B=40 ,∠C=50 .通过观察尺规作图的痕迹,则∠DAE= .
15、一次函数的值随值的增大而减少,则常数的取值范围是 .
16、如图,标号为①,②,③,④的四个直角三角形和标号为⑤的正方形恰好拼成对角互补的四边形ABCD,相邻图形之间互不重叠也无缝隙,①和②分别是等腰Rt△ABE和等腰Rt△BCF,③和④分别是Rt△CDG和Rt△DAH,⑤是正方形EFGH,若EF=3cm,AE+FC=11cm,则BE的长是 cm;若,则tan∠DAH的值是 .
三、解答题(本大题满分72分)
17、(12分)(1) (2)化简:
A型 B型 销售额
上周 2辆 3辆 98万元
本周 3辆 1辆 91万元
18、(10分)近年来,新能源汽车深受人们的喜爱. 某汽车专卖店两周销售、两种型号的新能源汽车的情况如右表:请根据表格数据,求出每辆型号车的售价各为多少万元.
19、(10分)某校为了庆祝2022年元旦,举行了书法比赛,赛后整理参赛同学的成绩,并制作成图表如下:
请根据以上图表提供的信息,解答下列问题:
这次共调查了 名学生;表中的数
m= ,n= .
(2)请在图中补全频数分布直方图.
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 .
(4)如果比赛成绩在80分以上(含80分)可获得奖励,那么获奖概率是 .
20、(10分)河边新建成了一座美丽的大桥.某学校数学兴趣小组组织了一次测桥墩高度的活动,如图,桥墩刚好在坡度i=1:的斜坡BC边,斜坡BC长为48米,在点D处测得桥墩最高点A的仰角为35 ,CD平行于水平线BM,CD长为16米. (1)∠CBM= ,∠BAD= .(2)求点C到直线BM的距离;
(3)求桥墩AB的高(结果保留位小数).(,,,)
21、(15分)菱形ABCD中,AB=5,点F是AD边上的点,点Q是AB边上的点.
(1)如图1,若点F是AD的中点,CQ⊥AB,连接CF并延长交BA的延长线于点P,连接QF,
①求证:△PAF≌△CDF;②判定△FCQ的形状,并说明理由;(2)若菱形面积为20,将菱形ABCD沿CQ翻折,点B的对应点为点E. ①如图2,当点E落在BA边的延长线上时,连接BD,交CQ于R,交EC于点M,求的值;
②如图3,当CE⊥AD,垂足为点F,交AD于点N,求四边形CFNQ的面积.
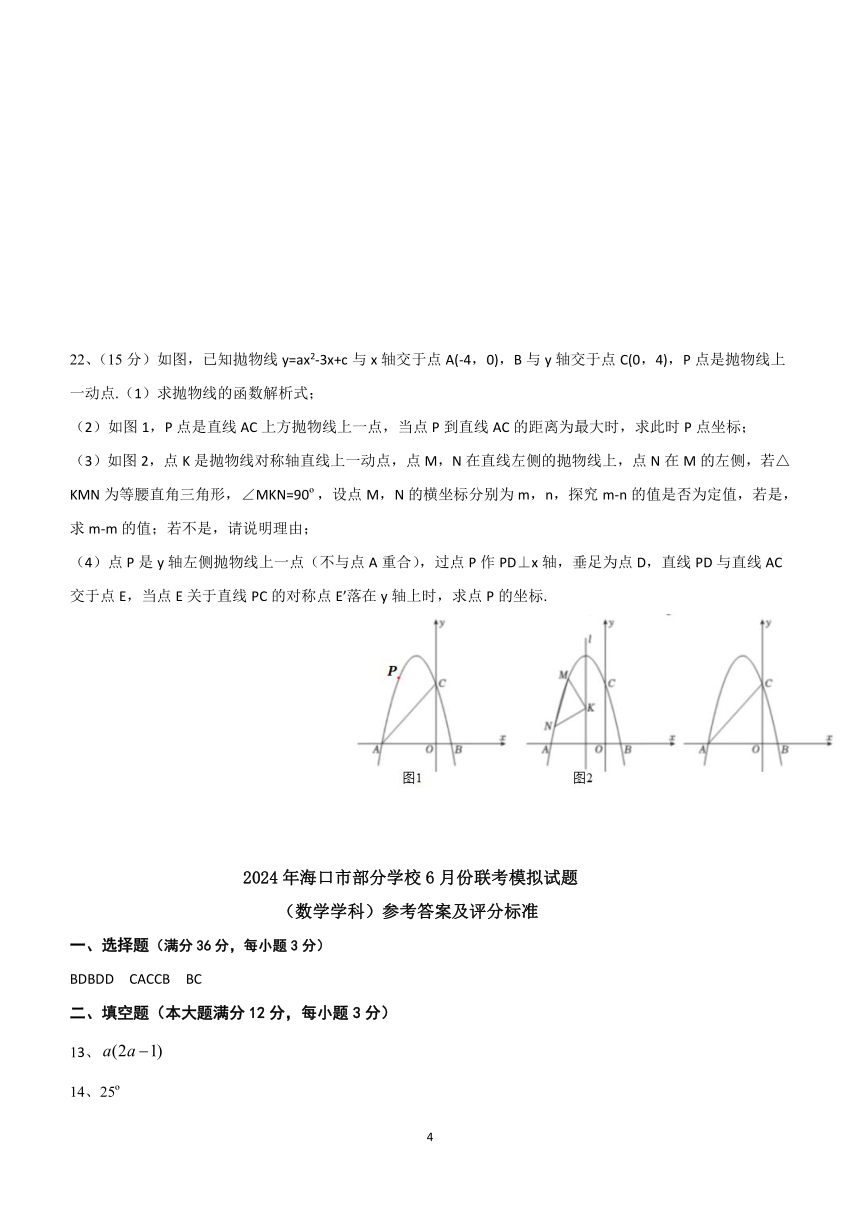
22、(15分)如图,已知拋物线y=ax2-3x+c与x轴交于点A(-4,0),B与y轴交于点C(0,4),P点是抛物线上一动点.(1)求抛物线的函数解析式;
(2)如图1,P点是直线AC上方抛物线上一点,当点P到直线AC的距离为最大时,求此时P点坐标;
(3)如图2,点K是抛物线对称轴直线上一动点,点M,N在直线左侧的抛物线上,点N在M的左侧,若△KMN为等腰直角三角形,∠MKN=90 ,设点M,N的横坐标分别为m,n,探究m-n的值是否为定值,若是,求m-m的值;若不是,请说明理由;
(4)点P是y轴左侧抛物线上一点(不与点A重合),过点P作PD⊥x轴,垂足为点D,直线PD与直线AC交于点E,当点E关于直线PC的对称点E’落在y轴上时,求点P的坐标.
2024年海口市部分学校6月份联考模拟试题
(数学学科)参考答案及评分标准
一、选择题(满分36分,每小题3分)
BDBDD CACCB BC
二、填空题(本大题满分12分,每小题3分)
13、
14、25
15、
16、4 3 (2分+1分=3分)
三、解答题(本大题满分72分)
17、(12分)(1) (2)化简:
= ………………4分 =…………4分
= …………………………6分 =………………………………6分
A型 B型 销售额
上周 2辆 3辆 98万元
本周 3辆 1辆 91万元
18、(10分)近年来,新能源汽车深受人们的喜爱. 某汽车专卖店两周销售、两种型号的新能源汽车的情况如右表:请根据表格数据,求出每辆型号车的售价各为多少万元.
解:设A售价为x元,B为y元,得
………………………………6分
得……………………………………9分
答:A售价为25元,B为16元…………10分
19、(1)200 90 0.3………………4分
(2)…………………………………………6分
(3)54 ……………………………………8分
(4)40%……………………………………10分
20、(10分)(1)30 55 ……………………4分
(2)作CF⊥BM于F
则CF==24
即C到BM的距离是24米………………………………7分
作CE⊥AB于E
则CE=BF=
在△ADE中,AE=DE·tan35 =(16+24)·0.7=28
∴AB=AE+BE=28+24≈72.4米………………………………10分
21、(15分)
(1)①证明:∵F为AD中点,
∴AF=DF,
∵四边形ABCD是菱形,
∴AB∥CD,
∴∠P=∠FCD,
又∵∠AFP=∠DFC,
∴△PAF≌△CDF(AAS);……………………4分
②解:△FCQ是等腰三角形.
理由如下:∵△PAF≌△CDF,
∴PF=CF,
∵CQ⊥AB,
∴∠CQP=90°,
∴QF是Rt△CQF斜边上的中线,
∴QF=FC=PC,
∴△FCQ是等腰三角形;……………………6分
(2)解:①∵点B与点E关于CQ对称,
∴CQ⊥BE,QE=QB,
∵S菱形ABCD=20,AB=7,
∴CQ=20÷5=4,
在△BCQ中,根据勾股定理可得:BQ=,
∴QE=3,AQ=4﹣3=2,
∴AE=7﹣2=1,
∵四边形ABCD是菱形,
∴AB∥CD,AD∥CB,
∴△BQR∽△DCR,△FDM∽△CBM,
∴,,,
设AF=k,则FD=5k,
则AD=AF+FD=k+5k=6k,
∴,即,
∴DR=BD,
∵DF=,BC=5,
∴,
∴,
∴BM=BD,
∴,
即的值为;………………………………………………11分
②如图3,过点Q作QH⊥CE于H,
∵CE⊥AD,AD∥BC,
∴∠BCE=90°,
由折叠可知:CE=BC=6,∠BCH=,
∴CH=QH,∠E=∠B=∠D,
∵S菱形ABCD=20,AD=2,
∴CF=4,
∴EF=1,
在Rt△CFD中,由勾股定理得:FD=,
∵∠E=∠D,∠EFN=∠DFC=90°,
∴△EFN∽△DFC,
∴,
∴NF=,
∴S△NEF=NF EF=,
∵QH⊥CE,AD⊥CE,
∴NF∥QH,
∴△ENF∽△EQH,
∴,
设EH=3k,则QH=CH=5k,
∵EH+CH=CE=5,即3k+6k=5,
∴k=,
∴QH=4k=,
∴S△QCE=CE QH=,
∴S四边形CFNQ=S△QCE﹣S△ENF=.……………………………………15分
22、(1)……………………………………4分
(2)作PH∥y轴于H
设P(m, -m2-3m+4)
由A、C点可得yAC=x+4
则H(m,m+4)
∴PH= -m2-3m+4-(m+4)=-m2-4m
∴S△APC==-2m2-8m=-2(m+2)2+8
∴当m=-2时,S△APC有最大值,此时,P点到AC距离最大
∴P(-2,6)……………………………………7分
(3)∵点M,N的横坐标分别为m,n,M(m,-m2-3m+4),N(n,-n2-3n+4)
设直线与x轴交于点Q,过M作MH⊥直线于H,过N作NG⊥直线于G,
∴∠KHM=∠NGK=90°,△KMN为等腰直角三角形,∠MKN=90 , KM = NK,
∠MKH+∠NKG=∠KNG +∠NKG=90
∴∠MKH=∠KNG
∴△KMH≌△NKG(AAS),
∴MH-=KG ,KH=NG
∵GH=KH+KG=NG+MH
∴-m2- 3m+4-(-n2-3n+4)=()+()
m2+2m-n2-3n-3=0
(m+1)2-(n+2)2=0
(m+1+n+2)(m+1-n-2)=0
∴m-m=1
∴m-n的值是定值,m-n=1…………………………12分
(4)当点P在第二象限时(如图)
连接PE’,可得四边形PECE’是菱形
作PM⊥y轴于M
∴PE=PE’PM
∴-m2-3m+4-(m+4)=-m
∴m=-4+
∴P1(-4+,-2+5)………………………………14分
当点P在第三象限时(如图),
同理可得P2(-4-,-2-5)……………………15分
九年级数学学科试题
一、选择题(满分36分,每小题3分)
1、-2024的绝对值是( ) A.-2024 B. 2024 C. D.
2、计算的结果是( ) A. B. C. D.
3、如图是由5个大小相同的小正方体摆成的立体图形,
则它的左视图是( )
4、数据2060000000用科学计数法表示为( )A. B. C. D.
5、如图,将三角形的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为( )
A.10° B.15° C.20° D.25°
6、某商品原价为20元,连续两次降价后售价为8元,设平均降价率为,根据题意,
可列方程为( ). A. B. C. D.
7、分式方程的解是( )A. B. C. D.
8、为了加强学生的体育锻炼意识,某校定期举行体育竞技.在一次体育竞技中,该校初三10名学生的得分依次为39,40,38,39,37,38,36,39,40,39.则这组数据的众数和中位数分别是( )
A.38,39 B.39,38 C.39,39 D.39,40
9、如图,AB切⊙O于点B,连接OA交⊙O于点C,BD∥OA交⊙O于点D,
连接CD,若∠OCD=25 ,则∠A的度数为( )
A. B. C. D.
10、已知点 , 在反比例函数的图象上.若,则( )
A. B. C. D.
11、 如图,在平面直角坐标系中,菱形OABC的边长为2,点B在轴的正半轴上,且∠AOC=60 ,将菱形OABC绕原点O逆时针方向旋转60 ,得到四边形OA’B’C’点A’与点C重合,则点B’的坐标是( )
A. B. C. D.
12、边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),
则图中阴影部分的面积为( ).
A.9 B.12 C.15 D.18
二、填空题(本大题满分12分,每小题3分)
13、因式分解: .
14、如图,在△ABC中,∠B=40 ,∠C=50 .通过观察尺规作图的痕迹,则∠DAE= .
15、一次函数的值随值的增大而减少,则常数的取值范围是 .
16、如图,标号为①,②,③,④的四个直角三角形和标号为⑤的正方形恰好拼成对角互补的四边形ABCD,相邻图形之间互不重叠也无缝隙,①和②分别是等腰Rt△ABE和等腰Rt△BCF,③和④分别是Rt△CDG和Rt△DAH,⑤是正方形EFGH,若EF=3cm,AE+FC=11cm,则BE的长是 cm;若,则tan∠DAH的值是 .
三、解答题(本大题满分72分)
17、(12分)(1) (2)化简:
A型 B型 销售额
上周 2辆 3辆 98万元
本周 3辆 1辆 91万元
18、(10分)近年来,新能源汽车深受人们的喜爱. 某汽车专卖店两周销售、两种型号的新能源汽车的情况如右表:请根据表格数据,求出每辆型号车的售价各为多少万元.
19、(10分)某校为了庆祝2022年元旦,举行了书法比赛,赛后整理参赛同学的成绩,并制作成图表如下:
请根据以上图表提供的信息,解答下列问题:
这次共调查了 名学生;表中的数
m= ,n= .
(2)请在图中补全频数分布直方图.
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 .
(4)如果比赛成绩在80分以上(含80分)可获得奖励,那么获奖概率是 .
20、(10分)河边新建成了一座美丽的大桥.某学校数学兴趣小组组织了一次测桥墩高度的活动,如图,桥墩刚好在坡度i=1:的斜坡BC边,斜坡BC长为48米,在点D处测得桥墩最高点A的仰角为35 ,CD平行于水平线BM,CD长为16米. (1)∠CBM= ,∠BAD= .(2)求点C到直线BM的距离;
(3)求桥墩AB的高(结果保留位小数).(,,,)
21、(15分)菱形ABCD中,AB=5,点F是AD边上的点,点Q是AB边上的点.
(1)如图1,若点F是AD的中点,CQ⊥AB,连接CF并延长交BA的延长线于点P,连接QF,
①求证:△PAF≌△CDF;②判定△FCQ的形状,并说明理由;(2)若菱形面积为20,将菱形ABCD沿CQ翻折,点B的对应点为点E. ①如图2,当点E落在BA边的延长线上时,连接BD,交CQ于R,交EC于点M,求的值;
②如图3,当CE⊥AD,垂足为点F,交AD于点N,求四边形CFNQ的面积.
22、(15分)如图,已知拋物线y=ax2-3x+c与x轴交于点A(-4,0),B与y轴交于点C(0,4),P点是抛物线上一动点.(1)求抛物线的函数解析式;
(2)如图1,P点是直线AC上方抛物线上一点,当点P到直线AC的距离为最大时,求此时P点坐标;
(3)如图2,点K是抛物线对称轴直线上一动点,点M,N在直线左侧的抛物线上,点N在M的左侧,若△KMN为等腰直角三角形,∠MKN=90 ,设点M,N的横坐标分别为m,n,探究m-n的值是否为定值,若是,求m-m的值;若不是,请说明理由;
(4)点P是y轴左侧抛物线上一点(不与点A重合),过点P作PD⊥x轴,垂足为点D,直线PD与直线AC交于点E,当点E关于直线PC的对称点E’落在y轴上时,求点P的坐标.
2024年海口市部分学校6月份联考模拟试题
(数学学科)参考答案及评分标准
一、选择题(满分36分,每小题3分)
BDBDD CACCB BC
二、填空题(本大题满分12分,每小题3分)
13、
14、25
15、
16、4 3 (2分+1分=3分)
三、解答题(本大题满分72分)
17、(12分)(1) (2)化简:
= ………………4分 =…………4分
= …………………………6分 =………………………………6分
A型 B型 销售额
上周 2辆 3辆 98万元
本周 3辆 1辆 91万元
18、(10分)近年来,新能源汽车深受人们的喜爱. 某汽车专卖店两周销售、两种型号的新能源汽车的情况如右表:请根据表格数据,求出每辆型号车的售价各为多少万元.
解:设A售价为x元,B为y元,得
………………………………6分
得……………………………………9分
答:A售价为25元,B为16元…………10分
19、(1)200 90 0.3………………4分
(2)…………………………………………6分
(3)54 ……………………………………8分
(4)40%……………………………………10分
20、(10分)(1)30 55 ……………………4分
(2)作CF⊥BM于F
则CF==24
即C到BM的距离是24米………………………………7分
作CE⊥AB于E
则CE=BF=
在△ADE中,AE=DE·tan35 =(16+24)·0.7=28
∴AB=AE+BE=28+24≈72.4米………………………………10分
21、(15分)
(1)①证明:∵F为AD中点,
∴AF=DF,
∵四边形ABCD是菱形,
∴AB∥CD,
∴∠P=∠FCD,
又∵∠AFP=∠DFC,
∴△PAF≌△CDF(AAS);……………………4分
②解:△FCQ是等腰三角形.
理由如下:∵△PAF≌△CDF,
∴PF=CF,
∵CQ⊥AB,
∴∠CQP=90°,
∴QF是Rt△CQF斜边上的中线,
∴QF=FC=PC,
∴△FCQ是等腰三角形;……………………6分
(2)解:①∵点B与点E关于CQ对称,
∴CQ⊥BE,QE=QB,
∵S菱形ABCD=20,AB=7,
∴CQ=20÷5=4,
在△BCQ中,根据勾股定理可得:BQ=,
∴QE=3,AQ=4﹣3=2,
∴AE=7﹣2=1,
∵四边形ABCD是菱形,
∴AB∥CD,AD∥CB,
∴△BQR∽△DCR,△FDM∽△CBM,
∴,,,
设AF=k,则FD=5k,
则AD=AF+FD=k+5k=6k,
∴,即,
∴DR=BD,
∵DF=,BC=5,
∴,
∴,
∴BM=BD,
∴,
即的值为;………………………………………………11分
②如图3,过点Q作QH⊥CE于H,
∵CE⊥AD,AD∥BC,
∴∠BCE=90°,
由折叠可知:CE=BC=6,∠BCH=,
∴CH=QH,∠E=∠B=∠D,
∵S菱形ABCD=20,AD=2,
∴CF=4,
∴EF=1,
在Rt△CFD中,由勾股定理得:FD=,
∵∠E=∠D,∠EFN=∠DFC=90°,
∴△EFN∽△DFC,
∴,
∴NF=,
∴S△NEF=NF EF=,
∵QH⊥CE,AD⊥CE,
∴NF∥QH,
∴△ENF∽△EQH,
∴,
设EH=3k,则QH=CH=5k,
∵EH+CH=CE=5,即3k+6k=5,
∴k=,
∴QH=4k=,
∴S△QCE=CE QH=,
∴S四边形CFNQ=S△QCE﹣S△ENF=.……………………………………15分
22、(1)……………………………………4分
(2)作PH∥y轴于H
设P(m, -m2-3m+4)
由A、C点可得yAC=x+4
则H(m,m+4)
∴PH= -m2-3m+4-(m+4)=-m2-4m
∴S△APC==-2m2-8m=-2(m+2)2+8
∴当m=-2时,S△APC有最大值,此时,P点到AC距离最大
∴P(-2,6)……………………………………7分
(3)∵点M,N的横坐标分别为m,n,M(m,-m2-3m+4),N(n,-n2-3n+4)
设直线与x轴交于点Q,过M作MH⊥直线于H,过N作NG⊥直线于G,
∴∠KHM=∠NGK=90°,△KMN为等腰直角三角形,∠MKN=90 , KM = NK,
∠MKH+∠NKG=∠KNG +∠NKG=90
∴∠MKH=∠KNG
∴△KMH≌△NKG(AAS),
∴MH-=KG ,KH=NG
∵GH=KH+KG=NG+MH
∴-m2- 3m+4-(-n2-3n+4)=()+()
m2+2m-n2-3n-3=0
(m+1)2-(n+2)2=0
(m+1+n+2)(m+1-n-2)=0
∴m-m=1
∴m-n的值是定值,m-n=1…………………………12分
(4)当点P在第二象限时(如图)
连接PE’,可得四边形PECE’是菱形
作PM⊥y轴于M
∴PE=PE’PM
∴-m2-3m+4-(m+4)=-m
∴m=-4+
∴P1(-4+,-2+5)………………………………14分
当点P在第三象限时(如图),
同理可得P2(-4-,-2-5)……………………15分
同课章节目录
