2.4三角形的中位线课件

课件22张PPT。 三角形的中位线湘教版 八年级下册
如右图，A、B两点被池塘隔开，现在要测量出A、B两点间的距离 ，但又无法直接去测量，怎么办？
这时，在A、B外选一点C，连结AC和BC，并分别找出AC和BC的中点D、E，如果能测量出DE的长度，也就能知道AB的距离了。
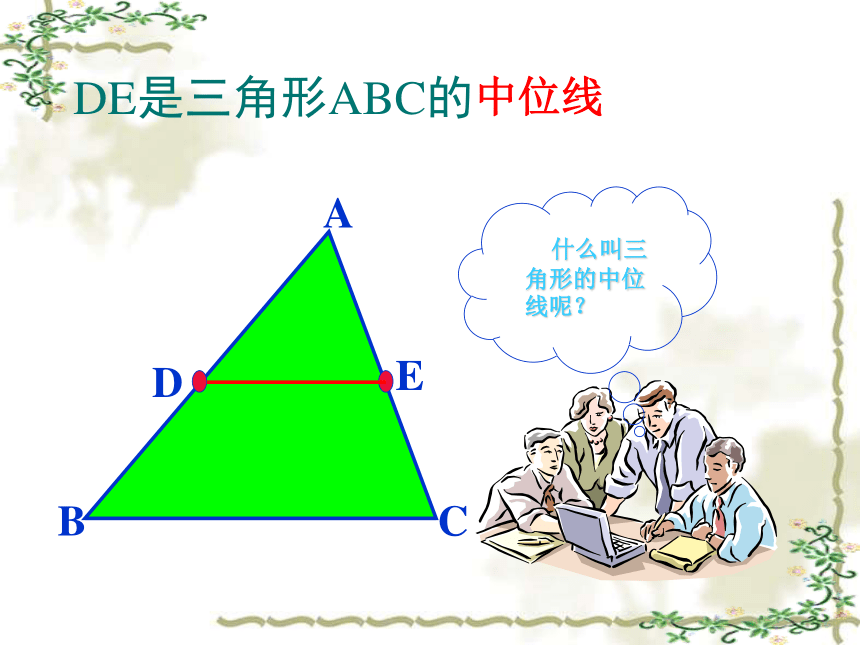
这是什么道理呢？今天这堂课我们就要来探究其中的学问。DEDE是三角形ABC的中位线三角形的中位线 连接三角形两边中点的线段叫做三角形的中位线。画出三角形的所有中线并说出中位线和中线的区别.DEF三角形中位线的两个端点是三角形两边
的中点，而三角形中线一端点是三角形
的顶点、另一端点是三角形这个顶点所
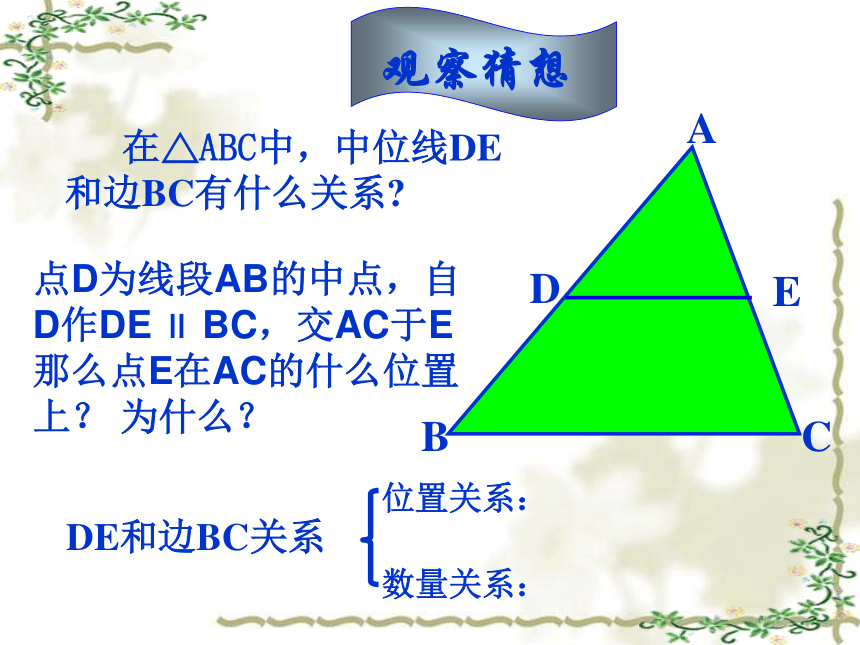
对的边的中点观察猜想 在△ABC中，中位线DE和边BC有什么关系?DE和边BC关系数量关系：位置关系：点D为线段AB的中点，自D作DE ∥ BC，交AC于E那么点E在AC的什么位置上？ 为什么？利用橡皮筋定在木板上，
验证你的观查和猜想：
①拖动点A，三角形形状变化了，
其中什么不变？
②三角形中位线DE与第三边BC的
位置关系怎么样？
它们有什么样的数量关系？
拖动点B，C呢？结论：三角形的中位线
平行于第三边，
并且等于它的一半.这个结论是否具有普遍性，还需要从理论上加以证明。
请同学们思考怎样来证明这个结论。已知：在△ABC 中，DE是△ABC 的中位线
求证：DE ∥ BC，且DE=1/2BC . 证法一：以点E为旋转中心，
把△ ADE绕点E旋转180゜，
得到△ CFE，则D，E，F同在
一直线上DE=EF，
且△ ADE≌ △ CFE
∴∠ADE=∠F，AD=CF，
∴AB∥CF。
又∵BD=AD=CF，
∴四边形BCFD是平行四边形
∴DE ∥ BC 且 DE=1/2BC
CEDFBA返回
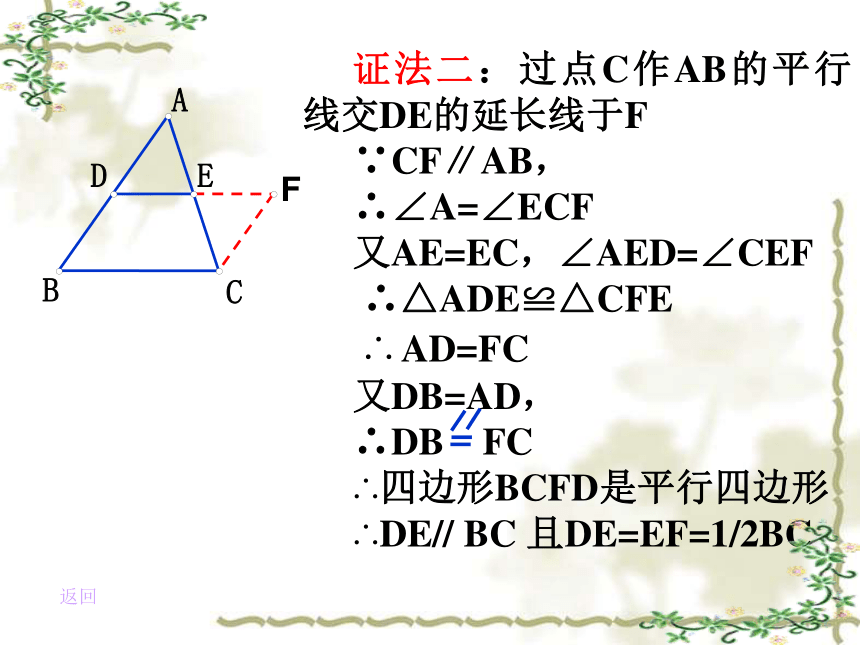
证法三：延长DE 到 F，使EF=DE
连结CF、AF、DC。
∵AE=EC，DE=EF
∴四边形ADCF是平行四边形
∴AD平行且等于FC
又D为AB中点，∴DB平行且等于FC
所以，四边形BCFD是平行四边形
∴DF平行且等于BC
又∵DE=1/2 DF，
∴DE ∥ BC 且 DE=1/2BC
已知：在△ABC 中，DE是△ABC 的中位线
求证：DE ∥ BC，且DE=1/2BC . 三角形的中位线的定理 三角形的中位线平行于第三边，并且等于它的一半用符号语言表示定理的用途：
i）证明平行问题
ii）证明一条线段是另一条线段的2倍或1/2
1、如图：在△ABC中，DE是中位线
（1）∠ADE=60°，则∠B= 度
（2）若BC=8cm，则DE= cm
2、已知三角形三边分别为6、8、10，
连结各边中点所成三角形的周长为 。
如右图，A、B两点被池塘隔开，现在要测量出A、B两点间的距离 ，但又无法直接去测量，怎么办？
这时，在A、B外选一点C，连结AC和BC，并分别找出AC和BC的中点D、E，如果能测量出DE的长度，也就能知道AB的距离了。
如果DE=20m，那么A、B两点的距离是多少？为什么？梯形ABCD中AD∥BC，
对角线AC、BD相交于点O，
A’、B’、C’、D’分别是
AO、BO、CO、DO中点，
则四边形A’B’C’D’是 ；
若梯形ABCD周长为10，
则四边形A’B’C’D’的周长为 。
例 求证：顺次连结四边形四条边的中点，所得的四边形是平行四边形.已知：如图，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点。
求证：四边形EFGH是平行四边形。思考：平行四边形菱形矩形变式练习正方形平行四边形菱形菱形矩形正方形总结不相等且不互相垂直的四边形各边中点
组成___________对角线平行四边形互相垂直的四边形各边中点组成______矩形相等的四边形各边中点组成_____菱形相等且互相垂直的四边形各边中点
组成_______正方形梳理 回放1、三角形中位线是三角形中一种重要的线段，它与三角形中线不同。
2、三角形的中位线定理
3、在这节课中我们一起经过实验、探索，发现了三角形中位线定理，其中学会了一种很重要的探究问题的方法。1. 如图,AF=FD=DB,AG=GB=EC,FG∥DE∥BC,PE=1.5,则BC= ———选作题
已知：如图2，E、F分别是AC、BD的中点，
CD≧AB，E、F不都是对角线的交点
求证： EF＞1/2（CD－AB）