相似三角形的判定
图片预览






文档简介
(共26张PPT)
类比的方法应在经验科学中占很高的地位,而且科学家也曾按照这种推论方法获得很重要的结果。
——黑格尔
(1770—1831)德国著名哲学家
24.3相似三角形
——2.相似三角形的判定(2)
问题1:相似三角形的有关概念
(1). 三个角对应_____ 、三条边对应_______的两个三角形叫做相似三角形
(2).相似三角形的对应角 _____,对应边________ .
(3).相似比等于____的两个三角形全等.
问题2:我们已经有哪些判别两三角形相似的方法?
(1)相似三角形的定义
(2)两角对应相等的两个三角形相似。
相等
成比例
相等
成比例
1
一、复习提问,类比猜想
一、复习提问,类比猜想
问题3 :全等三角形有哪些判定方法
ASA ( AAS) SAS SSS
问题4:类比三角形全等的判定,你认为可能还有哪些方法能判定两个三角形相似 (请同桌讨论,大胆猜想)
猜想二:三边对应成比例的两个三角形相似
猜想一:两边对应成比例且夹角相等的两个三 角形相似
二、设计方案,验证结论
猜想二:
三边对应相等的两个三角形相似
猜想一:
两边对应成比例且夹角相等的两个三角形相似
1 、请分组设计猜想一或猜想二的验证方案
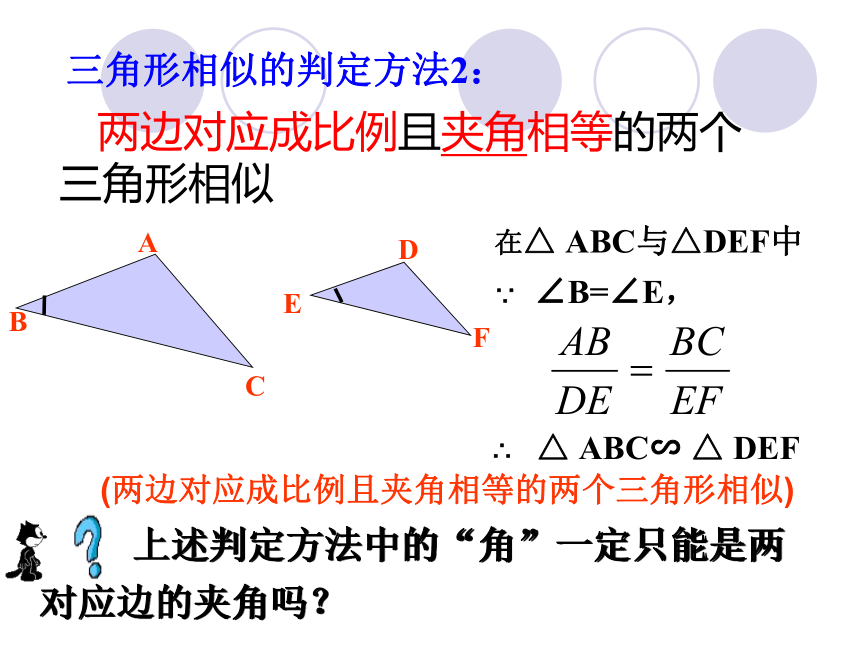
三角形相似的判定方法2:
两边对应成比例且夹角相等的两个
三角形相似
A
B
C
在△ ABC与△DEF中
∵ ∠B=∠E,
D
E
F
∴ △ ABC∽ △ DEF
(两边对应成比例且夹角相等的两个三角形相似)
上述判定方法中的“角”一定只能是两对应边的夹角吗?
我爱思考
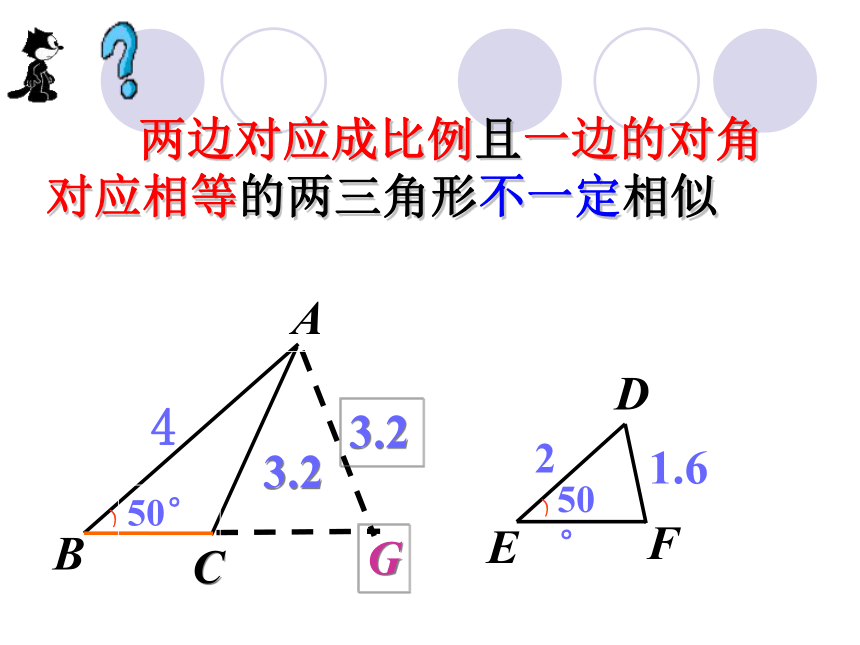
想一想:在上述问题中如果这个角是这两条边中其中一条边的对角呢,两个三角形还一定相似吗?(小组内交流)
G
3.2
C
3.2
50°
)
4
A
B
2
1.6
50°
)
E
D
F
两边对应成比例且一边的对角对应相等的两三角形不一定相似
C
A
B
C'
A'
B'
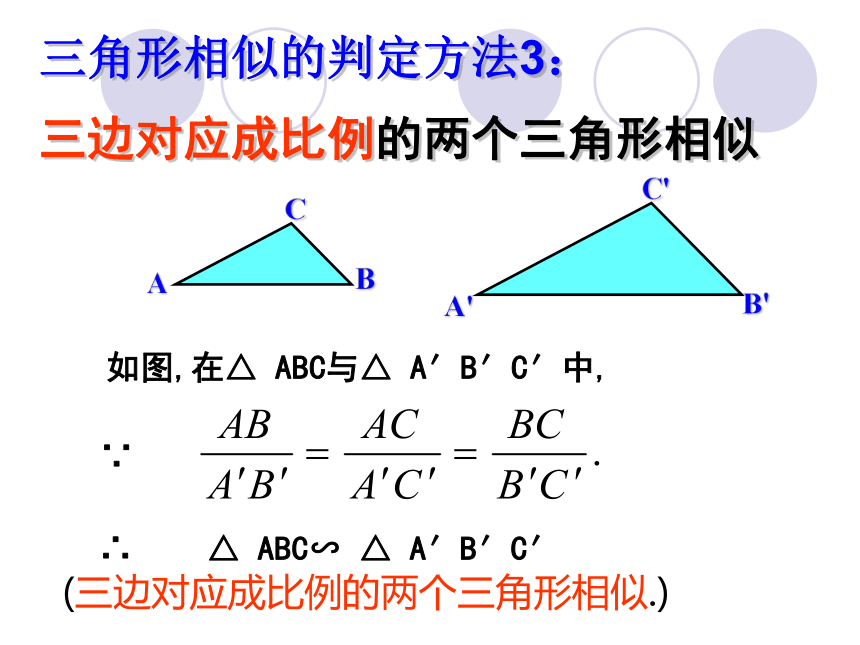
三边对应成比例的两个三角形相似
三角形相似的判定方法3:
如图,在△ ABC与△ A′B′C′中,
∴ △ ABC∽ △ A′B′C′
(三边对应成比例的两个三角形相似.)
∵
二、归纳概括,得出结论
方法4: 三边对应成比例的两个三角形相似
方法3: 两边对应成比例且夹角相等的两
个三角形相似
我们已经有哪些判别两三角形相似的方法?
方法1: 相似三角形的定义
方法2: 两角对应相等的两个三角形相似。
已知,如图,要使△ABC∽△ACD,需要添加几个条件?是 ( )
已知,如图,要使△ABE∽△ACD,需要添加几个条件?是( )
例3 证明:图中△AEB和△FEC相似.
证明 ∵
,
∴
∴ △AEB∽△FEC(如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似).
∵ ∠AEB=∠FEC,
依据下列各组条件,证明△ABC和△A’B’C’相似
∠A=40° , AB=8, AC=15,
∠A’=40 °,A’B’=16,A’C’=30.
三.应用新知,解决问题
证明:
∴ △ACD∽△ABC(两边对应成比例且夹角相等的两个三角形相似).
如图,D在△ABC的AB边上AD=1,BD=2,
AC= .问:△ACD与△ABC相似吗?为什么?
A
B
C
D
答: △ACD∽△ABC
例4 在△ABC和△A′B′C′中,已知: AB=6cm,BC=8cm,AC=10cm,A′B′=18cm,B′C′=24cm,A′C′=30cm.试证明△ABC与△A′B′C′相似.
证明 ∵
,
∴
∴ △ABC∽△A′B′C′(三边对应成比例的两个三角形相似).
依据下列各组条件,证明△ABC和△A′B′C′相似
AB=10cm,BC=8cm,AC=16cm,
A′B′=16cm,B′C′=12.8cm,A′C ′=25.6cm
例6. 如图,在矩形ABCD中,AB=8,AD=4,在AB上取一点M,使AM=2,连接DM交AC于N.
(1)图中DM与AC具备怎样的位置关系?试说明理由。
(2)写出和△ADC相似的三角形(除△ABC外)。
答:(1)DM⊥AC
证明:∵在矩形ABCD中,
∠DAM= ∠CDA=90°,
DC=AB=8,
,
A
B
C
D
M
N
∴
∴△CDA∽ △DAM
∴∠1=∠2
∵∠2+∠3=90°
∴∠1+∠3=90°
∴DM⊥AC
(2)和△ADC相似的三角形有:
△MAD, △MNA, △AND, △DNC
8
4
2
4
8
1
2
3
∴∠AND=90°
下面图中的两个三角形是否相似? 请说说你的理由:
C
A
4
5
5
E
F
B
4
四.巩固新知,熟能生巧
如图,△ ABC与△ A′B′C′相似吗
你用什么方法来支持你的判断
∴△ ABC∽△ A′B′C′
(三边对应成比例的两个三角形相似.)
C
B
A
A′
B′
C′
解:如图,设小正方形的边长为1,由勾股定理可得:
答:这两个三角形相似。
你还有不同的证法吗?
五、积累总结,知识升华
方法3: 三边对应相等的两个三角形相似
方法2: 两边对应成比例且夹角相等的两个三角形相 似
1、三角形相似的判定方法有哪些?
(定义法: 对应角相等,对应边成比例的两个三角形相似)
方法1: 两角对应相等的两个三角形相似。
六、积累总结,知识升华
2、三角形全等、相似常用判别方法的比较:
三角形全等的判别 三角形相似的判别
ASA(AAS) 两角对应相等
SSS 三边对应成比例
SAS 两边对应成比例且夹角相等
六、积累总结,知识升华
2、在应用三角形相似的判定方法2时要注意什么问题?
3、通过本节课的学习你体会到了哪些重要的数学思想?
从特殊到一般、类比
必须是两边的夹角,而非对角
如图,△ABC中,AB=4,AC=6,点D是AB边上一点,且AD=2,在AC边上找一点E,使得以A、D、E为顶点的三角形与△ABC相似。并求出AE的长度。
A
B
C
D
E1
E2
AE的长度为3或4/3
有一池塘, 周围都是空地. 如果要测量池塘两端A、B间的距离, 你能利用本节课所学的知识解决这个问题吗
A
B
D
E
C
生活中的应用)
C
E
D
B
A
若:
试说明 :
(1)∠ABC=∠CDB
(2)CA·BD=CB·AB
课后思考?
类比的方法应在经验科学中占很高的地位,而且科学家也曾按照这种推论方法获得很重要的结果。
——黑格尔
(1770—1831)德国著名哲学家
24.3相似三角形
——2.相似三角形的判定(2)
问题1:相似三角形的有关概念
(1). 三个角对应_____ 、三条边对应_______的两个三角形叫做相似三角形
(2).相似三角形的对应角 _____,对应边________ .
(3).相似比等于____的两个三角形全等.
问题2:我们已经有哪些判别两三角形相似的方法?
(1)相似三角形的定义
(2)两角对应相等的两个三角形相似。
相等
成比例
相等
成比例
1
一、复习提问,类比猜想
一、复习提问,类比猜想
问题3 :全等三角形有哪些判定方法
ASA ( AAS) SAS SSS
问题4:类比三角形全等的判定,你认为可能还有哪些方法能判定两个三角形相似 (请同桌讨论,大胆猜想)
猜想二:三边对应成比例的两个三角形相似
猜想一:两边对应成比例且夹角相等的两个三 角形相似
二、设计方案,验证结论
猜想二:
三边对应相等的两个三角形相似
猜想一:
两边对应成比例且夹角相等的两个三角形相似
1 、请分组设计猜想一或猜想二的验证方案
三角形相似的判定方法2:
两边对应成比例且夹角相等的两个
三角形相似
A
B
C
在△ ABC与△DEF中
∵ ∠B=∠E,
D
E
F
∴ △ ABC∽ △ DEF
(两边对应成比例且夹角相等的两个三角形相似)
上述判定方法中的“角”一定只能是两对应边的夹角吗?
我爱思考
想一想:在上述问题中如果这个角是这两条边中其中一条边的对角呢,两个三角形还一定相似吗?(小组内交流)
G
3.2
C
3.2
50°
)
4
A
B
2
1.6
50°
)
E
D
F
两边对应成比例且一边的对角对应相等的两三角形不一定相似
C
A
B
C'
A'
B'
三边对应成比例的两个三角形相似
三角形相似的判定方法3:
如图,在△ ABC与△ A′B′C′中,
∴ △ ABC∽ △ A′B′C′
(三边对应成比例的两个三角形相似.)
∵
二、归纳概括,得出结论
方法4: 三边对应成比例的两个三角形相似
方法3: 两边对应成比例且夹角相等的两
个三角形相似
我们已经有哪些判别两三角形相似的方法?
方法1: 相似三角形的定义
方法2: 两角对应相等的两个三角形相似。
已知,如图,要使△ABC∽△ACD,需要添加几个条件?是 ( )
已知,如图,要使△ABE∽△ACD,需要添加几个条件?是( )
例3 证明:图中△AEB和△FEC相似.
证明 ∵
,
∴
∴ △AEB∽△FEC(如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似).
∵ ∠AEB=∠FEC,
依据下列各组条件,证明△ABC和△A’B’C’相似
∠A=40° , AB=8, AC=15,
∠A’=40 °,A’B’=16,A’C’=30.
三.应用新知,解决问题
证明:
∴ △ACD∽△ABC(两边对应成比例且夹角相等的两个三角形相似).
如图,D在△ABC的AB边上AD=1,BD=2,
AC= .问:△ACD与△ABC相似吗?为什么?
A
B
C
D
答: △ACD∽△ABC
例4 在△ABC和△A′B′C′中,已知: AB=6cm,BC=8cm,AC=10cm,A′B′=18cm,B′C′=24cm,A′C′=30cm.试证明△ABC与△A′B′C′相似.
证明 ∵
,
∴
∴ △ABC∽△A′B′C′(三边对应成比例的两个三角形相似).
依据下列各组条件,证明△ABC和△A′B′C′相似
AB=10cm,BC=8cm,AC=16cm,
A′B′=16cm,B′C′=12.8cm,A′C ′=25.6cm
例6. 如图,在矩形ABCD中,AB=8,AD=4,在AB上取一点M,使AM=2,连接DM交AC于N.
(1)图中DM与AC具备怎样的位置关系?试说明理由。
(2)写出和△ADC相似的三角形(除△ABC外)。
答:(1)DM⊥AC
证明:∵在矩形ABCD中,
∠DAM= ∠CDA=90°,
DC=AB=8,
,
A
B
C
D
M
N
∴
∴△CDA∽ △DAM
∴∠1=∠2
∵∠2+∠3=90°
∴∠1+∠3=90°
∴DM⊥AC
(2)和△ADC相似的三角形有:
△MAD, △MNA, △AND, △DNC
8
4
2
4
8
1
2
3
∴∠AND=90°
下面图中的两个三角形是否相似? 请说说你的理由:
C
A
4
5
5
E
F
B
4
四.巩固新知,熟能生巧
如图,△ ABC与△ A′B′C′相似吗
你用什么方法来支持你的判断
∴△ ABC∽△ A′B′C′
(三边对应成比例的两个三角形相似.)
C
B
A
A′
B′
C′
解:如图,设小正方形的边长为1,由勾股定理可得:
答:这两个三角形相似。
你还有不同的证法吗?
五、积累总结,知识升华
方法3: 三边对应相等的两个三角形相似
方法2: 两边对应成比例且夹角相等的两个三角形相 似
1、三角形相似的判定方法有哪些?
(定义法: 对应角相等,对应边成比例的两个三角形相似)
方法1: 两角对应相等的两个三角形相似。
六、积累总结,知识升华
2、三角形全等、相似常用判别方法的比较:
三角形全等的判别 三角形相似的判别
ASA(AAS) 两角对应相等
SSS 三边对应成比例
SAS 两边对应成比例且夹角相等
六、积累总结,知识升华
2、在应用三角形相似的判定方法2时要注意什么问题?
3、通过本节课的学习你体会到了哪些重要的数学思想?
从特殊到一般、类比
必须是两边的夹角,而非对角
如图,△ABC中,AB=4,AC=6,点D是AB边上一点,且AD=2,在AC边上找一点E,使得以A、D、E为顶点的三角形与△ABC相似。并求出AE的长度。
A
B
C
D
E1
E2
AE的长度为3或4/3
有一池塘, 周围都是空地. 如果要测量池塘两端A、B间的距离, 你能利用本节课所学的知识解决这个问题吗
A
B
D
E
C
生活中的应用)
C
E
D
B
A
若:
试说明 :
(1)∠ABC=∠CDB
(2)CA·BD=CB·AB
课后思考?
