湘教版数学八年级上册 复习课件:2.5《全等三角形性质与判定》(共10张PPT)
文档属性
| 名称 | 湘教版数学八年级上册 复习课件:2.5《全等三角形性质与判定》(共10张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-13 17:18:50 | ||
图片预览

文档简介
(共10张PPT)
全等三角形的性质与判断
整理巩固下列基础知识方法
1.全等三角形的性质:
①__________________________;
②___________________________.
全等三角形的对应边相等
全等三角形的对应角相等
2.判定两个三角形全等的方法有:
_____________________________________
SAS
ASA
AAS
SSS
3.如何找判定三角形全等的条件?
①___________________________________
②___________________________________
根据已知条件找:由已知条件可得到什么
根据图形找:公共角,公共边,对顶角
整理巩固下列基础知识方法
4.通过判定三角形全等能解决哪些问题?
证明线段(或角相等)
证明线段(或角)所在的两个三角形全等.
转化
注意:
在转化过程中,有时需要添加辅助线.
A
B
C
D
2
3
4
1
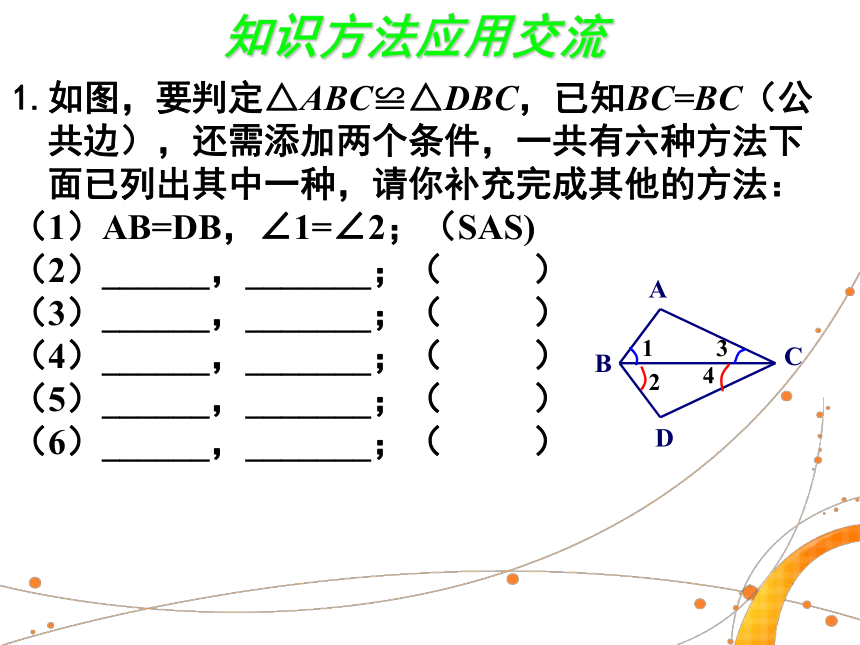
知识方法应用交流
1.如图,要判定△ABC≌△DBC,已知BC=BC(公
共边),还需添加两个条件,一共有六种方法下
面已列出其中一种,请你补充完成其他的方法:
(1)AB=DB,∠1=∠2;(SAS)
(2)______,_______;( )
(3)______,_______;( )
(4)______,_______;( )
(5)______,_______;( )
(6)______,_______;( )
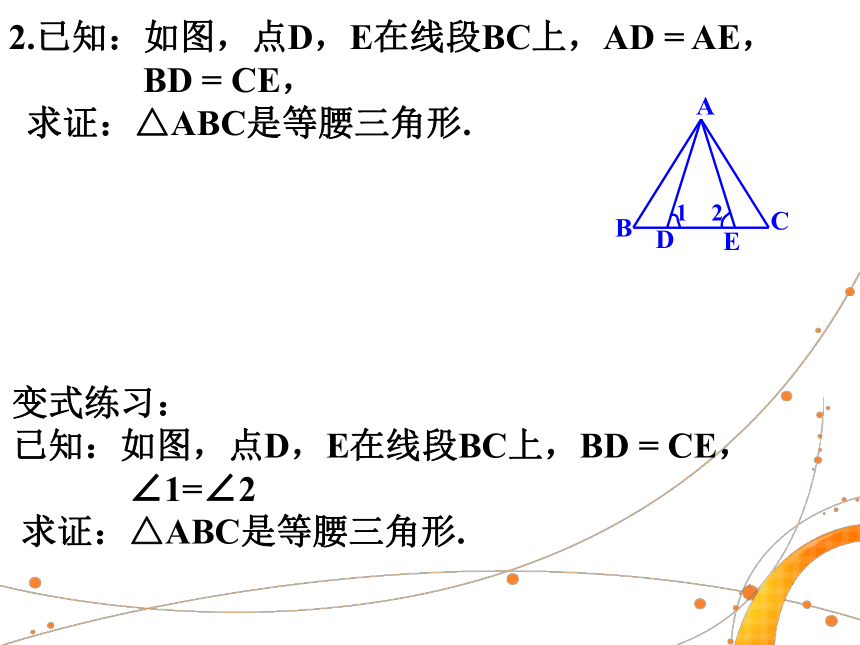
2.已知:如图,点D,E在线段BC上,AD = AE,
BD = CE,
求证:△ABC是等腰三角形.
1
2
A
B
C
D
E
变式练习:
已知:如图,点D,E在线段BC上,BD = CE,
∠1=∠2
求证:△ABC是等腰三角形.
3.如图,P是∠AOB的平分线OM上任意一点,
PE⊥OA于E,PF⊥OB于F,连EF.
求证:OP垂直平分EF .
A
O
B
M
P
E
F
4.如图,AC=BD,AB=DC,
求证:∠B=∠C.
A
B
C
D
E
1.已知:在△ABC中,AC=BC,∠ACB=900,点D是
AB的中点,点E是AB边上一点.
A
B
C
D
E
F
G
(1)
A
B
C
D
E
H
M
(2)
(2)直线AH垂直CE,垂足为H,交CD的延长线于点M
(如图②),找出图中与BE相等的线段,并证明.
(1) 直线BF垂直于CE于点F,交CD于点G(如图①),
求证:AE=CG;
思维拓展,举一反三
2.已知:如图,△ABC为正三角形,D是BC延长线
上一点,连结AD,以AD为边作等边三角形ADE,
连结CE,用你学过的知识探索AC、CD、CE三条
线段的长度有何关系 试写出探求过程.
A
B
C
D
E
作业布置
课本课后习题
全等三角形的性质与判断
整理巩固下列基础知识方法
1.全等三角形的性质:
①__________________________;
②___________________________.
全等三角形的对应边相等
全等三角形的对应角相等
2.判定两个三角形全等的方法有:
_____________________________________
SAS
ASA
AAS
SSS
3.如何找判定三角形全等的条件?
①___________________________________
②___________________________________
根据已知条件找:由已知条件可得到什么
根据图形找:公共角,公共边,对顶角
整理巩固下列基础知识方法
4.通过判定三角形全等能解决哪些问题?
证明线段(或角相等)
证明线段(或角)所在的两个三角形全等.
转化
注意:
在转化过程中,有时需要添加辅助线.
A
B
C
D
2
3
4
1
知识方法应用交流
1.如图,要判定△ABC≌△DBC,已知BC=BC(公
共边),还需添加两个条件,一共有六种方法下
面已列出其中一种,请你补充完成其他的方法:
(1)AB=DB,∠1=∠2;(SAS)
(2)______,_______;( )
(3)______,_______;( )
(4)______,_______;( )
(5)______,_______;( )
(6)______,_______;( )
2.已知:如图,点D,E在线段BC上,AD = AE,
BD = CE,
求证:△ABC是等腰三角形.
1
2
A
B
C
D
E
变式练习:
已知:如图,点D,E在线段BC上,BD = CE,
∠1=∠2
求证:△ABC是等腰三角形.
3.如图,P是∠AOB的平分线OM上任意一点,
PE⊥OA于E,PF⊥OB于F,连EF.
求证:OP垂直平分EF .
A
O
B
M
P
E
F
4.如图,AC=BD,AB=DC,
求证:∠B=∠C.
A
B
C
D
E
1.已知:在△ABC中,AC=BC,∠ACB=900,点D是
AB的中点,点E是AB边上一点.
A
B
C
D
E
F
G
(1)
A
B
C
D
E
H
M
(2)
(2)直线AH垂直CE,垂足为H,交CD的延长线于点M
(如图②),找出图中与BE相等的线段,并证明.
(1) 直线BF垂直于CE于点F,交CD于点G(如图①),
求证:AE=CG;
思维拓展,举一反三
2.已知:如图,△ABC为正三角形,D是BC延长线
上一点,连结AD,以AD为边作等边三角形ADE,
连结CE,用你学过的知识探索AC、CD、CE三条
线段的长度有何关系 试写出探求过程.
A
B
C
D
E
作业布置
课本课后习题
同课章节目录
