5.2.2 平行线的判定 教案 (表格式)人教版数学七年级下册
文档属性
| 名称 | 5.2.2 平行线的判定 教案 (表格式)人教版数学七年级下册 |

|
|
| 格式 | doc | ||
| 文件大小 | 464.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-09 09:35:13 | ||
图片预览


文档简介
课 题 5.2.2平行线的判定
授课教师 单位
教材版本 人教版 课型 新授课
教学目标 (一)知识与技能:1、能根据“同位角相等,两直线平行”证明“内错角相等,两直线平行”“同旁内角互补,两直线平行”,并能简单地应用这些结论; 2、初步了解证明的基本步骤和书写格式;3、体会几何中推理的严谨性、书写的规范性,发展初步的演绎推理能力.(二)数学思考通过“转化”数学思想的应用,让学生认识事物之间的普遍联系,相互转化的辩证唯物主义思想.(三)问题解决运用三种判定方法解决数学问题及实际问题.(四)情感态度1、通过学生体验、猜想并证明,让学生体会数学充满着探索和创造,培养学生团结协作、勇于创新的精神;2、在问题探索中体验成功的喜悦,增强学好数学的自信心.
教学重点 两种直线平行的三种判定方法、判定推论以及简单应用.
教学难点 如何用数学语言表达简单的推理过程.
教学方法 引导发现法、合作交流法、启发探究法.
教学过程
教学环节 教学活动设计 设计意图
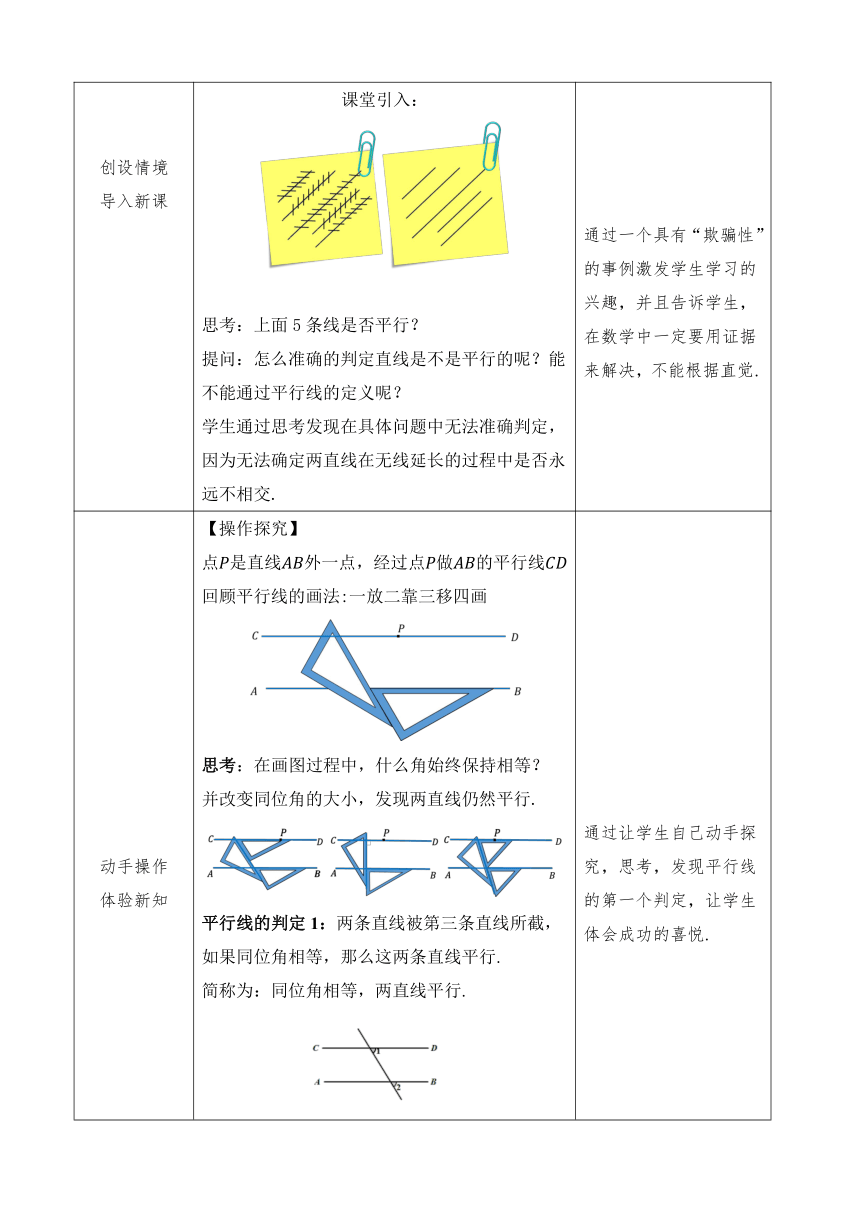
创设情境导入新课 课堂引入:思考:上面5条线是否平行?提问:怎么准确的判定直线是不是平行的呢?能不能通过平行线的定义呢?学生通过思考发现在具体问题中无法准确判定,因为无法确定两直线在无线延长的过程中是否永远不相交. 通过一个具有“欺骗性”的事例激发学生学习的兴趣,并且告诉学生,在数学中一定要用证据来解决,不能根据直觉.
动手操作体验新知 【操作探究】点 是直线 外一点,经过点 做 的平行线 回顾平行线的画法:一放二靠三移四画思考:在画图过程中,什么角始终保持相等?并改变同位角的大小,发现两直线仍然平行.平行线的判定1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简称为:同位角相等,两直线平行.数学语言:∵∠1=∠2(已知),∴ ∥ (同位角相等,两直线平行).【讨论探究】内错角或同旁内角能不能判定两直线平行?如果可以需要满足怎样的数量关系?探究一利用内错角来判断两条直线平行(学生小组讨论,师生合作完成利用内错角相等,判定两直线平行的说明方法)如图,∠1=∠3,直线 和直线 平行吗?请说明理由.解:平行,理由如下∵ ∠1=∠3(已知),∠3=∠2(对顶角相等),∴ ∠1=∠2(等量代换).∴ ∥ (同位角相等,两直线平行).平行线的判定2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简称为:内错角相等,两直线平行.数学语言:∵∠1=∠3(已知),∴ ∥ (内错角相等,两直线平行).探究二利用同旁内角互补来判定两条直线平行(学生小组讨论,学生自己完成利用同旁内角互补,判定两直线平行的说明方法).如图,∠1+∠2=180°,直线 和直线 平行吗?请说明理由.解:平行,理由如下:∵ ∠1+∠2=180°(已知),∠3+∠2=180°(邻补角的性质),∴ ∠1=∠3(等量代换).∴ ∥ (同位角相等,两直线平行).平行线的判定3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简称为:同旁内角互补,两直线平行.数学语言:∵∠1+∠4=180°(已知),∴ ∥ (同旁内角互补,两直线平行).练习1如图, 是 上一点, 是 上一点, 是 延长线上一点,(1)如果∠ =∠ ,可以判断哪两条线平行?为什么?(2)如果∠ =∠ ,可以判断哪两条线平行?为什么?(3)如果∠ +∠ =180°,可以判断哪两条线平行?为什么?(1) ∥ 同位角相等,两直线平行.(2) ∥ 内错角相等,两直线平行.(3) ∥ 同旁内角互补,两直线平行. 通过让学生自己动手探究,思考,发现平行线的第一个判定,让学生体会成功的喜悦.通过简单的例题应用,巩固所学新知,加深学生记忆.两个探究都是由未知转化成已知来解决.【探究1】师生合作共同完成,旨在再次规范学生的做题步骤.【探究2】由学生独立完成,旨在检测学生的知识迁移能力,以及步骤的规范化程度.由同位角开始,循序渐进地探讨平行线的判定方法,清晰明了,并在此过程中训练学生的推理能力、逻辑思维能力.
巩固新知学以致用 【解决问题】在同一平面内,直线 、 均与直线 垂直, 、 为垂足,试判断 与 是否平行?(可尝试多种方法 ).解:∵ ⊥ , ⊥ ,∴∠ =∠ =90°(垂直的性质).∴ ∥ (同位角相等,两直线平行).平行线判定的推论:在同一平面内,垂直于同一条直线的两条直线平行.(利用教具解释为什么在同一平面内).练习2若∠1=∠4, ∠1+∠2=180°,则直线 , , 的位置关系如何?解:∵ ∠1=∠4(已知),∴_________(______________________).∵ ∠1+∠2=180°(已知),∠3+∠2=180°(____________),∴ ∠1=∠3(_________).∴________(______________________).∴ ∥ ∥ (平行公理的推论).练习3如图,当∠1=∠3时,直线 和 平行吗?为什么?解:平行. 理由如下:∵∠1=∠ (对顶角相等),∠1=∠3(已知),∴∠ =∠3(等量代换).∴ ∥ (同位角相等两直线平行).练习4如图,当 ⊥ , ⊥ 且∠1=∠2,试说明 ∥ 解:∵ ⊥ , ⊥ ,∴∠ =∠ =90°.∵∠1=∠2(已知),∴∠ ∠1=∠ ∠2.∴∠ =∠ .∴ ∥ (内错角相等,两直线平行). 通过例题,可以巩固所学新知,同时培养学生灵活运用平行线的判定方法解决问题的能力.通过练习题,及时反馈学生的学习情况,以便查漏补缺,进一步提升教学效果.
课堂小结 平行线的三种判定方法:同位角相等,两直线平行.内错角相等,两直线平行.同旁内角互补,两直线平行.平行线判定的推论:在同一平面内,垂直于同一条直线的两条直线平行. 引导学生对本节课知识进行梳理总结,明确重点.
布置作业 课时作业
板书设计 一、平行线的三种判定方法和判定推论.二、练习3的板书.三、学生习题版书展示. 将本节重要知识呈现在学生面前,让学生更进一步理解.
授课教师 单位
教材版本 人教版 课型 新授课
教学目标 (一)知识与技能:1、能根据“同位角相等,两直线平行”证明“内错角相等,两直线平行”“同旁内角互补,两直线平行”,并能简单地应用这些结论; 2、初步了解证明的基本步骤和书写格式;3、体会几何中推理的严谨性、书写的规范性,发展初步的演绎推理能力.(二)数学思考通过“转化”数学思想的应用,让学生认识事物之间的普遍联系,相互转化的辩证唯物主义思想.(三)问题解决运用三种判定方法解决数学问题及实际问题.(四)情感态度1、通过学生体验、猜想并证明,让学生体会数学充满着探索和创造,培养学生团结协作、勇于创新的精神;2、在问题探索中体验成功的喜悦,增强学好数学的自信心.
教学重点 两种直线平行的三种判定方法、判定推论以及简单应用.
教学难点 如何用数学语言表达简单的推理过程.
教学方法 引导发现法、合作交流法、启发探究法.
教学过程
教学环节 教学活动设计 设计意图
创设情境导入新课 课堂引入:思考:上面5条线是否平行?提问:怎么准确的判定直线是不是平行的呢?能不能通过平行线的定义呢?学生通过思考发现在具体问题中无法准确判定,因为无法确定两直线在无线延长的过程中是否永远不相交. 通过一个具有“欺骗性”的事例激发学生学习的兴趣,并且告诉学生,在数学中一定要用证据来解决,不能根据直觉.
动手操作体验新知 【操作探究】点 是直线 外一点,经过点 做 的平行线 回顾平行线的画法:一放二靠三移四画思考:在画图过程中,什么角始终保持相等?并改变同位角的大小,发现两直线仍然平行.平行线的判定1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简称为:同位角相等,两直线平行.数学语言:∵∠1=∠2(已知),∴ ∥ (同位角相等,两直线平行).【讨论探究】内错角或同旁内角能不能判定两直线平行?如果可以需要满足怎样的数量关系?探究一利用内错角来判断两条直线平行(学生小组讨论,师生合作完成利用内错角相等,判定两直线平行的说明方法)如图,∠1=∠3,直线 和直线 平行吗?请说明理由.解:平行,理由如下∵ ∠1=∠3(已知),∠3=∠2(对顶角相等),∴ ∠1=∠2(等量代换).∴ ∥ (同位角相等,两直线平行).平行线的判定2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简称为:内错角相等,两直线平行.数学语言:∵∠1=∠3(已知),∴ ∥ (内错角相等,两直线平行).探究二利用同旁内角互补来判定两条直线平行(学生小组讨论,学生自己完成利用同旁内角互补,判定两直线平行的说明方法).如图,∠1+∠2=180°,直线 和直线 平行吗?请说明理由.解:平行,理由如下:∵ ∠1+∠2=180°(已知),∠3+∠2=180°(邻补角的性质),∴ ∠1=∠3(等量代换).∴ ∥ (同位角相等,两直线平行).平行线的判定3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简称为:同旁内角互补,两直线平行.数学语言:∵∠1+∠4=180°(已知),∴ ∥ (同旁内角互补,两直线平行).练习1如图, 是 上一点, 是 上一点, 是 延长线上一点,(1)如果∠ =∠ ,可以判断哪两条线平行?为什么?(2)如果∠ =∠ ,可以判断哪两条线平行?为什么?(3)如果∠ +∠ =180°,可以判断哪两条线平行?为什么?(1) ∥ 同位角相等,两直线平行.(2) ∥ 内错角相等,两直线平行.(3) ∥ 同旁内角互补,两直线平行. 通过让学生自己动手探究,思考,发现平行线的第一个判定,让学生体会成功的喜悦.通过简单的例题应用,巩固所学新知,加深学生记忆.两个探究都是由未知转化成已知来解决.【探究1】师生合作共同完成,旨在再次规范学生的做题步骤.【探究2】由学生独立完成,旨在检测学生的知识迁移能力,以及步骤的规范化程度.由同位角开始,循序渐进地探讨平行线的判定方法,清晰明了,并在此过程中训练学生的推理能力、逻辑思维能力.
巩固新知学以致用 【解决问题】在同一平面内,直线 、 均与直线 垂直, 、 为垂足,试判断 与 是否平行?(可尝试多种方法 ).解:∵ ⊥ , ⊥ ,∴∠ =∠ =90°(垂直的性质).∴ ∥ (同位角相等,两直线平行).平行线判定的推论:在同一平面内,垂直于同一条直线的两条直线平行.(利用教具解释为什么在同一平面内).练习2若∠1=∠4, ∠1+∠2=180°,则直线 , , 的位置关系如何?解:∵ ∠1=∠4(已知),∴_________(______________________).∵ ∠1+∠2=180°(已知),∠3+∠2=180°(____________),∴ ∠1=∠3(_________).∴________(______________________).∴ ∥ ∥ (平行公理的推论).练习3如图,当∠1=∠3时,直线 和 平行吗?为什么?解:平行. 理由如下:∵∠1=∠ (对顶角相等),∠1=∠3(已知),∴∠ =∠3(等量代换).∴ ∥ (同位角相等两直线平行).练习4如图,当 ⊥ , ⊥ 且∠1=∠2,试说明 ∥ 解:∵ ⊥ , ⊥ ,∴∠ =∠ =90°.∵∠1=∠2(已知),∴∠ ∠1=∠ ∠2.∴∠ =∠ .∴ ∥ (内错角相等,两直线平行). 通过例题,可以巩固所学新知,同时培养学生灵活运用平行线的判定方法解决问题的能力.通过练习题,及时反馈学生的学习情况,以便查漏补缺,进一步提升教学效果.
课堂小结 平行线的三种判定方法:同位角相等,两直线平行.内错角相等,两直线平行.同旁内角互补,两直线平行.平行线判定的推论:在同一平面内,垂直于同一条直线的两条直线平行. 引导学生对本节课知识进行梳理总结,明确重点.
布置作业 课时作业
板书设计 一、平行线的三种判定方法和判定推论.二、练习3的板书.三、学生习题版书展示. 将本节重要知识呈现在学生面前,让学生更进一步理解.
