2023-2024学年度第二学期北师大版六年级数学期末检测(含答案)
文档属性
| 名称 | 2023-2024学年度第二学期北师大版六年级数学期末检测(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-10 21:00:30 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2023-2024学年度第二学期北师大版六年级数学期末检测
一、单选题(共5分)
1. 一个圆柱和一个圆锥,底面周长的比是2:3,体积比是5:6,那么这个圆柱和圆锥的高的最简整数比是( )。
A.5:8 B.12:5 C.8:5 D.5:12
2.将下边的图形按1∶2的比缩小后的图形是( )。
A. B. C.
3.将一个图形平移后得到的图形和原图相比,面积比是( )。
A.1∶2 B.1∶4 C.1∶1
4.冰雕艺术家有时会通过人工制作特色形状的冰块来进行冰雕雕刻。一位冰雕艺术家将相同质量的水倒入大小不同的圆柱形水桶中,在一定条件下凝固成冰。则形成的冰的底面积和高( )。
A.成正比例 B.成反比例 C.不成比例
5.步测一段路,平均步长和所走的步数( )。
A.成反比例 B.成正比例 C.不成比例
二、判断题(共5分)
6.小红有10本练习本,用完的本数与剩下的本数成反比例。 ( )
7.一个圆绕圆心不管旋转多少度都能与原图形重合。 ( )
8.一个正方形按1:3 缩小后,它的周长和面积都缩小了3倍。 ( )
9. 比例尺的前项都比后项小。 ( )
10.一个圆柱的底面周长和高相等,那么它的侧面沿高展开一定是正方形。 ( )
三、填空题(共22分)
11.如图,把一个高6厘米的圆柱体平均分成若干份,拼成一个近似的长方体,这个长方体的表面积比原来增加了36cm2,则这个圆柱体的侧面积是
cm2,和它等底等高的圆锥体的体积是 cm3。
12.两个底面积相等的圆柱,一个圆柱的高为4d m,体积为 ,另一个圆柱的高为8dm,体积为 dm 。
13.一个圆锥形容器里盛满水,水面高60厘米,将水倒入和它等底等高的圆柱形容器中,水的高度是 厘米。
14.在一幅比例尺是1:300的图纸上,量得一个圆形花坛的直径是2cm。这个花坛的实际占地面积是 m2。如果沿着这个花坛的四周修一条宽1m的环形小路,那么小路的面积是 m 。
15.淘淘来到实验楼,看到一楼大厅中的校园沙盘后驻足观赏,发现标注沙盘的比例尺是1∶240,而且在沙盘上校门到主楼大约是45 cm,那么淘淘进校门后大约要走 m才能进入主楼。
16.汽车厂生产一批汽车模型,模型长度与该款汽车实际长度的比是1∶14,量得模型的长度是35厘米,汽车的实际长度是 米。
17.描述一个图形旋转的过程,首先要确定 的位置,并按图形旋转时绕 旋转的 ,旋转的 来描述。
18.如下图,指针从“12”绕点O顺时针旋转90°到“ ”,指针从“12”绕点O顺时针旋转 °到“2”,指针从“12”绕点O逆时针旋转180°到“ ”。
19.若5x=8y(x、y都不为0),则x和y成 比例;若=,则x和y成 比例。
20.一个自然数(0除外)和它的倒数成 比例,一个圆的周长和直径成 比例。
21.如下图,x与y是两个相关联的量。当x=2时,y= ;当y=40时,x= 。x和y成 比例。
四、计算题(共18分)
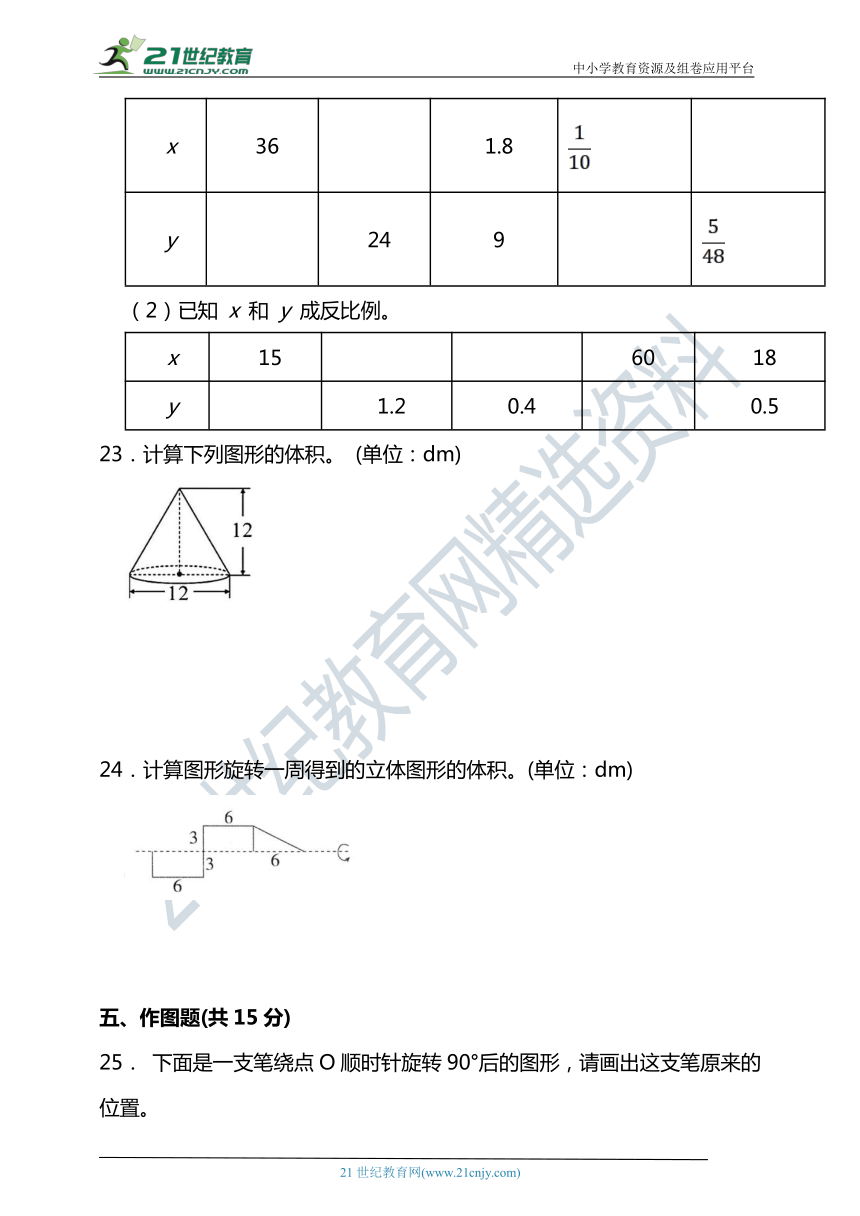
22.填表。
(1)已知 x 和 y 成正比例。
x 36 1.8
y 24 9
(2)已知 x 和 y 成反比例。
x 15 60 18
y 1.2 0.4 0.5
23.计算下列图形的体积。 (单位:dm)
24.计算图形旋转一周得到的立体图形的体积。(单位:dm)
五、作图题(共15分)
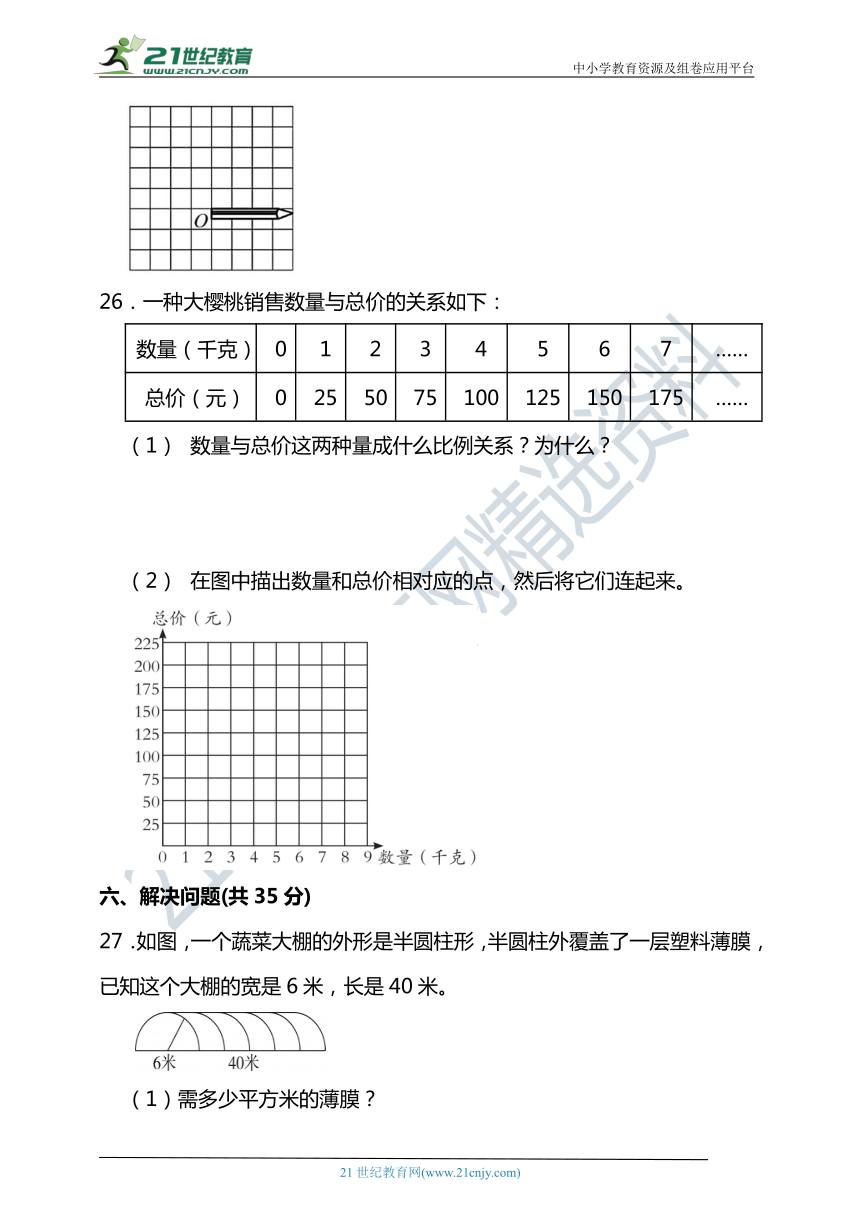
25. 下面是一支笔绕点O顺时针旋转90°后的图形,请画出这支笔原来的位置。
26.一种大樱桃销售数量与总价的关系如下:
数量(千克) 0 1 2 3 4 5 6 7 ……
总价(元) 0 25 50 75 100 125 150 175 ……
(1) 数量与总价这两种量成什么比例关系?为什么?
(2) 在图中描出数量和总价相对应的点,然后将它们连起来。
六、解决问题(共35分)
27.如图,一个蔬菜大棚的外形是半圆柱形,半圆柱外覆盖了一层塑料薄膜,已知这个大棚的宽是6米,长是40米。
(1)需多少平方米的薄膜?
(2)整个大棚的空间是多少立方米?
28.你知道吗?儿童体内水分和体重的比约是7:10,淘气的体重为45千克,他体内的水分大约是多少千克?(用比例的方法解答)
29.工程队修建一段高速公路,原计划每天修0.4千米,60天完成任务。由于增加了机器设备,实际每天比原计划多修25%,实际多少天完成任务?(用比例解)
30.一辆汽车的行驶路程和耗油量情况如下表。
行驶路程/千米 15 45 75 90 150
耗油量/升 2 6 10 12 20
(1) 汽车行驶路程和耗油量成什么比例?为什么?
(2)这辆汽车从A地开往B地,出发时油箱里有油50升,达到B地时
剩下34升,从A地到B地有多少千米?
31.某工程队铺设一段下水道,原计划每天铺设20米,15天完成。实际每天多了5米,实际多少天完成了任务?(用比例解)
答案
1.A
2.C
3.C
4.B
5.A
6.×
7.√
8.×
9.×
10.√
11.113.04;56.52
12.160
13.20
14.28.26;1.98
15.108
16.4.9
17.图形旋转后;旋转中心;方向;角度
18.3;60;6
19.正;正
20.反;正
21.16;5;正
22.(1)
x 36 4.8 1.8
y 180 24 9
(2)
x 15 7.5 22.5 60 18
y 0.6 1.2 0.4 0.15 0.5
23.解:3.14×(12÷2)2×12×
=3.14×36×4
=113.04×4
=452.16(dm3)
24.解:旋转一周得到的立体图形是圆柱+圆柱+圆锥,
3.14×32×6+3.14×32×6+3.14×32×6×
=169.56+169.56+56.52
= 395.64(dm3)
答:立体图形的体积是395.64立方分米。
25.解:
26.(1)解:成正比例关系,因为它们的比值一定。
(2)解:
27.(1)解:3.14×6÷2×40
=9.42×40
=376.8(平方米)
答:需376.8平方米的薄膜。
(2)解:3.14×(6÷2)2×40÷2
=3.14×9×40÷2
=28.26×40÷2
=1130.4÷2
=565.2(立方米)
答:整个大棚的空间是565.2立方米。
28.解:设他体内的水分大约是x千克。
x:45=7:10
10x=45×7
10x=315
x=315÷10
x=31.5
答:他体内的水分大约是31.5千克。
29.解:设实际x天完成任务。
0.4×(1+25%)x=0.4×60
0.4×1.25×x=24
0.5x=24
x=24÷0.5
x=48
答:实际48天完成任务。
30.(1)解:汽车行驶路程和耗油量成正比例;因为耗油量越大,行驶路程越远。
(2)解:50-34=16(升)
16×(75÷10)=120(千米)
答:从A地到B地有120千米。
31.解:设实际x天完成了任务
(20+5)x=20×15
25x=300
x=12
答:实际12天完成任务。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2023-2024学年度第二学期北师大版六年级数学期末检测
一、单选题(共5分)
1. 一个圆柱和一个圆锥,底面周长的比是2:3,体积比是5:6,那么这个圆柱和圆锥的高的最简整数比是( )。
A.5:8 B.12:5 C.8:5 D.5:12
2.将下边的图形按1∶2的比缩小后的图形是( )。
A. B. C.
3.将一个图形平移后得到的图形和原图相比,面积比是( )。
A.1∶2 B.1∶4 C.1∶1
4.冰雕艺术家有时会通过人工制作特色形状的冰块来进行冰雕雕刻。一位冰雕艺术家将相同质量的水倒入大小不同的圆柱形水桶中,在一定条件下凝固成冰。则形成的冰的底面积和高( )。
A.成正比例 B.成反比例 C.不成比例
5.步测一段路,平均步长和所走的步数( )。
A.成反比例 B.成正比例 C.不成比例
二、判断题(共5分)
6.小红有10本练习本,用完的本数与剩下的本数成反比例。 ( )
7.一个圆绕圆心不管旋转多少度都能与原图形重合。 ( )
8.一个正方形按1:3 缩小后,它的周长和面积都缩小了3倍。 ( )
9. 比例尺的前项都比后项小。 ( )
10.一个圆柱的底面周长和高相等,那么它的侧面沿高展开一定是正方形。 ( )
三、填空题(共22分)
11.如图,把一个高6厘米的圆柱体平均分成若干份,拼成一个近似的长方体,这个长方体的表面积比原来增加了36cm2,则这个圆柱体的侧面积是
cm2,和它等底等高的圆锥体的体积是 cm3。
12.两个底面积相等的圆柱,一个圆柱的高为4d m,体积为 ,另一个圆柱的高为8dm,体积为 dm 。
13.一个圆锥形容器里盛满水,水面高60厘米,将水倒入和它等底等高的圆柱形容器中,水的高度是 厘米。
14.在一幅比例尺是1:300的图纸上,量得一个圆形花坛的直径是2cm。这个花坛的实际占地面积是 m2。如果沿着这个花坛的四周修一条宽1m的环形小路,那么小路的面积是 m 。
15.淘淘来到实验楼,看到一楼大厅中的校园沙盘后驻足观赏,发现标注沙盘的比例尺是1∶240,而且在沙盘上校门到主楼大约是45 cm,那么淘淘进校门后大约要走 m才能进入主楼。
16.汽车厂生产一批汽车模型,模型长度与该款汽车实际长度的比是1∶14,量得模型的长度是35厘米,汽车的实际长度是 米。
17.描述一个图形旋转的过程,首先要确定 的位置,并按图形旋转时绕 旋转的 ,旋转的 来描述。
18.如下图,指针从“12”绕点O顺时针旋转90°到“ ”,指针从“12”绕点O顺时针旋转 °到“2”,指针从“12”绕点O逆时针旋转180°到“ ”。
19.若5x=8y(x、y都不为0),则x和y成 比例;若=,则x和y成 比例。
20.一个自然数(0除外)和它的倒数成 比例,一个圆的周长和直径成 比例。
21.如下图,x与y是两个相关联的量。当x=2时,y= ;当y=40时,x= 。x和y成 比例。
四、计算题(共18分)
22.填表。
(1)已知 x 和 y 成正比例。
x 36 1.8
y 24 9
(2)已知 x 和 y 成反比例。
x 15 60 18
y 1.2 0.4 0.5
23.计算下列图形的体积。 (单位:dm)
24.计算图形旋转一周得到的立体图形的体积。(单位:dm)
五、作图题(共15分)
25. 下面是一支笔绕点O顺时针旋转90°后的图形,请画出这支笔原来的位置。
26.一种大樱桃销售数量与总价的关系如下:
数量(千克) 0 1 2 3 4 5 6 7 ……
总价(元) 0 25 50 75 100 125 150 175 ……
(1) 数量与总价这两种量成什么比例关系?为什么?
(2) 在图中描出数量和总价相对应的点,然后将它们连起来。
六、解决问题(共35分)
27.如图,一个蔬菜大棚的外形是半圆柱形,半圆柱外覆盖了一层塑料薄膜,已知这个大棚的宽是6米,长是40米。
(1)需多少平方米的薄膜?
(2)整个大棚的空间是多少立方米?
28.你知道吗?儿童体内水分和体重的比约是7:10,淘气的体重为45千克,他体内的水分大约是多少千克?(用比例的方法解答)
29.工程队修建一段高速公路,原计划每天修0.4千米,60天完成任务。由于增加了机器设备,实际每天比原计划多修25%,实际多少天完成任务?(用比例解)
30.一辆汽车的行驶路程和耗油量情况如下表。
行驶路程/千米 15 45 75 90 150
耗油量/升 2 6 10 12 20
(1) 汽车行驶路程和耗油量成什么比例?为什么?
(2)这辆汽车从A地开往B地,出发时油箱里有油50升,达到B地时
剩下34升,从A地到B地有多少千米?
31.某工程队铺设一段下水道,原计划每天铺设20米,15天完成。实际每天多了5米,实际多少天完成了任务?(用比例解)
答案
1.A
2.C
3.C
4.B
5.A
6.×
7.√
8.×
9.×
10.√
11.113.04;56.52
12.160
13.20
14.28.26;1.98
15.108
16.4.9
17.图形旋转后;旋转中心;方向;角度
18.3;60;6
19.正;正
20.反;正
21.16;5;正
22.(1)
x 36 4.8 1.8
y 180 24 9
(2)
x 15 7.5 22.5 60 18
y 0.6 1.2 0.4 0.15 0.5
23.解:3.14×(12÷2)2×12×
=3.14×36×4
=113.04×4
=452.16(dm3)
24.解:旋转一周得到的立体图形是圆柱+圆柱+圆锥,
3.14×32×6+3.14×32×6+3.14×32×6×
=169.56+169.56+56.52
= 395.64(dm3)
答:立体图形的体积是395.64立方分米。
25.解:
26.(1)解:成正比例关系,因为它们的比值一定。
(2)解:
27.(1)解:3.14×6÷2×40
=9.42×40
=376.8(平方米)
答:需376.8平方米的薄膜。
(2)解:3.14×(6÷2)2×40÷2
=3.14×9×40÷2
=28.26×40÷2
=1130.4÷2
=565.2(立方米)
答:整个大棚的空间是565.2立方米。
28.解:设他体内的水分大约是x千克。
x:45=7:10
10x=45×7
10x=315
x=315÷10
x=31.5
答:他体内的水分大约是31.5千克。
29.解:设实际x天完成任务。
0.4×(1+25%)x=0.4×60
0.4×1.25×x=24
0.5x=24
x=24÷0.5
x=48
答:实际48天完成任务。
30.(1)解:汽车行驶路程和耗油量成正比例;因为耗油量越大,行驶路程越远。
(2)解:50-34=16(升)
16×(75÷10)=120(千米)
答:从A地到B地有120千米。
31.解:设实际x天完成了任务
(20+5)x=20×15
25x=300
x=12
答:实际12天完成任务。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
