2024年湖北省随县中考适应性考试数学试题(含答案)
文档属性
| 名称 | 2024年湖北省随县中考适应性考试数学试题(含答案) | 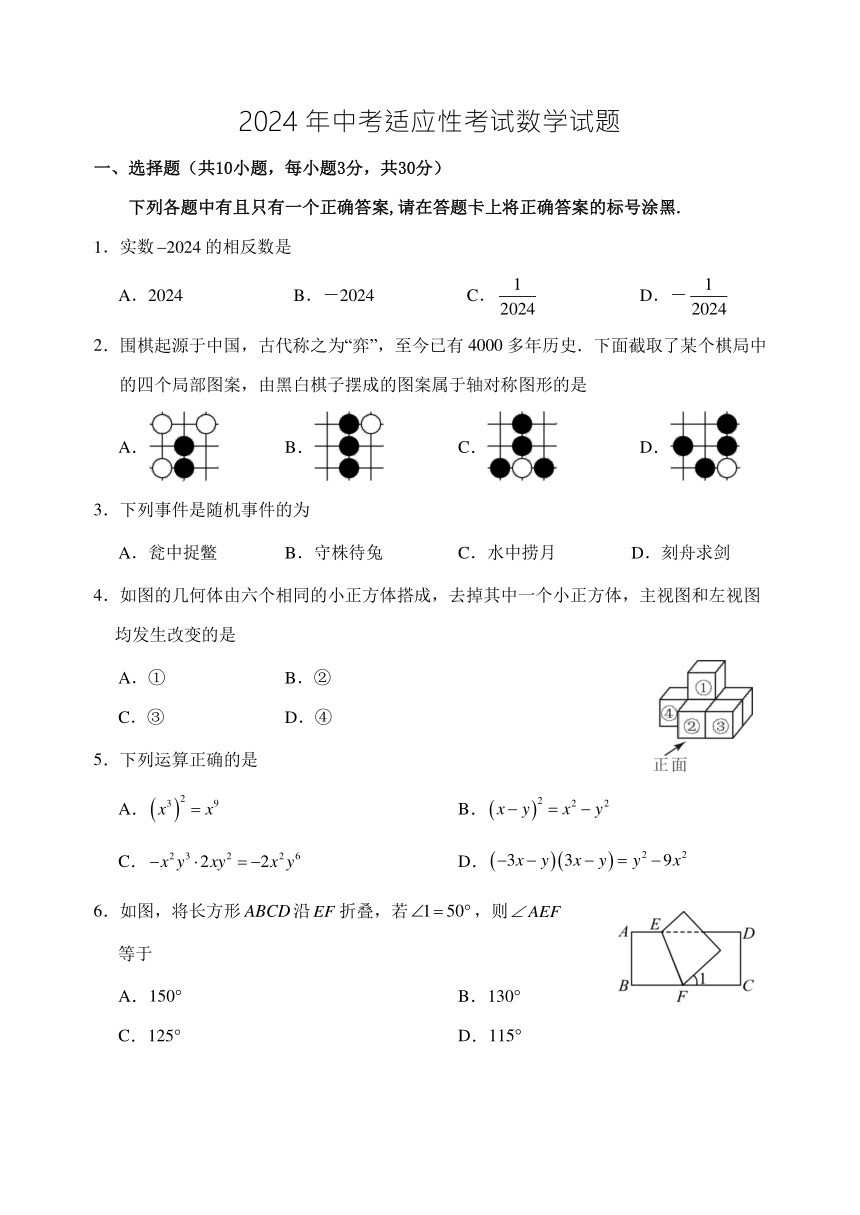 | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-09 13:50:58 | ||
图片预览





文档简介
2024年中考适应性考试数学试题
一、选择题(共10小题,每小题3分,共30分)
下列各题中有且只有一个正确答案,请在答题卡上将正确答案的标号涂黑.
1.实数的相反数是
A.2024 B.-2024 C. D.-
2.围棋起源于中国,古代称之为“弈”,至今已有4000多年历史.下面截取了某个棋局中的四个局部图案,由黑白棋子摆成的图案属于轴对称图形的是
A. B. C. D.
3.下列事件是随机事件的为
A.瓮中捉鳖 B.守株待兔 C.水中捞月 D.刻舟求剑
4.如图的几何体由六个相同的小正方体搭成,去掉其中一个小正方体,主视图和左视图均发生改变的是
A.① B.②
C.③ D.④
5.下列运算正确的是
A. B.
C. D.
6.如图,将长方形沿折叠,若,则
等于
A. B.
C. D.
7.通常情况下酚酞遇酸性和中性溶液不变色,遇碱性溶液变红色.一次化学课上,学生用酚酞溶液检测四瓶标签被污染无法分辨的无色溶液的酸碱性.已知四瓶溶液分别是A:盐酸(呈酸性),B:硝酸钾溶液(呈中性),C:氢氧化钠溶液(呈碱性),D:氢氧化钾溶液(呈碱性).小周将任选的两瓶溶液滴入酚酞溶液进行检测,则两瓶溶液恰好都变红色的概率是
A. B. C. D.
8.学校举行篮球比赛.图中的四个点分别描述了甲、乙、丙、丁四位同学投篮的命中率y(投进的次数占尝试投篮次数的百分率)与尝试投篮次数x的情况,其中所有投进的球记2分,描述乙、丁两位同学情况的点恰好在同一个反比例函数的图像上,则投篮得分最多的是
A.甲 B.乙 C.丙 D.丁
9.在边长为1的正五边形内,所有到点的距离大于且到点的距离小于1的点组成图形的面积是
A. B.
C. D.
10.下列不可能是函数图象的是
A B C D
二、填空题(共6小题,每小题3分,共18分)
下列各题不需要写出解答过程,请将结果直接填写在答题卡指定的位置.
11.2024年全国新注册登记的新能源汽车预计约有1335万辆,将数据1335万用科学记数法表示为 .
12.写出一个图象经过第一、二、四象限的一次函数解析式是 .
13.化简的结果是 .
14.2024年4月25日20时59分,运载火箭托举着神舟十八号载人飞船,在酒泉卫星发射中心点火升空,送航天员奔赴“天宫”.如图,神舟十八号载人飞船从地面O处成功发射,当飞船到达点A时,地面D处的雷达站测得AD=4000米,仰角为37°,0.3秒后,飞船直线上升到达点B处,此时地面C处的雷达站测得B处的仰角为45°,点O,C,D在同一直线上,已知C,D两处相距460米,则飞船从A到B处的平均速度为 米/秒.(结果精确到1米;参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
15.已知抛物线与轴的两交点的横坐标为m,n,满足. 下列结论:
①;
②若,当时,随的增大而减小;
③若有一个根是大于的负数,则;
④.
其中正确的结论是________.(填写序号)
如图,在中,分别是边上的点,且.
则的最大值是 .
三、解答题(共8小题,共72分)
下列各题需要在答题卡指定的位置写出文字说明、证明过程、演算步骤或画出图形.
17.(本小题满分8分)
求满足不等式组的整数解.
18.(本小题满分8分)
如图,在平行四边形中,点E,F,G,H分别在边AB,BC,CD,DA上,且.
(1)求证:≌;
(2)请添加一个条件,使四边形为矩形(不需说明理由).
19.(本小题满分8分)
为了解武汉市初中生每周锻炼身体的时长t(单位:小时)的情况,在武汉市随机抽取部分初中生进行调查,按五个组别:A组(3t<4),B组(4t<5),C组(5t<6),D组(6t<7),E组(7t<8)进行整理,绘制如下两幅不完整的统计图.
所抽取学生周锻炼时长的频数直方图 所抽取学生周锻炼时长的扇形统计图
(1)这次抽样调查的样本容量为______;
(2)抽取的样本中,每周锻炼身体时长的中位数落在______组,A组所在扇形的圆心角大小是______;
(3)若武汉市共有250000名初中生,请估计每周锻炼时间不低于6小时的学生人数.
20.(本小题满分8分)
如图,AC是⊙O的弦,OD AC,连接OA,OC,点B在⊙O外,AB=AC,连接BC交OD于E,交OA于F,.
(1)求证:AB是⊙O的切线;
(2)若,,求⊙O的半径.
21.(本小题满分8分)
如图是由小正方形组成的网格,每个小正方形的顶点叫做格点,A,B,C都是格点.仅用无刻度的直尺在给定网格中完成画图.
(1)先在上画点,使平分,再画的中点;
(2)先画点,使四边形为平行四边形,再将绕点旋转得,使得的对应点落在直线上.
22.(本小题满分10分)
乒乓球是我国国球.球台长为2.8m,中间处球网的高度为1.5dm.现有一台乒乓球发球器,球从发球器出口到第一次接触台面的运动轨迹近似为一条直线.从第一次接触台面到第二次接触台面的运动轨迹近似为一条抛物线.乒乓球第一次接触台面在球网左侧,越过球网(擦网不影响球运动轨迹)后,第二次接触台面在球网右侧为成功发球.乒乓球大小忽略不计.如图,当发球器放在球台左端时,通过测量得到球距离台面高度y(单位:dm)与球距离发球器出口的水平距离x(单位:dm)的相关数据,如下表所示:
x(dm) 0 2 4 6 8 10 12 14 …
y(dm) 3.36 2.52 1.68 0.84 0 1.40 2.40 3 …
(1)直接写出球从发球器出口到第一次接触台面时y关于x的函数解析式;(写出自变量的取值范围)
(2)求乒乓球第二次接触台面时与发球器出口的水平距离;
(3)发球器有一个滑轨,可以让发球口向右平移,若要成功发球,发球口最多向右平移多少dm?
23.(本小题满分10分)
问题提出:如图1,是正方形边上一点,延长至使,四边形是正方形,,连,探究与的数量关系.
问题探究:(1)先将问题特殊化,如图2,当与重合时,直接写出与的数量关系;
(2)再探究一般情形,如图1,求与的数量关系.
问题拓展:(3)如图3,是矩形边上一点,,在的延长线上且,,矩形满足,若,求与的数量关系.
图1 图2 图3
24.(本小题满分12分)
抛物线交轴于A,B两点(A在B的左边),交y轴于点C.
(1)如图1,当时,
①直接写出A,B,C三点的坐标;
②抛物线的顶点为D,求证:∠DAB=∠ACB;
(2)如图2,将抛物线平移得到抛物线,其顶点为原点.过点P(0,1)的直线与抛物线交于M,N两点.直线QM,QN与抛物线只有一个交点,连接PQ,若PQ MN恒成立,求a.
图1 图2
一、选择题(共10小题,每小题3分,共30分)
下列各题中有且只有一个正确答案,请在答题卡上将正确答案的标号涂黑.
1.实数的相反数是
A.2024 B.-2024 C. D.-
2.围棋起源于中国,古代称之为“弈”,至今已有4000多年历史.下面截取了某个棋局中的四个局部图案,由黑白棋子摆成的图案属于轴对称图形的是
A. B. C. D.
3.下列事件是随机事件的为
A.瓮中捉鳖 B.守株待兔 C.水中捞月 D.刻舟求剑
4.如图的几何体由六个相同的小正方体搭成,去掉其中一个小正方体,主视图和左视图均发生改变的是
A.① B.②
C.③ D.④
5.下列运算正确的是
A. B.
C. D.
6.如图,将长方形沿折叠,若,则
等于
A. B.
C. D.
7.通常情况下酚酞遇酸性和中性溶液不变色,遇碱性溶液变红色.一次化学课上,学生用酚酞溶液检测四瓶标签被污染无法分辨的无色溶液的酸碱性.已知四瓶溶液分别是A:盐酸(呈酸性),B:硝酸钾溶液(呈中性),C:氢氧化钠溶液(呈碱性),D:氢氧化钾溶液(呈碱性).小周将任选的两瓶溶液滴入酚酞溶液进行检测,则两瓶溶液恰好都变红色的概率是
A. B. C. D.
8.学校举行篮球比赛.图中的四个点分别描述了甲、乙、丙、丁四位同学投篮的命中率y(投进的次数占尝试投篮次数的百分率)与尝试投篮次数x的情况,其中所有投进的球记2分,描述乙、丁两位同学情况的点恰好在同一个反比例函数的图像上,则投篮得分最多的是
A.甲 B.乙 C.丙 D.丁
9.在边长为1的正五边形内,所有到点的距离大于且到点的距离小于1的点组成图形的面积是
A. B.
C. D.
10.下列不可能是函数图象的是
A B C D
二、填空题(共6小题,每小题3分,共18分)
下列各题不需要写出解答过程,请将结果直接填写在答题卡指定的位置.
11.2024年全国新注册登记的新能源汽车预计约有1335万辆,将数据1335万用科学记数法表示为 .
12.写出一个图象经过第一、二、四象限的一次函数解析式是 .
13.化简的结果是 .
14.2024年4月25日20时59分,运载火箭托举着神舟十八号载人飞船,在酒泉卫星发射中心点火升空,送航天员奔赴“天宫”.如图,神舟十八号载人飞船从地面O处成功发射,当飞船到达点A时,地面D处的雷达站测得AD=4000米,仰角为37°,0.3秒后,飞船直线上升到达点B处,此时地面C处的雷达站测得B处的仰角为45°,点O,C,D在同一直线上,已知C,D两处相距460米,则飞船从A到B处的平均速度为 米/秒.(结果精确到1米;参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
15.已知抛物线与轴的两交点的横坐标为m,n,满足. 下列结论:
①;
②若,当时,随的增大而减小;
③若有一个根是大于的负数,则;
④.
其中正确的结论是________.(填写序号)
如图,在中,分别是边上的点,且.
则的最大值是 .
三、解答题(共8小题,共72分)
下列各题需要在答题卡指定的位置写出文字说明、证明过程、演算步骤或画出图形.
17.(本小题满分8分)
求满足不等式组的整数解.
18.(本小题满分8分)
如图,在平行四边形中,点E,F,G,H分别在边AB,BC,CD,DA上,且.
(1)求证:≌;
(2)请添加一个条件,使四边形为矩形(不需说明理由).
19.(本小题满分8分)
为了解武汉市初中生每周锻炼身体的时长t(单位:小时)的情况,在武汉市随机抽取部分初中生进行调查,按五个组别:A组(3t<4),B组(4t<5),C组(5t<6),D组(6t<7),E组(7t<8)进行整理,绘制如下两幅不完整的统计图.
所抽取学生周锻炼时长的频数直方图 所抽取学生周锻炼时长的扇形统计图
(1)这次抽样调查的样本容量为______;
(2)抽取的样本中,每周锻炼身体时长的中位数落在______组,A组所在扇形的圆心角大小是______;
(3)若武汉市共有250000名初中生,请估计每周锻炼时间不低于6小时的学生人数.
20.(本小题满分8分)
如图,AC是⊙O的弦,OD AC,连接OA,OC,点B在⊙O外,AB=AC,连接BC交OD于E,交OA于F,.
(1)求证:AB是⊙O的切线;
(2)若,,求⊙O的半径.
21.(本小题满分8分)
如图是由小正方形组成的网格,每个小正方形的顶点叫做格点,A,B,C都是格点.仅用无刻度的直尺在给定网格中完成画图.
(1)先在上画点,使平分,再画的中点;
(2)先画点,使四边形为平行四边形,再将绕点旋转得,使得的对应点落在直线上.
22.(本小题满分10分)
乒乓球是我国国球.球台长为2.8m,中间处球网的高度为1.5dm.现有一台乒乓球发球器,球从发球器出口到第一次接触台面的运动轨迹近似为一条直线.从第一次接触台面到第二次接触台面的运动轨迹近似为一条抛物线.乒乓球第一次接触台面在球网左侧,越过球网(擦网不影响球运动轨迹)后,第二次接触台面在球网右侧为成功发球.乒乓球大小忽略不计.如图,当发球器放在球台左端时,通过测量得到球距离台面高度y(单位:dm)与球距离发球器出口的水平距离x(单位:dm)的相关数据,如下表所示:
x(dm) 0 2 4 6 8 10 12 14 …
y(dm) 3.36 2.52 1.68 0.84 0 1.40 2.40 3 …
(1)直接写出球从发球器出口到第一次接触台面时y关于x的函数解析式;(写出自变量的取值范围)
(2)求乒乓球第二次接触台面时与发球器出口的水平距离;
(3)发球器有一个滑轨,可以让发球口向右平移,若要成功发球,发球口最多向右平移多少dm?
23.(本小题满分10分)
问题提出:如图1,是正方形边上一点,延长至使,四边形是正方形,,连,探究与的数量关系.
问题探究:(1)先将问题特殊化,如图2,当与重合时,直接写出与的数量关系;
(2)再探究一般情形,如图1,求与的数量关系.
问题拓展:(3)如图3,是矩形边上一点,,在的延长线上且,,矩形满足,若,求与的数量关系.
图1 图2 图3
24.(本小题满分12分)
抛物线交轴于A,B两点(A在B的左边),交y轴于点C.
(1)如图1,当时,
①直接写出A,B,C三点的坐标;
②抛物线的顶点为D,求证:∠DAB=∠ACB;
(2)如图2,将抛物线平移得到抛物线,其顶点为原点.过点P(0,1)的直线与抛物线交于M,N两点.直线QM,QN与抛物线只有一个交点,连接PQ,若PQ MN恒成立,求a.
图1 图2
同课章节目录
