【北师大版八上同步练习】 7.5 三角形的内角和定理(含答案)
文档属性
| 名称 | 【北师大版八上同步练习】 7.5 三角形的内角和定理(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 18.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-09 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【北师大版八上同步练习】 7.4三角形内角和定理
一、单选题
1.如图,,,则的度数是( )
A. B. C. D.
2.如图,中,弦相交于点,则( )
A. B. C. D.
3.线l1∥l2,一块含30°角的直角三角板如图所示放置,∠1=25°,则∠2等于( )
A.30° B.35° C.40° D.45°
4.将一副直角三角板如图放置,已知,,,则( )
A.45° B.60° C.75° D.105°
5.如图,在中,已知O为AC上一点,以为半径的圆经过点A,且与,分别交于点E,D.设,,则( )
A.若,则的度数为
B.若,则的度数为
C.若,则的度数为
D.若,则的度数为
二、填空题
6.如图,在中,,点D在上,于点交与点F.若,则 .
7.如图,在中,和的平分线相交于点P,若,则的度数为 .
8.如图,,点、分别是边、上的定点,点、分别是边、上的动点,记,,当最小时,则的值为 .
三、计算题
9.如图所示,已知∠A=48°,∠D=25°,FD⊥BC于E,求∠B的度数.
四、解答题
10.如图,在中,,,求的度数.
11.如图,已知,,将沿射线的方向平移至,使为的中点,连结,记与的交点为.
(1)求证:≌;
(2)若平分,求的度数.
12.如图1,AB,BC被直线AC所截,点是线段AC上的点,过点作,连接.
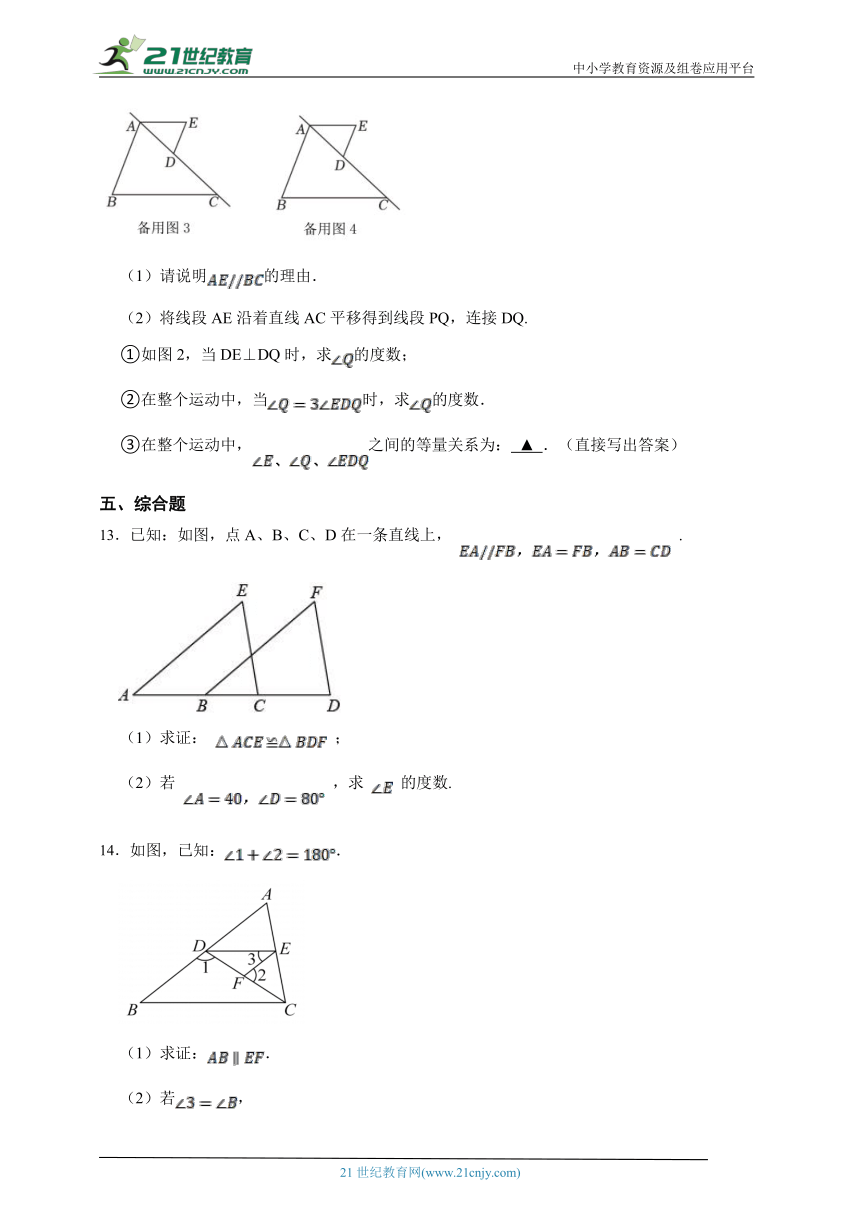
(1)请说明的理由.
(2)将线段AE沿着直线AC平移得到线段PQ,连接DQ.
①如图2,当DE⊥DQ时,求的度数;
②在整个运动中,当时,求的度数.
③在整个运动中,之间的等量关系为: ▲ .(直接写出答案)
五、综合题
13.已知:如图,点A、B、C、D在一条直线上, .
(1)求证: ;
(2)若 ,求 的度数.
14.如图,已知:.
(1)求证:.
(2)若,
①求证:.
②若,,则的度数为 ▲ .
15.在中,,点是直线上一点不与、重合,以为一边在的右侧作,使,,连接E.
(1)如图1,当点在线段上,如果.
①则与全等吗?请说明理由;
②求的度数;
(2)如图2,如果,当点在线段上移动,则的度数是 ;
(3)如图2,当点在线段上,如果,点为中边上的一个动点与、均不重合,当点运动到什么位置时,的周长最小?
六、实践探究题
16.在沪科版数学八年级上册第80页探索了“三角形的内角和等于180°”,晓波在研究完上面的问题后,对这个图形进行了深入的研究,他的研究过程如下:
(1)【图形再现】
如图1,对任意三角形,延长到,过点作的平行线,就可以证明:,即三角形的内角和等于180°,请完成上述证明过程;
(2)【图形探究】
如图2,在中,的平分线与的平分线交于点,过点作,点在射线上,且,的延长线与的延长线交于点.
①求的度数;
②探究与的数量关系,并说明理由.
17.将一个直角三角形纸板ABC放置在锐角△PMN上,使该直角三角形纸板的两条直角边AB,AC分别经过点M,N.
【发现】
(1)如图1,若点A在△PMN内,当∠P=40°时,则∠PMA+∠PNA= ;
(2)如图2,若点A在△PMN内,当∠P=60°时,∠PMA+∠PNA= ;
(3)【探究】
若点A在△PMN内,请你判断∠PMA,∠PNA和∠P之间满足怎样的数量关系,并写出理由;
(4)【应用】
如图3,点A在△PMN内,过点P作直线EF∥AB,若∠PNA=18°,求∠NPE的度数;
(5)【拓展】
如图4,当点A在△PMN外,请直接写出∠PMA,∠PNA和∠P之间满足的数量关系 .
18.已知直线 , 点 为平行线 之间的一点, 如图 1 所示,若 平分 平分 .
(1) 则 , .
(2)【探究】如图 2 所示, 当点 在直线 的上方时, 若 , 和 的平分线交于点 与 的角平分线交于点 , 与 的角平分线交于点 以此类推, 求 的度数, 并猜想 的度数.
(3)【变式】如图 3 所示, 的角平分线的反向延长线和 的补角的角平分线交于点 , 试直接写出 与 的数量关系.
答案解析部分
1.【答案】C
【知识点】三角形的外角性质
2.【答案】D
【知识点】三角形的外角性质;圆周角定理
3.【答案】B
【知识点】三角形的外角性质;同位角
4.【答案】C
【知识点】平行线的性质;三角形内角和定理;三角形的外角性质
5.【答案】B
【知识点】三角形内角和定理;三角形的外角性质;圆周角定理
6.【答案】42°
【知识点】三角形内角和定理;等腰三角形的性质
7.【答案】116°
【知识点】三角形内角和定理;角平分线的定义
8.【答案】40°
【知识点】三角形的外角性质;轴对称的性质;轴对称的应用-最短距离问题
9.【答案】解:∵∠A=48°,∠D=25°,
∴∠BFE=∠A+∠D=73°(三角形外角定理);
又∵FD⊥BC于E,
∴∠BEF=90°;
∴Rt△BFE中,∠B=180°﹣∠BEF﹣∠BFE=17°,即∠B=17°.
【知识点】三角形内角和定理
10.【答案】解:,
,
,,
.
【知识点】垂线;三角形内角和定理
11.【答案】(1)证明:由平移可知,AB=A'B',AB∥A'B',
∴四边形ABB'A'是平行四边形,
∴AA'=BB',AA'∥BB',
∴∠A'AO=∠C=50°,
∵点B'是BC的中点,
∴BB'=CB',
∴B'C=AA',
在△AOA'与△COB'中,
∵∠A'AO=∠C,∠AOA'=∠COB',B'C=AA'
∴△AOA'≌△COB'(AAS);
(2)解:平分,∠A'AO=∠C=50°,
,
.
【知识点】三角形内角和定理;平行四边形的判定与性质;平移的性质;三角形全等的判定(AAS);角平分线的定义
12.【答案】(1)解:,
(2)解:①如图2,过D作交AB于,
线段AE沿着直线AC平移得到线段PQ,
,
,
,
②当P点在AD之间,如图3,过作交AB于,
由
;
当点在DA的延长线上,如图4,过作交AB于,
,
,
,
,
,
,
,
由
,
,
综上所述,或,
③.
【知识点】平行线的判定;平行线的性质;三角形内角和定理
13.【答案】(1)证明:∵EA∥FB,
∴∠A=∠FBD,
∵AB=CD,
∴AB+BC=CD+BC,
即AC=BD,
在△EAC与△FBD中,
∴△EAC≌△FBD(SAS)
(2)解:∵△EAC≌△FBD,
∴∠ECA=∠D=80°,
∵∠A=40°,
∴∠E=180°-40°-80°=60°,
答:∠E的度数为60°.
【知识点】三角形内角和定理;三角形全等的判定(SAS)
14.【答案】(1)解:,
(2)解:①由(1)可知,
;
②
【知识点】平行线的判定与性质;三角形内角和定理
15.【答案】(1)解:①与全等
证明:,
,即.
在与中,
,
②,
,
,
,
,
,
,
(2)
(3)解:当点运动到中点时,的周长最小.
,
,
为等边三角形
,
的周长
;
当最小时,即当点运动到中点时,的周长最小.
【知识点】垂线段最短;三角形内角和定理;三角形全等及其性质;三角形全等的判定;等腰三角形的性质
16.【答案】(1)证明:由题意知,
,.
,
,即三角形的内角和等于180°.
(2)解:如图.
①,.
是的平分线,
,.
又,,
,,
②
理由:是的平分线,.
在中,,即.
,.
又,,
,
,
.
【知识点】平行线的性质;三角形内角和定理;三角形的外角性质;角平分线的性质
17.【答案】(1)50°
(2)30
(3)解:∠PMA+∠PNA+∠P=90°理由如下:
∵△ABC是直角三角形,
∴∠BAC=90°,
∴∠AMN+∠ANM=90°,
∴∠PMN+∠PNM=180°﹣∠P,
∴∠PMA+∠AMN+∠ANM+∠PNA=180°﹣∠P,
∴∠PMA+∠PNA+(∠AMN+∠ANM)=180°﹣∠P﹣90°=90°﹣∠P,
即:∠PMA+PNA+∠P=90°
(4)解:∠NPE=108°理由如下:
由上可知,∠PMA+PNA+∠MPN=90°,
∵∠PNA=18°,
∴∠PMA+∠MPN=90°﹣∠PNA=72°,
∵EFAB,
∴∠PMA=∠FPM,
∴∠FPM+∠MPN=72°,
即:∠FPN=72°,
∴∠NPE=180°﹣∠FPN=108°,
(5)∠PMA+∠PNA+∠P=270°
【知识点】平行线的性质;三角形内角和定理;直角三角形的性质
18.【答案】(1)110°;55°
(2)解:∵∠ABP与∠CDP的平分线交于点E1
∴∠ABE1=∠ABP=α,∠CDE1=∠CDP=β
∵AB∥CD
∴∠CDF=∠AFE1=β
∴∠E1=∠AFE1-∠ABE1=β-α=(β-α)
∵∠ABE1与∠CDE1的角平分线交于点E2
∴∠ABE2=∠CDE1=α,∠CDE2=∠CDE1=β
∴∠E2=∠AGE2-∠ABE2=(β-α)
同理,可得∠E3=(β-α);
以此类推,可得∠En=(β-α).
(3)解:∠E=∠DEB=90°-∠P;
过点E作EG∥AB,可得AB∥EG∥CD,如下图:
∵AB∥EG∥CD
∴∠MBE=∠BEG,∠FDE=∠GED
∴∠DEB=∠BEG+∠DEG=∠MBE+∠FDE=∠ABQ+∠FDE
∵∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E
∴∠FDE=∠PDF=(180°-∠CDP),∠ABQ=∠ABP
∴∠DEB=∠ABP+(180°-∠CDP)=90°-(∠CDP-∠ABP)
∵AB∥CD
∴∠CDP=∠AHP
∴∠DEP=90°-(∠CDP-∠ABP)=90°-(∠AHP-∠ABP)=90°-∠P
【知识点】角的运算;平行公理及推论;平行线的性质;三角形内角和定理;三角形的外角性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【北师大版八上同步练习】 7.4三角形内角和定理
一、单选题
1.如图,,,则的度数是( )
A. B. C. D.
2.如图,中,弦相交于点,则( )
A. B. C. D.
3.线l1∥l2,一块含30°角的直角三角板如图所示放置,∠1=25°,则∠2等于( )
A.30° B.35° C.40° D.45°
4.将一副直角三角板如图放置,已知,,,则( )
A.45° B.60° C.75° D.105°
5.如图,在中,已知O为AC上一点,以为半径的圆经过点A,且与,分别交于点E,D.设,,则( )
A.若,则的度数为
B.若,则的度数为
C.若,则的度数为
D.若,则的度数为
二、填空题
6.如图,在中,,点D在上,于点交与点F.若,则 .
7.如图,在中,和的平分线相交于点P,若,则的度数为 .
8.如图,,点、分别是边、上的定点,点、分别是边、上的动点,记,,当最小时,则的值为 .
三、计算题
9.如图所示,已知∠A=48°,∠D=25°,FD⊥BC于E,求∠B的度数.
四、解答题
10.如图,在中,,,求的度数.
11.如图,已知,,将沿射线的方向平移至,使为的中点,连结,记与的交点为.
(1)求证:≌;
(2)若平分,求的度数.
12.如图1,AB,BC被直线AC所截,点是线段AC上的点,过点作,连接.
(1)请说明的理由.
(2)将线段AE沿着直线AC平移得到线段PQ,连接DQ.
①如图2,当DE⊥DQ时,求的度数;
②在整个运动中,当时,求的度数.
③在整个运动中,之间的等量关系为: ▲ .(直接写出答案)
五、综合题
13.已知:如图,点A、B、C、D在一条直线上, .
(1)求证: ;
(2)若 ,求 的度数.
14.如图,已知:.
(1)求证:.
(2)若,
①求证:.
②若,,则的度数为 ▲ .
15.在中,,点是直线上一点不与、重合,以为一边在的右侧作,使,,连接E.
(1)如图1,当点在线段上,如果.
①则与全等吗?请说明理由;
②求的度数;
(2)如图2,如果,当点在线段上移动,则的度数是 ;
(3)如图2,当点在线段上,如果,点为中边上的一个动点与、均不重合,当点运动到什么位置时,的周长最小?
六、实践探究题
16.在沪科版数学八年级上册第80页探索了“三角形的内角和等于180°”,晓波在研究完上面的问题后,对这个图形进行了深入的研究,他的研究过程如下:
(1)【图形再现】
如图1,对任意三角形,延长到,过点作的平行线,就可以证明:,即三角形的内角和等于180°,请完成上述证明过程;
(2)【图形探究】
如图2,在中,的平分线与的平分线交于点,过点作,点在射线上,且,的延长线与的延长线交于点.
①求的度数;
②探究与的数量关系,并说明理由.
17.将一个直角三角形纸板ABC放置在锐角△PMN上,使该直角三角形纸板的两条直角边AB,AC分别经过点M,N.
【发现】
(1)如图1,若点A在△PMN内,当∠P=40°时,则∠PMA+∠PNA= ;
(2)如图2,若点A在△PMN内,当∠P=60°时,∠PMA+∠PNA= ;
(3)【探究】
若点A在△PMN内,请你判断∠PMA,∠PNA和∠P之间满足怎样的数量关系,并写出理由;
(4)【应用】
如图3,点A在△PMN内,过点P作直线EF∥AB,若∠PNA=18°,求∠NPE的度数;
(5)【拓展】
如图4,当点A在△PMN外,请直接写出∠PMA,∠PNA和∠P之间满足的数量关系 .
18.已知直线 , 点 为平行线 之间的一点, 如图 1 所示,若 平分 平分 .
(1) 则 , .
(2)【探究】如图 2 所示, 当点 在直线 的上方时, 若 , 和 的平分线交于点 与 的角平分线交于点 , 与 的角平分线交于点 以此类推, 求 的度数, 并猜想 的度数.
(3)【变式】如图 3 所示, 的角平分线的反向延长线和 的补角的角平分线交于点 , 试直接写出 与 的数量关系.
答案解析部分
1.【答案】C
【知识点】三角形的外角性质
2.【答案】D
【知识点】三角形的外角性质;圆周角定理
3.【答案】B
【知识点】三角形的外角性质;同位角
4.【答案】C
【知识点】平行线的性质;三角形内角和定理;三角形的外角性质
5.【答案】B
【知识点】三角形内角和定理;三角形的外角性质;圆周角定理
6.【答案】42°
【知识点】三角形内角和定理;等腰三角形的性质
7.【答案】116°
【知识点】三角形内角和定理;角平分线的定义
8.【答案】40°
【知识点】三角形的外角性质;轴对称的性质;轴对称的应用-最短距离问题
9.【答案】解:∵∠A=48°,∠D=25°,
∴∠BFE=∠A+∠D=73°(三角形外角定理);
又∵FD⊥BC于E,
∴∠BEF=90°;
∴Rt△BFE中,∠B=180°﹣∠BEF﹣∠BFE=17°,即∠B=17°.
【知识点】三角形内角和定理
10.【答案】解:,
,
,,
.
【知识点】垂线;三角形内角和定理
11.【答案】(1)证明:由平移可知,AB=A'B',AB∥A'B',
∴四边形ABB'A'是平行四边形,
∴AA'=BB',AA'∥BB',
∴∠A'AO=∠C=50°,
∵点B'是BC的中点,
∴BB'=CB',
∴B'C=AA',
在△AOA'与△COB'中,
∵∠A'AO=∠C,∠AOA'=∠COB',B'C=AA'
∴△AOA'≌△COB'(AAS);
(2)解:平分,∠A'AO=∠C=50°,
,
.
【知识点】三角形内角和定理;平行四边形的判定与性质;平移的性质;三角形全等的判定(AAS);角平分线的定义
12.【答案】(1)解:,
(2)解:①如图2,过D作交AB于,
线段AE沿着直线AC平移得到线段PQ,
,
,
,
②当P点在AD之间,如图3,过作交AB于,
由
;
当点在DA的延长线上,如图4,过作交AB于,
,
,
,
,
,
,
,
由
,
,
综上所述,或,
③.
【知识点】平行线的判定;平行线的性质;三角形内角和定理
13.【答案】(1)证明:∵EA∥FB,
∴∠A=∠FBD,
∵AB=CD,
∴AB+BC=CD+BC,
即AC=BD,
在△EAC与△FBD中,
∴△EAC≌△FBD(SAS)
(2)解:∵△EAC≌△FBD,
∴∠ECA=∠D=80°,
∵∠A=40°,
∴∠E=180°-40°-80°=60°,
答:∠E的度数为60°.
【知识点】三角形内角和定理;三角形全等的判定(SAS)
14.【答案】(1)解:,
(2)解:①由(1)可知,
;
②
【知识点】平行线的判定与性质;三角形内角和定理
15.【答案】(1)解:①与全等
证明:,
,即.
在与中,
,
②,
,
,
,
,
,
,
(2)
(3)解:当点运动到中点时,的周长最小.
,
,
为等边三角形
,
的周长
;
当最小时,即当点运动到中点时,的周长最小.
【知识点】垂线段最短;三角形内角和定理;三角形全等及其性质;三角形全等的判定;等腰三角形的性质
16.【答案】(1)证明:由题意知,
,.
,
,即三角形的内角和等于180°.
(2)解:如图.
①,.
是的平分线,
,.
又,,
,,
②
理由:是的平分线,.
在中,,即.
,.
又,,
,
,
.
【知识点】平行线的性质;三角形内角和定理;三角形的外角性质;角平分线的性质
17.【答案】(1)50°
(2)30
(3)解:∠PMA+∠PNA+∠P=90°理由如下:
∵△ABC是直角三角形,
∴∠BAC=90°,
∴∠AMN+∠ANM=90°,
∴∠PMN+∠PNM=180°﹣∠P,
∴∠PMA+∠AMN+∠ANM+∠PNA=180°﹣∠P,
∴∠PMA+∠PNA+(∠AMN+∠ANM)=180°﹣∠P﹣90°=90°﹣∠P,
即:∠PMA+PNA+∠P=90°
(4)解:∠NPE=108°理由如下:
由上可知,∠PMA+PNA+∠MPN=90°,
∵∠PNA=18°,
∴∠PMA+∠MPN=90°﹣∠PNA=72°,
∵EFAB,
∴∠PMA=∠FPM,
∴∠FPM+∠MPN=72°,
即:∠FPN=72°,
∴∠NPE=180°﹣∠FPN=108°,
(5)∠PMA+∠PNA+∠P=270°
【知识点】平行线的性质;三角形内角和定理;直角三角形的性质
18.【答案】(1)110°;55°
(2)解:∵∠ABP与∠CDP的平分线交于点E1
∴∠ABE1=∠ABP=α,∠CDE1=∠CDP=β
∵AB∥CD
∴∠CDF=∠AFE1=β
∴∠E1=∠AFE1-∠ABE1=β-α=(β-α)
∵∠ABE1与∠CDE1的角平分线交于点E2
∴∠ABE2=∠CDE1=α,∠CDE2=∠CDE1=β
∴∠E2=∠AGE2-∠ABE2=(β-α)
同理,可得∠E3=(β-α);
以此类推,可得∠En=(β-α).
(3)解:∠E=∠DEB=90°-∠P;
过点E作EG∥AB,可得AB∥EG∥CD,如下图:
∵AB∥EG∥CD
∴∠MBE=∠BEG,∠FDE=∠GED
∴∠DEB=∠BEG+∠DEG=∠MBE+∠FDE=∠ABQ+∠FDE
∵∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E
∴∠FDE=∠PDF=(180°-∠CDP),∠ABQ=∠ABP
∴∠DEB=∠ABP+(180°-∠CDP)=90°-(∠CDP-∠ABP)
∵AB∥CD
∴∠CDP=∠AHP
∴∠DEP=90°-(∠CDP-∠ABP)=90°-(∠AHP-∠ABP)=90°-∠P
【知识点】角的运算;平行公理及推论;平行线的性质;三角形内角和定理;三角形的外角性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
