【北师大版八上同步练习】 第七章 平行线的证明(培优)检测题(含答案)
文档属性
| 名称 | 【北师大版八上同步练习】 第七章 平行线的证明(培优)检测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 17.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-09 17:15:02 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【北师大版八上同步练习】
第七章平行线的证明(培优)检测题
一、单选题
1.如图,点E在BC的延长线上,下列条件不能判定的是( )
A. B.
C. D.
2.把一块直尺与一块三角板如图放置,若,则的度数为( )
A. B. C. D.
3.如图所示,光在不同介质中的传播速度不同,因此当光线从空气射向水中时,会发生折射,在空气中平行的两条入射光线,在水中的两条折射光线也是平行的.若水面和杯底互相平行,且,则( ).
A.58° B.68° C.32° D.122°
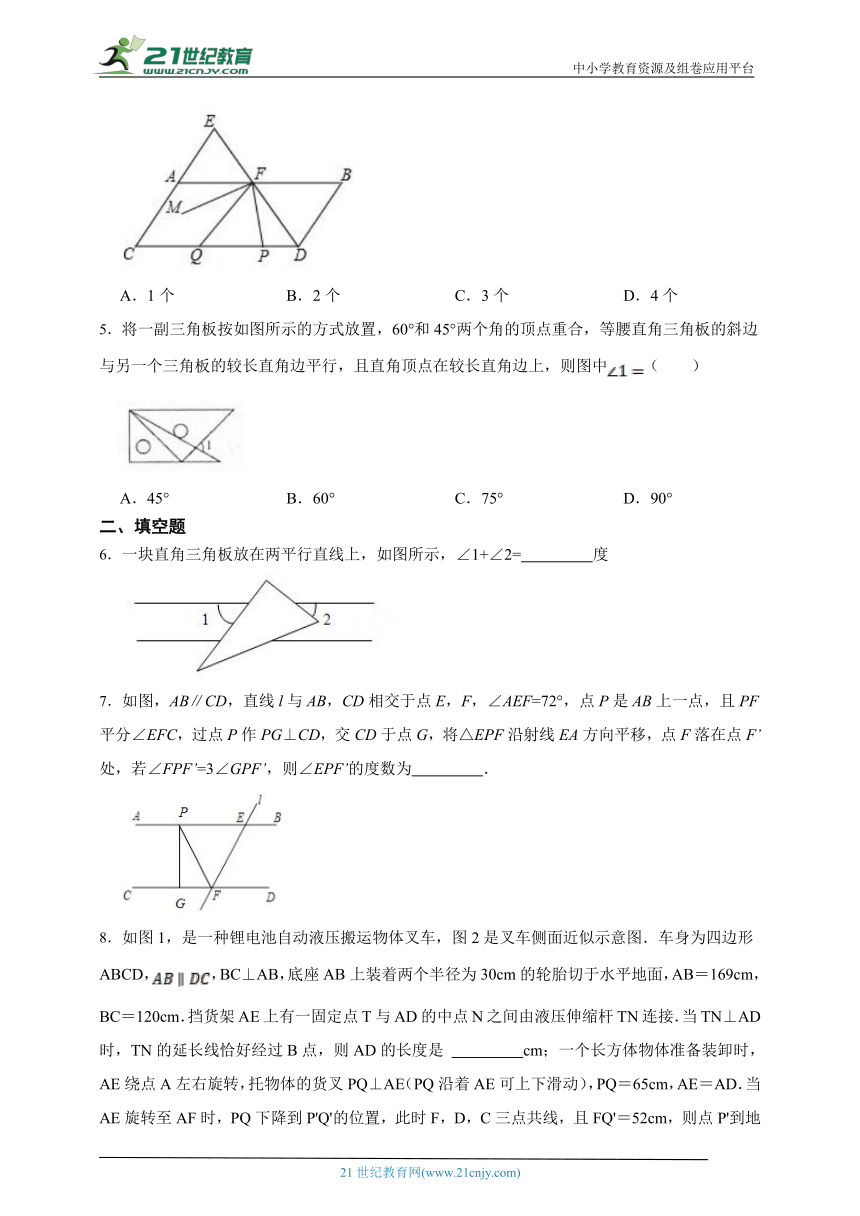
4.如图5,点在延长线上,交于,且,,比的余角小,为线段上一动点,为上一点,且满足,为的平分线.则下列结论:①;②平分;③;④的角度为定值.
其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
5.将一副三角板按如图所示的方式放置,60°和45°两个角的顶点重合,等腰直角三角板的斜边与另一个三角板的较长直角边平行,且直角顶点在较长直角边上,则图中( )
A.45° B.60° C.75° D.90°
二、填空题
6.一块直角三角板放在两平行直线上,如图所示,∠1+∠2= 度
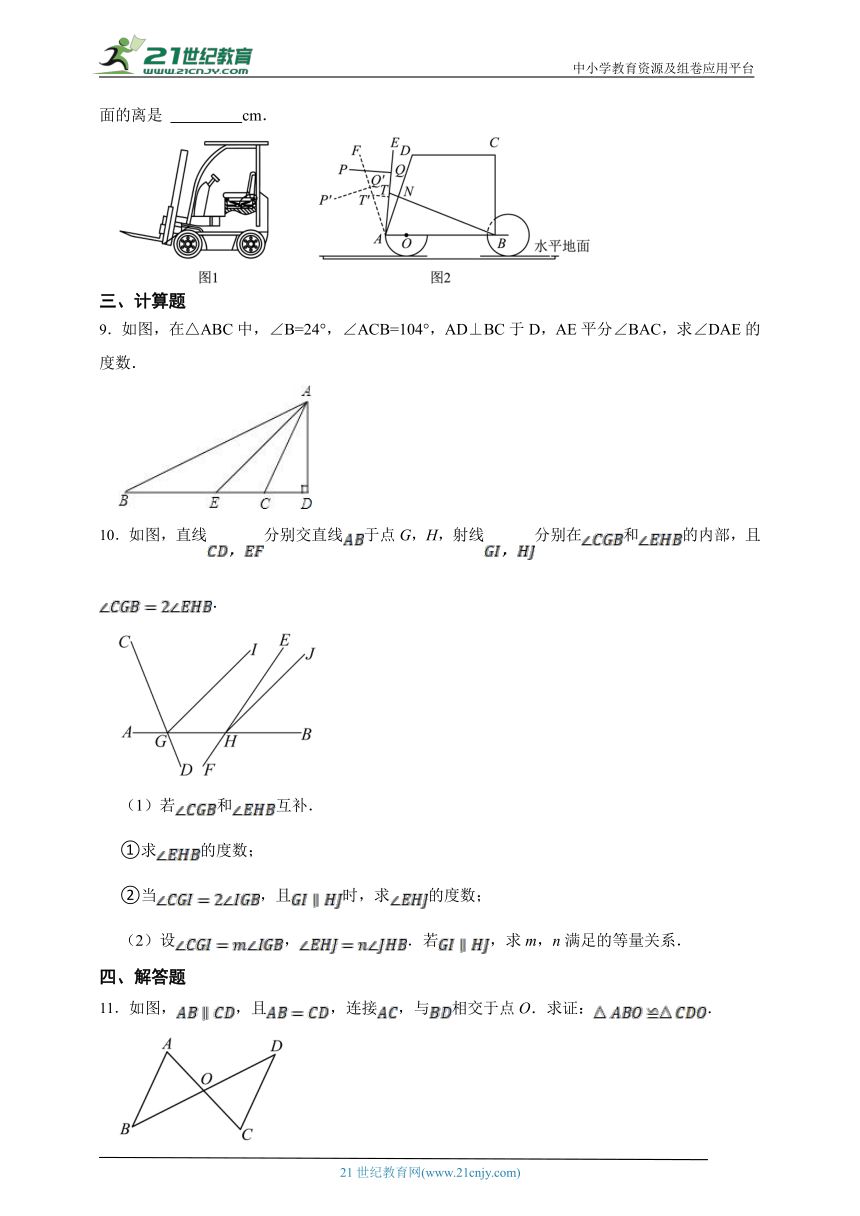
7.如图,AB∥CD,直线l与AB,CD相交于点E,F,∠AEF=72°,点P是AB上一点,且PF平分∠EFC,过点P作PG⊥CD,交CD于点G,将△EPF沿射线EA方向平移,点F落在点F’处,若∠FPF’=3∠GPF’,则∠EPF’的度数为 .
8.如图1,是一种锂电池自动液压搬运物体叉车,图2是叉车侧面近似示意图.车身为四边形ABCD,,BC⊥AB,底座AB上装着两个半径为30cm的轮胎切于水平地面,AB=169cm,BC=120cm.挡货架AE上有一固定点T与AD的中点N之间由液压伸缩杆TN连接.当TN⊥AD时,TN的延长线恰好经过B点,则AD的长度是 cm;一个长方体物体准备装卸时,AE绕点A左右旋转,托物体的货叉PQ⊥AE(PQ沿着AE可上下滑动),PQ=65cm,AE=AD.当AE旋转至AF时,PQ下降到P'Q'的位置,此时F,D,C三点共线,且FQ'=52cm,则点P'到地面的离是 cm.
三、计算题
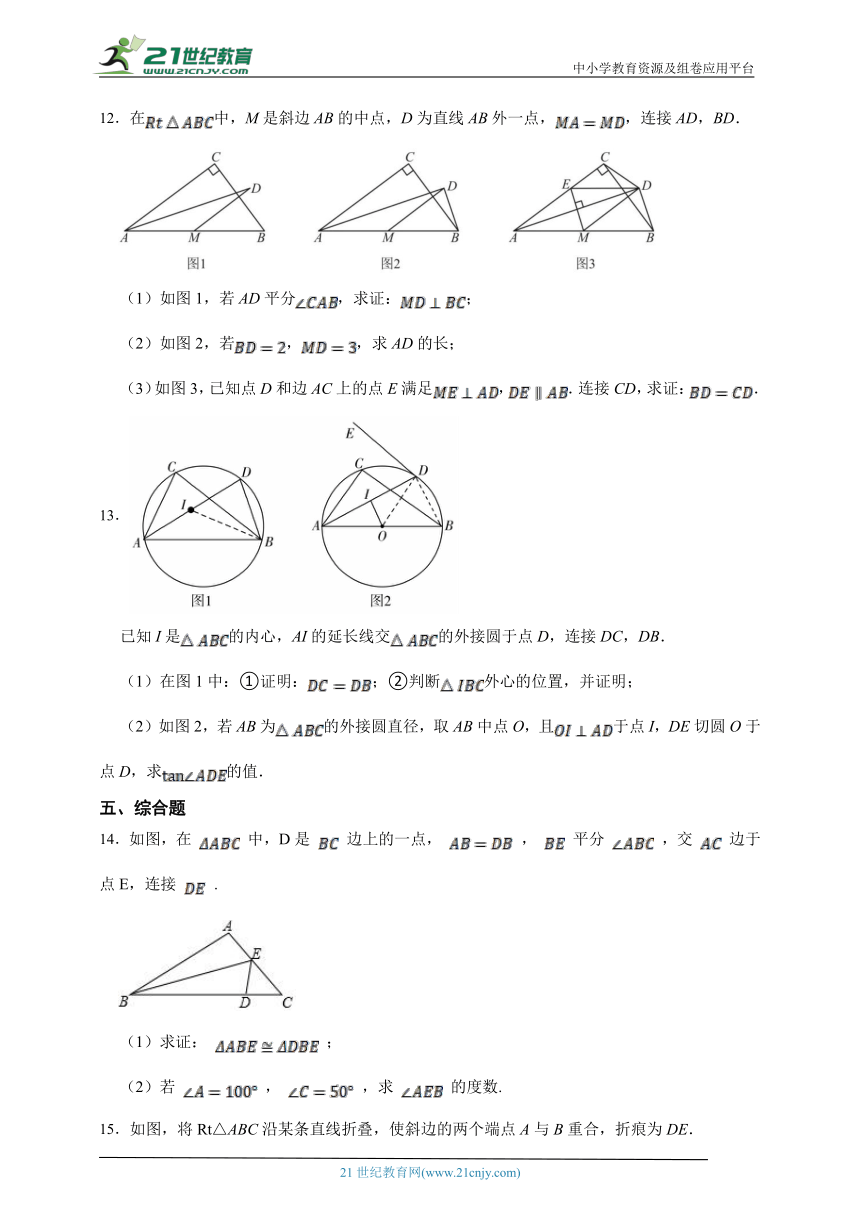
9.如图,在△ABC中,∠B=24°,∠ACB=104°,AD⊥BC于D,AE平分∠BAC,求∠DAE的度数.
10.如图,直线分别交直线于点G,H,射线分别在和的内部,且.
(1)若和互补.
①求的度数;
②当,且时,求的度数;
(2)设,.若,求m,n满足的等量关系.
四、解答题
11.如图,,且,连接,与相交于点O.求证:.
12.在中,M是斜边AB的中点,D为直线AB外一点,,连接AD,BD.
(1)如图1,若AD平分,求证:;
(2)如图2,若,,求AD的长;
(3)如图3,已知点D和边AC上的点E满足,.连接CD,求证:.
13.
已知I是的内心,AI的延长线交的外接圆于点D,连接DC,DB.
(1)在图1中:①证明:;②判断外心的位置,并证明;
(2)如图2,若AB为的外接圆直径,取AB中点O,且于点I,DE切圆O于点D,求的值.
五、综合题
14.如图,在 中,D是 边上的一点, , 平分 ,交 边于点E,连接 .
(1)求证: ;
(2)若 , ,求 的度数.
15.如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)如果AC=6cm,BC=8cm,试求△ACD的周长;
(2)如果∠CAD:∠BAD=1:2,求∠B的度数.
16.如图,二次函数的图象与x轴交于点和点B,与y轴交于点C,且顶点D的坐标为,对称轴与直线交于点E,与x轴交于点F,连接,.
(1)求二次函数的解析式;
(2)点P在上方二次函数图象上,且的面积等于6,求点P的坐标;
(3)在二次函数图象上是否存在一点M,使得?若存在,求出直线与x轴的交点Q的坐标;若不存在,请说明理由.
六、实践探究题
17.在物理学中,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
如图1,一束光线射到平面镜上,被反射后的光线为,则入射光线、反射光线与平面镜所夹的锐角.
(1)【简单应用】
如图2,有一口井,已知入射光线与水平线的夹角为,现放置平面镜,可使反射光线正好垂直照射到井底(即射线),与水平线的夹角的度数为 .
(2)【类比拓展】
如图3,有两块平面镜,且,入射光线经过两次反射,得到反射光线.由以上光的反射定律,可知入射角与反射角相等,进而可以推得他们的余角也相等,即:.在这样的条件下,求证:.
(3)【尝试探究】
两块平面镜,且,入射光线经过两次反射,得到反射光线.如图4,光线与相交于点,则的度数是多少?(用含的式子表示)(三角形内角和)
18.
(1)问题发现:
如图①,直线AB∥CD,连接BE,CE,可以发现∠B+∠C=∠BEC,请把下面的证明过程补充完整:
证明:过点E作EF∥AB,
∵AB∥DC(已知)
∴EF∥DC( ).
∴∠C=∠CEF.( ).
∵EF∥AB,
∴∠B=∠BEF (同理).
∴∠B+∠C= (等量代换),即∠B+∠C=∠BEC.
(2)拓展探究:
如果点E运动到图②所示的位置,其他条件不变,说明:∠B+∠C+∠BEC=360°.
(3)解决问题:如图③,AB∥DC,E、F、G是AB与CD之间的点,直接写出∠1,∠2,∠3,∠4,∠5之间的数量关系.
19. 综合实践.
我们发现平行线具有“等角转化”的功能,通过添加平行线可将不同位置的角“凑”在一起,得出角之间的关系.根据平行线的“等角转化”功能,解答下列问题:
(1)阅读理解:如图1,相交于点,请说明.阅读并补充下面推理过程.
解:如图1,过点作.
_▲_.
,
_▲_.
_▲_.
.
即.
(2)方法掌握:如图2,已知交于点.请写出之间的数量关系,并证明你的结论;
(3)拓展运用:如图3,已知,点在直线上,平分平分.若,求度数(用含的式子表示).
答案解析部分
1.【答案】C
【知识点】平行线的判定
2.【答案】D
【知识点】角的运算;平行线的性质
3.【答案】A
【知识点】平行线的性质
4.【答案】D
【知识点】余角、补角及其性质;平行线的判定与性质
5.【答案】C
【知识点】平行线的性质;三角形的外角性质
6.【答案】90
【知识点】平行线的性质;直角三角形的性质
7.【答案】108°
【知识点】平行线的性质;平移的性质;角平分线的定义
8.【答案】130;77
【知识点】平行线的判定与性质;三角形全等及其性质;勾股定理;锐角三角函数的定义
9.【答案】解:在△ABC中,
∵∠BAC+∠B+∠ACB=180°,∠B=24°,∠ACB=104°,
∴∠BAC=180°﹣∠B﹣∠ACB=180°﹣24°﹣104°=52°.
∵AE平分∠BAC,
∴∠EAC= ∠BAC= 52°=26°,
∵AD⊥BC,
∴∠ADC=90°,
∵∠ACB=104°,
∴∠ACD=180°﹣∠ACB=180°﹣104°=76°,
∴∠CAD=14°,
∴∠DAE=∠EAC+∠CAD=40°
【知识点】三角形内角和定理;三角形的外角性质
10.【答案】(1)解:①和互补,
.
,
,
;
②由①得,
,
,
又,
,
.
,
,
;
(2)解:,
.
设,
,,
,
,
又,
,
,
,
即m,n满足的等量关系为.
【知识点】角的运算;平行线的性质;邻补角
11.【答案】证明:,
,,
在与中,
,
.
【知识点】平行线的性质;三角形全等的判定(ASA)
12.【答案】(1)证明:如图,MD与BC交于点E,
∵AD平分,∴,
∵,∴,
∴,∴,
又∵是直角三角形,,
∴,∴;
(2)解:∵M是斜边AB的中点,,
∴,∴,,
在中,,
∴,
∵,,∴,
由勾股定理得:;
(3)证明:如图,延长BD、AC,交于点F,
则,
∵,,∴.
又∵,∴四边形BDEM是平行四边形.∴.
∵M是AB的中点,∴.
∴.∴四边形AMDE是平行四边形.
∵,∴平行四边形AMDE是菱形.∴.
∵,∴,,
∴,∴,
即点D是斜边的中点.∴.
【知识点】平行线的性质;勾股定理;平行四边形的判定;菱形的判定;三角形全等的判定(ASA);角平分线的定义;直角三角形斜边上的中线
13.【答案】(1)解:①
∵I是的内心
∴AI平分,
∴
②D为外心,证明如下:
∵I是的内心
∴BI平分,,∵,
∴
∴,即
∴D为外心
(2)解:连接OD
∵AB为的外接圆直径,O为AB中点
∴O为的外接圆圆心
∵DE切圆O于点D
∴,即,
∵,∴,
∵AB为的外接圆直径
∴,∴,
∵,,∴
∵由(1)得,∴
∴
【知识点】圆周角定理;三角形的外接圆与外心;解直角三角形
14.【答案】(1)证明: 平分 ,
,
在 和 中, ,
;
(2)解: , ,
,
平分 ,
,
在 中, .
【知识点】三角形内角和定理;三角形全等的判定(SAS);角平分线的定义
15.【答案】(1)由折叠的性质可知,DE垂直平分线段AB,
根据垂直平分线的性质可得:DA=DB,
所以,DA+DC+AC=DB+DC+AC=BC+AC=14cm;
(2)设∠CAD=x,则∠BAD=2x,
∵DA=DB,
∴∠B=∠BAD=2x,
在Rt△ABC中,∠B+∠BAC=90°,
即:2x+2x+x=90°,x=18°,
∠B=2x=36°.
【知识点】角的运算;余角、补角及其性质;线段垂直平分线的性质;轴对称的性质;翻折变换(折叠问题)
16.【答案】(1)解:设二次函数的解析式为设二次函数的解析式为y=a(x﹣h)2+k
把顶点D(﹣2,8)代入,得
y= a(x +2)2+8.把点(﹣6,0)代入得:
0= a(﹣6+2)2+8.
∴ a =﹣
∴二次函数的解析式为y=﹣(x +2)2+8;
(2)解:∵y=﹣(x +2)2+8=﹣x2﹣2x+6
∴C(0,6),
设直线AC的解析式为y=kx+b,把A,C的坐标代入,得
解得:
直线AC的解析式为y=x+6,
∵二次函数的对称轴是直线,
∴E点的横坐标是-2
∴
∴
∴
∴DE=4,
∴
∴h=3,
∴P点的横坐标为-5,
∴
∴
(3)解:存在
∵A(﹣6,0) ,C(0,6)
∴ OA=OC=6
∴△ AOC为等腰直角三角形,
∴∠ ACO= 45°
令y=0
0=﹣x2﹣2x+6
解得:x1=2,x2=﹣6
∴点B(2,0)
①当CM在∠ ACO内部时,如图
∵∠ACM + ∠OCB=45°,∠ACM+∠MCO=∠ ACO= 45°
∴∠OCB=∠MCO
∴OQ=OB=2
∴点Q(﹣2,0)
②当CM在∠ ACO外部时,如图:
∵∠ACM + ∠OCB=45°,∠ ACO= 45°
∴∠BCQ=90°
设点Q(t,0)
则BQ=2- t
CQ2=OC2+OQ2= t 2+62
BC2=OB2+OC2=22+62
∵BQ2= CQ2+ BC2
∴(2﹣ t)2= t 2+62+22+62
t =﹣18
综上所述,直线CM与x轴的交点Q的坐标为(﹣2,0)或(﹣18,0).
【知识点】待定系数法求二次函数解析式;三角形的面积;勾股定理;等腰直角三角形;二次函数图象上点的坐标特征
17.【答案】(1)65°
(2)解:如图1,∵OM⊥ON,
∴∠CON=90°,
∴∠2+∠3=90°,
∵∠1=∠2,∠3=∠4,
∴∠1+∠2+∠3+∠4=180°,
∠DCB+∠ABC=180°,
AB∥CD;
(3)解:如图4,在△OBC中,
∵∠MON=α,
∴∠2+∠3=180°﹣α,
∵∠1=∠2,∠3=∠4,
∴
∴∠BEC=180°﹣∠ABC﹣∠BCD
=180°﹣(180°﹣2∠2)﹣(180°﹣2∠3)
=2(∠2+∠3)﹣180°
=2(180°﹣a)﹣180°
=180°﹣2α,
故答案为:180°﹣2α;
【知识点】垂线;平行线的性质
18.【答案】(1)平行于同一直线的两直线平行;两直线平行,内错角相等;∠BEF+∠CEF
(2)解:如图②,过点E作EF∥AB,
∵AB∥CD,EF∥AB,
∴EF∥CD,
∴∠C+∠CEF=180°,∠B+∠BEF=180°,
∴∠B+∠C+∠BEC=360°,
∴∠B+∠C=360°﹣(∠BEF+∠CEF),
即∠B+∠C+∠BEC=360°;
(3)解:∠1+∠3+∠5=∠2+∠4,理由如下:
如图,过点F作FM∥AB,则AB∥FM∥CD,
由(1)得,∠1+∠3+∠5=∠2+∠4.
【知识点】平行公理及推论;平行线的判定与性质
19.【答案】(1)解:如图1,过点P作,
∴
∵
∴
∴
∴
即
(2)解:,理由如下:
过点M作,如图2:
∴,
∵
∴
∴
∵
∴
∴
即
(3)解:,理由如下:
∵平分平分
∴
∵
∴
∵,
∴
∴
即
【知识点】平行公理及推论;平行线的性质;三角形内角和定理;角平分线的定义
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【北师大版八上同步练习】
第七章平行线的证明(培优)检测题
一、单选题
1.如图,点E在BC的延长线上,下列条件不能判定的是( )
A. B.
C. D.
2.把一块直尺与一块三角板如图放置,若,则的度数为( )
A. B. C. D.
3.如图所示,光在不同介质中的传播速度不同,因此当光线从空气射向水中时,会发生折射,在空气中平行的两条入射光线,在水中的两条折射光线也是平行的.若水面和杯底互相平行,且,则( ).
A.58° B.68° C.32° D.122°
4.如图5,点在延长线上,交于,且,,比的余角小,为线段上一动点,为上一点,且满足,为的平分线.则下列结论:①;②平分;③;④的角度为定值.
其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
5.将一副三角板按如图所示的方式放置,60°和45°两个角的顶点重合,等腰直角三角板的斜边与另一个三角板的较长直角边平行,且直角顶点在较长直角边上,则图中( )
A.45° B.60° C.75° D.90°
二、填空题
6.一块直角三角板放在两平行直线上,如图所示,∠1+∠2= 度
7.如图,AB∥CD,直线l与AB,CD相交于点E,F,∠AEF=72°,点P是AB上一点,且PF平分∠EFC,过点P作PG⊥CD,交CD于点G,将△EPF沿射线EA方向平移,点F落在点F’处,若∠FPF’=3∠GPF’,则∠EPF’的度数为 .
8.如图1,是一种锂电池自动液压搬运物体叉车,图2是叉车侧面近似示意图.车身为四边形ABCD,,BC⊥AB,底座AB上装着两个半径为30cm的轮胎切于水平地面,AB=169cm,BC=120cm.挡货架AE上有一固定点T与AD的中点N之间由液压伸缩杆TN连接.当TN⊥AD时,TN的延长线恰好经过B点,则AD的长度是 cm;一个长方体物体准备装卸时,AE绕点A左右旋转,托物体的货叉PQ⊥AE(PQ沿着AE可上下滑动),PQ=65cm,AE=AD.当AE旋转至AF时,PQ下降到P'Q'的位置,此时F,D,C三点共线,且FQ'=52cm,则点P'到地面的离是 cm.
三、计算题
9.如图,在△ABC中,∠B=24°,∠ACB=104°,AD⊥BC于D,AE平分∠BAC,求∠DAE的度数.
10.如图,直线分别交直线于点G,H,射线分别在和的内部,且.
(1)若和互补.
①求的度数;
②当,且时,求的度数;
(2)设,.若,求m,n满足的等量关系.
四、解答题
11.如图,,且,连接,与相交于点O.求证:.
12.在中,M是斜边AB的中点,D为直线AB外一点,,连接AD,BD.
(1)如图1,若AD平分,求证:;
(2)如图2,若,,求AD的长;
(3)如图3,已知点D和边AC上的点E满足,.连接CD,求证:.
13.
已知I是的内心,AI的延长线交的外接圆于点D,连接DC,DB.
(1)在图1中:①证明:;②判断外心的位置,并证明;
(2)如图2,若AB为的外接圆直径,取AB中点O,且于点I,DE切圆O于点D,求的值.
五、综合题
14.如图,在 中,D是 边上的一点, , 平分 ,交 边于点E,连接 .
(1)求证: ;
(2)若 , ,求 的度数.
15.如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)如果AC=6cm,BC=8cm,试求△ACD的周长;
(2)如果∠CAD:∠BAD=1:2,求∠B的度数.
16.如图,二次函数的图象与x轴交于点和点B,与y轴交于点C,且顶点D的坐标为,对称轴与直线交于点E,与x轴交于点F,连接,.
(1)求二次函数的解析式;
(2)点P在上方二次函数图象上,且的面积等于6,求点P的坐标;
(3)在二次函数图象上是否存在一点M,使得?若存在,求出直线与x轴的交点Q的坐标;若不存在,请说明理由.
六、实践探究题
17.在物理学中,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
如图1,一束光线射到平面镜上,被反射后的光线为,则入射光线、反射光线与平面镜所夹的锐角.
(1)【简单应用】
如图2,有一口井,已知入射光线与水平线的夹角为,现放置平面镜,可使反射光线正好垂直照射到井底(即射线),与水平线的夹角的度数为 .
(2)【类比拓展】
如图3,有两块平面镜,且,入射光线经过两次反射,得到反射光线.由以上光的反射定律,可知入射角与反射角相等,进而可以推得他们的余角也相等,即:.在这样的条件下,求证:.
(3)【尝试探究】
两块平面镜,且,入射光线经过两次反射,得到反射光线.如图4,光线与相交于点,则的度数是多少?(用含的式子表示)(三角形内角和)
18.
(1)问题发现:
如图①,直线AB∥CD,连接BE,CE,可以发现∠B+∠C=∠BEC,请把下面的证明过程补充完整:
证明:过点E作EF∥AB,
∵AB∥DC(已知)
∴EF∥DC( ).
∴∠C=∠CEF.( ).
∵EF∥AB,
∴∠B=∠BEF (同理).
∴∠B+∠C= (等量代换),即∠B+∠C=∠BEC.
(2)拓展探究:
如果点E运动到图②所示的位置,其他条件不变,说明:∠B+∠C+∠BEC=360°.
(3)解决问题:如图③,AB∥DC,E、F、G是AB与CD之间的点,直接写出∠1,∠2,∠3,∠4,∠5之间的数量关系.
19. 综合实践.
我们发现平行线具有“等角转化”的功能,通过添加平行线可将不同位置的角“凑”在一起,得出角之间的关系.根据平行线的“等角转化”功能,解答下列问题:
(1)阅读理解:如图1,相交于点,请说明.阅读并补充下面推理过程.
解:如图1,过点作.
_▲_.
,
_▲_.
_▲_.
.
即.
(2)方法掌握:如图2,已知交于点.请写出之间的数量关系,并证明你的结论;
(3)拓展运用:如图3,已知,点在直线上,平分平分.若,求度数(用含的式子表示).
答案解析部分
1.【答案】C
【知识点】平行线的判定
2.【答案】D
【知识点】角的运算;平行线的性质
3.【答案】A
【知识点】平行线的性质
4.【答案】D
【知识点】余角、补角及其性质;平行线的判定与性质
5.【答案】C
【知识点】平行线的性质;三角形的外角性质
6.【答案】90
【知识点】平行线的性质;直角三角形的性质
7.【答案】108°
【知识点】平行线的性质;平移的性质;角平分线的定义
8.【答案】130;77
【知识点】平行线的判定与性质;三角形全等及其性质;勾股定理;锐角三角函数的定义
9.【答案】解:在△ABC中,
∵∠BAC+∠B+∠ACB=180°,∠B=24°,∠ACB=104°,
∴∠BAC=180°﹣∠B﹣∠ACB=180°﹣24°﹣104°=52°.
∵AE平分∠BAC,
∴∠EAC= ∠BAC= 52°=26°,
∵AD⊥BC,
∴∠ADC=90°,
∵∠ACB=104°,
∴∠ACD=180°﹣∠ACB=180°﹣104°=76°,
∴∠CAD=14°,
∴∠DAE=∠EAC+∠CAD=40°
【知识点】三角形内角和定理;三角形的外角性质
10.【答案】(1)解:①和互补,
.
,
,
;
②由①得,
,
,
又,
,
.
,
,
;
(2)解:,
.
设,
,,
,
,
又,
,
,
,
即m,n满足的等量关系为.
【知识点】角的运算;平行线的性质;邻补角
11.【答案】证明:,
,,
在与中,
,
.
【知识点】平行线的性质;三角形全等的判定(ASA)
12.【答案】(1)证明:如图,MD与BC交于点E,
∵AD平分,∴,
∵,∴,
∴,∴,
又∵是直角三角形,,
∴,∴;
(2)解:∵M是斜边AB的中点,,
∴,∴,,
在中,,
∴,
∵,,∴,
由勾股定理得:;
(3)证明:如图,延长BD、AC,交于点F,
则,
∵,,∴.
又∵,∴四边形BDEM是平行四边形.∴.
∵M是AB的中点,∴.
∴.∴四边形AMDE是平行四边形.
∵,∴平行四边形AMDE是菱形.∴.
∵,∴,,
∴,∴,
即点D是斜边的中点.∴.
【知识点】平行线的性质;勾股定理;平行四边形的判定;菱形的判定;三角形全等的判定(ASA);角平分线的定义;直角三角形斜边上的中线
13.【答案】(1)解:①
∵I是的内心
∴AI平分,
∴
②D为外心,证明如下:
∵I是的内心
∴BI平分,,∵,
∴
∴,即
∴D为外心
(2)解:连接OD
∵AB为的外接圆直径,O为AB中点
∴O为的外接圆圆心
∵DE切圆O于点D
∴,即,
∵,∴,
∵AB为的外接圆直径
∴,∴,
∵,,∴
∵由(1)得,∴
∴
【知识点】圆周角定理;三角形的外接圆与外心;解直角三角形
14.【答案】(1)证明: 平分 ,
,
在 和 中, ,
;
(2)解: , ,
,
平分 ,
,
在 中, .
【知识点】三角形内角和定理;三角形全等的判定(SAS);角平分线的定义
15.【答案】(1)由折叠的性质可知,DE垂直平分线段AB,
根据垂直平分线的性质可得:DA=DB,
所以,DA+DC+AC=DB+DC+AC=BC+AC=14cm;
(2)设∠CAD=x,则∠BAD=2x,
∵DA=DB,
∴∠B=∠BAD=2x,
在Rt△ABC中,∠B+∠BAC=90°,
即:2x+2x+x=90°,x=18°,
∠B=2x=36°.
【知识点】角的运算;余角、补角及其性质;线段垂直平分线的性质;轴对称的性质;翻折变换(折叠问题)
16.【答案】(1)解:设二次函数的解析式为设二次函数的解析式为y=a(x﹣h)2+k
把顶点D(﹣2,8)代入,得
y= a(x +2)2+8.把点(﹣6,0)代入得:
0= a(﹣6+2)2+8.
∴ a =﹣
∴二次函数的解析式为y=﹣(x +2)2+8;
(2)解:∵y=﹣(x +2)2+8=﹣x2﹣2x+6
∴C(0,6),
设直线AC的解析式为y=kx+b,把A,C的坐标代入,得
解得:
直线AC的解析式为y=x+6,
∵二次函数的对称轴是直线,
∴E点的横坐标是-2
∴
∴
∴
∴DE=4,
∴
∴h=3,
∴P点的横坐标为-5,
∴
∴
(3)解:存在
∵A(﹣6,0) ,C(0,6)
∴ OA=OC=6
∴△ AOC为等腰直角三角形,
∴∠ ACO= 45°
令y=0
0=﹣x2﹣2x+6
解得:x1=2,x2=﹣6
∴点B(2,0)
①当CM在∠ ACO内部时,如图
∵∠ACM + ∠OCB=45°,∠ACM+∠MCO=∠ ACO= 45°
∴∠OCB=∠MCO
∴OQ=OB=2
∴点Q(﹣2,0)
②当CM在∠ ACO外部时,如图:
∵∠ACM + ∠OCB=45°,∠ ACO= 45°
∴∠BCQ=90°
设点Q(t,0)
则BQ=2- t
CQ2=OC2+OQ2= t 2+62
BC2=OB2+OC2=22+62
∵BQ2= CQ2+ BC2
∴(2﹣ t)2= t 2+62+22+62
t =﹣18
综上所述,直线CM与x轴的交点Q的坐标为(﹣2,0)或(﹣18,0).
【知识点】待定系数法求二次函数解析式;三角形的面积;勾股定理;等腰直角三角形;二次函数图象上点的坐标特征
17.【答案】(1)65°
(2)解:如图1,∵OM⊥ON,
∴∠CON=90°,
∴∠2+∠3=90°,
∵∠1=∠2,∠3=∠4,
∴∠1+∠2+∠3+∠4=180°,
∠DCB+∠ABC=180°,
AB∥CD;
(3)解:如图4,在△OBC中,
∵∠MON=α,
∴∠2+∠3=180°﹣α,
∵∠1=∠2,∠3=∠4,
∴
∴∠BEC=180°﹣∠ABC﹣∠BCD
=180°﹣(180°﹣2∠2)﹣(180°﹣2∠3)
=2(∠2+∠3)﹣180°
=2(180°﹣a)﹣180°
=180°﹣2α,
故答案为:180°﹣2α;
【知识点】垂线;平行线的性质
18.【答案】(1)平行于同一直线的两直线平行;两直线平行,内错角相等;∠BEF+∠CEF
(2)解:如图②,过点E作EF∥AB,
∵AB∥CD,EF∥AB,
∴EF∥CD,
∴∠C+∠CEF=180°,∠B+∠BEF=180°,
∴∠B+∠C+∠BEC=360°,
∴∠B+∠C=360°﹣(∠BEF+∠CEF),
即∠B+∠C+∠BEC=360°;
(3)解:∠1+∠3+∠5=∠2+∠4,理由如下:
如图,过点F作FM∥AB,则AB∥FM∥CD,
由(1)得,∠1+∠3+∠5=∠2+∠4.
【知识点】平行公理及推论;平行线的判定与性质
19.【答案】(1)解:如图1,过点P作,
∴
∵
∴
∴
∴
即
(2)解:,理由如下:
过点M作,如图2:
∴,
∵
∴
∴
∵
∴
∴
即
(3)解:,理由如下:
∵平分平分
∴
∵
∴
∵,
∴
∴
即
【知识点】平行公理及推论;平行线的性质;三角形内角和定理;角平分线的定义
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
