2023-2024学年重庆市凤鸣山中学高一(下)月考物理试卷(5月)(含解析)
文档属性
| 名称 | 2023-2024学年重庆市凤鸣山中学高一(下)月考物理试卷(5月)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-06-09 17:23:16 | ||
图片预览




文档简介
2023-2024学年重庆市凤鸣山中学高一(下)月考物理试卷(5月)
一、单选题:本大题共8小题,共32分。
1.关于做曲线运动的物体,下列说法正确的是( )
A. 其速度可以保持不变 B. 其动能一定发生变化
C. 它所受的合外力一定是变力 D. 它所受的合外力一定不为零
2.关于摩擦力做功的下列说法中正确的是( )
A. 滑动摩擦力阻碍物体的相对运动,一定做负功
B. 静摩擦力有阻碍物体的相对运动趋势的作用,一定不做功
C. 静摩擦力和滑动摩擦力一定都做负功
D. 系统内两物体间相互作用,一对摩擦力做功的总和不一定等于零
3.如图甲拳击训练时,训练师拿着厚厚的防护垫以延长接触时间避免自己受伤:铁砂掌大师在表演“手劈砖头”时,往往减少手与砖接触时间才能完成挑战,如图乙。下列说法正确的是( )
A. 拳击训练师是为了减小拳手对自己的冲量 B. 拳击训练师是为了减小拳手对自己的冲力
C. 铁砂掌大师是为了减小手对砖头的作用力 D. 铁砂掌大师是为了减小手对砖头的冲量
4.质量为的汽车,启动后沿平直路面行驶,如果发动机的功率恒为,且行驶过程中受到摩擦阻力大小一定,汽车速度能够达到的最大值为,那么当汽车的车速为时,汽车的瞬时加速度的大小为( )
A. B. C. D.
5.一质量为的小球以初动能竖直向上抛出,小球上升的最大高度为,小球在运动过程中阻力大小恒为,则小球从被抛出至落回出发点的过程中( )
A. 重力做功为 B. 小球所受合力做功为
C. 阻力做功为 D. 落回出发点时动能为
6.如图为某双星系统、绕其连线上的点做匀速圆周运动的示意图,若星的轨道半径大于星的轨道半径,双星的总质量为,双星间的距离为,其运动周期为,则
A. 的质量一定大于的质量 B. 的线速度一定大于的线速度
C. 一定,越大,越大 D. 一定,越大,越小
7.年月日,如图所示,神舟十三号载人飞船返回舱在东风着陆场预定区域成功着陆。三名航天员结束为期个月的太空“出差”,回到地球的怀抱。返回舱在距地面高左右时,相对地面竖直向下的速度为,此时反推发动机点火,在极短时间内喷出体积为的气体、其速度相对地面竖直向下为,能使返回舱平稳落地。已知喷出气体的密度为,估算返回舱受到的平均反冲力大小为( )
A. B. C. D.
8.如图甲所示,足够长的水平传送带以恒定的速度匀速运动。时刻在适当的位置放上质量为、具有一定初速度的小物块,小物块在传送带上运动的图像如图乙所示,以传送带运动的方向为正方向,已知物块与传送带间的动摩擦因数为,,,,重力加速度为,下列说法正确的( )
A. 内小物块加速度先减小后增大
B. 小物块在内位移是内的位移的倍
C. ,摩擦力对物块做的功为
D. ,物块与传送带间产生的热量为
二、多选题:本大题共4小题,共16分。
9.质量为的探月航天器在接近月球表面的轨道上飞行,其运动视为匀速圆周运动。已知月球的质量为,月球的半径为,月球表面的重力加速度为,引力常量为,不考虑月球自转的影响,则关于航天器( )
A. 运行周期 B. 线速度
C. 加速度 D. 角速度
10.如图所示,质量为的钢球以速度水平射入静止于光滑水平面上的弹簧枪的枪管中,弹簧枪的质量为。钢球在枪管内压缩弹簧至最大压缩量过程中,下列说法正确的是( )
A. 系统机械能守恒,动量不守恒
B. 钢球动能先增大后减小
C. 弹簧压缩量最大时,弹簧枪的速度为
D. 弹簧压缩量最大时,弹性势能为
11.如图所示,在匀速转动的水平圆盘上,沿直径方向放着用轻绳相连的物体和,和质量都为。它们分居圆心两侧,与圆心的距离分别为,,
A. 与盘间的动摩擦因数相同且均为。若最大静摩擦力等于滑动摩擦力,当圆盘转速加快到两物体刚好还未发生滑动时,下列说法正确的是( ) A.绳子张力为
B. 圆盘的角速度为
C. 此时所受摩擦力方向沿绳指向圆外
D. 烧断绳子,物体、仍将随盘一块转动
12.如图甲所示为建筑工地重器塔吊。工作时悬臂保持不动,可沿悬臂水平移动的天车下有一个挂钩可用于悬挂重物。天车有两个功能,一是吊着重物沿竖直方向运动,二是吊着重物沿水平方向运动。重物经过点开始计时,在将一质量为的重物运送到过程中,天车水平方向以的速度匀速运动,竖直方向运动的加速度随时间变化如图乙所示,不计一切阻力,重力加速度为,对于该过程,下列说法正确的是( )
A. 重物做匀变速曲线运动,合力竖直向下
B. 在与时刻,拉线对重物拉力的差值为
C. 时刻,重物的动能大小为
D. ,拉线对重物拉力的冲量大小为
三、实验题:本大题共2小题,共18分。
13.某同学验证两个小球在斜槽末端碰撞时的动量守恒,实验装置如图所示。、为两个直径相同的小球。实验时,不放,让从固定的斜槽上点自由滚下,在水平面上得到一个落点位置;将放置在斜槽末端,让再次从斜槽上点自由滚下,与发生正碰,在水平面上又得到两个落点位置。三个落点位置标记为、、。
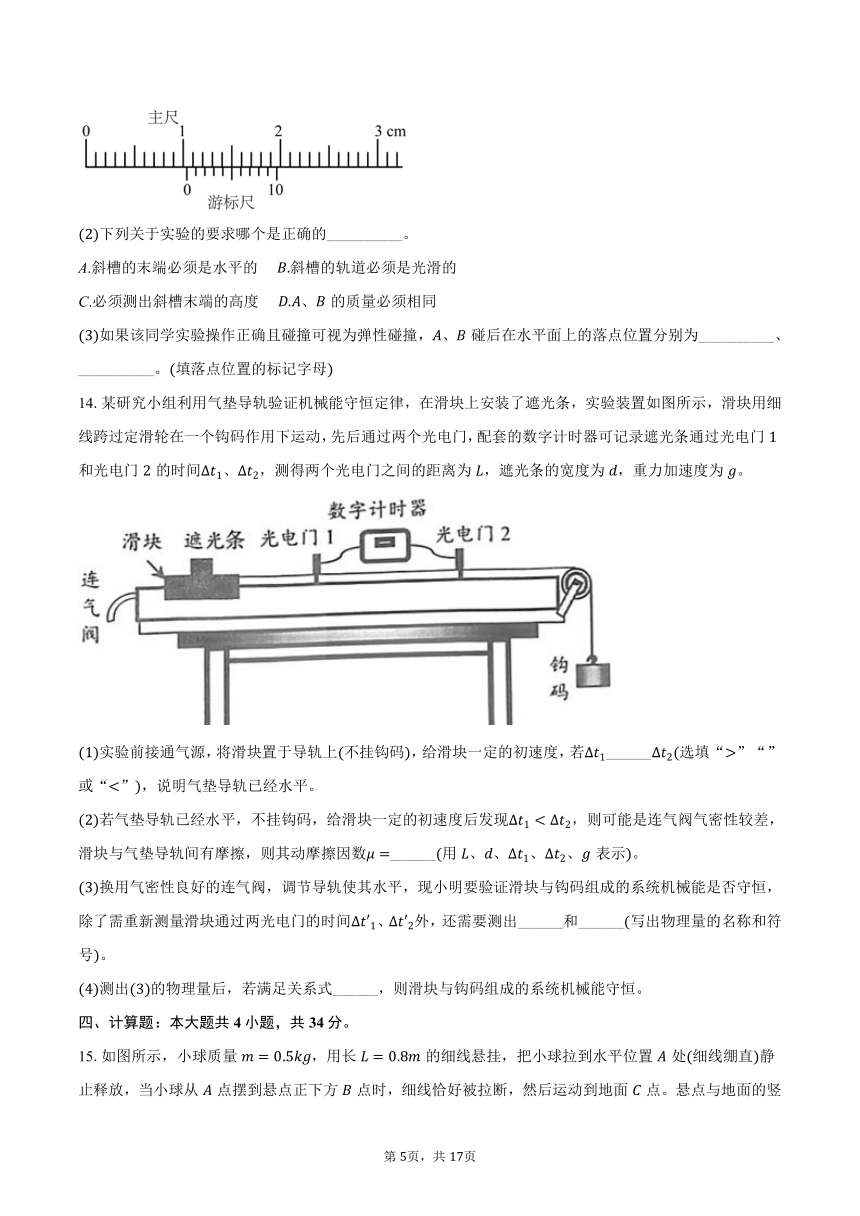
为了确认两个小球的直径相同,该同学用分度的游标卡尺对它们的直径进行了测量,某次测量的结果如下图所示,其读数为__________。
下列关于实验的要求哪个是正确的__________。
A.斜槽的末端必须是水平的 斜槽的轨道必须是光滑的
C.必须测出斜槽末端的高度 、的质量必须相同
如果该同学实验操作正确且碰撞可视为弹性碰撞,、碰后在水平面上的落点位置分别为__________、__________。填落点位置的标记字母
14.某研究小组利用气垫导轨验证机械能守恒定律,在滑块上安装了遮光条,实验装置如图所示,滑块用细线跨过定滑轮在一个钩码作用下运动,先后通过两个光电门,配套的数字计时器可记录遮光条通过光电门和光电门的时间、,测得两个光电门之间的距离为,遮光条的宽度为,重力加速度为。
实验前接通气源,将滑块置于导轨上不挂钩码,给滑块一定的初速度,若______选填“”“”或“”,说明气垫导轨已经水平。
若气垫导轨已经水平,不挂钩码,给滑块一定的初速度后发现,则可能是连气阀气密性较差,滑块与气垫导轨间有摩擦,则其动摩擦因数______用、、、、表示。
换用气密性良好的连气阀,调节导轨使其水平,现小明要验证滑块与钩码组成的系统机械能是否守恒,除了需重新测量滑块通过两光电门的时间、外,还需要测出______和______写出物理量的名称和符号。
测出的物理量后,若满足关系式______,则滑块与钩码组成的系统机械能守恒。
四、计算题:本大题共4小题,共34分。
15.如图所示,小球质量,用长的细线悬挂,把小球拉到水平位置处细线绷直静止释放,当小球从点摆到悬点正下方点时,细线恰好被拉断,然后运动到地面点。悬点与地面的竖直高度,不计空气阻力,取。求:
小球从到重力势能的减少量;
小球运动到点时的速度大小;
小球落地点与的水平距离。
16.开普勒第三定律指出:所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等。该定律对一切具有中心天体的引力系统都成立。如图,嫦娥三号探月卫星在半径为的圆形轨道Ⅰ上绕月球运行,周期为。月球的半径为,引力常量为。某时刻嫦娥三号卫星在点变轨进入椭圆轨道Ⅱ,在月球表面的点着陆。、、三点在一条直线上。求:
月球的密度;
在轨道Ⅱ上运行的时间。
17.保龄球又称“地滚球”,是一种在木板球道上用球滚击球瓶的室内体育运动。一位保龄球手在练习投掷时,在投球区投出一颗质量的球,如图所示,该球在点以的初速度沿直线运动,并与静止在点的质量的球瓶相撞。球可视为沿直线撞出且速度共线。已知,滚球与轨道间的摩擦力恒为重力的倍,、均可看成质点。取。求:
球在撞上球前瞬间的速度大小;
若撞击后、速度均向右,且大小之比为,碰撞过程中、系统损失的动能;
若换用质量满足的球撞击球瓶,可视为弹性正碰,球瓶获得的速度。
18.如图甲所示为年北京冬奥会上,我国滑雪运动员谷爱凌女子大跳台夺冠瞬间。图乙是女子大跳台完整结构示意图,是助滑坡段,高度;圆弧为起飞段,圆心角,半径,与圆弧相切;为着陆坡段,高度,倾角;为停止区。某次运动员从点由静止开始自由起滑,经过圆弧从与点等高的点飞出,最终恰好沿面从点落入着陆坡段,与圆弧相切于。已知除圆弧轨道外,其余轨道各部分与滑雪板间的动摩擦因数均为,经过圆弧段对点压力为重力的倍,运动员连同滑雪板的质量,各段连接处无能量损失,忽略空气阻力的影响。取,,。求:
运动员在点的速度大小;
运动员经过圆弧段时摩擦力做的功;
运动员在停止区运动的时间为多少?
答案和解析
1.【答案】
【解析】解:、曲线运动的速度沿轨迹上各点的切线方向,所以做曲线运动的物体其速度方向一定变化,则速度一定变化,故A错误;
B、做曲线运动的物体其速度大小可能不变,即动能可能不变,例如匀速圆周运动,故B错误;
C、做曲线运动的物体它所受的合外力可能是恒力,例如平抛运动,故C错误;
D、做曲线运动的物体速度一定变化,则加速度一定不为零,则它所受的合外力一定不为零,故D正确。
故选:。
曲线运动的条件的是合外力与速度不一条直线上,速度方向时刻变化,故曲线运动是变速运动.曲线运动合力一定不能为零。
本题主要考查了曲线运动的条件,解题关键是掌握曲线运动的条件,合外力与速度不一条直线上,知道曲线运动合外力一定不为零,速度方向时刻变化,一定是变速运动。
2.【答案】
【解析】解:、恒力做功的表达式,滑动摩擦力的方向与物体相对运动方向相反,但与运动方向可以相同,也可以相反,物体受滑动摩擦力也有可能位移为零,故可能做负功,也可能做正功,也可以不做功,故A错误;
B、恒力做功的表达式,静摩擦力的方向与物体相对运动趋势方向相反,但与运动方向可以相同,也可以相反,还可以与运动方向垂直,故静摩擦力可以做正功,也可以做负功,也可以不做功,故BC错误,
D、一对相互作用的滑动摩擦力大小相等,方向相反,作用的两个物体位移不同,伴随机械能的损耗转化为内能,所以一对滑动摩擦力做功的总和恒为负值,故D正确;
故选:
功等于力与力的方向上的位移的乘积,这里的位移是相对于参考系的位移;静摩擦力的方向与物体的相对运动趋势方向想法,滑动摩擦力的方向与物体的相对滑动的方向相反.
本题关键要分清相对运动方向与运动方向的关系,前者是相对与与物体接触的另一个物体,而后者是相对与参考系;同时要明确恒力做功的求法.
3.【答案】
【解析】解:,拳击训练时拳头对人的冲量是不变的,根据动量定理可知,带上厚厚的防护垫是增加接触时间,为了减小拳手对自己的冲力,故A错误,B正确;
,练铁砂掌时手对砖头的冲量是不变的,根据动量定理,可知,减少手与砖接触时间从而增加手对砖头的作用力,故CD错误。
故选:。
根据动量定理,动量变化一定时,作用时间越短,作用力就越大,作用时间越长,作用力就越小。
本题考查了对动量定理的理解和应用,要知道动量变化一定时,作用时间与作用力大小成反比。
4.【答案】
【解析】【分析】该题考查汽车恒定功率启动相关知识。分析好物理情景,灵活应用公式是解决本题的关键。
当汽车匀速行驶时,有,由此求解,再根据汽车功率恒定,求解汽车的车速为时的牵引力,最后应用牛顿第二定律求解瞬时加速度的大小。
【解答】
当汽车匀速行驶时,有.
根据,得,
由牛顿第二定律得故B正确,、、D错误
故选B
5.【答案】
【解析】解:,小球从被抛出至落回出发点的过程中,重力的位移为零,则重力做功为零,故A错误;
,小球所受阻力做功为,则合力做功为,故B正确,C错误;
,由能量关系可知,落回出发点时动能为,故D错误。
故选:。
除重力以外的其它力对小球做的功等于小球机械能的变化量,根据功的计算公式分析阻力做的功,由此分析机械能的变化量。
本题主要是考查了功的计算方法和动能定理的应用,明确合外力的总功等于动能的变化。
6.【答案】
【解析】解:、设双星质量分别为、,轨道半径分别为、,角速度相等,均为,根据万有引力定律可知:,距离关系为:,联立解得:,因为,所以的质量一定小于的质量,故A错误;
B、根据线速度与角速度的关系有:、,因为角速度相等,半径,所以的线速度大于的线速度,故B正确;
、周期,由选项可得周期为:,总质量一定,两星间距离越大,周期越大,一定,越大,越小,故CD错误。
故选:。
双星靠相互间的万有引力提供向心力,具有相同的角速度,根据牛顿第二定律列式得到周期表达式进行分析。
此题考查了万有引力定律及其应用,解决本题的关键知道双星靠相互间的万有引力提供向心力,具有相同的角速度。以及会用万有引力提供向心力进行求解。
7.【答案】
【解析】喷出气体的质量为
以喷出气体为研究对象,设气体受到的平均冲力为 ,以向下为正方向,根据动量定理可得
由于在极短时间 内喷出气体,可认为喷出气体的重力冲量忽略不计,故有
解得
根据牛顿第三定律可知返回舱受到的平均反冲力大小为 ,A正确,BCD错误。
故选A。
8.【答案】
【解析】解:、根据图像斜率的物理意义,可知内图像的斜率不变,则小物块加速度不变,故A错误;
,因图像的“面积”等于位移,结合题意,,,可知小物块在内位移是内的位移的倍,故B错误;
,根据求功公式,可知,摩擦力对物块做的功为:,故C正确;
,结合图象,可得,物块相对传送带的位移为:,则物块与传送带间产生的热量为:,故D错误。
故选:。
根据图像斜率的物理意义判断;根据图象与时间轴所围的面积来分析物块的位移关系;根据求功公式求解内摩擦力对物块做功;结合图象,求得,物块相对传送带的位移,再根据公式求解产生的热量。
本题考查了倾斜传送带问题,解决此题的关键是根据图象要能分析出物块的运动情况,再判断其受力情况,灵活应用图象面积的物理意义。
9.【答案】
【解析】解:,在地表附近万有引力等于重力:
探月航天器在接近月球表面的轨道上飞行,则轨道半径为,根据万有引力提供卫星做圆周运动的向心力,则
解得航天器运行周期:
故A正确;
,根据万有引力提供卫星做圆周运动的向心力,则
解得航天器线速度
故B正确;
,根据万有引力提供卫星做圆周运动的向心力,则
解得航天器加速度
故C错误;
,根据万有引力提供卫星做圆周运动的向心力,则
解得航天器角速度
故D错误。
故选:。
探月航天器绕月球做匀速圆周运动,根据万有引力提供向心力,列出等式,可求线速度、角速度、周期和向心加速度。不考虑月球自转的影响,万有引力等于重力。
解决本题的关键要掌握万有引力定律应用的两条基本思路:万有引力等于向心力和万有引力等于重力,要掌描述圆周运动的各个量之间的关系,并能灵活运用。
10.【答案】
【解析】解:,钢球与弹簧枪除受重力外所受的支持力不做功,所以系统机械能守恒;系统所受合外力为零,所以系统动量守恒,故A错误;
,钢球在枪管内压缩弹簧至最大压缩量过程,钢球速度逐渐减小,弹簧枪速度逐渐增大,最大压缩量时,二者有共同速度,所以钢球动能逐渐减小,故B错误;
,弹簧压缩量最大时,规定向左为正方向,由动量守恒定律得
解得弹簧枪和钢球的共同速度为
故C正确;
,由机械能守恒可得,弹簧压缩量最大时,根据能量守恒定律可知弹性势能为:
故D正确。
故选:。
小球与弹簧接触后,根据机械能守恒定律与能量守恒定律的条件分析;根据能量守恒定律结合动量守恒定律解得。
解决本题的关键会根据小球的受力,运用牛顿第二定律,判断机械能与动量是否守恒。
11.【答案】
【解析】C.两物体和随着圆盘转动时,合力提供向心力,有
的轨道半径比的轨道半径大,所以所需向心力大,绳子拉力相等,所以当圆盘转速加快到两物体刚好还未发生滑动时,所受的最大静摩擦力方向沿绳指向圆心,所受的最大静摩擦力方向沿绳背离圆心,故C正确;
设绳子拉力为,以为研究对象,有
以为研究对象有
联立解得
故A正确,B错误;
D.烧断绳子,对分析,若恰好未发生相对滑动有
解得
故此时烧断绳子一定发生相对滑动,同理可得,也一定发生相对滑动,故D错误。
故选AC。
12.【答案】
【解析】解:,依题意可知,重物竖直方向做加速度随时间均匀减小的加速运动,所以重物合力竖直向上,做非匀变速曲线运动,故A错误;
,在时刻,根据牛顿第二定律,由图乙可得
时刻,重物加速度为,拉线对重物拉力
二者的差值为
联立解得:
故B正确;
,根据图像围成的面积表示速度的改变量,可得时刻,重物在竖直方向上的速度大小为
则时刻,重物的速度大小为
根据动能的公式有
故C错误;
,对重物,根据动量定理可得
解得:
故D正确。
故选:。
由于加速度在变化,所以重物做非匀变速曲线运动,根据牛顿第二定律解得;图像围成的面积表示速度的改变量,结合动量定理解答。
本题考查动量定理,解题关键掌握重物运动状态的分析,结合动量定理与牛顿第二定律解答。
13.【答案】;
;
;
【解析】观察主尺的单位为 ,读出主尺的读数是 ,游标尺上的第五条刻度线与主尺上的刻度线对齐,其读数为 ,结合主尺及游标尺的读数得到被测直径为
首先考查在实验的过程中,需要小球两次沿斜槽滚到末端时的速度都水平且大小相同。实验时应使小球每次都从同一位置由静止开始释放,并不需要斜槽的轨道光滑的条件,也不需要测出斜槽末端的高度,但是必须保证斜槽末端水平,故A正确,BC错误;
D.小球与发生正碰时,为使小球在碰后不反弹,要求小球的质量大于小球的质量,故D错误。
故选A。
设、两球的质量分别为和,且;碰前的速度;因为两个金属小球的碰撞视为弹性碰撞,则由动量守恒定律得
由机械能守恒定律得
解得 ,
可见碰后小球的速度小于小球的速度,也小于碰前的速度;所以小球单独滚下落到水平面上的位置为,、碰后在水平面上的落点位置分别为、。
14.【答案】 钩码质量 滑块质量
【解析】解:实验前接通气源,将滑块置于导轨上不挂钩码,给滑块一定的初速度,若,可认为滑块做匀速运动,说明气垫导轨已经水平;
由于挡光时间很短,滑块经过两个光电门时的速度可认为等于挡光过程的平均速度,则有,,滑块从光电门到光电门过程,根据动能定理可得,联立解得;
要验证滑块与钩码组成的系统机械能是否守恒,需要知道钩码减少的重力势能和钩码、滑块增加的动能,故除了需重新测量滑块通过两光电门的时间、外,还需要测出钩码的质量和滑块的质量;
钩码减少的重力势能为,钩码、滑块增加的动能为,若满足关系式则滑块与钩码组成的系统机械能守恒;
故答案为:;;钩码质量;滑块质量;。
实验前接通气源,将滑块置于导轨上不挂钩码,给滑块一定的初速度,若,可认为滑块做匀速运动,说明气垫导轨已经水平;根据挡光时间很短,滑块经过两个光电门时的速度可认为等于挡光过程的平均速度求解;要验证滑块与钩码组成的系统机械能是否守恒,需要知道钩码减少的重力势能和钩码、滑块增加的动能,故除了需重新测量滑块通过两光电门的时间、外,还需要测出钩码的质量和滑块的质量;钩码减少的重力势能和钩码、滑块增加的动能相等则系统机械能守恒。
本题考查了验证机械能守恒定律的实验,熟练掌握实验原理是解题关键,学生需熟练掌握实验原理、误差分析并能应用机械能守恒定律解题。
15.【答案】解:小球从到重力势能的减少量为
小球从到过程,根据机械能守恒定律可得
解得小球运动到点时的速度大小为
小球从到做平抛运动,竖直方向有
解得
代入数据解得:
小球落地点与的水平距离为
答:小球从到重力势能的减少量为;
小球运动到点时的速度大小为;
小球落地点与的水平距离为。
【解析】根据重力做功可表示重力势能的减少.
根据动能定理可解得
根据平抛运动规律可解得水平距离.
本题考查了圆周运动和平抛运动的综合运用,知道圆周运动向心力的来源和平抛运动在水平方向和竖直方向上的运动规律是解决本题的关键.
16.【答案】解:由万有引力充当向心力:,
解得
月球的密度:,解得。
椭圆轨道的半长轴:,
设椭圆轨道上运行周期为,
由开普勒第三定律有:,
在轨道Ⅱ上运行的时间为,
解得。
【解析】根据万有引力提供向心力,结合卫星的轨道半径和周期求出月球的质量,根据月球的体积求出月球的密度;
根据几何关系求出椭圆轨道的半长轴,结合开普勒第三定律求出在轨道上运行的时间。
本题考查了万有引力定律和开普勒第三定律的综合运用,知道在Ⅱ轨道上运行的时间等于椭圆轨道运动周期的一半,结合开普勒第三定律进行求解。
17.【答案】 ; ;
【解析】保龄球从点到点由动能定理得
解得球在撞上球前瞬间的速度大小
撞击后、速度大小分别为 、 ,由动量守恒定律可得
解得
则碰撞过程中、系统损失的动能为
由动量守恒定律和机械能守恒定律得
,
解得
由于 ,所以
18.【答案】解:运动员在点,由牛顿第二定律可得
则
解得运动员在点的速度大小
从点到点由动能定理得
代入数据解得
点与点的高度差为
从点到点由动能定理得
又
代入数据解得
运动员经过圆弧段时由动能定理得
解得运动员经过圆弧段时摩擦力做的功
从点到点由动能定理得
代入数据解得
在段由牛顿第二定律得
则运动员在停止区运动的时间为
答:运动员在点的速度大小为;
运动员经过圆弧段时摩擦力做的功为;
运动员在停止区运动的时间为。
【解析】运动员做圆周运动,根据向心力计算在点的速度大小;
从点到点由动能定理计算速度大小,在圆弧段时由动能定理计算摩擦力做的功;
从点到点由动能定理计算末速度大小,再计算时间。
本题考查了动能定理与圆周运动和平抛运动的综合运用,熟练掌握平抛运动在水平方向和竖直方向上的运动规律是解决本题的关键。
第1页,共1页
一、单选题:本大题共8小题,共32分。
1.关于做曲线运动的物体,下列说法正确的是( )
A. 其速度可以保持不变 B. 其动能一定发生变化
C. 它所受的合外力一定是变力 D. 它所受的合外力一定不为零
2.关于摩擦力做功的下列说法中正确的是( )
A. 滑动摩擦力阻碍物体的相对运动,一定做负功
B. 静摩擦力有阻碍物体的相对运动趋势的作用,一定不做功
C. 静摩擦力和滑动摩擦力一定都做负功
D. 系统内两物体间相互作用,一对摩擦力做功的总和不一定等于零
3.如图甲拳击训练时,训练师拿着厚厚的防护垫以延长接触时间避免自己受伤:铁砂掌大师在表演“手劈砖头”时,往往减少手与砖接触时间才能完成挑战,如图乙。下列说法正确的是( )
A. 拳击训练师是为了减小拳手对自己的冲量 B. 拳击训练师是为了减小拳手对自己的冲力
C. 铁砂掌大师是为了减小手对砖头的作用力 D. 铁砂掌大师是为了减小手对砖头的冲量
4.质量为的汽车,启动后沿平直路面行驶,如果发动机的功率恒为,且行驶过程中受到摩擦阻力大小一定,汽车速度能够达到的最大值为,那么当汽车的车速为时,汽车的瞬时加速度的大小为( )
A. B. C. D.
5.一质量为的小球以初动能竖直向上抛出,小球上升的最大高度为,小球在运动过程中阻力大小恒为,则小球从被抛出至落回出发点的过程中( )
A. 重力做功为 B. 小球所受合力做功为
C. 阻力做功为 D. 落回出发点时动能为
6.如图为某双星系统、绕其连线上的点做匀速圆周运动的示意图,若星的轨道半径大于星的轨道半径,双星的总质量为,双星间的距离为,其运动周期为,则
A. 的质量一定大于的质量 B. 的线速度一定大于的线速度
C. 一定,越大,越大 D. 一定,越大,越小
7.年月日,如图所示,神舟十三号载人飞船返回舱在东风着陆场预定区域成功着陆。三名航天员结束为期个月的太空“出差”,回到地球的怀抱。返回舱在距地面高左右时,相对地面竖直向下的速度为,此时反推发动机点火,在极短时间内喷出体积为的气体、其速度相对地面竖直向下为,能使返回舱平稳落地。已知喷出气体的密度为,估算返回舱受到的平均反冲力大小为( )
A. B. C. D.
8.如图甲所示,足够长的水平传送带以恒定的速度匀速运动。时刻在适当的位置放上质量为、具有一定初速度的小物块,小物块在传送带上运动的图像如图乙所示,以传送带运动的方向为正方向,已知物块与传送带间的动摩擦因数为,,,,重力加速度为,下列说法正确的( )
A. 内小物块加速度先减小后增大
B. 小物块在内位移是内的位移的倍
C. ,摩擦力对物块做的功为
D. ,物块与传送带间产生的热量为
二、多选题:本大题共4小题,共16分。
9.质量为的探月航天器在接近月球表面的轨道上飞行,其运动视为匀速圆周运动。已知月球的质量为,月球的半径为,月球表面的重力加速度为,引力常量为,不考虑月球自转的影响,则关于航天器( )
A. 运行周期 B. 线速度
C. 加速度 D. 角速度
10.如图所示,质量为的钢球以速度水平射入静止于光滑水平面上的弹簧枪的枪管中,弹簧枪的质量为。钢球在枪管内压缩弹簧至最大压缩量过程中,下列说法正确的是( )
A. 系统机械能守恒,动量不守恒
B. 钢球动能先增大后减小
C. 弹簧压缩量最大时,弹簧枪的速度为
D. 弹簧压缩量最大时,弹性势能为
11.如图所示,在匀速转动的水平圆盘上,沿直径方向放着用轻绳相连的物体和,和质量都为。它们分居圆心两侧,与圆心的距离分别为,,
A. 与盘间的动摩擦因数相同且均为。若最大静摩擦力等于滑动摩擦力,当圆盘转速加快到两物体刚好还未发生滑动时,下列说法正确的是( ) A.绳子张力为
B. 圆盘的角速度为
C. 此时所受摩擦力方向沿绳指向圆外
D. 烧断绳子,物体、仍将随盘一块转动
12.如图甲所示为建筑工地重器塔吊。工作时悬臂保持不动,可沿悬臂水平移动的天车下有一个挂钩可用于悬挂重物。天车有两个功能,一是吊着重物沿竖直方向运动,二是吊着重物沿水平方向运动。重物经过点开始计时,在将一质量为的重物运送到过程中,天车水平方向以的速度匀速运动,竖直方向运动的加速度随时间变化如图乙所示,不计一切阻力,重力加速度为,对于该过程,下列说法正确的是( )
A. 重物做匀变速曲线运动,合力竖直向下
B. 在与时刻,拉线对重物拉力的差值为
C. 时刻,重物的动能大小为
D. ,拉线对重物拉力的冲量大小为
三、实验题:本大题共2小题,共18分。
13.某同学验证两个小球在斜槽末端碰撞时的动量守恒,实验装置如图所示。、为两个直径相同的小球。实验时,不放,让从固定的斜槽上点自由滚下,在水平面上得到一个落点位置;将放置在斜槽末端,让再次从斜槽上点自由滚下,与发生正碰,在水平面上又得到两个落点位置。三个落点位置标记为、、。
为了确认两个小球的直径相同,该同学用分度的游标卡尺对它们的直径进行了测量,某次测量的结果如下图所示,其读数为__________。
下列关于实验的要求哪个是正确的__________。
A.斜槽的末端必须是水平的 斜槽的轨道必须是光滑的
C.必须测出斜槽末端的高度 、的质量必须相同
如果该同学实验操作正确且碰撞可视为弹性碰撞,、碰后在水平面上的落点位置分别为__________、__________。填落点位置的标记字母
14.某研究小组利用气垫导轨验证机械能守恒定律,在滑块上安装了遮光条,实验装置如图所示,滑块用细线跨过定滑轮在一个钩码作用下运动,先后通过两个光电门,配套的数字计时器可记录遮光条通过光电门和光电门的时间、,测得两个光电门之间的距离为,遮光条的宽度为,重力加速度为。
实验前接通气源,将滑块置于导轨上不挂钩码,给滑块一定的初速度,若______选填“”“”或“”,说明气垫导轨已经水平。
若气垫导轨已经水平,不挂钩码,给滑块一定的初速度后发现,则可能是连气阀气密性较差,滑块与气垫导轨间有摩擦,则其动摩擦因数______用、、、、表示。
换用气密性良好的连气阀,调节导轨使其水平,现小明要验证滑块与钩码组成的系统机械能是否守恒,除了需重新测量滑块通过两光电门的时间、外,还需要测出______和______写出物理量的名称和符号。
测出的物理量后,若满足关系式______,则滑块与钩码组成的系统机械能守恒。
四、计算题:本大题共4小题,共34分。
15.如图所示,小球质量,用长的细线悬挂,把小球拉到水平位置处细线绷直静止释放,当小球从点摆到悬点正下方点时,细线恰好被拉断,然后运动到地面点。悬点与地面的竖直高度,不计空气阻力,取。求:
小球从到重力势能的减少量;
小球运动到点时的速度大小;
小球落地点与的水平距离。
16.开普勒第三定律指出:所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等。该定律对一切具有中心天体的引力系统都成立。如图,嫦娥三号探月卫星在半径为的圆形轨道Ⅰ上绕月球运行,周期为。月球的半径为,引力常量为。某时刻嫦娥三号卫星在点变轨进入椭圆轨道Ⅱ,在月球表面的点着陆。、、三点在一条直线上。求:
月球的密度;
在轨道Ⅱ上运行的时间。
17.保龄球又称“地滚球”,是一种在木板球道上用球滚击球瓶的室内体育运动。一位保龄球手在练习投掷时,在投球区投出一颗质量的球,如图所示,该球在点以的初速度沿直线运动,并与静止在点的质量的球瓶相撞。球可视为沿直线撞出且速度共线。已知,滚球与轨道间的摩擦力恒为重力的倍,、均可看成质点。取。求:
球在撞上球前瞬间的速度大小;
若撞击后、速度均向右,且大小之比为,碰撞过程中、系统损失的动能;
若换用质量满足的球撞击球瓶,可视为弹性正碰,球瓶获得的速度。
18.如图甲所示为年北京冬奥会上,我国滑雪运动员谷爱凌女子大跳台夺冠瞬间。图乙是女子大跳台完整结构示意图,是助滑坡段,高度;圆弧为起飞段,圆心角,半径,与圆弧相切;为着陆坡段,高度,倾角;为停止区。某次运动员从点由静止开始自由起滑,经过圆弧从与点等高的点飞出,最终恰好沿面从点落入着陆坡段,与圆弧相切于。已知除圆弧轨道外,其余轨道各部分与滑雪板间的动摩擦因数均为,经过圆弧段对点压力为重力的倍,运动员连同滑雪板的质量,各段连接处无能量损失,忽略空气阻力的影响。取,,。求:
运动员在点的速度大小;
运动员经过圆弧段时摩擦力做的功;
运动员在停止区运动的时间为多少?
答案和解析
1.【答案】
【解析】解:、曲线运动的速度沿轨迹上各点的切线方向,所以做曲线运动的物体其速度方向一定变化,则速度一定变化,故A错误;
B、做曲线运动的物体其速度大小可能不变,即动能可能不变,例如匀速圆周运动,故B错误;
C、做曲线运动的物体它所受的合外力可能是恒力,例如平抛运动,故C错误;
D、做曲线运动的物体速度一定变化,则加速度一定不为零,则它所受的合外力一定不为零,故D正确。
故选:。
曲线运动的条件的是合外力与速度不一条直线上,速度方向时刻变化,故曲线运动是变速运动.曲线运动合力一定不能为零。
本题主要考查了曲线运动的条件,解题关键是掌握曲线运动的条件,合外力与速度不一条直线上,知道曲线运动合外力一定不为零,速度方向时刻变化,一定是变速运动。
2.【答案】
【解析】解:、恒力做功的表达式,滑动摩擦力的方向与物体相对运动方向相反,但与运动方向可以相同,也可以相反,物体受滑动摩擦力也有可能位移为零,故可能做负功,也可能做正功,也可以不做功,故A错误;
B、恒力做功的表达式,静摩擦力的方向与物体相对运动趋势方向相反,但与运动方向可以相同,也可以相反,还可以与运动方向垂直,故静摩擦力可以做正功,也可以做负功,也可以不做功,故BC错误,
D、一对相互作用的滑动摩擦力大小相等,方向相反,作用的两个物体位移不同,伴随机械能的损耗转化为内能,所以一对滑动摩擦力做功的总和恒为负值,故D正确;
故选:
功等于力与力的方向上的位移的乘积,这里的位移是相对于参考系的位移;静摩擦力的方向与物体的相对运动趋势方向想法,滑动摩擦力的方向与物体的相对滑动的方向相反.
本题关键要分清相对运动方向与运动方向的关系,前者是相对与与物体接触的另一个物体,而后者是相对与参考系;同时要明确恒力做功的求法.
3.【答案】
【解析】解:,拳击训练时拳头对人的冲量是不变的,根据动量定理可知,带上厚厚的防护垫是增加接触时间,为了减小拳手对自己的冲力,故A错误,B正确;
,练铁砂掌时手对砖头的冲量是不变的,根据动量定理,可知,减少手与砖接触时间从而增加手对砖头的作用力,故CD错误。
故选:。
根据动量定理,动量变化一定时,作用时间越短,作用力就越大,作用时间越长,作用力就越小。
本题考查了对动量定理的理解和应用,要知道动量变化一定时,作用时间与作用力大小成反比。
4.【答案】
【解析】【分析】该题考查汽车恒定功率启动相关知识。分析好物理情景,灵活应用公式是解决本题的关键。
当汽车匀速行驶时,有,由此求解,再根据汽车功率恒定,求解汽车的车速为时的牵引力,最后应用牛顿第二定律求解瞬时加速度的大小。
【解答】
当汽车匀速行驶时,有.
根据,得,
由牛顿第二定律得故B正确,、、D错误
故选B
5.【答案】
【解析】解:,小球从被抛出至落回出发点的过程中,重力的位移为零,则重力做功为零,故A错误;
,小球所受阻力做功为,则合力做功为,故B正确,C错误;
,由能量关系可知,落回出发点时动能为,故D错误。
故选:。
除重力以外的其它力对小球做的功等于小球机械能的变化量,根据功的计算公式分析阻力做的功,由此分析机械能的变化量。
本题主要是考查了功的计算方法和动能定理的应用,明确合外力的总功等于动能的变化。
6.【答案】
【解析】解:、设双星质量分别为、,轨道半径分别为、,角速度相等,均为,根据万有引力定律可知:,距离关系为:,联立解得:,因为,所以的质量一定小于的质量,故A错误;
B、根据线速度与角速度的关系有:、,因为角速度相等,半径,所以的线速度大于的线速度,故B正确;
、周期,由选项可得周期为:,总质量一定,两星间距离越大,周期越大,一定,越大,越小,故CD错误。
故选:。
双星靠相互间的万有引力提供向心力,具有相同的角速度,根据牛顿第二定律列式得到周期表达式进行分析。
此题考查了万有引力定律及其应用,解决本题的关键知道双星靠相互间的万有引力提供向心力,具有相同的角速度。以及会用万有引力提供向心力进行求解。
7.【答案】
【解析】喷出气体的质量为
以喷出气体为研究对象,设气体受到的平均冲力为 ,以向下为正方向,根据动量定理可得
由于在极短时间 内喷出气体,可认为喷出气体的重力冲量忽略不计,故有
解得
根据牛顿第三定律可知返回舱受到的平均反冲力大小为 ,A正确,BCD错误。
故选A。
8.【答案】
【解析】解:、根据图像斜率的物理意义,可知内图像的斜率不变,则小物块加速度不变,故A错误;
,因图像的“面积”等于位移,结合题意,,,可知小物块在内位移是内的位移的倍,故B错误;
,根据求功公式,可知,摩擦力对物块做的功为:,故C正确;
,结合图象,可得,物块相对传送带的位移为:,则物块与传送带间产生的热量为:,故D错误。
故选:。
根据图像斜率的物理意义判断;根据图象与时间轴所围的面积来分析物块的位移关系;根据求功公式求解内摩擦力对物块做功;结合图象,求得,物块相对传送带的位移,再根据公式求解产生的热量。
本题考查了倾斜传送带问题,解决此题的关键是根据图象要能分析出物块的运动情况,再判断其受力情况,灵活应用图象面积的物理意义。
9.【答案】
【解析】解:,在地表附近万有引力等于重力:
探月航天器在接近月球表面的轨道上飞行,则轨道半径为,根据万有引力提供卫星做圆周运动的向心力,则
解得航天器运行周期:
故A正确;
,根据万有引力提供卫星做圆周运动的向心力,则
解得航天器线速度
故B正确;
,根据万有引力提供卫星做圆周运动的向心力,则
解得航天器加速度
故C错误;
,根据万有引力提供卫星做圆周运动的向心力,则
解得航天器角速度
故D错误。
故选:。
探月航天器绕月球做匀速圆周运动,根据万有引力提供向心力,列出等式,可求线速度、角速度、周期和向心加速度。不考虑月球自转的影响,万有引力等于重力。
解决本题的关键要掌握万有引力定律应用的两条基本思路:万有引力等于向心力和万有引力等于重力,要掌描述圆周运动的各个量之间的关系,并能灵活运用。
10.【答案】
【解析】解:,钢球与弹簧枪除受重力外所受的支持力不做功,所以系统机械能守恒;系统所受合外力为零,所以系统动量守恒,故A错误;
,钢球在枪管内压缩弹簧至最大压缩量过程,钢球速度逐渐减小,弹簧枪速度逐渐增大,最大压缩量时,二者有共同速度,所以钢球动能逐渐减小,故B错误;
,弹簧压缩量最大时,规定向左为正方向,由动量守恒定律得
解得弹簧枪和钢球的共同速度为
故C正确;
,由机械能守恒可得,弹簧压缩量最大时,根据能量守恒定律可知弹性势能为:
故D正确。
故选:。
小球与弹簧接触后,根据机械能守恒定律与能量守恒定律的条件分析;根据能量守恒定律结合动量守恒定律解得。
解决本题的关键会根据小球的受力,运用牛顿第二定律,判断机械能与动量是否守恒。
11.【答案】
【解析】C.两物体和随着圆盘转动时,合力提供向心力,有
的轨道半径比的轨道半径大,所以所需向心力大,绳子拉力相等,所以当圆盘转速加快到两物体刚好还未发生滑动时,所受的最大静摩擦力方向沿绳指向圆心,所受的最大静摩擦力方向沿绳背离圆心,故C正确;
设绳子拉力为,以为研究对象,有
以为研究对象有
联立解得
故A正确,B错误;
D.烧断绳子,对分析,若恰好未发生相对滑动有
解得
故此时烧断绳子一定发生相对滑动,同理可得,也一定发生相对滑动,故D错误。
故选AC。
12.【答案】
【解析】解:,依题意可知,重物竖直方向做加速度随时间均匀减小的加速运动,所以重物合力竖直向上,做非匀变速曲线运动,故A错误;
,在时刻,根据牛顿第二定律,由图乙可得
时刻,重物加速度为,拉线对重物拉力
二者的差值为
联立解得:
故B正确;
,根据图像围成的面积表示速度的改变量,可得时刻,重物在竖直方向上的速度大小为
则时刻,重物的速度大小为
根据动能的公式有
故C错误;
,对重物,根据动量定理可得
解得:
故D正确。
故选:。
由于加速度在变化,所以重物做非匀变速曲线运动,根据牛顿第二定律解得;图像围成的面积表示速度的改变量,结合动量定理解答。
本题考查动量定理,解题关键掌握重物运动状态的分析,结合动量定理与牛顿第二定律解答。
13.【答案】;
;
;
【解析】观察主尺的单位为 ,读出主尺的读数是 ,游标尺上的第五条刻度线与主尺上的刻度线对齐,其读数为 ,结合主尺及游标尺的读数得到被测直径为
首先考查在实验的过程中,需要小球两次沿斜槽滚到末端时的速度都水平且大小相同。实验时应使小球每次都从同一位置由静止开始释放,并不需要斜槽的轨道光滑的条件,也不需要测出斜槽末端的高度,但是必须保证斜槽末端水平,故A正确,BC错误;
D.小球与发生正碰时,为使小球在碰后不反弹,要求小球的质量大于小球的质量,故D错误。
故选A。
设、两球的质量分别为和,且;碰前的速度;因为两个金属小球的碰撞视为弹性碰撞,则由动量守恒定律得
由机械能守恒定律得
解得 ,
可见碰后小球的速度小于小球的速度,也小于碰前的速度;所以小球单独滚下落到水平面上的位置为,、碰后在水平面上的落点位置分别为、。
14.【答案】 钩码质量 滑块质量
【解析】解:实验前接通气源,将滑块置于导轨上不挂钩码,给滑块一定的初速度,若,可认为滑块做匀速运动,说明气垫导轨已经水平;
由于挡光时间很短,滑块经过两个光电门时的速度可认为等于挡光过程的平均速度,则有,,滑块从光电门到光电门过程,根据动能定理可得,联立解得;
要验证滑块与钩码组成的系统机械能是否守恒,需要知道钩码减少的重力势能和钩码、滑块增加的动能,故除了需重新测量滑块通过两光电门的时间、外,还需要测出钩码的质量和滑块的质量;
钩码减少的重力势能为,钩码、滑块增加的动能为,若满足关系式则滑块与钩码组成的系统机械能守恒;
故答案为:;;钩码质量;滑块质量;。
实验前接通气源,将滑块置于导轨上不挂钩码,给滑块一定的初速度,若,可认为滑块做匀速运动,说明气垫导轨已经水平;根据挡光时间很短,滑块经过两个光电门时的速度可认为等于挡光过程的平均速度求解;要验证滑块与钩码组成的系统机械能是否守恒,需要知道钩码减少的重力势能和钩码、滑块增加的动能,故除了需重新测量滑块通过两光电门的时间、外,还需要测出钩码的质量和滑块的质量;钩码减少的重力势能和钩码、滑块增加的动能相等则系统机械能守恒。
本题考查了验证机械能守恒定律的实验,熟练掌握实验原理是解题关键,学生需熟练掌握实验原理、误差分析并能应用机械能守恒定律解题。
15.【答案】解:小球从到重力势能的减少量为
小球从到过程,根据机械能守恒定律可得
解得小球运动到点时的速度大小为
小球从到做平抛运动,竖直方向有
解得
代入数据解得:
小球落地点与的水平距离为
答:小球从到重力势能的减少量为;
小球运动到点时的速度大小为;
小球落地点与的水平距离为。
【解析】根据重力做功可表示重力势能的减少.
根据动能定理可解得
根据平抛运动规律可解得水平距离.
本题考查了圆周运动和平抛运动的综合运用,知道圆周运动向心力的来源和平抛运动在水平方向和竖直方向上的运动规律是解决本题的关键.
16.【答案】解:由万有引力充当向心力:,
解得
月球的密度:,解得。
椭圆轨道的半长轴:,
设椭圆轨道上运行周期为,
由开普勒第三定律有:,
在轨道Ⅱ上运行的时间为,
解得。
【解析】根据万有引力提供向心力,结合卫星的轨道半径和周期求出月球的质量,根据月球的体积求出月球的密度;
根据几何关系求出椭圆轨道的半长轴,结合开普勒第三定律求出在轨道上运行的时间。
本题考查了万有引力定律和开普勒第三定律的综合运用,知道在Ⅱ轨道上运行的时间等于椭圆轨道运动周期的一半,结合开普勒第三定律进行求解。
17.【答案】 ; ;
【解析】保龄球从点到点由动能定理得
解得球在撞上球前瞬间的速度大小
撞击后、速度大小分别为 、 ,由动量守恒定律可得
解得
则碰撞过程中、系统损失的动能为
由动量守恒定律和机械能守恒定律得
,
解得
由于 ,所以
18.【答案】解:运动员在点,由牛顿第二定律可得
则
解得运动员在点的速度大小
从点到点由动能定理得
代入数据解得
点与点的高度差为
从点到点由动能定理得
又
代入数据解得
运动员经过圆弧段时由动能定理得
解得运动员经过圆弧段时摩擦力做的功
从点到点由动能定理得
代入数据解得
在段由牛顿第二定律得
则运动员在停止区运动的时间为
答:运动员在点的速度大小为;
运动员经过圆弧段时摩擦力做的功为;
运动员在停止区运动的时间为。
【解析】运动员做圆周运动,根据向心力计算在点的速度大小;
从点到点由动能定理计算速度大小,在圆弧段时由动能定理计算摩擦力做的功;
从点到点由动能定理计算末速度大小,再计算时间。
本题考查了动能定理与圆周运动和平抛运动的综合运用,熟练掌握平抛运动在水平方向和竖直方向上的运动规律是解决本题的关键。
第1页,共1页
同课章节目录
