新版青岛版九年级下数学课件5.2 反比例函数 第三课时
文档属性
| 名称 | 新版青岛版九年级下数学课件5.2 反比例函数 第三课时 |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-13 16:14:16 | ||
图片预览



文档简介
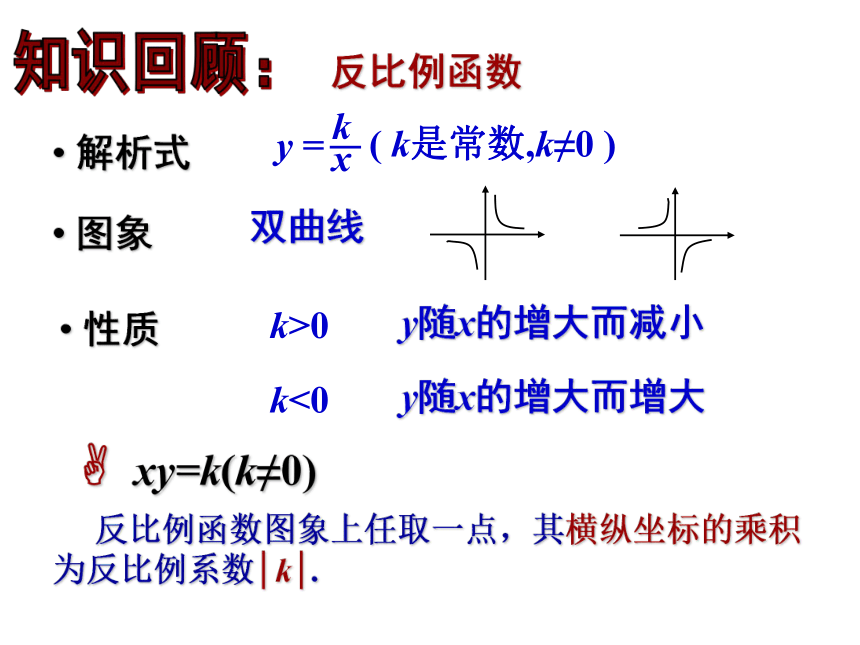
课件16张PPT。5.2反比例函数(3)------反比例函数的综合应用九年级数学下册第五章对函数的再探索反比例函数 解析式 图象 性质双曲线? xy=k(k≠0) 反比例函数图象上任取一点,其横纵坐标的乘积为反比例系数│k│. 知识回顾:1.理解反比例函数中k的几何性质;
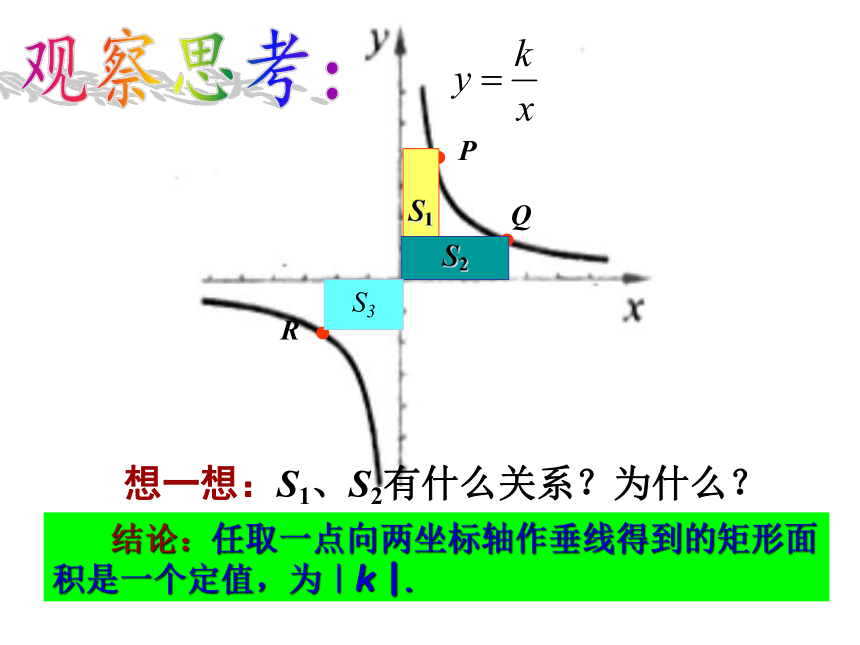
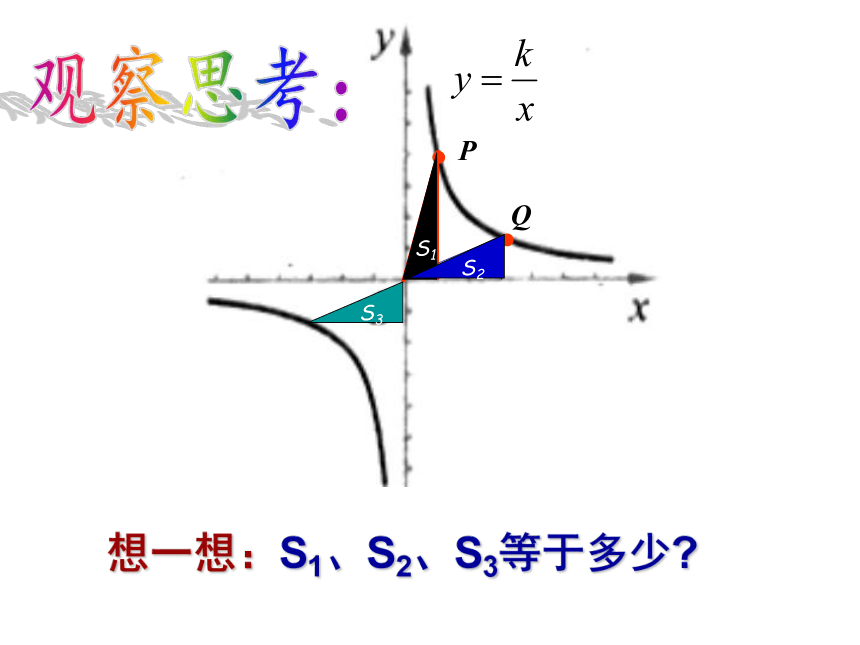
2.能综合运用反比例函数的知识解决相关问题.PQS1S2想一想:S1、S2有什么关系?为什么? 结论:任取一点向两坐标轴作垂线得到的矩形面积是一个定值,为|k |. 观察思考:PQ想一想:S1、S2、S3等于多少?S1S2S3观察思考:1.如图,点P是反比例函数
图象上的一点,若矩形
AOBP的面积是6.请写出
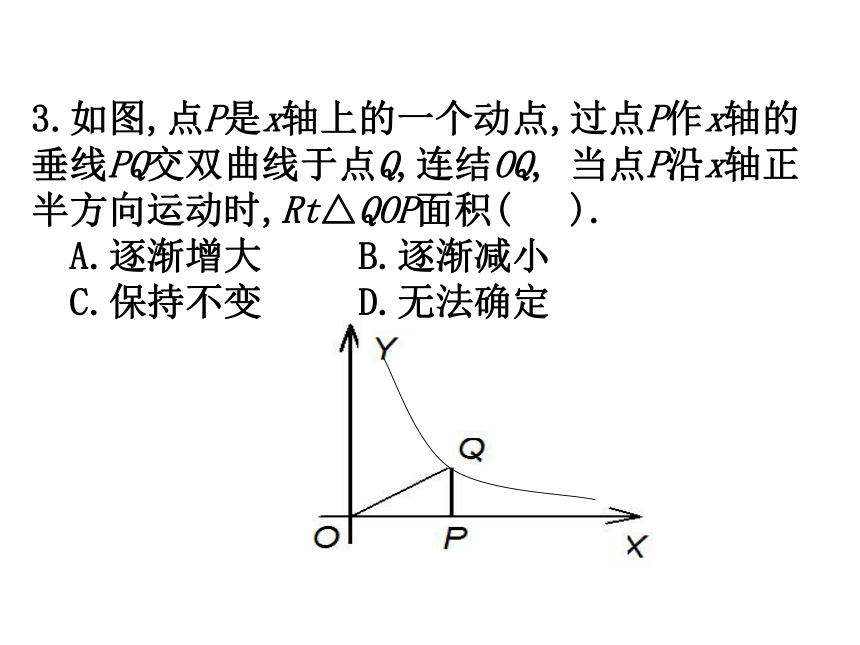
这个反比例函数的解析式.小试牛刀3.如图,点P是x轴上的一个动点,过点P作x轴的垂线PQ交双曲线于点Q,连结OQ, 当点P沿x轴正半方向运动时,Rt△QOP面积( ).
A.逐渐增大 B.逐渐减小
C.保持不变 D.无法确定典型例题:解析:(1)由反比例函数的几何性质可知:
(2)以求得P(5,3),故可知
OA=3,AD=PQ=3,所以:小试牛刀解析:
由点A可求得k=-2x3=-6;
再由 3m=-6可求得m=-2;
所以B(3,-2);
将点A,B代入到y=ax+b即可求得a,b的值。小试牛刀挑战自我:解析:不能相交;假设相交于点A(a,b),
则应有ab=k1=k2,这与k1≠k2相矛盾。
所以不能相交。想一想:反比例函数 上那个点距离原点最近?教材第22页课后练习1、2题.一、反比例函数中k的几何性质
反比例函数图象上任取一点,其横纵坐标的乘积为反比例系数│k│. 二、反比例函数综合运基本思路
首先运用待定系数法求出相关的函数关系式;
再根据要求运用函数性质解决问题. 注意: 任意两个反比例函数的图象均相交.谢谢合作再见!
2.能综合运用反比例函数的知识解决相关问题.PQS1S2想一想:S1、S2有什么关系?为什么? 结论:任取一点向两坐标轴作垂线得到的矩形面积是一个定值,为|k |. 观察思考:PQ想一想:S1、S2、S3等于多少?S1S2S3观察思考:1.如图,点P是反比例函数
图象上的一点,若矩形
AOBP的面积是6.请写出
这个反比例函数的解析式.小试牛刀3.如图,点P是x轴上的一个动点,过点P作x轴的垂线PQ交双曲线于点Q,连结OQ, 当点P沿x轴正半方向运动时,Rt△QOP面积( ).
A.逐渐增大 B.逐渐减小
C.保持不变 D.无法确定典型例题:解析:(1)由反比例函数的几何性质可知:
(2)以求得P(5,3),故可知
OA=3,AD=PQ=3,所以:小试牛刀解析:
由点A可求得k=-2x3=-6;
再由 3m=-6可求得m=-2;
所以B(3,-2);
将点A,B代入到y=ax+b即可求得a,b的值。小试牛刀挑战自我:解析:不能相交;假设相交于点A(a,b),
则应有ab=k1=k2,这与k1≠k2相矛盾。
所以不能相交。想一想:反比例函数 上那个点距离原点最近?教材第22页课后练习1、2题.一、反比例函数中k的几何性质
反比例函数图象上任取一点,其横纵坐标的乘积为反比例系数│k│. 二、反比例函数综合运基本思路
首先运用待定系数法求出相关的函数关系式;
再根据要求运用函数性质解决问题. 注意: 任意两个反比例函数的图象均相交.谢谢合作再见!
