21.2.3. 二次根式的除法 课件(共21张PPT)初中数学华师大版九年级上册
文档属性
| 名称 | 21.2.3. 二次根式的除法 课件(共21张PPT)初中数学华师大版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 281.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-09 21:39:40 | ||
图片预览







文档简介
(共21张PPT)
华东师大版九年级上册
3. 二次根式的除法
学习目标:
1.理解 和 (a > 0,b > 0) ,并运用它们进行计算.
2.利用具体数据,通过学生练习活动,发现规律,归纳出除法规定,并用逆向思维写出逆向等式 及利用它们进行计算和化简.
3.理解最简二次根式的概念,并运用它把不是最 简二次根式的化成最简二次根式.
学习重点:
1.理解 (a > 0,b > 0)及利用它们进行计算和化简.
2.最简二次根式的运用.
学习难点:
发现规律,归纳出二次根式的除法规定.
最简二次根式的运用.
复习导入
二次根式的乘法规定
两个根式相除,怎样进行计算呢?商的算术平方根又等于多少?
及逆向公式
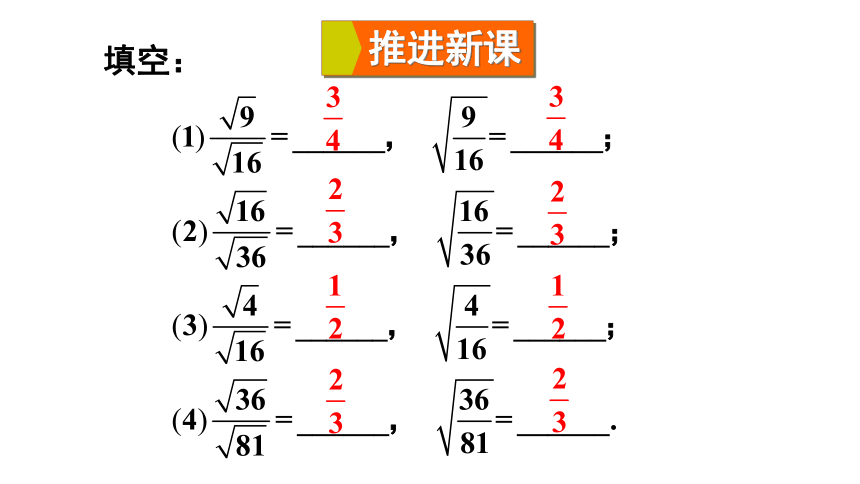
填空:
推进新课
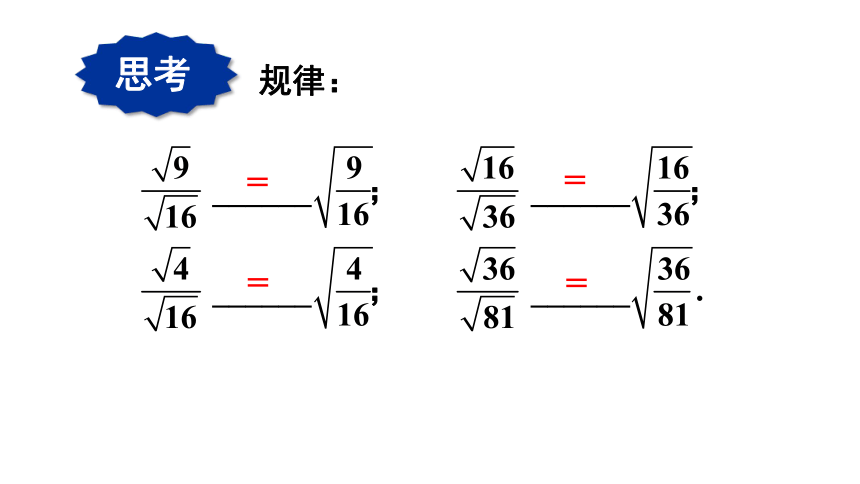
规律:
=
=
=
=
思考
利用计算器计算填空:
=
=
=
=
一般地,有
这就是说,两个算术平方根的商,等于_______________________________.
它们被开方数的商的算术平方根
分母不能为0.
这里为什么要求 a ≥ 0,b > 0?
概括
例3
计算:
解
还可以怎样化简?
上述“概括”中的等式,也可以写成
这就是说,商的算术平方根,等于____
_______________________.
各因式算术平方根的商
利用这个性质可以进行二次根式的化简.
例4
化简 ,使分母中不含二次根式,并且被开方数中不含字母.
解
二次根式的被开方数中含有分母,通常可利用分式的基本性质将分母“配”成完全平方,再“开方”出来。
按照书中例题化简要求,化简后的二次根式有这些特点:
(1)被开方数中不含分母;
(2)被开方数中所有因数(或因式)的幂的指数都小于2.
像这样的二次根式称为最简二次根式.
二次根式的除法,要化去分母中的根号,只要将分子、分母同乘以一个恰当的二次根式就可以了.
如例4,
分母有理化
练习
化简:
练习
寻找分母的有理化因式,应找最简单的有理化因式,也可灵活运用我们学过的性质和法则,简化、优化解答过程.
化简:
1. 化简:
解:
随堂演练
2.已知 ,则 a 的取值范围是___________.
0 < a ≤ 1
0 < a ≤ 1
二次根式的除法
课堂小结
二次根式的化简
反过来,
1.被开方数有分母时,注意分母的取值范围;
2.进行二次根式乘除运算或化简时,
结果要尽可能化简.
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
本课时教学突出学生主体性原则,即通过探究学习,指导学生独立思考,通过具体数据得出规律,再让学生相互交流,或上台展示自己的发现,或表述个人的体验,从中获取成功的体验后,激发学生探究的激情.
华东师大版九年级上册
3. 二次根式的除法
学习目标:
1.理解 和 (a > 0,b > 0) ,并运用它们进行计算.
2.利用具体数据,通过学生练习活动,发现规律,归纳出除法规定,并用逆向思维写出逆向等式 及利用它们进行计算和化简.
3.理解最简二次根式的概念,并运用它把不是最 简二次根式的化成最简二次根式.
学习重点:
1.理解 (a > 0,b > 0)及利用它们进行计算和化简.
2.最简二次根式的运用.
学习难点:
发现规律,归纳出二次根式的除法规定.
最简二次根式的运用.
复习导入
二次根式的乘法规定
两个根式相除,怎样进行计算呢?商的算术平方根又等于多少?
及逆向公式
填空:
推进新课
规律:
=
=
=
=
思考
利用计算器计算填空:
=
=
=
=
一般地,有
这就是说,两个算术平方根的商,等于_______________________________.
它们被开方数的商的算术平方根
分母不能为0.
这里为什么要求 a ≥ 0,b > 0?
概括
例3
计算:
解
还可以怎样化简?
上述“概括”中的等式,也可以写成
这就是说,商的算术平方根,等于____
_______________________.
各因式算术平方根的商
利用这个性质可以进行二次根式的化简.
例4
化简 ,使分母中不含二次根式,并且被开方数中不含字母.
解
二次根式的被开方数中含有分母,通常可利用分式的基本性质将分母“配”成完全平方,再“开方”出来。
按照书中例题化简要求,化简后的二次根式有这些特点:
(1)被开方数中不含分母;
(2)被开方数中所有因数(或因式)的幂的指数都小于2.
像这样的二次根式称为最简二次根式.
二次根式的除法,要化去分母中的根号,只要将分子、分母同乘以一个恰当的二次根式就可以了.
如例4,
分母有理化
练习
化简:
练习
寻找分母的有理化因式,应找最简单的有理化因式,也可灵活运用我们学过的性质和法则,简化、优化解答过程.
化简:
1. 化简:
解:
随堂演练
2.已知 ,则 a 的取值范围是___________.
0 < a ≤ 1
0 < a ≤ 1
二次根式的除法
课堂小结
二次根式的化简
反过来,
1.被开方数有分母时,注意分母的取值范围;
2.进行二次根式乘除运算或化简时,
结果要尽可能化简.
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
本课时教学突出学生主体性原则,即通过探究学习,指导学生独立思考,通过具体数据得出规律,再让学生相互交流,或上台展示自己的发现,或表述个人的体验,从中获取成功的体验后,激发学生探究的激情.
