【多媒体导学案】人教版七年级数学上册第4章第2课时《几何体的三视图与展开图》(教师版,含答案)
文档属性
| 名称 | 【多媒体导学案】人教版七年级数学上册第4章第2课时《几何体的三视图与展开图》(教师版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-13 00:00:00 | ||
图片预览

文档简介
一、学习目标 初步体会从不同方向观察同一物体可能看到不一样的结果;能画出从不同方向看一些常见的立体图形所得到的平面图形;通过观察和动手操作,经历和体验平面图形和立体图形相互转换的过程;重点认识正方体、圆柱、圆锥、棱柱等立体图形及其展开图,培养空间想象力.
二、知识回顾 1.什么是几何图形?几何图形分为哪两类?都包含哪些图形?从实物中抽象出的各种图形统称为几何图形,几何图形分为平面图形和立体图形平面图形包括线段、角、三角形、四边形、平行四边形、矩形、正方形和圆等,立体图形包括长方体、正方体、圆柱、圆锥、棱锥、球等.2.请欣赏漫画并思考,他们为什么会出现争执? ( http: / / www.21cnjy.com )从不同的方向看同一个物体时,可能会看到不同的图形. 3. 欣赏《题西岭壁》,其中“横看成岭侧成峰”一句中,蕴含了怎样的数学道理?题西岭壁——苏轼横看成岭侧成峰,远近高低各不同.不识庐山正面目,只缘身在此山中. ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
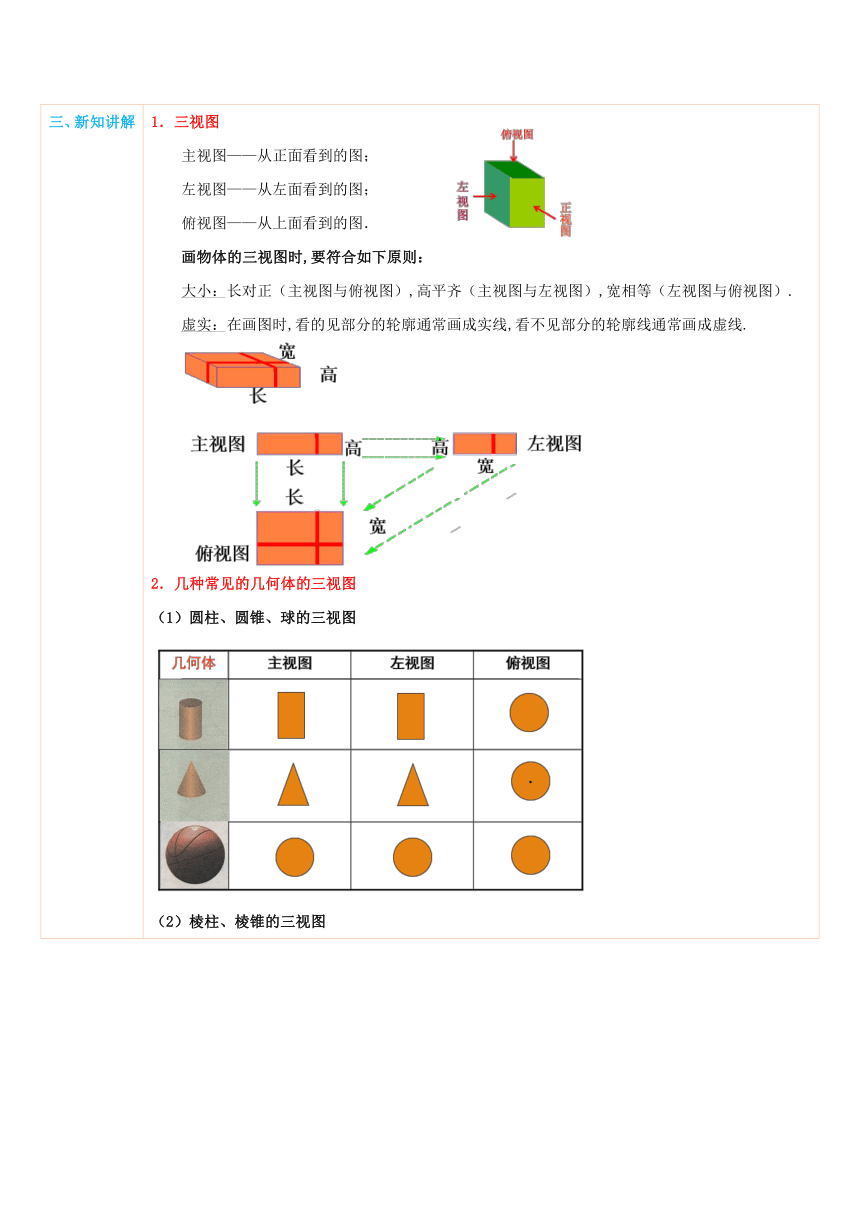
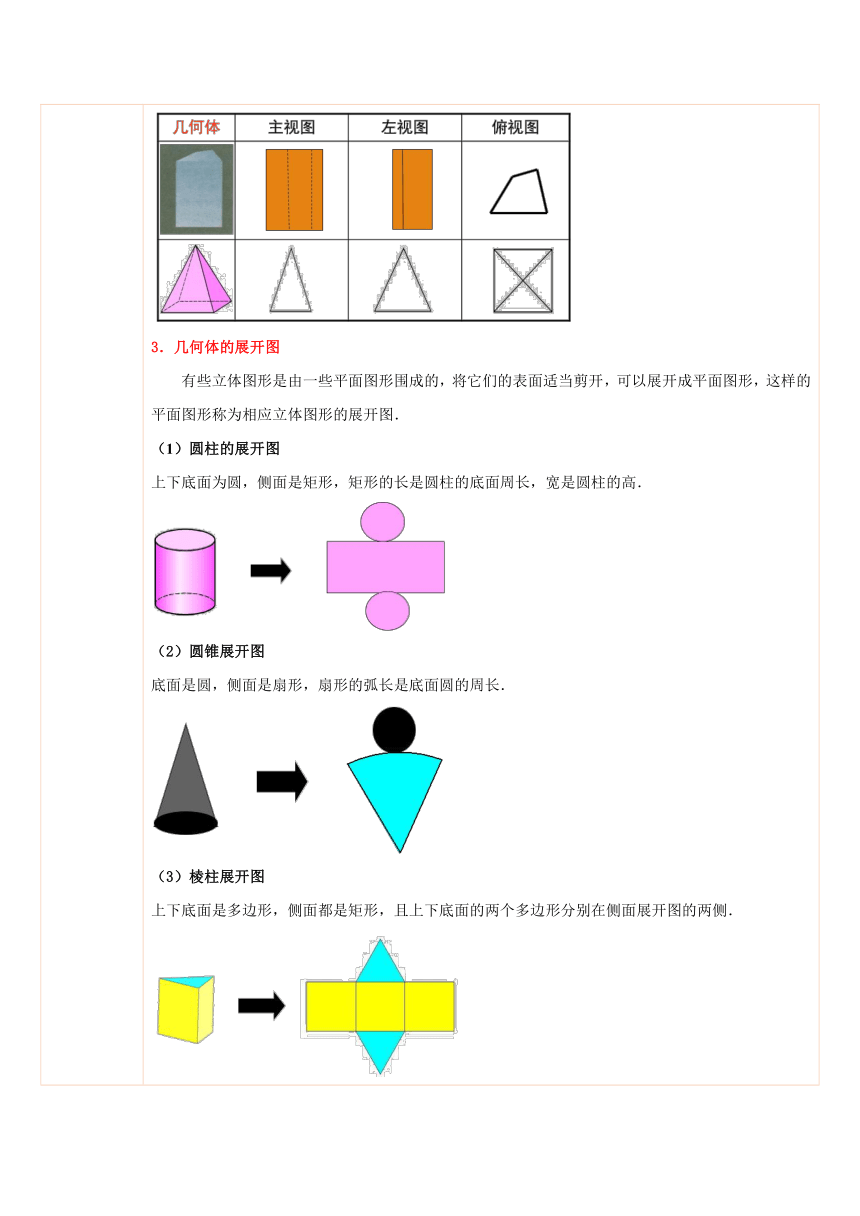
三、新知讲解 1.三视图主视图——从正面看到的图;左视图——从左面看到的图;俯视图——从上面看到的图.画物体的三视图时,要符合如下原则:大小:长对正(主视图与俯视图),高平齐(主视图与左视图),宽相等(左视图与俯视图).虚实:在画图时,看的见部分的轮廓通常画成实线,看不见部分的轮廓线通常画成虚线. ( http: / / www.21cnjy.com )2.几种常见的几何体的三视图(1)圆柱、圆锥、球的三视图 ( http: / / www.21cnjy.com )(2)棱柱、棱锥的三视图 ( http: / / www.21cnjy.com )3.几何体的展开图有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成平面图形,这样的平面图形称为相应立体图形的展开图.(1)圆柱的展开图上下底面为圆,侧面是矩形,矩形的长是圆柱的底面周长,宽是圆柱的高. ( http: / / www.21cnjy.com )(2)圆锥展开图底面是圆,侧面是扇形,扇形的弧长是底面圆的周长. ( http: / / www.21cnjy.com )(3)棱柱展开图上下底面是多边形,侧面都是矩形,且上下底面的两个多边形分别在侧面展开图的两侧. ( http: / / www.21cnjy.com )(4)棱锥展开图底面是多边形,侧面都是三角形,这些三角形的公共顶点就是棱锥的顶点. ( http: / / www.21cnjy.com )(5)正方体展开图将正方体展开后得到的由六个小正方形构成的平面图形就是正方体的展开图.正方体的11种展开图:类别特征图形1-4-1型(6种)中间4个正方形连排,两侧各有1个正方形1-3-2型(3种)中间3个正方形连排,两侧分别有1个,2个正方形2-2-2型(1种)2个正方形连排,成阶梯状3-3型(1)两行只能有1个正方形相连
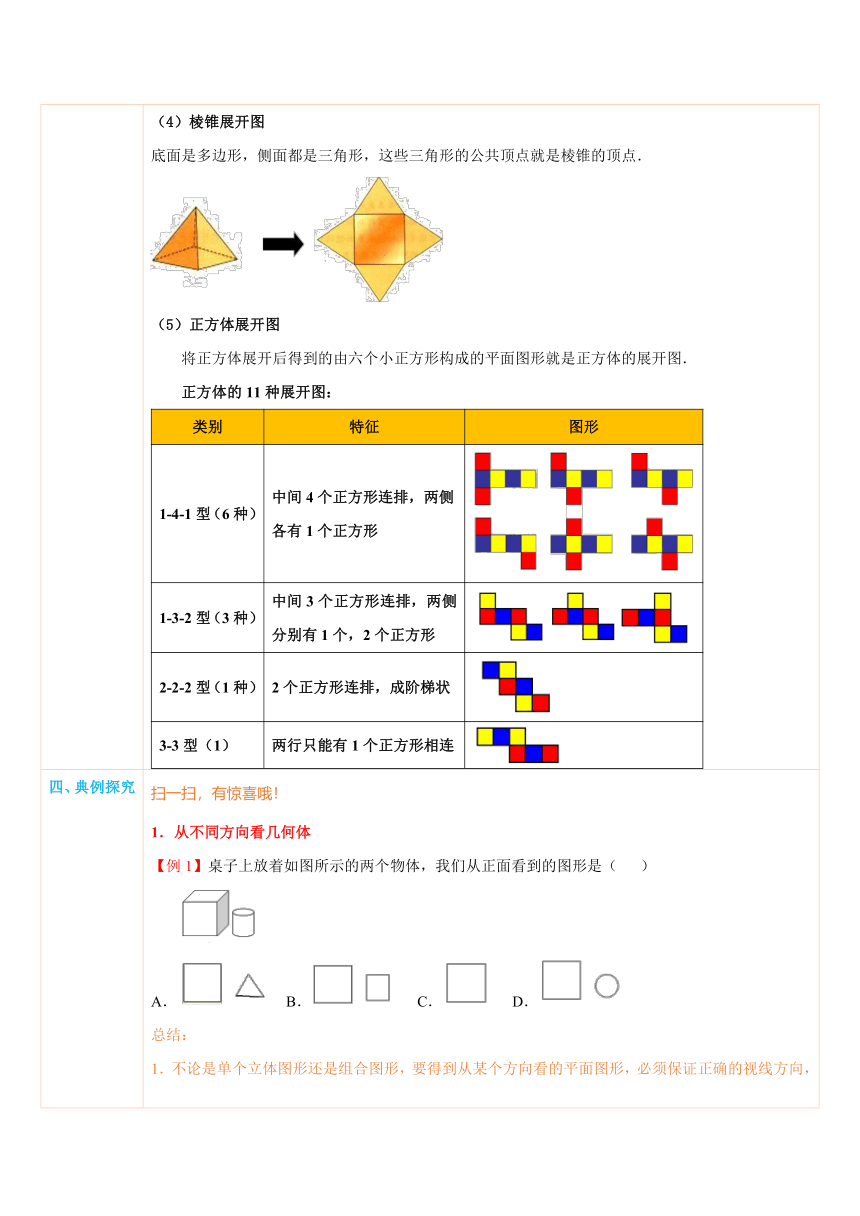
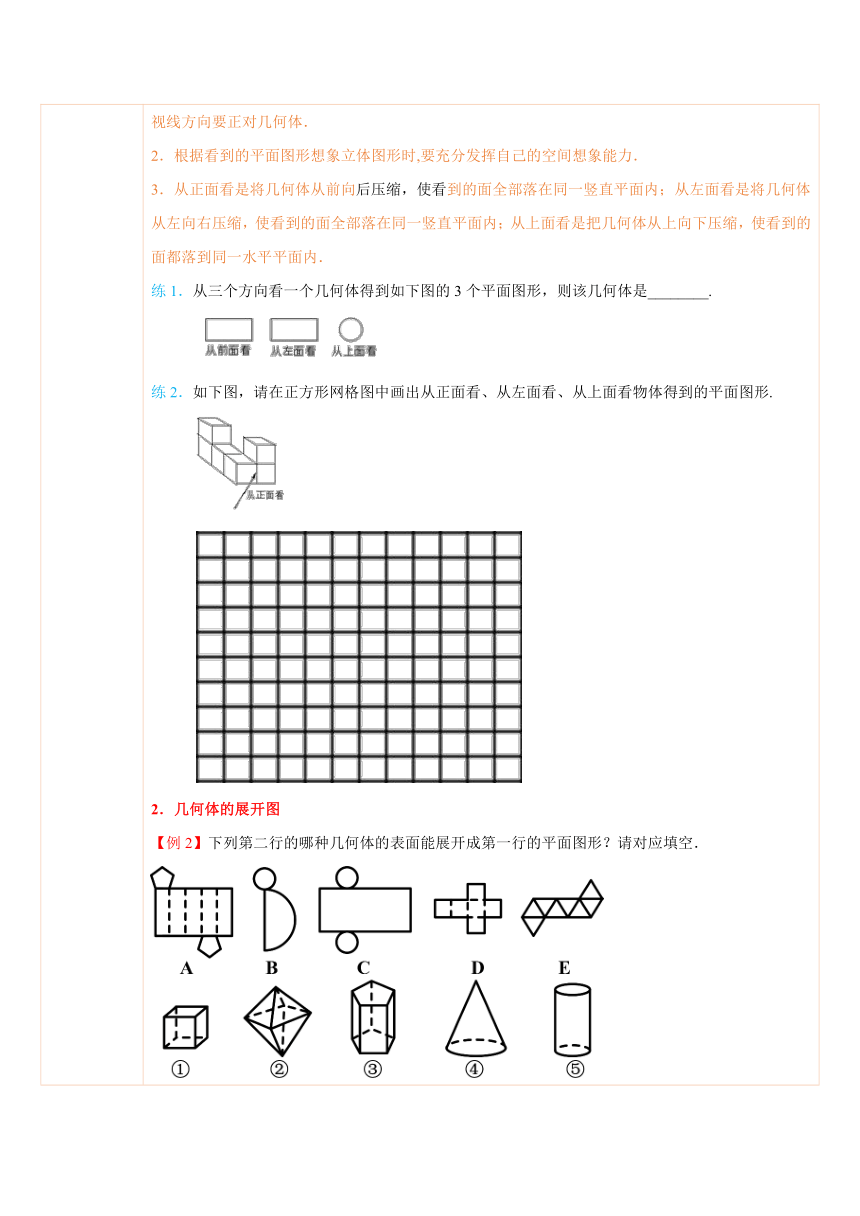
四、典例探究 扫一扫,有惊喜哦!1.从不同方向看几何体【例1】桌子上放着如图所示的两个物体,我们从正面看到的图形是( )A. B. C. D.总结:1.不论是单个立体图形还是组合图形,要得到从某个方向看的平面图形,必须保证正确的视线方向,视线方向要正对几何体.2.根据看到的平面图形想象立体图形时,要充分发挥自己的空间想象能力.3.从正面看是将几何体从前向后压缩,使看 ( http: / / www.21cnjy.com )到的面全部落在同一竖直平面内;从左面看是将几何体从左向右压缩,使看到的面全部落在同一竖直平面内;从上面看是把几何体从上向下压缩,使看到的面都落到同一水平平面内.练1.从三个方向看一个几何体得到如下图的3个平面图形,则该几何体是________.练2.如下图,请在正方形网格图中画出从正面看、从左面看、从上面看物体得到的平面图形. ( http: / / www.21cnjy.com )2.几何体的展开图【例2】下列第二行的哪种几何体的表面能展开成第一行的平面图形?请对应填空. ( http: / / www.21cnjy.com )①: ;②: ;③: ;④: ;⑤: .总结:1.沿多面体的棱可以将多面体剪开成平面图形,若干个平面图形也可以围成一个多面体.2.同一个多面体沿不同的棱剪开,得到的平面展开图是不一样的,也就是说,同一个立体图形可以有多种不同的展开图.3.不是所有立体图形都有平面展开图,比如球体就没有平面展开图.练3.(2014 鼓楼区二模)图①是由白色 ( http: / / www.21cnjy.com )纸板拼成的立体图形,将它的两个面的外表面涂上颜色,如图②,则下列图形中,是图②的表面展开图的是( ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) B. C. D.练4.下列展开图对应的立体图形是_________________. ( http: / / www.21cnjy.com )3.正方体展开图的识别【例3】下列图形中可以作为一个正方体的展开图的是( ) ( http: / / www.21cnjy.com ) B. C. D.总结:正方体展开图一共有11种,4句口诀就能帮助记忆.口诀1:中间4个一连串,两边各一随便放.(有6种,如下图) ( http: / / www.21cnjy.com ) 口诀2:二三紧连错一个,三一相连一随便.(有3种,如下图) ( http: / / www.21cnjy.com )口诀3:两两相连各错一.(有1种,如下图)口诀4:三个两排一对齐. (有1种,如下图)注意:正方体展开图中不会出现“7”“田”“凹”字形状.练5.(2014秋 滕州市月考)图中是正方体的展开图的个数是( ) ( http: / / www.21cnjy.com )A.5个 B.3个 C.4个 D.6个识别带标志的正方体的展开图【例4】(2014秋 博野县期末)如左图所示的正方体沿某些棱展开后,能得到的图形是( ) ( http: / / www.21cnjy.com )A. ( http: / / www.21cnjy.com )B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com )D. ( http: / / www.21cnjy.com )总结:识别带标志的正方体的展开图时,要注意观察以下几点:观察正方体中带标志的几个面是相邻还是相对;观察正方体中带标志的几个面相邻(或相对)的位置关系.练6. 如图,有一个正方体纸盒,在它的三个侧面分别画有三角形、正方形和圆,现用一把简答沿着它的棱剪开成一个平面图形,则展开图可以是( ) ( http: / / www.21cnjy.com ) B. C. D.正方体展开图找对面【例5】(2015 平定县一模)2015年 ( http: / / www.21cnjy.com ),县委、县政府做出了“小微企业富民,大中企业强县,唱响千年文化,建设美好平定”的决策,如图是小明制作的一个正方体的表面展开图,原正方体中与“建”字所在的面相对的面上标的字是( ) ( http: / / www.21cnjy.com )A.美 B.好 C.平 D.定总结:在正方体展开图中找相 ( http: / / www.21cnjy.com )对面,需要较强的空间想象能力,需要在头脑中让小正方形“动”起来.除了通过想像、动手折纸以及模型模拟之外,还有两个“绝招”来找对面.绝招1:隔空相对.展开图中,凡是有3个小正方形排成一排的,中间隔一个小正方形的两个正方形相对.如图, ,B和D相对,C和E相对,剩下的A和F自然相对.绝招2:邻四对一.在一个正方体中,每个面都有四个面与之相邻,另一个面则相对,在正方体展开图中,各面的相邻关系是不会改变的.如图, ,D与C、E、F相邻,与B有一个公共顶点,也相邻,则剩下的A必然与D相对.练7.(2014秋 南岸区校级期中)根据如图中骨骰子的三种不同状态显示的数字,请你推出“?”处的数字应为 . ( http: / / www.21cnjy.com )
五、课后小测 一、选择题1.(2014 谷城县模拟)下列图形的主视图与其它三个不同的是( )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )2.(2014秋 温州期末)下图是某长方体的展开图,其中错误的是( )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )3.(2014 宁德)下列图形中,不是正方体表面展开图的是( )A. B. C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )4.(2013 房山区二模)在正方体的表面上画有如图所示的粗线,则其展开后正确的是( ) ( http: / / www.21cnjy.com )A.B.C.D.5.(2014 贵阳)一个正方体的表面 ( http: / / www.21cnjy.com )展开图如图所示,六个面上各有一字,连起来的意思是“预祝中考成功”,把它折成正方体后,与“成”相对的字是( ) ( http: / / www.21cnjy.com )A.中 B.功 C.考 D.祝二、填空题6.(2013秋 徐州期末)如图所示的四幅平面图中,是三棱柱的表面展开图的有 .(只填序号) ( http: / / www.21cnjy.com )7.(2010秋 下城区期末)右面是两个立体图形的三视图,请填出它们的名称是: 和 . ( http: / / www.21cnjy.com )8.(2013 庐阳区校级模拟)如图,添加一个相同的正方形后,能构成一个正方体的平面展开图.则不同的添加方式共有 种. ( http: / / www.21cnjy.com )9.(2012秋 磐石市校级期末) ( http: / / www.21cnjy.com )如图所示,在图中再添上一个面后,折叠后才能围成一个正方体.下面是四位同学补画的情况,其中正确的是 (填序号). ( http: / / www.21cnjy.com )三、解答题10.画出图中无盖正方体纸盒的一种表面展开图. ( http: / / www.21cnjy.com )11.如图,下列图形能折叠成什么图形? ( http: / / www.21cnjy.com ) (2) (3) (4) .
例题详解:
【例1】解析:从正面看这两个物体,可以看到正方体的前面即一个正方形,还有圆柱的侧面即一个长方形,所以选B.
【例2】分析:根据几何体的平面展开 ( http: / / www.21cnjy.com )图的特征可知:A是五棱柱的展开图;B是圆锥的展开图;C是圆柱的展开图;D是正方体的展开图;E是两个四棱锥的展开图.
解答:解:根据几何体的平面展开图的特征可知:
①:D;②:E;③:A;④:B;⑤:C.
故答案为:D,E,A,B,C.
点评:此题考查了几何体的展开图,熟记常见几何体的平面展开图的特征是解决此类问题的关键.
【例3】分析:正方体的展开图有11种,其中1 ( http: / / www.21cnjy.com )-4-1型共有6种,2-3-1型有3种,3-3型有1种,2-2-2型有1种.正方体中不能有“7”“田”“凹”字形.
解答:选项A中有“田”字, ( http: / / www.21cnjy.com )所以不是正方体的展开图;选项B呈“7”字形,所以不是正方体的展开图;选项D中有“凹”字,所以不是正方体的展开图.只有选项C是正方体的展开图,故选C.
点评:此题考查了正方体的展开图,熟记11种正方体展开图是解题关键.
【例4】分析:由平面图形的折叠及立体图形的表面展开图的特点解题.
解答:解:由原正方体知,带图案的三个面相交于一点,而通过折叠后A、C都不符合,且D折叠后图案的位置正好相反,所以能得到的图形是B.故选B.
点评:解决此类问题,要充分考虑带有各种符号的面的特点及位置.
【例5】分析:正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
解答:解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“设”与“好”是相对面,
“建”与“定”是相对面,
“美”与“平”是相对面.
故选D.
点评:本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
练习答案:
练1.解析:从三个方向看可得到两个长方形和一个圆,只有观察竖直放置的圆柱能得到这几个皮昂面图形,故填圆柱.
练2.解析:从正面看,能够看到4个正方体侧面,组成2行2列的4个正方形组成的平面图形;
从左面看,能够看到5个正方体侧面,得到3列2行的5个正方形组成的平面图形;
从上面看,可以看到4个正方体侧面,得到的平面图共有2列,左边一列有3个正方形,右边一列只有1个正方形.如图.
练3.分析:由平面图形的折叠及立体图形的表面展开图的特点解题.
解答:解:由图中阴影部分的位置,首先可以排除C、D,
又阴影部分正方形在左,三角形在右,而且相邻,故只有选项B符合题意.
故选:B.
点评:此题主要考查了几何 ( http: / / www.21cnjy.com )体的展开图,本题虽然是选择题,但答案的获得需要学生经历一定的实验操作过程,当然学生也可以将操作活动转化为思维活动,在头脑中模拟(想象)折纸、翻转活动,较好地考查了学生空间观念.
练4.分析:根据圆锥、正五棱柱,圆锥以及正四棱锥的展开图填空.
解答:解:圆锥的平面展开图是扇形和圆,所以该图是圆锥的展开图;
正五棱柱的平面展开图是矩形和正五边形,所以该图是正五棱柱的展开图;
圆柱的平面展开图是圆和矩形,所以该图是圆柱的展开图;
正四棱锥的平面展开图是由等腰三角形和正方形组成,所以该图是正四棱锥的展开图.
故答案是:圆锥,正五棱柱,圆柱,正四棱锥.
点评:本题考查了立体图形的展开图:立体图形的展开图体现了平面图形与立体图形的联系.立体图形问题可以转化为平面图形问题解决.
练5.分析:正方体的展开图有11中情况:1﹣4﹣1型共6种,1﹣3﹣2型共3种,2﹣2﹣2型一种,3﹣3型一种,由此判定找出答案即可.
解答:解:属于1﹣4﹣1型有(1)(2)(6);
属于1﹣3﹣2型有(3);
(4)也可以.
(5)(7)(8)都不属于正方体的展开图.
故选:D.
点评:此题考查正方体的展开图,注意识记基本类型,更快解决实际问题.
练6. 分析:由平面图形的折叠及正方体展开图的特点解题.
解答:由原正方体知,带图案的三个面相较 ( http: / / www.21cnjy.com )于一点,属于相邻,所以可以排除选项A和B;还可以从原正方体中看出正方形图案下面是圆形图案,右侧是三角形图案,选项D正好相反.故选C.
点评:解决此类问题,要充分考虑带有各种符号的面的特点及位置.
练7.分析:要通过观察骰子上的点数,用逐一排除法,便可找出答案.
解答:解:根据A可知,1和4,5相邻,
根据B可知,1和2,3相邻,
所以“?”处的数是6.
故答案为:6.
点评:主要考查了正方体相对两个面上的文 ( http: / / www.21cnjy.com )字.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.
课后小测答案:
1.解:A、主视图为长方形;
B、主视图为长方形;
C、主视图为三角形;
D、主视图为长方形.
则主视图与其他三个不相同的是C.
故选C.
2.解:由四棱柱四个侧面和上下两个底面的特征可知,A,B,D选项可以拼成一个长方体,而C选项,上底面不可能有两个,故不是长方体的展开图.
故选C.
3.解:A围成几何体时,有两个面重合,故不能围成正方体;
B、C、D均能围成正方体.
故选A.
4.解:由带有各种符号的面的特点及位置,可知只有选项D符合.
故选D.
5.解:这是一个正方体的平面展开图,共有六个面,其中“成”与面“功”相对,“预”与“祝”相对,“中”与“考”相对.
故选:B.
6.解:三棱柱的两底展开是三角形,侧面展开是三个矩形,
故答案为:①②③.
7.解:∵正视图和左视图是三角形,
∴几何体是椎体,
∵俯视图的大致轮廓是三角形,
∴该几何体是三棱锥;
∵正视图和左视图的大致轮廓是长方形,
∴该几何体是柱体,
∵俯视图是六边形,
∴该几何体是六棱柱.
8.解:能构成这个正方体的表面展开图的有:
( http: / / www.21cnjy.com )
共4种情况.
故答案为:4.
9.解:图形(1)是“田”字格,不能折成正方体;
图形(2)可折成正方体.
图形(3)是“凹”字格,不能折成正方体;
图形(4)有两个面重叠,不能折成正方体.
故答案为:(2).
10.解:如图所示:(答案不唯一)
( http: / / www.21cnjy.com )
12.解:(1)圆柱,(2)五棱柱,(3)圆锥,(4)三棱柱,
故答案为:圆柱,五棱柱,圆锥,三棱柱.
二、知识回顾 1.什么是几何图形?几何图形分为哪两类?都包含哪些图形?从实物中抽象出的各种图形统称为几何图形,几何图形分为平面图形和立体图形平面图形包括线段、角、三角形、四边形、平行四边形、矩形、正方形和圆等,立体图形包括长方体、正方体、圆柱、圆锥、棱锥、球等.2.请欣赏漫画并思考,他们为什么会出现争执? ( http: / / www.21cnjy.com )从不同的方向看同一个物体时,可能会看到不同的图形. 3. 欣赏《题西岭壁》,其中“横看成岭侧成峰”一句中,蕴含了怎样的数学道理?题西岭壁——苏轼横看成岭侧成峰,远近高低各不同.不识庐山正面目,只缘身在此山中. ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
三、新知讲解 1.三视图主视图——从正面看到的图;左视图——从左面看到的图;俯视图——从上面看到的图.画物体的三视图时,要符合如下原则:大小:长对正(主视图与俯视图),高平齐(主视图与左视图),宽相等(左视图与俯视图).虚实:在画图时,看的见部分的轮廓通常画成实线,看不见部分的轮廓线通常画成虚线. ( http: / / www.21cnjy.com )2.几种常见的几何体的三视图(1)圆柱、圆锥、球的三视图 ( http: / / www.21cnjy.com )(2)棱柱、棱锥的三视图 ( http: / / www.21cnjy.com )3.几何体的展开图有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成平面图形,这样的平面图形称为相应立体图形的展开图.(1)圆柱的展开图上下底面为圆,侧面是矩形,矩形的长是圆柱的底面周长,宽是圆柱的高. ( http: / / www.21cnjy.com )(2)圆锥展开图底面是圆,侧面是扇形,扇形的弧长是底面圆的周长. ( http: / / www.21cnjy.com )(3)棱柱展开图上下底面是多边形,侧面都是矩形,且上下底面的两个多边形分别在侧面展开图的两侧. ( http: / / www.21cnjy.com )(4)棱锥展开图底面是多边形,侧面都是三角形,这些三角形的公共顶点就是棱锥的顶点. ( http: / / www.21cnjy.com )(5)正方体展开图将正方体展开后得到的由六个小正方形构成的平面图形就是正方体的展开图.正方体的11种展开图:类别特征图形1-4-1型(6种)中间4个正方形连排,两侧各有1个正方形1-3-2型(3种)中间3个正方形连排,两侧分别有1个,2个正方形2-2-2型(1种)2个正方形连排,成阶梯状3-3型(1)两行只能有1个正方形相连
四、典例探究 扫一扫,有惊喜哦!1.从不同方向看几何体【例1】桌子上放着如图所示的两个物体,我们从正面看到的图形是( )A. B. C. D.总结:1.不论是单个立体图形还是组合图形,要得到从某个方向看的平面图形,必须保证正确的视线方向,视线方向要正对几何体.2.根据看到的平面图形想象立体图形时,要充分发挥自己的空间想象能力.3.从正面看是将几何体从前向后压缩,使看 ( http: / / www.21cnjy.com )到的面全部落在同一竖直平面内;从左面看是将几何体从左向右压缩,使看到的面全部落在同一竖直平面内;从上面看是把几何体从上向下压缩,使看到的面都落到同一水平平面内.练1.从三个方向看一个几何体得到如下图的3个平面图形,则该几何体是________.练2.如下图,请在正方形网格图中画出从正面看、从左面看、从上面看物体得到的平面图形. ( http: / / www.21cnjy.com )2.几何体的展开图【例2】下列第二行的哪种几何体的表面能展开成第一行的平面图形?请对应填空. ( http: / / www.21cnjy.com )①: ;②: ;③: ;④: ;⑤: .总结:1.沿多面体的棱可以将多面体剪开成平面图形,若干个平面图形也可以围成一个多面体.2.同一个多面体沿不同的棱剪开,得到的平面展开图是不一样的,也就是说,同一个立体图形可以有多种不同的展开图.3.不是所有立体图形都有平面展开图,比如球体就没有平面展开图.练3.(2014 鼓楼区二模)图①是由白色 ( http: / / www.21cnjy.com )纸板拼成的立体图形,将它的两个面的外表面涂上颜色,如图②,则下列图形中,是图②的表面展开图的是( ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) B. C. D.练4.下列展开图对应的立体图形是_________________. ( http: / / www.21cnjy.com )3.正方体展开图的识别【例3】下列图形中可以作为一个正方体的展开图的是( ) ( http: / / www.21cnjy.com ) B. C. D.总结:正方体展开图一共有11种,4句口诀就能帮助记忆.口诀1:中间4个一连串,两边各一随便放.(有6种,如下图) ( http: / / www.21cnjy.com ) 口诀2:二三紧连错一个,三一相连一随便.(有3种,如下图) ( http: / / www.21cnjy.com )口诀3:两两相连各错一.(有1种,如下图)口诀4:三个两排一对齐. (有1种,如下图)注意:正方体展开图中不会出现“7”“田”“凹”字形状.练5.(2014秋 滕州市月考)图中是正方体的展开图的个数是( ) ( http: / / www.21cnjy.com )A.5个 B.3个 C.4个 D.6个识别带标志的正方体的展开图【例4】(2014秋 博野县期末)如左图所示的正方体沿某些棱展开后,能得到的图形是( ) ( http: / / www.21cnjy.com )A. ( http: / / www.21cnjy.com )B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com )D. ( http: / / www.21cnjy.com )总结:识别带标志的正方体的展开图时,要注意观察以下几点:观察正方体中带标志的几个面是相邻还是相对;观察正方体中带标志的几个面相邻(或相对)的位置关系.练6. 如图,有一个正方体纸盒,在它的三个侧面分别画有三角形、正方形和圆,现用一把简答沿着它的棱剪开成一个平面图形,则展开图可以是( ) ( http: / / www.21cnjy.com ) B. C. D.正方体展开图找对面【例5】(2015 平定县一模)2015年 ( http: / / www.21cnjy.com ),县委、县政府做出了“小微企业富民,大中企业强县,唱响千年文化,建设美好平定”的决策,如图是小明制作的一个正方体的表面展开图,原正方体中与“建”字所在的面相对的面上标的字是( ) ( http: / / www.21cnjy.com )A.美 B.好 C.平 D.定总结:在正方体展开图中找相 ( http: / / www.21cnjy.com )对面,需要较强的空间想象能力,需要在头脑中让小正方形“动”起来.除了通过想像、动手折纸以及模型模拟之外,还有两个“绝招”来找对面.绝招1:隔空相对.展开图中,凡是有3个小正方形排成一排的,中间隔一个小正方形的两个正方形相对.如图, ,B和D相对,C和E相对,剩下的A和F自然相对.绝招2:邻四对一.在一个正方体中,每个面都有四个面与之相邻,另一个面则相对,在正方体展开图中,各面的相邻关系是不会改变的.如图, ,D与C、E、F相邻,与B有一个公共顶点,也相邻,则剩下的A必然与D相对.练7.(2014秋 南岸区校级期中)根据如图中骨骰子的三种不同状态显示的数字,请你推出“?”处的数字应为 . ( http: / / www.21cnjy.com )
五、课后小测 一、选择题1.(2014 谷城县模拟)下列图形的主视图与其它三个不同的是( )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )2.(2014秋 温州期末)下图是某长方体的展开图,其中错误的是( )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )3.(2014 宁德)下列图形中,不是正方体表面展开图的是( )A. B. C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )4.(2013 房山区二模)在正方体的表面上画有如图所示的粗线,则其展开后正确的是( ) ( http: / / www.21cnjy.com )A.B.C.D.5.(2014 贵阳)一个正方体的表面 ( http: / / www.21cnjy.com )展开图如图所示,六个面上各有一字,连起来的意思是“预祝中考成功”,把它折成正方体后,与“成”相对的字是( ) ( http: / / www.21cnjy.com )A.中 B.功 C.考 D.祝二、填空题6.(2013秋 徐州期末)如图所示的四幅平面图中,是三棱柱的表面展开图的有 .(只填序号) ( http: / / www.21cnjy.com )7.(2010秋 下城区期末)右面是两个立体图形的三视图,请填出它们的名称是: 和 . ( http: / / www.21cnjy.com )8.(2013 庐阳区校级模拟)如图,添加一个相同的正方形后,能构成一个正方体的平面展开图.则不同的添加方式共有 种. ( http: / / www.21cnjy.com )9.(2012秋 磐石市校级期末) ( http: / / www.21cnjy.com )如图所示,在图中再添上一个面后,折叠后才能围成一个正方体.下面是四位同学补画的情况,其中正确的是 (填序号). ( http: / / www.21cnjy.com )三、解答题10.画出图中无盖正方体纸盒的一种表面展开图. ( http: / / www.21cnjy.com )11.如图,下列图形能折叠成什么图形? ( http: / / www.21cnjy.com ) (2) (3) (4) .
例题详解:
【例1】解析:从正面看这两个物体,可以看到正方体的前面即一个正方形,还有圆柱的侧面即一个长方形,所以选B.
【例2】分析:根据几何体的平面展开 ( http: / / www.21cnjy.com )图的特征可知:A是五棱柱的展开图;B是圆锥的展开图;C是圆柱的展开图;D是正方体的展开图;E是两个四棱锥的展开图.
解答:解:根据几何体的平面展开图的特征可知:
①:D;②:E;③:A;④:B;⑤:C.
故答案为:D,E,A,B,C.
点评:此题考查了几何体的展开图,熟记常见几何体的平面展开图的特征是解决此类问题的关键.
【例3】分析:正方体的展开图有11种,其中1 ( http: / / www.21cnjy.com )-4-1型共有6种,2-3-1型有3种,3-3型有1种,2-2-2型有1种.正方体中不能有“7”“田”“凹”字形.
解答:选项A中有“田”字, ( http: / / www.21cnjy.com )所以不是正方体的展开图;选项B呈“7”字形,所以不是正方体的展开图;选项D中有“凹”字,所以不是正方体的展开图.只有选项C是正方体的展开图,故选C.
点评:此题考查了正方体的展开图,熟记11种正方体展开图是解题关键.
【例4】分析:由平面图形的折叠及立体图形的表面展开图的特点解题.
解答:解:由原正方体知,带图案的三个面相交于一点,而通过折叠后A、C都不符合,且D折叠后图案的位置正好相反,所以能得到的图形是B.故选B.
点评:解决此类问题,要充分考虑带有各种符号的面的特点及位置.
【例5】分析:正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
解答:解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“设”与“好”是相对面,
“建”与“定”是相对面,
“美”与“平”是相对面.
故选D.
点评:本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
练习答案:
练1.解析:从三个方向看可得到两个长方形和一个圆,只有观察竖直放置的圆柱能得到这几个皮昂面图形,故填圆柱.
练2.解析:从正面看,能够看到4个正方体侧面,组成2行2列的4个正方形组成的平面图形;
从左面看,能够看到5个正方体侧面,得到3列2行的5个正方形组成的平面图形;
从上面看,可以看到4个正方体侧面,得到的平面图共有2列,左边一列有3个正方形,右边一列只有1个正方形.如图.
练3.分析:由平面图形的折叠及立体图形的表面展开图的特点解题.
解答:解:由图中阴影部分的位置,首先可以排除C、D,
又阴影部分正方形在左,三角形在右,而且相邻,故只有选项B符合题意.
故选:B.
点评:此题主要考查了几何 ( http: / / www.21cnjy.com )体的展开图,本题虽然是选择题,但答案的获得需要学生经历一定的实验操作过程,当然学生也可以将操作活动转化为思维活动,在头脑中模拟(想象)折纸、翻转活动,较好地考查了学生空间观念.
练4.分析:根据圆锥、正五棱柱,圆锥以及正四棱锥的展开图填空.
解答:解:圆锥的平面展开图是扇形和圆,所以该图是圆锥的展开图;
正五棱柱的平面展开图是矩形和正五边形,所以该图是正五棱柱的展开图;
圆柱的平面展开图是圆和矩形,所以该图是圆柱的展开图;
正四棱锥的平面展开图是由等腰三角形和正方形组成,所以该图是正四棱锥的展开图.
故答案是:圆锥,正五棱柱,圆柱,正四棱锥.
点评:本题考查了立体图形的展开图:立体图形的展开图体现了平面图形与立体图形的联系.立体图形问题可以转化为平面图形问题解决.
练5.分析:正方体的展开图有11中情况:1﹣4﹣1型共6种,1﹣3﹣2型共3种,2﹣2﹣2型一种,3﹣3型一种,由此判定找出答案即可.
解答:解:属于1﹣4﹣1型有(1)(2)(6);
属于1﹣3﹣2型有(3);
(4)也可以.
(5)(7)(8)都不属于正方体的展开图.
故选:D.
点评:此题考查正方体的展开图,注意识记基本类型,更快解决实际问题.
练6. 分析:由平面图形的折叠及正方体展开图的特点解题.
解答:由原正方体知,带图案的三个面相较 ( http: / / www.21cnjy.com )于一点,属于相邻,所以可以排除选项A和B;还可以从原正方体中看出正方形图案下面是圆形图案,右侧是三角形图案,选项D正好相反.故选C.
点评:解决此类问题,要充分考虑带有各种符号的面的特点及位置.
练7.分析:要通过观察骰子上的点数,用逐一排除法,便可找出答案.
解答:解:根据A可知,1和4,5相邻,
根据B可知,1和2,3相邻,
所以“?”处的数是6.
故答案为:6.
点评:主要考查了正方体相对两个面上的文 ( http: / / www.21cnjy.com )字.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.
课后小测答案:
1.解:A、主视图为长方形;
B、主视图为长方形;
C、主视图为三角形;
D、主视图为长方形.
则主视图与其他三个不相同的是C.
故选C.
2.解:由四棱柱四个侧面和上下两个底面的特征可知,A,B,D选项可以拼成一个长方体,而C选项,上底面不可能有两个,故不是长方体的展开图.
故选C.
3.解:A围成几何体时,有两个面重合,故不能围成正方体;
B、C、D均能围成正方体.
故选A.
4.解:由带有各种符号的面的特点及位置,可知只有选项D符合.
故选D.
5.解:这是一个正方体的平面展开图,共有六个面,其中“成”与面“功”相对,“预”与“祝”相对,“中”与“考”相对.
故选:B.
6.解:三棱柱的两底展开是三角形,侧面展开是三个矩形,
故答案为:①②③.
7.解:∵正视图和左视图是三角形,
∴几何体是椎体,
∵俯视图的大致轮廓是三角形,
∴该几何体是三棱锥;
∵正视图和左视图的大致轮廓是长方形,
∴该几何体是柱体,
∵俯视图是六边形,
∴该几何体是六棱柱.
8.解:能构成这个正方体的表面展开图的有:
( http: / / www.21cnjy.com )
共4种情况.
故答案为:4.
9.解:图形(1)是“田”字格,不能折成正方体;
图形(2)可折成正方体.
图形(3)是“凹”字格,不能折成正方体;
图形(4)有两个面重叠,不能折成正方体.
故答案为:(2).
10.解:如图所示:(答案不唯一)
( http: / / www.21cnjy.com )
12.解:(1)圆柱,(2)五棱柱,(3)圆锥,(4)三棱柱,
故答案为:圆柱,五棱柱,圆锥,三棱柱.
