【多媒体导学案】人教版七年级数学上册第4章第6课时《直线、射线、线段习题课》(教师版,含答案)
文档属性
| 名称 | 【多媒体导学案】人教版七年级数学上册第4章第6课时《直线、射线、线段习题课》(教师版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 164.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-13 13:36:51 | ||
图片预览




文档简介
一、学习目标 1.会统计图中直线、射线、线段的数量;2.解决线段有关的动点问题;3.解决与线段长短有关的证明问题.
二、知识回顾 填空:AD=AB+( BD )=AC+( CD ) =BC+( AB )+( CD )AD-CD=( AC )AD-BC=( AB+CD )
三、新知讲解 “四法”教你学会数线段①用基本线段数利用基本线段,依照分类讨论的方法数线段的条数时,可以做到不重不漏.问题1:数出图中线段的数量.解答:我们把AB,BC,CD,DE这四条线段成为基本线段.只含1条基本线段的有AB,BC,CD,DE,共4条;只含2条基本线段的有AC,BD,CE,共3条;只含3条基本线段的有AD,BE,共3条;只含4条基本线段的有AE,共1条;因此图中共有4+3+2+1=10条线段.②按端点数当直线上的点比较多时,按端点的位置采用分类讨论的方法数线段条数:从左到右,一次改变一个端点,只能向前,不能回头.问题2:如图,六个点O,A,B,C,D,E在同一条直线上,图中有几条线段?解答:以O为端点开始向右数,依次为OA,OB,OC,OD,OE,共5条;以A为端点开始向右数,依次为AB,AC,AD,AE,共4条;以B为端点开始向右数,依次为BC,BD,BE,共3条;以C为端点开始向右数,依次为CD,CE,共2条;以D为端点开始向右数,依次为DE,共1条;因此,图中共有5+4+3+2+1=15条线段.③利用规律计算通过上面两种方法的列式可以总结出如下规律:若基本线段有n条,则图形中共有n+(n-1)+(n-2)+…+1条线段.若端点数有m个,则图形中共有(m-1)+(m-2)+(m-3)+...+1条线段.④利用公式计算线段总条数=端点数×(端点数-1)÷2,即:线段总条数=(n为端点的个数).
四、典例探究 扫一扫,有惊喜哦!1.求图中直线、射线、线段的数量【例1】如图,A、B、C三点在同一直线上.(1)用上述字母表示的不同线段共有______条;(2)用上述字母表示的不同射线共有______条.总结:求线段条数,可以先数端点数,然后按照从端点开始依次向右数的方法数,或者直接套用公式线段总条数=(n为端点的个数).求射线条数,先看端点,依次累加各端点出发 ( http: / / www.21cnjy.com )的射线条数即可.但是如果题目要求用字母表示的不同射线条数时,要看各端点出发的射线是否能用字母表示,不能用字母表示的射线不能算.练1乘火车从A站出发,沿途经过3个车站方可 ( http: / / www.21cnjy.com )到达B站,那么在A、B两站之间需要安排不同的车票__________种.(友情提示:A站到B站与B站到A站车票不同.)2.线段上的动点问题【例2】如图,B是线段AD上一动点,沿A→ ( http: / / www.21cnjy.com )D→A以2cm/s的速度往返运动1次,C是线段BD的中点,AD=10cm,设点B运动时间为t秒(0≤t≤10).(1)当t=2时,①AB=_______cm;②求线段CD的长度.(2)用含t的代数式表示运动过程中AB的长.(3)在运动过程中,若AB中点为E,则EC的长是否变化?若不变,求出EC的长;若发生变化,请说明理由.总结:题设图形中存在一个或多个动点在线段、射线或弧线上运动的一类开放性问题,我们称为动点型问题.动点问题一定要把握运动变化的起点、终点、转折点及运动方式,采用“动中取静”的方法来解,注意研究各线段之间的等量关系.动点问题要时刻注意分类讨论.练2如图,已知数轴上点A表 ( http: / / www.21cnjy.com )示的数为6,B是数轴上一点,且AB=10,动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,(1)写出数轴上点B所表示的数;(2)点P所表示的数(用含t的代数式表示);(3)M是AP的中点,N为PB的中点, ( http: / / www.21cnjy.com )点P在运动的过程中,线段MN的长度是否发生变化?若变化,说明理由;若不变,请你画出图形,并求出线段MN的长.3.与线段长短有关的证明问题【例3】如图,点C在线段AB上,AC=8 cm,CB=6 cm,点M、N分别是AC、BC的中点.(1)求线段MN的长;(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;(3)若C在线段AB的延长线上,且 ( http: / / www.21cnjy.com )满足AC﹣BC=bcm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由;(4)你能用一句简洁的话,描述你发现的结论吗?总结:利用中点性质得出线段之间的等量关系是解题的关键.我们可以发现:无论点C在线段AB的什么位置(包括延长线),无论AC、BC的值是多少,MN都恒等于AB的一半.练3如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.(1)求线段MN的长;(2)若C为线段AB上任一点,满足AC+CB=acm,其它条件不变,你能猜想MN的长度吗?并说明理由.
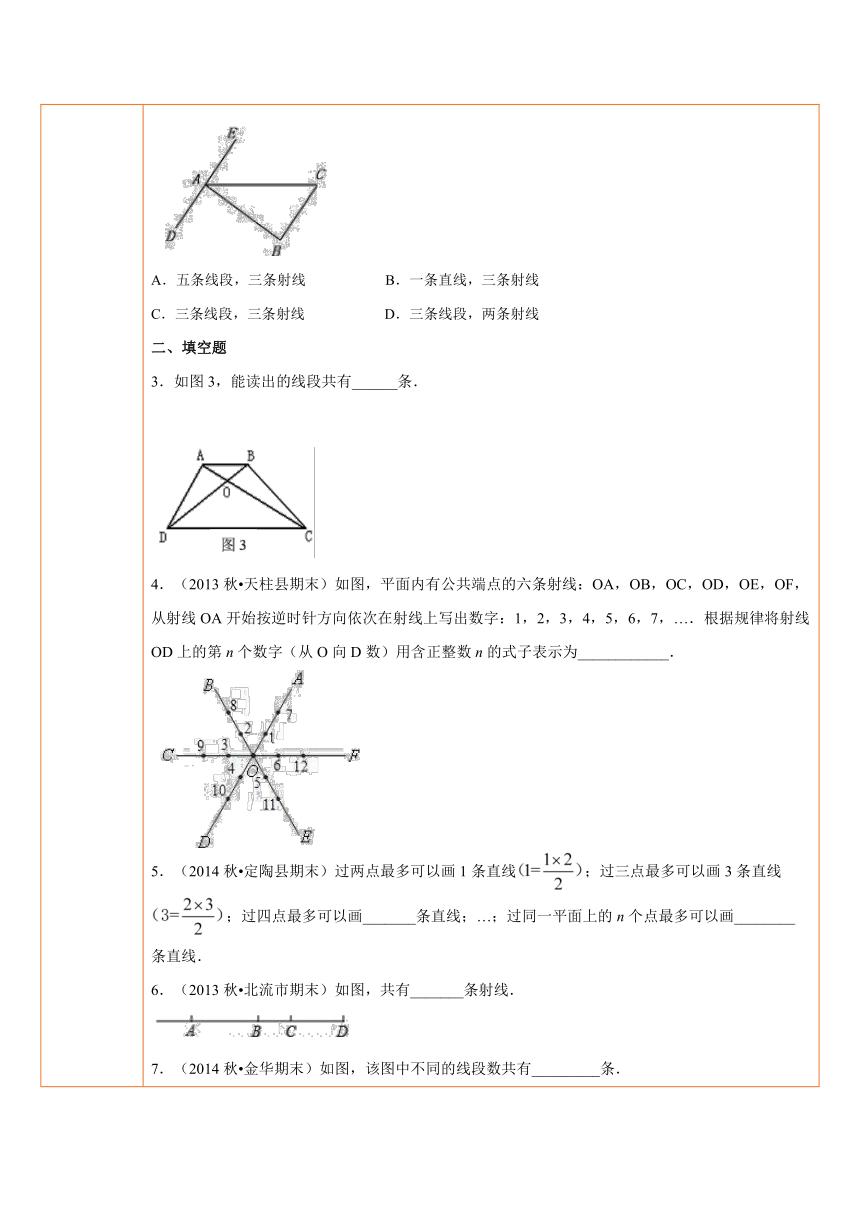
五、课后小测 一、选择题1.如下图,点A,B,C是直线l上的三个点,图中共有线段条数是( ).A.1条 B.2条 C.3条 D.4条2.如下图,线段、射线或直线的条数说法正确的是( ). ( http: / / www.21cnjy.com )A.五条线段,三条射线 B.一条直线,三条射线C.三条线段,三条射线 D.三条线段,两条射线二、填空题3.如图3,能读出的线段共有______条. ( http: / / www.21cnjy.com )4.(2013秋 天柱县期末)如图 ( http: / / www.21cnjy.com ),平面内有公共端点的六条射线:OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字:1,2,3,4,5,6,7,….根据规律将射线OD上的第n个数字(从O向D数)用含正整数n的式子表示为____________. ( http: / / www.21cnjy.com )5.(2014秋 定陶县期末)过两点最多可以画1条直线;过三点最多可以画3条直线;过四点最多可以画_______条直线;…;过同一平面上的n个点最多可以画________条直线.6.(2013秋 北流市期末)如图,共有_______条射线.7.(2014秋 金华期末)如图,该图中不同的线段数共有_________条. ( http: / / www.21cnjy.com )8.(2014秋 顺义区期末)直线AB外有C、D两个点,由点A、B、C、D可确定的直线条数是_______.三、解答题9.(2013秋 河西区期末)如图,点C在线段AB上,点M、N分别是AC、BC的中点.(1)若AC=8cm,CB=6cm,求线段MN的长;(2)若C为线段AB上任一点,满足AC+CB=a,其它条件不变,你能猜想MN的长度吗?写出你的结论并说明理由;(3)若点C在线段AB的延长线上,且满足AC ( http: / / www.21cnjy.com )﹣BC=b,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形并写出你的结论(不必说明理由).10.(2014秋 贵港期 ( http: / / www.21cnjy.com )末)如图,P是定长线段AB上一点,C、D两点同时从P、B出发分别以1cm/s和2cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上).已知C、D运动到任一时刻时,总有PD=2AC.(1)线段AP与线段AB的数量关系是:_________;(2)若Q是线段AB上一点,且AQ﹣BQ=PQ,求证:AP=PQ;(3)若C、D运动5秒后,恰好有CD=AB,此时C点停止运动,D点在线段PB上继续运动,M、N分别是CD、PD的中点,问 的值是否发生变化?若变化,请说明理由;若不变,请求出的值. ( http: / / www.21cnjy.com )11.(2013秋 高新 ( http: / / www.21cnjy.com )区期末)已知:如图,数轴上点A表示的数为6,点B表示的数为2,点C表示的数为﹣8,动点P从点A出发,沿数轴向左运动,速度为每秒1个单位长度.点M为线段BC中点,点N为线段BP中点.设运动时间为t秒.(1)线段AC的长为个单位长度;点M表示的数为________;(2)当t=5时,求线段MN的长度;(3)在整个运动过程中,求线段MN的长度.(用含t的式子表示).12.(2014秋 盐都区校级期末)( ( http: / / www.21cnjy.com )1)如下图,已知点C在线段AB上,且AC=6cm,BC=4cm,点M,N分别是AC,BC的中点,求线段MN的长度.(2)在(1)中,如果AC=acm,BC=bcm,其它条件不变,你能猜出MN的长度吗?请你用一句简洁的话表述你发现的规律.(3)对于(1)题,如果我们这样叙述它 ( http: / / www.21cnjy.com ):“已知线段AC=6cm,BC=4cm,点C在直线AB上,点M,N分别是AC,BC的中点,求MN的长度.”结果会有变化吗?如果有,求出结果.13.(2014秋 望江县期末)如图,已知数轴上A、B两点所表示的数分别为﹣2和8.(1)求线段AB的长;(2)若P为射线BA上的一点(点P ( http: / / www.21cnjy.com )不与A、B两点重合,M为PA的中点,N为PB的中点,当点P在射线BA上运动时;MN的长度是否发生改变?若不变,请你画出图形,并求出线段MN的长;若改变,请说明理由.
典例探究答案:
【例1】【解析】(1)线段的表示方法:用线段两端的字母表示,字母无先后顺序,故表示的不同线段;
(2)射线的表示法:射线的端点在前,后面加上射线上的一个字母即可,表示的不同射线.
解:(1)用上述字母表示的不同线段共有3条,分别是AB、AC、BC;
(2)射线AC、射线BC、射线BA、射线CA,故共是4条.
练1 【解析】先求出A、B两站之间共有多少条线段,根据线段的条数即可求出车票的种数.
解:
设点C、D、E是线段AB上的三个点,根据题意可得:
图中共用条线段
∵A站到B站与B站到A站车票不同.
∴A、B两站之间需要安排车票共10×2=20种
故答案为20.
【例2】【解析】(1)①根据AB=2t即可得出结论;
②先求出BD的长,再根据C是线段BD的中点即可得出CD的长;
(2)分类讨论;
(3)直接根据中点公式即可得出结论.
解:(1)①∵B是线段AD上一动点,沿A→D→A以2cm/s的速度往返运动,
∴当t=2时,AB=2×2=4cm.
故答案为:4;
②∵AD=10cm,AB=4cm,
∴BD=10﹣4=6cm,
∵C是线段BD的中点,
∴CD=BD=×6=3cm;
(2)∵B是线段AD上一动点,沿A→D→A以2cm/s的速度往返运动,
∴当0≤t≤5时,AB=2t;
当5<t≤10时,AB=10﹣(2t﹣10)=20﹣2t;
(3)不变.
∵AB中点为E,C是线段BD的中点,
∴EC=(AB+BD)=AD=×10=5(cm).
练2【解析】(1)由已知得OA=6,则OB=AB﹣OA=4,因为点B在原点左边,从而写出数轴上点B所表示的数;
(2)动点P从点A出发,运动时间为t(t>0)秒,所以运动的单位长度为6t,因为沿数轴向左匀速运动,所以点P所表示的数是6﹣6t;
(3)可分两种情况,通过计算表示出线段MN的长都为AB,所以得出结论线段MN的长度不发生变化.
解:(1)∵数轴上点A表示的数为6,
∴OA=6,
则OB=AB﹣OA=4,
点B在原点左边,
所以数轴上点B所表示的数为﹣4,
故答案为:﹣4;
(2)点P运动t秒的长度为6t,
∵动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,
∴P所表示的数为:6﹣6t,
故答案为:6﹣6t;
(3)线段MN的长度不发生变化,
理由:
分两种情况:
①当点P在A、B两点之间运动时,如图
MN=MP+NP=BP+PA=AB=5
②当点P运动到B的左边时,如图
MN=MP﹣NP=AP﹣PB=AB=5
综上所述,线段MN的长度不发生变化,其值为5.
【例3】【解析】(1)根据M、N分别是A ( http: / / www.21cnjy.com )C、BC的中点,我们可得出MC、NC分别是AC、BC的一半,那么MC、CN的和就应该是AC、BC和的一半,也就是说MN是AB的一半,有了AC、CB的值,那么就有了AB的值,也就能求出MN的值了;
(2)方法同(1)只不过AC、BC的值换成了AC+CB=a cm,其他步骤是一样的;
(3)当C在线段AB的延长线上时,根 ( http: / / www.21cnjy.com )据M、N分别是AC、BC的中点,我们可得出MC、NC分别是AC、BC的一半.于是,MC、NC的差就应该是AC、BC的差的一半,也就是说MN是AC﹣BC即AB的一半.有AC﹣BC的值,MN也就能求出来了;
(4)综合上面我们可发现,无论C在线段AB的什么位置(包括延长线),无论AC、BC的值是多少,MN都恒等于AB的一半.
解:(1)
∵M、N分别是AC、BC的中点,
∴MC=AC,CN=BC,
∵MN=MC+CN,AB=AC+BC,
∴MN=AB=7cm;
(2)MN=,
∵M、N分别是AC、BC的中点,
∴MC=AC,CN=BC,
又∵MN=MC+CN,AB=AC+BC,
∴MN=(AC+BC)=;
(3)∵M、N分别是AC、BC的中点,
∴MC=AC,NC=BC,
又∵AB=AC﹣BC,NM=MC﹣NC,
∴MN=(AC﹣BC)=;
(4)如图,只要满足点C在线段AB所在直线上,点M、N分别是AC、BC的中点.那么MN就等于AB的一半.
练3 【解析】(1)根据“点M、N分别是AC、BC的中点”,先求出MC、CN的长度,再利用MN=CM+CN即可求出MN的长度;
(2)与(1)同理,先用AC、BC表示出MC、CN,MN的长度就等于AC与BC长度和的一半.
解:(1)∵点M、N分别是AC、BC的中点,
∴CM=AC=4cm,CN=BC=3cm,
∴MN=CM+CN=4+3=7cm;
(2)同(1)可得CM=AC,CN=BC,
∴MN=CM+CN=AC+BC=(AC+BC)=a.
课后小测答案:
一、选择题
1.C
2.D
二、填空题
3.10
4.【解析】写出线段上的数据,再寻找并发现规律.
解:射线OD上的第1个数字为4,
第2个为旋转一周后,是第10个,
第3个,再旋转一周,转过了6个数字;
…
由此发现规律:每两个数字之差为6,那么射线OD上的第n个数字表示为6n﹣2.
5.【解析】根据已知所反映的规律1= ,3=,6=得出即可.
解:过过四点最多可以画=6条直线,
过同一平面上的n个点最多可以画条直线.
故答案为:6,.
6.【解析】根据射线的定义解答.
解:分别以点A、B、C、D为端点向左各有一条射线,
共4条.
故答案为:4.
7.【解析】根据图形数出线段的条数即可,注意不要重复和漏数.
解:线段AB,线段AD,线段BC,线段DC,线段AC,线段BD,共6条,
故答案为:6.
8.【解析】在明确两点确定一条直线的前提下,根据点的位置分类确定直线的条数.
解:当A、B、C、D4个点有3点在一条直线上时,可以确定4条直线,
当4点两两在一直线上时能确定6条直线.
故答案为:6或4.
三、解答题
9.【解析】(1)据“点M、N分别是AC、BC的中点”,先求出MC、CN的长度,再利用MN=CM+CN即可求出MN的长度即可.
(2)据题意画出图形即可得出答案.
(3)据题意画出图形即可得出答案.
解:(1)点M、N分别是AC、BC的中点,
∴CM=AC=4cm,
CN=BC=3cm,
∴MN=CM+CN=4+3=7cm.
所以线段MN的长为7cm.
(2)MN的长度等于a,
根据图形和题意可得:MN=MC+CN=AC+BC=(AC+BC)=a.
(3)MN的长度等于b,
根据图形和题意可得:
MN=MC﹣NC=AC﹣BC=(AC﹣BC)=b.
10.【解析】(1)根据BD=2PC可知PD=2AC,故可得出BD+PD=2(PC+AC),即PB=2AP,所以点P在线段AB上的处;
(2)由题意得AQ>BQ,故AQ=AP+PQ,再根据AQ﹣BQ=PQ,可知AQ=BQ+PQ,故AP=BQ,由(1)得,AP=AB,故PQ=AB﹣AP﹣BQ=AB;
(3)当C点停止运动时,有CD=AB,故AC+BD=AB,所以AP﹣PC+BD=AB,再由AP=AB,PC=5cm,BD=10cm,所以AB﹣5+10=AB,解得AB=30cm,再根据M是CD中点,N是PD中点可得出MN的长,进而可得出结论.
解:(1)根据C、D的运动速度知:BD=2PC,
∵PD=2AC,
∴BD+PD=2(PC+AC),即PB=2AP,
∴点P在线段AB上的处,即AB=3AP.
故答案为:AB=3AP;
(2)证明:如图1,由题意得AQ>BQ,
∴AQ=AP+PQ,
又∵AQ﹣BQ=PQ,
∴AQ=BQ+PQ,
∴AP=BQ.由(1)得,AP=AB,
∴PQ=AB﹣AP﹣BQ=AB.
(3)的值不变.
理由:如图2,当C点停止运动时,有CD=AB,
∴AC+BD=AB,
∴AP﹣PC+BD=AB,
∵AP=AB,PC=5cm,BD=10cm,
∴AB﹣5+10=AB,
解得AB=30cm.
∵M是CD中点,N是PD中点,
∴MN=MD﹣ND=CD﹣PD=CP=cm,
∴=.
11.【解析】(1)根据两点间的距离公式可得AC=6﹣(﹣8),根据中点坐标公式可得M点表示的数为﹣8+[2﹣(﹣8)];
(2)当t=5时,可得P表示的数,再根据中点坐标公式可得N点表示的数,再根据两点间的距离公式可得线段MN的长度;
(3)分①当点P在点A、B两点之间运动时,②当点P运动到点B的左侧时,利用中点的定义和线段的和差求出MN的长即可.
解:(1)线段AC的长为AC=6﹣(﹣8)=14个单位长度;
点M表示的数为﹣8+[2﹣(﹣8)]=﹣3;
(2)当t=5时,点P表示的数为6﹣5×1=1,
点N表示的数为2﹣[2﹣1]=1.5,
线段MN的长度为1.5﹣(﹣3)=4.5;
(3)①当点P在点A、B两点之间运动时,点P表示的数为6﹣t,
点N表示的数为2+[(6﹣t)﹣2]=4﹣t,
线段MN的长度为4﹣t﹣(﹣3)=7﹣t;
②当点P运动到点B的左侧时,点P表示的数为6﹣t,点N表示的数为2﹣[2﹣(6﹣t)]=4﹣t,
线段MN的长度为|4﹣t﹣(﹣3)|=|7﹣t|.
故答案为:14,﹣3.
12.【解析】(1)(2)在一条直线或 ( http: / / www.21cnjy.com )线段上的线段的加减运算和倍数运算,首先明确线段间的相互关系,最好准确画出几何图形,再根据题意进行计算;
(3)会出现两种情况:①点C在线段AB上;②点C在AB或BA的延长线上.不要漏解.
解:(1)∵AC=6cm,BC=4cm,点M,N分别是AC,BC的中点,
∴MN=(AC+CB)=×10=5cm;
(2)MN=,直线上相邻两线段中点间的距离为两线段长度和的一半;
(3)如图,有变化,会出现两种情况:
①当点C在线段AB上时,MN=(AC+BC)=5cm;
②当点C在AB或BA的延长线上时,MN=(AC﹣BC)=1cm.
13.【解析】(1)根据数轴与绝对值知,AB=|OB|+|OA|;
(2)分两种情况进行讨论:①当点P在A、B两点之间运动时;②当点P在点A的左侧运动时.
解:(1)∵A,B两点所表示的数分别为﹣2和8,
∴0A=2,OB=8∴AB=OA+OB=lO.(5分)
(2)线段MN的长度不发生变化,其值为5.分下面两种情况:
①当点P在A、B两点之间运动时(如图甲).
MN=MP+NP=AP+BP=AB=5(3分)
②当点P在点A的左侧运动时(如图乙).
MN=NP﹣MP=BP﹣AP=AB=5
综上所述,线段MN的长度不发生变化,其值为5.
二、知识回顾 填空:AD=AB+( BD )=AC+( CD ) =BC+( AB )+( CD )AD-CD=( AC )AD-BC=( AB+CD )
三、新知讲解 “四法”教你学会数线段①用基本线段数利用基本线段,依照分类讨论的方法数线段的条数时,可以做到不重不漏.问题1:数出图中线段的数量.解答:我们把AB,BC,CD,DE这四条线段成为基本线段.只含1条基本线段的有AB,BC,CD,DE,共4条;只含2条基本线段的有AC,BD,CE,共3条;只含3条基本线段的有AD,BE,共3条;只含4条基本线段的有AE,共1条;因此图中共有4+3+2+1=10条线段.②按端点数当直线上的点比较多时,按端点的位置采用分类讨论的方法数线段条数:从左到右,一次改变一个端点,只能向前,不能回头.问题2:如图,六个点O,A,B,C,D,E在同一条直线上,图中有几条线段?解答:以O为端点开始向右数,依次为OA,OB,OC,OD,OE,共5条;以A为端点开始向右数,依次为AB,AC,AD,AE,共4条;以B为端点开始向右数,依次为BC,BD,BE,共3条;以C为端点开始向右数,依次为CD,CE,共2条;以D为端点开始向右数,依次为DE,共1条;因此,图中共有5+4+3+2+1=15条线段.③利用规律计算通过上面两种方法的列式可以总结出如下规律:若基本线段有n条,则图形中共有n+(n-1)+(n-2)+…+1条线段.若端点数有m个,则图形中共有(m-1)+(m-2)+(m-3)+...+1条线段.④利用公式计算线段总条数=端点数×(端点数-1)÷2,即:线段总条数=(n为端点的个数).
四、典例探究 扫一扫,有惊喜哦!1.求图中直线、射线、线段的数量【例1】如图,A、B、C三点在同一直线上.(1)用上述字母表示的不同线段共有______条;(2)用上述字母表示的不同射线共有______条.总结:求线段条数,可以先数端点数,然后按照从端点开始依次向右数的方法数,或者直接套用公式线段总条数=(n为端点的个数).求射线条数,先看端点,依次累加各端点出发 ( http: / / www.21cnjy.com )的射线条数即可.但是如果题目要求用字母表示的不同射线条数时,要看各端点出发的射线是否能用字母表示,不能用字母表示的射线不能算.练1乘火车从A站出发,沿途经过3个车站方可 ( http: / / www.21cnjy.com )到达B站,那么在A、B两站之间需要安排不同的车票__________种.(友情提示:A站到B站与B站到A站车票不同.)2.线段上的动点问题【例2】如图,B是线段AD上一动点,沿A→ ( http: / / www.21cnjy.com )D→A以2cm/s的速度往返运动1次,C是线段BD的中点,AD=10cm,设点B运动时间为t秒(0≤t≤10).(1)当t=2时,①AB=_______cm;②求线段CD的长度.(2)用含t的代数式表示运动过程中AB的长.(3)在运动过程中,若AB中点为E,则EC的长是否变化?若不变,求出EC的长;若发生变化,请说明理由.总结:题设图形中存在一个或多个动点在线段、射线或弧线上运动的一类开放性问题,我们称为动点型问题.动点问题一定要把握运动变化的起点、终点、转折点及运动方式,采用“动中取静”的方法来解,注意研究各线段之间的等量关系.动点问题要时刻注意分类讨论.练2如图,已知数轴上点A表 ( http: / / www.21cnjy.com )示的数为6,B是数轴上一点,且AB=10,动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,(1)写出数轴上点B所表示的数;(2)点P所表示的数(用含t的代数式表示);(3)M是AP的中点,N为PB的中点, ( http: / / www.21cnjy.com )点P在运动的过程中,线段MN的长度是否发生变化?若变化,说明理由;若不变,请你画出图形,并求出线段MN的长.3.与线段长短有关的证明问题【例3】如图,点C在线段AB上,AC=8 cm,CB=6 cm,点M、N分别是AC、BC的中点.(1)求线段MN的长;(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;(3)若C在线段AB的延长线上,且 ( http: / / www.21cnjy.com )满足AC﹣BC=bcm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由;(4)你能用一句简洁的话,描述你发现的结论吗?总结:利用中点性质得出线段之间的等量关系是解题的关键.我们可以发现:无论点C在线段AB的什么位置(包括延长线),无论AC、BC的值是多少,MN都恒等于AB的一半.练3如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.(1)求线段MN的长;(2)若C为线段AB上任一点,满足AC+CB=acm,其它条件不变,你能猜想MN的长度吗?并说明理由.
五、课后小测 一、选择题1.如下图,点A,B,C是直线l上的三个点,图中共有线段条数是( ).A.1条 B.2条 C.3条 D.4条2.如下图,线段、射线或直线的条数说法正确的是( ). ( http: / / www.21cnjy.com )A.五条线段,三条射线 B.一条直线,三条射线C.三条线段,三条射线 D.三条线段,两条射线二、填空题3.如图3,能读出的线段共有______条. ( http: / / www.21cnjy.com )4.(2013秋 天柱县期末)如图 ( http: / / www.21cnjy.com ),平面内有公共端点的六条射线:OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字:1,2,3,4,5,6,7,….根据规律将射线OD上的第n个数字(从O向D数)用含正整数n的式子表示为____________. ( http: / / www.21cnjy.com )5.(2014秋 定陶县期末)过两点最多可以画1条直线;过三点最多可以画3条直线;过四点最多可以画_______条直线;…;过同一平面上的n个点最多可以画________条直线.6.(2013秋 北流市期末)如图,共有_______条射线.7.(2014秋 金华期末)如图,该图中不同的线段数共有_________条. ( http: / / www.21cnjy.com )8.(2014秋 顺义区期末)直线AB外有C、D两个点,由点A、B、C、D可确定的直线条数是_______.三、解答题9.(2013秋 河西区期末)如图,点C在线段AB上,点M、N分别是AC、BC的中点.(1)若AC=8cm,CB=6cm,求线段MN的长;(2)若C为线段AB上任一点,满足AC+CB=a,其它条件不变,你能猜想MN的长度吗?写出你的结论并说明理由;(3)若点C在线段AB的延长线上,且满足AC ( http: / / www.21cnjy.com )﹣BC=b,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形并写出你的结论(不必说明理由).10.(2014秋 贵港期 ( http: / / www.21cnjy.com )末)如图,P是定长线段AB上一点,C、D两点同时从P、B出发分别以1cm/s和2cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上).已知C、D运动到任一时刻时,总有PD=2AC.(1)线段AP与线段AB的数量关系是:_________;(2)若Q是线段AB上一点,且AQ﹣BQ=PQ,求证:AP=PQ;(3)若C、D运动5秒后,恰好有CD=AB,此时C点停止运动,D点在线段PB上继续运动,M、N分别是CD、PD的中点,问 的值是否发生变化?若变化,请说明理由;若不变,请求出的值. ( http: / / www.21cnjy.com )11.(2013秋 高新 ( http: / / www.21cnjy.com )区期末)已知:如图,数轴上点A表示的数为6,点B表示的数为2,点C表示的数为﹣8,动点P从点A出发,沿数轴向左运动,速度为每秒1个单位长度.点M为线段BC中点,点N为线段BP中点.设运动时间为t秒.(1)线段AC的长为个单位长度;点M表示的数为________;(2)当t=5时,求线段MN的长度;(3)在整个运动过程中,求线段MN的长度.(用含t的式子表示).12.(2014秋 盐都区校级期末)( ( http: / / www.21cnjy.com )1)如下图,已知点C在线段AB上,且AC=6cm,BC=4cm,点M,N分别是AC,BC的中点,求线段MN的长度.(2)在(1)中,如果AC=acm,BC=bcm,其它条件不变,你能猜出MN的长度吗?请你用一句简洁的话表述你发现的规律.(3)对于(1)题,如果我们这样叙述它 ( http: / / www.21cnjy.com ):“已知线段AC=6cm,BC=4cm,点C在直线AB上,点M,N分别是AC,BC的中点,求MN的长度.”结果会有变化吗?如果有,求出结果.13.(2014秋 望江县期末)如图,已知数轴上A、B两点所表示的数分别为﹣2和8.(1)求线段AB的长;(2)若P为射线BA上的一点(点P ( http: / / www.21cnjy.com )不与A、B两点重合,M为PA的中点,N为PB的中点,当点P在射线BA上运动时;MN的长度是否发生改变?若不变,请你画出图形,并求出线段MN的长;若改变,请说明理由.
典例探究答案:
【例1】【解析】(1)线段的表示方法:用线段两端的字母表示,字母无先后顺序,故表示的不同线段;
(2)射线的表示法:射线的端点在前,后面加上射线上的一个字母即可,表示的不同射线.
解:(1)用上述字母表示的不同线段共有3条,分别是AB、AC、BC;
(2)射线AC、射线BC、射线BA、射线CA,故共是4条.
练1 【解析】先求出A、B两站之间共有多少条线段,根据线段的条数即可求出车票的种数.
解:
设点C、D、E是线段AB上的三个点,根据题意可得:
图中共用条线段
∵A站到B站与B站到A站车票不同.
∴A、B两站之间需要安排车票共10×2=20种
故答案为20.
【例2】【解析】(1)①根据AB=2t即可得出结论;
②先求出BD的长,再根据C是线段BD的中点即可得出CD的长;
(2)分类讨论;
(3)直接根据中点公式即可得出结论.
解:(1)①∵B是线段AD上一动点,沿A→D→A以2cm/s的速度往返运动,
∴当t=2时,AB=2×2=4cm.
故答案为:4;
②∵AD=10cm,AB=4cm,
∴BD=10﹣4=6cm,
∵C是线段BD的中点,
∴CD=BD=×6=3cm;
(2)∵B是线段AD上一动点,沿A→D→A以2cm/s的速度往返运动,
∴当0≤t≤5时,AB=2t;
当5<t≤10时,AB=10﹣(2t﹣10)=20﹣2t;
(3)不变.
∵AB中点为E,C是线段BD的中点,
∴EC=(AB+BD)=AD=×10=5(cm).
练2【解析】(1)由已知得OA=6,则OB=AB﹣OA=4,因为点B在原点左边,从而写出数轴上点B所表示的数;
(2)动点P从点A出发,运动时间为t(t>0)秒,所以运动的单位长度为6t,因为沿数轴向左匀速运动,所以点P所表示的数是6﹣6t;
(3)可分两种情况,通过计算表示出线段MN的长都为AB,所以得出结论线段MN的长度不发生变化.
解:(1)∵数轴上点A表示的数为6,
∴OA=6,
则OB=AB﹣OA=4,
点B在原点左边,
所以数轴上点B所表示的数为﹣4,
故答案为:﹣4;
(2)点P运动t秒的长度为6t,
∵动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,
∴P所表示的数为:6﹣6t,
故答案为:6﹣6t;
(3)线段MN的长度不发生变化,
理由:
分两种情况:
①当点P在A、B两点之间运动时,如图
MN=MP+NP=BP+PA=AB=5
②当点P运动到B的左边时,如图
MN=MP﹣NP=AP﹣PB=AB=5
综上所述,线段MN的长度不发生变化,其值为5.
【例3】【解析】(1)根据M、N分别是A ( http: / / www.21cnjy.com )C、BC的中点,我们可得出MC、NC分别是AC、BC的一半,那么MC、CN的和就应该是AC、BC和的一半,也就是说MN是AB的一半,有了AC、CB的值,那么就有了AB的值,也就能求出MN的值了;
(2)方法同(1)只不过AC、BC的值换成了AC+CB=a cm,其他步骤是一样的;
(3)当C在线段AB的延长线上时,根 ( http: / / www.21cnjy.com )据M、N分别是AC、BC的中点,我们可得出MC、NC分别是AC、BC的一半.于是,MC、NC的差就应该是AC、BC的差的一半,也就是说MN是AC﹣BC即AB的一半.有AC﹣BC的值,MN也就能求出来了;
(4)综合上面我们可发现,无论C在线段AB的什么位置(包括延长线),无论AC、BC的值是多少,MN都恒等于AB的一半.
解:(1)
∵M、N分别是AC、BC的中点,
∴MC=AC,CN=BC,
∵MN=MC+CN,AB=AC+BC,
∴MN=AB=7cm;
(2)MN=,
∵M、N分别是AC、BC的中点,
∴MC=AC,CN=BC,
又∵MN=MC+CN,AB=AC+BC,
∴MN=(AC+BC)=;
(3)∵M、N分别是AC、BC的中点,
∴MC=AC,NC=BC,
又∵AB=AC﹣BC,NM=MC﹣NC,
∴MN=(AC﹣BC)=;
(4)如图,只要满足点C在线段AB所在直线上,点M、N分别是AC、BC的中点.那么MN就等于AB的一半.
练3 【解析】(1)根据“点M、N分别是AC、BC的中点”,先求出MC、CN的长度,再利用MN=CM+CN即可求出MN的长度;
(2)与(1)同理,先用AC、BC表示出MC、CN,MN的长度就等于AC与BC长度和的一半.
解:(1)∵点M、N分别是AC、BC的中点,
∴CM=AC=4cm,CN=BC=3cm,
∴MN=CM+CN=4+3=7cm;
(2)同(1)可得CM=AC,CN=BC,
∴MN=CM+CN=AC+BC=(AC+BC)=a.
课后小测答案:
一、选择题
1.C
2.D
二、填空题
3.10
4.【解析】写出线段上的数据,再寻找并发现规律.
解:射线OD上的第1个数字为4,
第2个为旋转一周后,是第10个,
第3个,再旋转一周,转过了6个数字;
…
由此发现规律:每两个数字之差为6,那么射线OD上的第n个数字表示为6n﹣2.
5.【解析】根据已知所反映的规律1= ,3=,6=得出即可.
解:过过四点最多可以画=6条直线,
过同一平面上的n个点最多可以画条直线.
故答案为:6,.
6.【解析】根据射线的定义解答.
解:分别以点A、B、C、D为端点向左各有一条射线,
共4条.
故答案为:4.
7.【解析】根据图形数出线段的条数即可,注意不要重复和漏数.
解:线段AB,线段AD,线段BC,线段DC,线段AC,线段BD,共6条,
故答案为:6.
8.【解析】在明确两点确定一条直线的前提下,根据点的位置分类确定直线的条数.
解:当A、B、C、D4个点有3点在一条直线上时,可以确定4条直线,
当4点两两在一直线上时能确定6条直线.
故答案为:6或4.
三、解答题
9.【解析】(1)据“点M、N分别是AC、BC的中点”,先求出MC、CN的长度,再利用MN=CM+CN即可求出MN的长度即可.
(2)据题意画出图形即可得出答案.
(3)据题意画出图形即可得出答案.
解:(1)点M、N分别是AC、BC的中点,
∴CM=AC=4cm,
CN=BC=3cm,
∴MN=CM+CN=4+3=7cm.
所以线段MN的长为7cm.
(2)MN的长度等于a,
根据图形和题意可得:MN=MC+CN=AC+BC=(AC+BC)=a.
(3)MN的长度等于b,
根据图形和题意可得:
MN=MC﹣NC=AC﹣BC=(AC﹣BC)=b.
10.【解析】(1)根据BD=2PC可知PD=2AC,故可得出BD+PD=2(PC+AC),即PB=2AP,所以点P在线段AB上的处;
(2)由题意得AQ>BQ,故AQ=AP+PQ,再根据AQ﹣BQ=PQ,可知AQ=BQ+PQ,故AP=BQ,由(1)得,AP=AB,故PQ=AB﹣AP﹣BQ=AB;
(3)当C点停止运动时,有CD=AB,故AC+BD=AB,所以AP﹣PC+BD=AB,再由AP=AB,PC=5cm,BD=10cm,所以AB﹣5+10=AB,解得AB=30cm,再根据M是CD中点,N是PD中点可得出MN的长,进而可得出结论.
解:(1)根据C、D的运动速度知:BD=2PC,
∵PD=2AC,
∴BD+PD=2(PC+AC),即PB=2AP,
∴点P在线段AB上的处,即AB=3AP.
故答案为:AB=3AP;
(2)证明:如图1,由题意得AQ>BQ,
∴AQ=AP+PQ,
又∵AQ﹣BQ=PQ,
∴AQ=BQ+PQ,
∴AP=BQ.由(1)得,AP=AB,
∴PQ=AB﹣AP﹣BQ=AB.
(3)的值不变.
理由:如图2,当C点停止运动时,有CD=AB,
∴AC+BD=AB,
∴AP﹣PC+BD=AB,
∵AP=AB,PC=5cm,BD=10cm,
∴AB﹣5+10=AB,
解得AB=30cm.
∵M是CD中点,N是PD中点,
∴MN=MD﹣ND=CD﹣PD=CP=cm,
∴=.
11.【解析】(1)根据两点间的距离公式可得AC=6﹣(﹣8),根据中点坐标公式可得M点表示的数为﹣8+[2﹣(﹣8)];
(2)当t=5时,可得P表示的数,再根据中点坐标公式可得N点表示的数,再根据两点间的距离公式可得线段MN的长度;
(3)分①当点P在点A、B两点之间运动时,②当点P运动到点B的左侧时,利用中点的定义和线段的和差求出MN的长即可.
解:(1)线段AC的长为AC=6﹣(﹣8)=14个单位长度;
点M表示的数为﹣8+[2﹣(﹣8)]=﹣3;
(2)当t=5时,点P表示的数为6﹣5×1=1,
点N表示的数为2﹣[2﹣1]=1.5,
线段MN的长度为1.5﹣(﹣3)=4.5;
(3)①当点P在点A、B两点之间运动时,点P表示的数为6﹣t,
点N表示的数为2+[(6﹣t)﹣2]=4﹣t,
线段MN的长度为4﹣t﹣(﹣3)=7﹣t;
②当点P运动到点B的左侧时,点P表示的数为6﹣t,点N表示的数为2﹣[2﹣(6﹣t)]=4﹣t,
线段MN的长度为|4﹣t﹣(﹣3)|=|7﹣t|.
故答案为:14,﹣3.
12.【解析】(1)(2)在一条直线或 ( http: / / www.21cnjy.com )线段上的线段的加减运算和倍数运算,首先明确线段间的相互关系,最好准确画出几何图形,再根据题意进行计算;
(3)会出现两种情况:①点C在线段AB上;②点C在AB或BA的延长线上.不要漏解.
解:(1)∵AC=6cm,BC=4cm,点M,N分别是AC,BC的中点,
∴MN=(AC+CB)=×10=5cm;
(2)MN=,直线上相邻两线段中点间的距离为两线段长度和的一半;
(3)如图,有变化,会出现两种情况:
①当点C在线段AB上时,MN=(AC+BC)=5cm;
②当点C在AB或BA的延长线上时,MN=(AC﹣BC)=1cm.
13.【解析】(1)根据数轴与绝对值知,AB=|OB|+|OA|;
(2)分两种情况进行讨论:①当点P在A、B两点之间运动时;②当点P在点A的左侧运动时.
解:(1)∵A,B两点所表示的数分别为﹣2和8,
∴0A=2,OB=8∴AB=OA+OB=lO.(5分)
(2)线段MN的长度不发生变化,其值为5.分下面两种情况:
①当点P在A、B两点之间运动时(如图甲).
MN=MP+NP=AP+BP=AB=5(3分)
②当点P在点A的左侧运动时(如图乙).
MN=NP﹣MP=BP﹣AP=AB=5
综上所述,线段MN的长度不发生变化,其值为5.
