【多媒体导学案】人教版七年级数学上册第4章第10课时《角的运算习题课》(教师版,含答案)
文档属性
| 名称 | 【多媒体导学案】人教版七年级数学上册第4章第10课时《角的运算习题课》(教师版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 199.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-13 13:44:38 | ||
图片预览


文档简介
一、学习目标 1.会用一副三角板拼角;2.会计算几何图形或三角板中的角度;3.解决角n等分线的综合计算问题;
二、知识回顾 1. 三角板的认识一副三角板的各个角分别是多少度? 30°、60°、90°;45°、45°、90° 2. 角的平分线从一个角的 顶点 出发,把这个角分成 ( http: / / www.21cnjy.com ) 大小相等 的两个角的射线,叫做这个角的平分线.类似地,还有角的三等分线等.如下图中的OB、OC是∠AOD的三等分线. ( http: / / www.21cnjy.com )
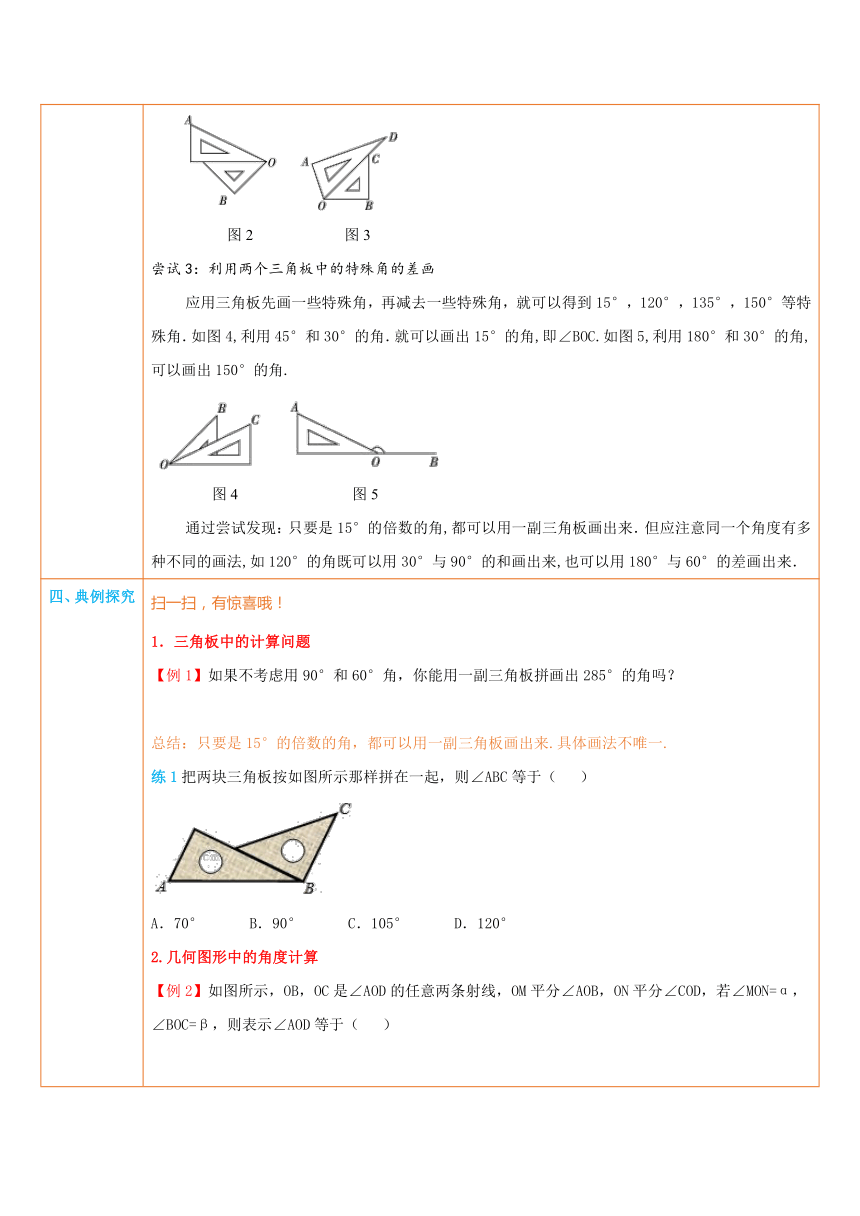
三、新知讲解 三角板中的计算问题如图,一副三角板共 ( http: / / www.21cnjy.com )有6个角,且有30°,4 ( http: / / www.21cnjy.com )5°,60°,90°四种角度,如果只用一副三角板,你能作出哪些不同大小的角?看起来这个问题似乎很简单,但是,若仔细地思考一番,想要找到问题的答案,也并非容易. ( http: / / www.21cnjy.com )尝试1:只用一个三角板画用1个三角板可以画出30°,45°,60°,90°,180°这几个特殊角.尝试2:利用两个三角板中的特殊角的和画用2个三角板的两个角,并将角叠加,就可以得 ( http: / / www.21cnjy.com )到75°,105°,120°,150°等特殊角.如图2,将30°角与45°角拼在一起可以画出75°的角,即∠AOB.如图3,将60°角与45°角拼在一起,可以画出105°的角,即∠AOB. ( http: / / www.21cnjy.com )图2 图3尝试3:利用两个三角板中的特殊角的差画应用三角板先画一些特殊角, ( http: / / www.21cnjy.com )再减去一些特殊角,就可以得到15°,120°,135°,150°等特殊角.如图4,利用45°和30°的角.就可以画出15°的角,即∠BOC.如图5,利用180°和30°的角,可以画出150°的角. ( http: / / www.21cnjy.com )图4 图5通过尝试发现:只要是15°的倍数的角,都可以用一副三角板画出来.但应注意同一个角度有多种不同的画法,如120°的角既可以用30°与90°的和画出来,也可以用180°与60°的差画出来.
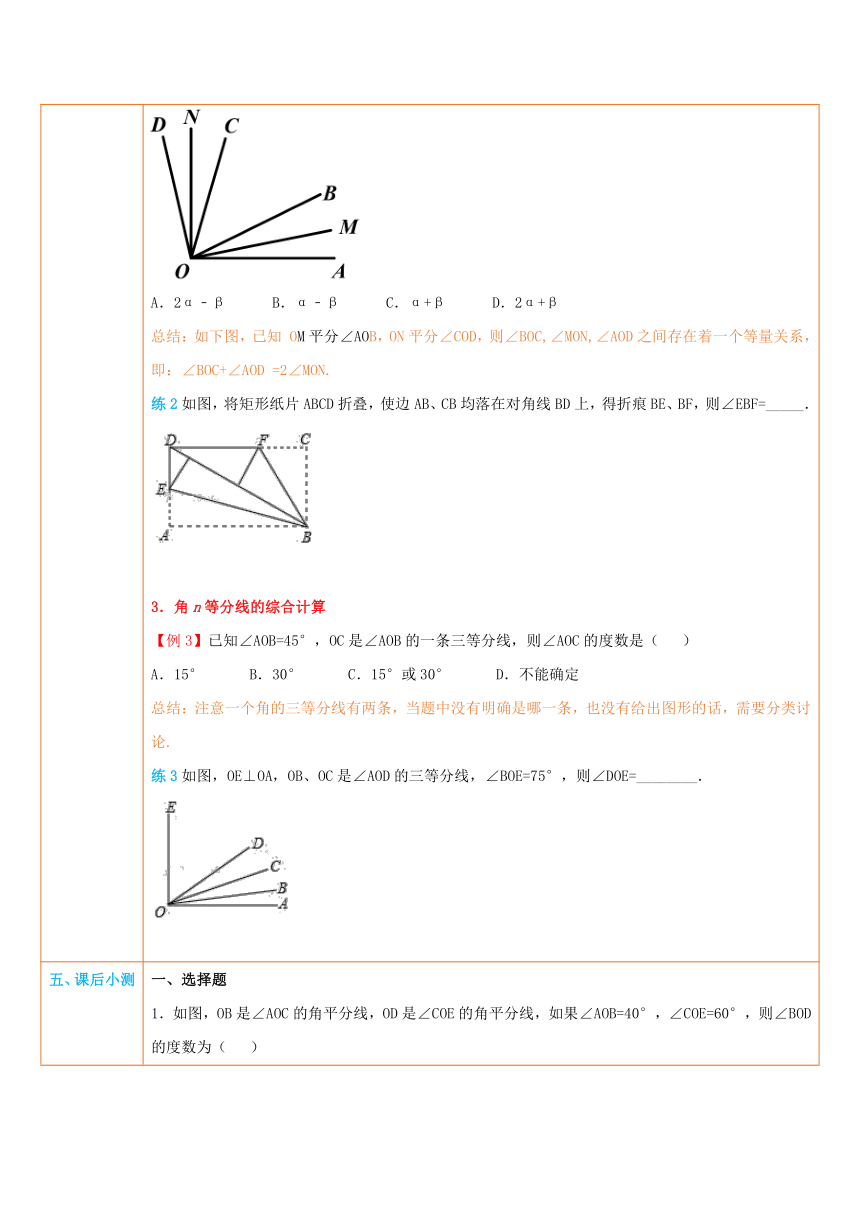
四、典例探究 扫一扫,有惊喜哦!1.三角板中的计算问题【例1】如果不考虑用90°和60°角,你能用一副三角板拼画出285°的角吗?总结:只要是15°的倍数的角,都可以用一副三角板画出来.具体画法不唯一.练1把两块三角板按如图所示那样拼在一起,则∠ABC等于( ) ( http: / / www.21cnjy.com )A.70° B.90° C.105° D.120°2.几何图形中的角度计算【例2】如图所示,OB,OC是∠A ( http: / / www.21cnjy.com )OD的任意两条射线,OM平分∠AOB,ON平分∠COD,若∠MON=α,∠BOC=β,则表示∠AOD等于( ) ( http: / / www.21cnjy.com )A.2α﹣β B.α﹣β C.α+β D.2α+β总结:如下图,已知 OM平分∠AO ( http: / / www.21cnjy.com )B,ON平分∠COD,则∠BOC,∠MON,∠AOD之间存在着一个等量关系,即:∠BOC+∠AOD =2∠MON.练2如图,将矩形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF=_____. ( http: / / www.21cnjy.com )3.角n等分线的综合计算【例3】已知∠AOB=45°,OC是∠AOB的一条三等分线,则∠AOC的度数是( )A.15° B.30° C.15°或30° D.不能确定总结:注意一个角的三等分线有两条,当题中没有明确是哪一条,也没有给出图形的话,需要分类讨论.练3如图,OE⊥OA,OB、OC是∠AOD的三等分线,∠BOE=75°,则∠DOE=________. ( http: / / www.21cnjy.com )
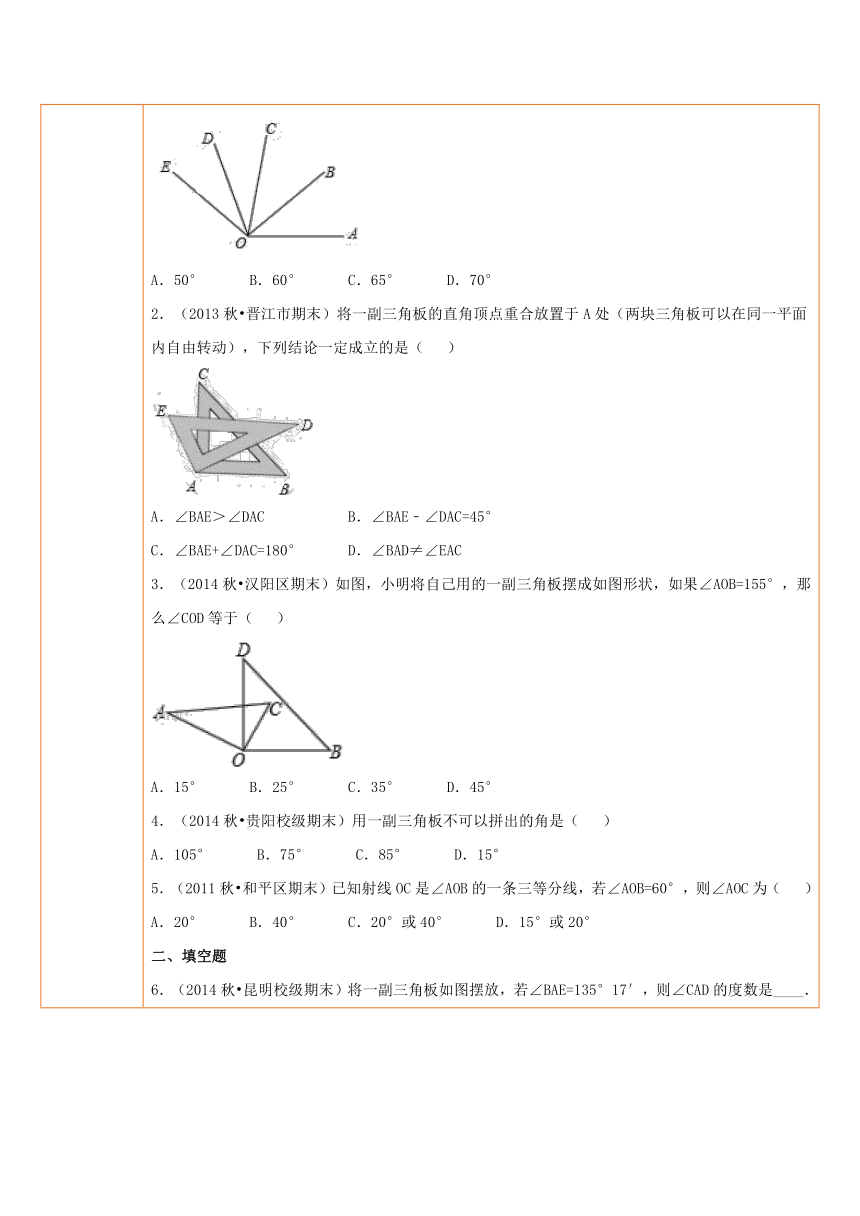
五、课后小测 一、选择题1.如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为( ) ( http: / / www.21cnjy.com )A.50° B.60° C.65° D.70°2.(2013秋 晋江市期末)将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),下列结论一定成立的是( ) ( http: / / www.21cnjy.com )A.∠BAE>∠DAC B.∠BAE﹣∠DAC=45°C.∠BAE+∠DAC=180° D.∠BAD≠∠EAC3.(2014秋 汉阳区期末)如图,小明将自己用的一副三角板摆成如图形状,如果∠AOB=155°,那么∠COD等于( ) ( http: / / www.21cnjy.com )A.15° B.25° C.35° D.45°4.(2014秋 贵阳校级期末)用一副三角板不可以拼出的角是( )A.105° B.75° C.85° D.15°5.(2011秋 和平区期末)已知射线OC是∠AOB的一条三等分线,若∠AOB=60°,则∠AOC为( )A.20° B.40° C.20°或40° D.15°或20°二、填空题6.(2014秋 昆明校级期末)将一副三角板如图摆放,若∠BAE=135°17′,则∠CAD的度数是____. ( http: / / www.21cnjy.com )7.(2013秋 吴江市期末)如图,将三个同样的正方形的一个顶点重合放置,那么∠1的度数为______. ( http: / / www.21cnjy.com )三、解答题8.如图,∠1=∠2=∠3=∠4,根据图形回答:(1)图中哪些角是∠2的2倍?(2)图中哪些角是∠3的3倍?(3)图中哪些角是∠AOD的?(4)射线OC是哪个角的三等分线? ( http: / / www.21cnjy.com )9.(2014秋 阜宁县期末)如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.(1)若∠AOC=50°,求出∠BOD的度数;(2)试判断OE是否平分∠BOC,并说明理由. ( http: / / www.21cnjy.com )10.(2013秋 定州市期末) 如图所示,点A、O、B在同一直线上,OC平分∠AOB,若∠COD=30°.(1)求∠BOD的度数;(2)如果∠AOE=150°,请你通过计算判断:OE是∠BOD的平分线吗? ( http: / / www.21cnjy.com )11.(2014秋 宁化县校级期中)如图,已知∠AOB=∠COD=90°,OC平分∠AOB,OE是∠BOD的三等分线,求∠COE的度数. ( http: / / www.21cnjy.com )12.(2014 郸城县校级模拟)已知,OM、ON分别是∠AOC,∠BOC的角平分线. ( http: / / www.21cnjy.com )(1)如图1,若∠AOB=120°,∠BOC=30°,则∠MON=_______.(2)如图1,若∠AOB=120°,∠BOC=β°,能否求出∠MON的度数?若能,求出其值,若不能,试说明理由;(3)如图2,若∠AOB=α°,∠BOC=β ( http: / / www.21cnjy.com )°,是否仍然能求出∠MON的度数,若能,求∠MON的度数(用含α或β的式子表示),并从你的求解过程中总结出你发现的规律.13.(2014春 江阴市 ( http: / / www.21cnjy.com )期末)如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.(1)将图1中的三角板绕点O顺时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠CON的度数;(2)将图1中的三角板绕 ( http: / / www.21cnjy.com )点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为秒(直接写出结果);(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究∠AOM与∠NOC之间的数量关系,并说明理由. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】因为285°角是15° ( http: / / www.21cnjy.com )的19倍,所以能用一副三角板画出285°的角.具体画法不唯一,如:先连续画7次45°,得到315°角,再减去30°,可得所要求作的285°角,即7×45°-30°=285°.
练1 【解析】∠ABC等于30度角与直角的和,据此即可计算得到.
解:∠ABC=30°+90°=120°.
故选D.
【例2】【解析】此题要根据题意列出代数式.可先根据∠MON与∠BOC的关系求出∠CON与∠BOM,再根据角平分线的知识求出∠AOD.
解:∵∠MON=α,∠BOC=β
∴∠MON﹣∠BOC=∠CON+∠BOM=α﹣β
又∵OM平分∠AOB,ON平分∠COD
∴∠CON=∠DON,∠AOM=∠BOM
由题意得∠AOD=∠MON+∠DON+∠AOM=∠MON+∠CON+∠BOM=α+(α﹣β)=2α﹣β.
故选A.
练2 【解析】根据四边形ABCD是矩形,得出∠ABE=∠EBD=∠ABD,∠DBF=∠FBC=∠DBC,再根据∠ABE+∠EBD+∠DBF+∠FBC=∠ABC=90°,得出∠EBD+∠DBF=45°,从而求出答案.
解:∵四边形ABCD是矩形,
根据折叠可得∠ABE=∠EBD=∠ABD,∠DBF=∠FBC=∠DBC,
∵∠ABE+∠EBD+∠DBF+∠FBC=∠ABC=90°,
∴∠EBD+∠DBF=45°,
即∠EBF=45°,
故答案为:45°.
点评:此题考查了角的计算和翻折变换,解题的关键是找准图形翻折后,哪些角是相等的,再进行计算,是一道基础题.
【例3】【解析】分类讨论:当∠AOC=∠AOB或∠AOC=∠AOB,然后把∠AOB=45°代入计算即可.
解:当∠AOC=∠AOB时,则∠AOC=×45°=15°,
当∠AOC=∠AOB时,则∠AOC=×45°=30°,
则∠AOC的度数是15°或30°;
故选C.
点评:本题考查了角的计算:要根据射线OC的位置不同,分类讨论,分别求出∠AOC的度数.
练3 【解析】∵OE⊥OA,∴∠AOB+∠BOE=90°,
∵∠BOE=75°,∴∠AOB=15°.
∵OB、OC是∠AOD的三等分线,
∴∠AOD=3∠AOB=45°,
∴∠DOE=90°﹣∠AOD=45°.
故答案为:45°
点评:本题考查了垂直、等分角的定义.
课后小测答案:
一、选择题
1.【解析】先根据OB是∠AOC的角平 ( http: / / www.21cnjy.com )分线,OD是∠COE的角平分线,∠AOB=40°,∠COE=60°求出∠BOC与∠COD的度数,再根据∠BOD=∠BOC+∠COD即可得出结论.
解:∵OB是∠AOC的角平分线,OD是∠COE的角平分线,∠AOB=40°,∠COE=60°,
∴∠BOC=∠AOB=40°,∠COD=∠COE=×60°=30°,
∴∠BOD=∠BOC+∠COD=40°+30°=70°.
故选:D.
2.【解析】利用直角三角板的知识和角的和差关系计算.
解:因为是直角三角板,所以∠BAC=∠DAE=90°,
所以∠BAD+∠DAC+∠CAE+∠DAC=180°,
即∠BAE+∠DAC=180°.
故选C.
点评:本题是有公共部分的直角计算问题,关键是不要漏掉公共部分.
3.【解析】利用直角和角的组成即角的和差关系计算.
解:∵三角板的两个直角都等于90°,所以∠BOD+∠AOC=180°,
∵∠BOD+∠AOC=∠AOB+∠COD,
∵∠AOB=155°,
∴∠COD等于25°.
故选B.
4.【解析】一副三角板各角的度数是30度,60度,45度,90度,因而把他们相加减就可以拼出的度数,据此得出选项.
解:已知一副三角板各角的度数是30度,60度,45度,90度,
可以拼出的度数就是用30度,60度,45度,90度相加减,
45°+60°=105°,
30°+45°=75°,
45°﹣30°=15°,
显然得不到85°.
故选:C.
5.【解析】分类讨论:当∠AOC=∠AOB或∠AOC=∠AOB,然后把∠AOB=60°代入计算即可.
解:当∠AOC=∠AOB,则∠AOC=×60°=20°;
当∠AOC=∠AOB,则∠AOC=×60°=40°.
故选C.
二、填空题
6.【解析】利用三角形的各角度数和图中角与角的关系计算.
解:∠BAE=∠BAD+∠CAE﹣∠CAD
则∠CAD=∠BAD+∠CAE﹣∠BAE=90+90﹣∠BAE=44°43′.
故填44°43′.
点评:对∠BAE=∠BAD+∠CAE﹣∠CAD这一关系的认识是解题的关键.
7.【解析】根据∠1=∠BOD+EOC﹣∠BOE,利用正方形的角都是直角,即可求得∠BOD和∠EOC的度数从而求解.
解:∵∠BOD=90°﹣∠AOB=90°﹣30°=60°
∠EOC=90°﹣∠EOF=90°﹣40°=50°
又∵∠1=∠BOD+EOC﹣∠BOE
∴∠1=60°+50°﹣90°=20°
故答案是:20°.
( http: / / www.21cnjy.com )
点评:本题主要考查了角度的计算,正确理解∠1=∠BOD+EOC﹣∠BOE这一关系是解决本题的关键.
三、解答题
8.【解析】(1)根据∠1=∠2=∠3=∠4,找出是∠2的2倍的角可以解题;
(2)根据∠1=∠2=∠3=∠4,找出是∠3的3倍的角可以解题;
(3)根据∠1=∠2=∠3=∠4,找出图中哪些角是∠AOD的即可解题;
(3)根据∠1=∠2=∠3=∠4,找出射线OC是哪个角的三等分线即可解题.
解:(1)∵∠ACD=∠1+∠2,∠CDE=∠2+∠3,∠BOD=∠3+∠4,∠1=∠2=∠3=∠4
∴∠ACD,∠CDE,∠BOD是∠2的2倍;
(2)∠BOC=∠3+∠4+∠2,∠AOE=∠1+∠2+∠3,∠1=∠2=∠3=∠4
∴∠BOC,∠AOE是∠3的3倍;
(3)∵∠AOD=∠1+∠2,∠1=∠2
∴∠AOD=∠1,
∴∠1、∠2、∠3、∠4均为∠AOD的.
(4)∵∠1=∠2=∠3,
∴OC是∠AOE的三等分线.
9.【解析】(1)根据∠BOD=∠DOC+∠BOC,首先利用角平分线的定义和邻补角的定义求得∠DOC和∠BOC即可;
(2)根据∠COE=∠DOE﹣∠DOC和∠BOE=∠BOD﹣∠DOE分别求得∠COE与∠BOE的度数即可说明.
解:(1)因为∠AOC=50°,OD平分∠AOC,
所以∠DOC=∠AOC=25°,∠BOC=180°﹣∠AOC=130°,
所以∠BOD=∠DOC+∠BOC=155°;
(2)OE平分∠BOC.理由如下:
因为∠DOE=90°,∠DOC=25°,
所以∠COE=∠DOE﹣∠DOC=90°﹣25°=65°.
又因为∠BOE=∠BOD﹣∠DOE=155°﹣90°=65°,
所以∠COE=∠BOE,
所以OE平分∠BOC.
点评:本题主要考查了角的度数的计算,正确理解角平分线的定义,以及邻补角的定义是解题的关键.
10.【解析】(1)根据角平分线分角相等,可得∠BOC=∠AOC=90°,再根据角的和差,可得答案;
(2)根据射线所分的角相等,可得射线是角平分线.
解:(1)因为A、O、B在同一直线上
所以∠AOB=180°
因为OC平分∠AOB
所以∠AOC=∠BOC=90°
因为∠COD=30°
所以∠BOD=∠BOC﹣∠COD
=90°﹣30°=60°;
(2)因为∠AOE=150°,∠AOB=180°
所以∠BOE=180°﹣150°=30°
因为∠BOD=60°
所以∠DOE=∠BOD﹣∠BOE=60°﹣30°=30°
所以∠BOE=∠DOE
所以OE∠BOD的平分线.
点评:本题考查了角平分线,角平分线所分角相等,分角相等的射线是角平分线.
11.【解析】先根据∠AOB=∠C ( http: / / www.21cnjy.com )OD=90°,OC平分∠AOB求出∠AOC=∠BOC=45°,故可得出∠BOD=45°,再由OE是∠BOD的三等分线得出∠BOE的度数,根据∠COE=∠BOC+∠BOE即可得出结论.
解:∵∠AOB=∠COD=90°,OC平分∠AOB,
∠AOC=∠BOC=45°,
∴∠BOD=45°.
∵OE是∠BOD的三等分线,
∴∠BOE=∠BOD=×45°=30°,
∴∠COE=∠BOC+∠BOE=45°+30°=75°.
点评:本题考查的是角平分线的定义,熟知从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线是解答此题的关键.
12.【解析】(1)根据∠AOB=120 ( http: / / www.21cnjy.com )°,∠BOC=30°,可得∠AOC=∠AOB+∠BOC=120°+30°=150°,再利用OM是∠AOC的平分线,ON是∠BOC的平分线,即可求得答案;
(2)根据∠MON=∠MOC﹣∠NOC,又利用∠AOB=120°,∠BOC=β°,由(1)可得出答案;
(3)利用(1)(2)的计算方法得出规律即可.
解:(1)∵∠AOB=120°,∠BOC=30°,
∴∠AOC=∠AOB+∠BOC=120°+30°=150°,
∵OM是∠AOC的平分线,ON是∠BOC的平分线,
∴∠MOC=∠AOC,∠NOC=∠BOC,
∴∠MON=∠MOC﹣∠NOC=75°﹣15°=60°,
(2)当∠AOB=120°,∠BOC=β°时,
∴∠MON=∠MOC﹣∠NOC=(120+β)°﹣=60°;
(3)由(1)(2)可知:
∴∠MON=∠MOC﹣∠NOC=(α+β)°﹣=.
∠MON的度数始终等于∠AOB角度的一半.
点评:此题主要考查角的计算和角平分线的定义等知识点的理解和掌握,难度不大,属于基础题.
13.【解析】(1)由角的平分线的定义和等角的余角相等求解;
(2)由∠BOC=120°可得∠AO ( http: / / www.21cnjy.com )C=60°,则∠AON=30°或∠NOR=30°,即顺时针旋转300°或120°时ON平分∠AOC,据此求解;
(3)因为∠MON=90°,∠AOC=60°,所以∠AOM=90°﹣∠AON、∠NOC=60°﹣∠AON,然后作差即可.
解:(1)已知∠AOC=60°,
∴∠BOC=120°,
又OM平分∠BOC,
∠COM=∠BOC=60°,
∴∠CON=∠COM+90°=150°;
(2)延长NO,
∵∠BOC=120°
∴∠AOC=60°,
当直线ON恰好平分锐角∠AOC,
∴∠AOD=∠COD=30°,
即顺时针旋转300°时NO延长线平分∠AOC,
由题意得,10t=300°
∴t=30,
当NO平分∠AOC,
∴∠NOR=30°,
即顺时针旋转120°时NO平分∠AOC,
∴10t=120°,
∴t=12,
∴t=12或30;
(3)∵∠MON=90°,∠AOC=60°,
∴∠AOM=90°﹣∠AON、∠NOC=60°﹣∠AON,
∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°,
所以∠AOM与∠NOC之间的数量关系为:∠AOM﹣∠NOC=30°.
( http: / / www.21cnjy.com )
点评:此题考查了角的计算,关键是应该认真审题并仔细观察图形,找到各个量之间的关系,是解题的关键.
二、知识回顾 1. 三角板的认识一副三角板的各个角分别是多少度? 30°、60°、90°;45°、45°、90° 2. 角的平分线从一个角的 顶点 出发,把这个角分成 ( http: / / www.21cnjy.com ) 大小相等 的两个角的射线,叫做这个角的平分线.类似地,还有角的三等分线等.如下图中的OB、OC是∠AOD的三等分线. ( http: / / www.21cnjy.com )
三、新知讲解 三角板中的计算问题如图,一副三角板共 ( http: / / www.21cnjy.com )有6个角,且有30°,4 ( http: / / www.21cnjy.com )5°,60°,90°四种角度,如果只用一副三角板,你能作出哪些不同大小的角?看起来这个问题似乎很简单,但是,若仔细地思考一番,想要找到问题的答案,也并非容易. ( http: / / www.21cnjy.com )尝试1:只用一个三角板画用1个三角板可以画出30°,45°,60°,90°,180°这几个特殊角.尝试2:利用两个三角板中的特殊角的和画用2个三角板的两个角,并将角叠加,就可以得 ( http: / / www.21cnjy.com )到75°,105°,120°,150°等特殊角.如图2,将30°角与45°角拼在一起可以画出75°的角,即∠AOB.如图3,将60°角与45°角拼在一起,可以画出105°的角,即∠AOB. ( http: / / www.21cnjy.com )图2 图3尝试3:利用两个三角板中的特殊角的差画应用三角板先画一些特殊角, ( http: / / www.21cnjy.com )再减去一些特殊角,就可以得到15°,120°,135°,150°等特殊角.如图4,利用45°和30°的角.就可以画出15°的角,即∠BOC.如图5,利用180°和30°的角,可以画出150°的角. ( http: / / www.21cnjy.com )图4 图5通过尝试发现:只要是15°的倍数的角,都可以用一副三角板画出来.但应注意同一个角度有多种不同的画法,如120°的角既可以用30°与90°的和画出来,也可以用180°与60°的差画出来.
四、典例探究 扫一扫,有惊喜哦!1.三角板中的计算问题【例1】如果不考虑用90°和60°角,你能用一副三角板拼画出285°的角吗?总结:只要是15°的倍数的角,都可以用一副三角板画出来.具体画法不唯一.练1把两块三角板按如图所示那样拼在一起,则∠ABC等于( ) ( http: / / www.21cnjy.com )A.70° B.90° C.105° D.120°2.几何图形中的角度计算【例2】如图所示,OB,OC是∠A ( http: / / www.21cnjy.com )OD的任意两条射线,OM平分∠AOB,ON平分∠COD,若∠MON=α,∠BOC=β,则表示∠AOD等于( ) ( http: / / www.21cnjy.com )A.2α﹣β B.α﹣β C.α+β D.2α+β总结:如下图,已知 OM平分∠AO ( http: / / www.21cnjy.com )B,ON平分∠COD,则∠BOC,∠MON,∠AOD之间存在着一个等量关系,即:∠BOC+∠AOD =2∠MON.练2如图,将矩形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF=_____. ( http: / / www.21cnjy.com )3.角n等分线的综合计算【例3】已知∠AOB=45°,OC是∠AOB的一条三等分线,则∠AOC的度数是( )A.15° B.30° C.15°或30° D.不能确定总结:注意一个角的三等分线有两条,当题中没有明确是哪一条,也没有给出图形的话,需要分类讨论.练3如图,OE⊥OA,OB、OC是∠AOD的三等分线,∠BOE=75°,则∠DOE=________. ( http: / / www.21cnjy.com )
五、课后小测 一、选择题1.如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为( ) ( http: / / www.21cnjy.com )A.50° B.60° C.65° D.70°2.(2013秋 晋江市期末)将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),下列结论一定成立的是( ) ( http: / / www.21cnjy.com )A.∠BAE>∠DAC B.∠BAE﹣∠DAC=45°C.∠BAE+∠DAC=180° D.∠BAD≠∠EAC3.(2014秋 汉阳区期末)如图,小明将自己用的一副三角板摆成如图形状,如果∠AOB=155°,那么∠COD等于( ) ( http: / / www.21cnjy.com )A.15° B.25° C.35° D.45°4.(2014秋 贵阳校级期末)用一副三角板不可以拼出的角是( )A.105° B.75° C.85° D.15°5.(2011秋 和平区期末)已知射线OC是∠AOB的一条三等分线,若∠AOB=60°,则∠AOC为( )A.20° B.40° C.20°或40° D.15°或20°二、填空题6.(2014秋 昆明校级期末)将一副三角板如图摆放,若∠BAE=135°17′,则∠CAD的度数是____. ( http: / / www.21cnjy.com )7.(2013秋 吴江市期末)如图,将三个同样的正方形的一个顶点重合放置,那么∠1的度数为______. ( http: / / www.21cnjy.com )三、解答题8.如图,∠1=∠2=∠3=∠4,根据图形回答:(1)图中哪些角是∠2的2倍?(2)图中哪些角是∠3的3倍?(3)图中哪些角是∠AOD的?(4)射线OC是哪个角的三等分线? ( http: / / www.21cnjy.com )9.(2014秋 阜宁县期末)如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.(1)若∠AOC=50°,求出∠BOD的度数;(2)试判断OE是否平分∠BOC,并说明理由. ( http: / / www.21cnjy.com )10.(2013秋 定州市期末) 如图所示,点A、O、B在同一直线上,OC平分∠AOB,若∠COD=30°.(1)求∠BOD的度数;(2)如果∠AOE=150°,请你通过计算判断:OE是∠BOD的平分线吗? ( http: / / www.21cnjy.com )11.(2014秋 宁化县校级期中)如图,已知∠AOB=∠COD=90°,OC平分∠AOB,OE是∠BOD的三等分线,求∠COE的度数. ( http: / / www.21cnjy.com )12.(2014 郸城县校级模拟)已知,OM、ON分别是∠AOC,∠BOC的角平分线. ( http: / / www.21cnjy.com )(1)如图1,若∠AOB=120°,∠BOC=30°,则∠MON=_______.(2)如图1,若∠AOB=120°,∠BOC=β°,能否求出∠MON的度数?若能,求出其值,若不能,试说明理由;(3)如图2,若∠AOB=α°,∠BOC=β ( http: / / www.21cnjy.com )°,是否仍然能求出∠MON的度数,若能,求∠MON的度数(用含α或β的式子表示),并从你的求解过程中总结出你发现的规律.13.(2014春 江阴市 ( http: / / www.21cnjy.com )期末)如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.(1)将图1中的三角板绕点O顺时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠CON的度数;(2)将图1中的三角板绕 ( http: / / www.21cnjy.com )点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为秒(直接写出结果);(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究∠AOM与∠NOC之间的数量关系,并说明理由. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】因为285°角是15° ( http: / / www.21cnjy.com )的19倍,所以能用一副三角板画出285°的角.具体画法不唯一,如:先连续画7次45°,得到315°角,再减去30°,可得所要求作的285°角,即7×45°-30°=285°.
练1 【解析】∠ABC等于30度角与直角的和,据此即可计算得到.
解:∠ABC=30°+90°=120°.
故选D.
【例2】【解析】此题要根据题意列出代数式.可先根据∠MON与∠BOC的关系求出∠CON与∠BOM,再根据角平分线的知识求出∠AOD.
解:∵∠MON=α,∠BOC=β
∴∠MON﹣∠BOC=∠CON+∠BOM=α﹣β
又∵OM平分∠AOB,ON平分∠COD
∴∠CON=∠DON,∠AOM=∠BOM
由题意得∠AOD=∠MON+∠DON+∠AOM=∠MON+∠CON+∠BOM=α+(α﹣β)=2α﹣β.
故选A.
练2 【解析】根据四边形ABCD是矩形,得出∠ABE=∠EBD=∠ABD,∠DBF=∠FBC=∠DBC,再根据∠ABE+∠EBD+∠DBF+∠FBC=∠ABC=90°,得出∠EBD+∠DBF=45°,从而求出答案.
解:∵四边形ABCD是矩形,
根据折叠可得∠ABE=∠EBD=∠ABD,∠DBF=∠FBC=∠DBC,
∵∠ABE+∠EBD+∠DBF+∠FBC=∠ABC=90°,
∴∠EBD+∠DBF=45°,
即∠EBF=45°,
故答案为:45°.
点评:此题考查了角的计算和翻折变换,解题的关键是找准图形翻折后,哪些角是相等的,再进行计算,是一道基础题.
【例3】【解析】分类讨论:当∠AOC=∠AOB或∠AOC=∠AOB,然后把∠AOB=45°代入计算即可.
解:当∠AOC=∠AOB时,则∠AOC=×45°=15°,
当∠AOC=∠AOB时,则∠AOC=×45°=30°,
则∠AOC的度数是15°或30°;
故选C.
点评:本题考查了角的计算:要根据射线OC的位置不同,分类讨论,分别求出∠AOC的度数.
练3 【解析】∵OE⊥OA,∴∠AOB+∠BOE=90°,
∵∠BOE=75°,∴∠AOB=15°.
∵OB、OC是∠AOD的三等分线,
∴∠AOD=3∠AOB=45°,
∴∠DOE=90°﹣∠AOD=45°.
故答案为:45°
点评:本题考查了垂直、等分角的定义.
课后小测答案:
一、选择题
1.【解析】先根据OB是∠AOC的角平 ( http: / / www.21cnjy.com )分线,OD是∠COE的角平分线,∠AOB=40°,∠COE=60°求出∠BOC与∠COD的度数,再根据∠BOD=∠BOC+∠COD即可得出结论.
解:∵OB是∠AOC的角平分线,OD是∠COE的角平分线,∠AOB=40°,∠COE=60°,
∴∠BOC=∠AOB=40°,∠COD=∠COE=×60°=30°,
∴∠BOD=∠BOC+∠COD=40°+30°=70°.
故选:D.
2.【解析】利用直角三角板的知识和角的和差关系计算.
解:因为是直角三角板,所以∠BAC=∠DAE=90°,
所以∠BAD+∠DAC+∠CAE+∠DAC=180°,
即∠BAE+∠DAC=180°.
故选C.
点评:本题是有公共部分的直角计算问题,关键是不要漏掉公共部分.
3.【解析】利用直角和角的组成即角的和差关系计算.
解:∵三角板的两个直角都等于90°,所以∠BOD+∠AOC=180°,
∵∠BOD+∠AOC=∠AOB+∠COD,
∵∠AOB=155°,
∴∠COD等于25°.
故选B.
4.【解析】一副三角板各角的度数是30度,60度,45度,90度,因而把他们相加减就可以拼出的度数,据此得出选项.
解:已知一副三角板各角的度数是30度,60度,45度,90度,
可以拼出的度数就是用30度,60度,45度,90度相加减,
45°+60°=105°,
30°+45°=75°,
45°﹣30°=15°,
显然得不到85°.
故选:C.
5.【解析】分类讨论:当∠AOC=∠AOB或∠AOC=∠AOB,然后把∠AOB=60°代入计算即可.
解:当∠AOC=∠AOB,则∠AOC=×60°=20°;
当∠AOC=∠AOB,则∠AOC=×60°=40°.
故选C.
二、填空题
6.【解析】利用三角形的各角度数和图中角与角的关系计算.
解:∠BAE=∠BAD+∠CAE﹣∠CAD
则∠CAD=∠BAD+∠CAE﹣∠BAE=90+90﹣∠BAE=44°43′.
故填44°43′.
点评:对∠BAE=∠BAD+∠CAE﹣∠CAD这一关系的认识是解题的关键.
7.【解析】根据∠1=∠BOD+EOC﹣∠BOE,利用正方形的角都是直角,即可求得∠BOD和∠EOC的度数从而求解.
解:∵∠BOD=90°﹣∠AOB=90°﹣30°=60°
∠EOC=90°﹣∠EOF=90°﹣40°=50°
又∵∠1=∠BOD+EOC﹣∠BOE
∴∠1=60°+50°﹣90°=20°
故答案是:20°.
( http: / / www.21cnjy.com )
点评:本题主要考查了角度的计算,正确理解∠1=∠BOD+EOC﹣∠BOE这一关系是解决本题的关键.
三、解答题
8.【解析】(1)根据∠1=∠2=∠3=∠4,找出是∠2的2倍的角可以解题;
(2)根据∠1=∠2=∠3=∠4,找出是∠3的3倍的角可以解题;
(3)根据∠1=∠2=∠3=∠4,找出图中哪些角是∠AOD的即可解题;
(3)根据∠1=∠2=∠3=∠4,找出射线OC是哪个角的三等分线即可解题.
解:(1)∵∠ACD=∠1+∠2,∠CDE=∠2+∠3,∠BOD=∠3+∠4,∠1=∠2=∠3=∠4
∴∠ACD,∠CDE,∠BOD是∠2的2倍;
(2)∠BOC=∠3+∠4+∠2,∠AOE=∠1+∠2+∠3,∠1=∠2=∠3=∠4
∴∠BOC,∠AOE是∠3的3倍;
(3)∵∠AOD=∠1+∠2,∠1=∠2
∴∠AOD=∠1,
∴∠1、∠2、∠3、∠4均为∠AOD的.
(4)∵∠1=∠2=∠3,
∴OC是∠AOE的三等分线.
9.【解析】(1)根据∠BOD=∠DOC+∠BOC,首先利用角平分线的定义和邻补角的定义求得∠DOC和∠BOC即可;
(2)根据∠COE=∠DOE﹣∠DOC和∠BOE=∠BOD﹣∠DOE分别求得∠COE与∠BOE的度数即可说明.
解:(1)因为∠AOC=50°,OD平分∠AOC,
所以∠DOC=∠AOC=25°,∠BOC=180°﹣∠AOC=130°,
所以∠BOD=∠DOC+∠BOC=155°;
(2)OE平分∠BOC.理由如下:
因为∠DOE=90°,∠DOC=25°,
所以∠COE=∠DOE﹣∠DOC=90°﹣25°=65°.
又因为∠BOE=∠BOD﹣∠DOE=155°﹣90°=65°,
所以∠COE=∠BOE,
所以OE平分∠BOC.
点评:本题主要考查了角的度数的计算,正确理解角平分线的定义,以及邻补角的定义是解题的关键.
10.【解析】(1)根据角平分线分角相等,可得∠BOC=∠AOC=90°,再根据角的和差,可得答案;
(2)根据射线所分的角相等,可得射线是角平分线.
解:(1)因为A、O、B在同一直线上
所以∠AOB=180°
因为OC平分∠AOB
所以∠AOC=∠BOC=90°
因为∠COD=30°
所以∠BOD=∠BOC﹣∠COD
=90°﹣30°=60°;
(2)因为∠AOE=150°,∠AOB=180°
所以∠BOE=180°﹣150°=30°
因为∠BOD=60°
所以∠DOE=∠BOD﹣∠BOE=60°﹣30°=30°
所以∠BOE=∠DOE
所以OE∠BOD的平分线.
点评:本题考查了角平分线,角平分线所分角相等,分角相等的射线是角平分线.
11.【解析】先根据∠AOB=∠C ( http: / / www.21cnjy.com )OD=90°,OC平分∠AOB求出∠AOC=∠BOC=45°,故可得出∠BOD=45°,再由OE是∠BOD的三等分线得出∠BOE的度数,根据∠COE=∠BOC+∠BOE即可得出结论.
解:∵∠AOB=∠COD=90°,OC平分∠AOB,
∠AOC=∠BOC=45°,
∴∠BOD=45°.
∵OE是∠BOD的三等分线,
∴∠BOE=∠BOD=×45°=30°,
∴∠COE=∠BOC+∠BOE=45°+30°=75°.
点评:本题考查的是角平分线的定义,熟知从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线是解答此题的关键.
12.【解析】(1)根据∠AOB=120 ( http: / / www.21cnjy.com )°,∠BOC=30°,可得∠AOC=∠AOB+∠BOC=120°+30°=150°,再利用OM是∠AOC的平分线,ON是∠BOC的平分线,即可求得答案;
(2)根据∠MON=∠MOC﹣∠NOC,又利用∠AOB=120°,∠BOC=β°,由(1)可得出答案;
(3)利用(1)(2)的计算方法得出规律即可.
解:(1)∵∠AOB=120°,∠BOC=30°,
∴∠AOC=∠AOB+∠BOC=120°+30°=150°,
∵OM是∠AOC的平分线,ON是∠BOC的平分线,
∴∠MOC=∠AOC,∠NOC=∠BOC,
∴∠MON=∠MOC﹣∠NOC=75°﹣15°=60°,
(2)当∠AOB=120°,∠BOC=β°时,
∴∠MON=∠MOC﹣∠NOC=(120+β)°﹣=60°;
(3)由(1)(2)可知:
∴∠MON=∠MOC﹣∠NOC=(α+β)°﹣=.
∠MON的度数始终等于∠AOB角度的一半.
点评:此题主要考查角的计算和角平分线的定义等知识点的理解和掌握,难度不大,属于基础题.
13.【解析】(1)由角的平分线的定义和等角的余角相等求解;
(2)由∠BOC=120°可得∠AO ( http: / / www.21cnjy.com )C=60°,则∠AON=30°或∠NOR=30°,即顺时针旋转300°或120°时ON平分∠AOC,据此求解;
(3)因为∠MON=90°,∠AOC=60°,所以∠AOM=90°﹣∠AON、∠NOC=60°﹣∠AON,然后作差即可.
解:(1)已知∠AOC=60°,
∴∠BOC=120°,
又OM平分∠BOC,
∠COM=∠BOC=60°,
∴∠CON=∠COM+90°=150°;
(2)延长NO,
∵∠BOC=120°
∴∠AOC=60°,
当直线ON恰好平分锐角∠AOC,
∴∠AOD=∠COD=30°,
即顺时针旋转300°时NO延长线平分∠AOC,
由题意得,10t=300°
∴t=30,
当NO平分∠AOC,
∴∠NOR=30°,
即顺时针旋转120°时NO平分∠AOC,
∴10t=120°,
∴t=12,
∴t=12或30;
(3)∵∠MON=90°,∠AOC=60°,
∴∠AOM=90°﹣∠AON、∠NOC=60°﹣∠AON,
∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°,
所以∠AOM与∠NOC之间的数量关系为:∠AOM﹣∠NOC=30°.
( http: / / www.21cnjy.com )
点评:此题考查了角的计算,关键是应该认真审题并仔细观察图形,找到各个量之间的关系,是解题的关键.
