数学人教A版(2019)必修第二册9.2.3总体集中趋势的估计 课件(共22张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册9.2.3总体集中趋势的估计 课件(共22张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-09 23:41:22 | ||
图片预览





文档简介
(共22张PPT)
9.2.3 总体集中趋势的估计
第九章 统 计
9.2 用样本估计总体
新课导入
为了了解总体的情况,前面我们研究了如何通过样本的分布规律估计总体的分布规律.但有时候,我们可能不太关心总体的分布规律,而更关注总体取值在某一方面的特征.
例如,对于某县今年小麦的收成情况,我们可能会更关注该县今年小麦的总产量或平均每公顷的产量,而不是产量的分布;对于一个国家国民的身高情况,我们可能会更关注身高的平均数或中位数,而不是身高的分布;等等.
在初中的学习中我们已经了解到,平均数、中位数和众数等都是刻画“中心位置”的量,它们从不同角度刻画了一组数据的集中趋势. 那你是否还记得平均数、中位数、众数是什么吗?这些统计量刻画了数据的什么特点?
众数:
中位数:
当数据个数是奇数时,处在最中间的数是中位数;
当数据个数是偶数时,最中间两个数的平均数是中位数.
(第50百分位数)
平均数:
平均数、中位数、众数的定义
复习回顾
一组数据中出现次数最多的数.
一组数据按从小到大排序,
注意单位(t)
下面我们通过具体实例进一步了解这些量的意义,探究它们之间的联系与区别,并根据样本的集中趋势估计总体的集中趋势.
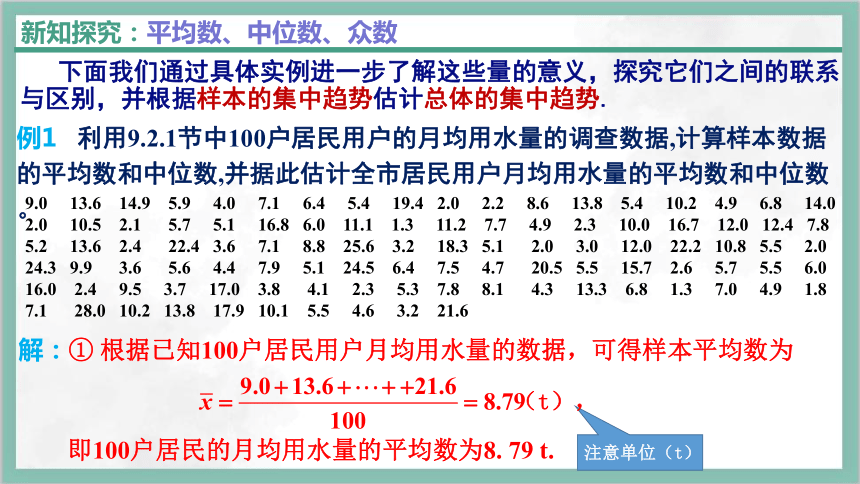
例1 利用9.2.1节中100户居民用户的月均用水量的调查数据,计算样本数据的平均数和中位数,并据此估计全市居民用户月均用水量的平均数和中位数。
9.0 13.6 14.9 5.9 4.0 7.1 6.4 5.4 19.4 2.0 2.2 8.6 13.8 5.4 10.2 4.9 6.8 14.0 2.0 10.5 2.1 5.7 5.1 16.8 6.0 11.1 1.3 11.2 7.7 4.9 2.3 10.0 16.7 12.0 12.4 7.8 5.2 13.6 2.4 22.4 3.6 7.1 8.8 25.6 3.2 18.3 5.1 2.0 3.0 12.0 22.2 10.8 5.5 2.0 24.3 9.9 3.6 5.6 4.4 7.9 5.1 24.5 6.4 7.5 4.7 20.5 5.5 15.7 2.6 5.7 5.5 6.0 16.0 2.4 9.5 3.7 17.0 3.8 4.1 2.3 5.3 7.8 8.1 4.3 13.3 6.8 1.3 7.0 4.9 1.8 7.1 28.0 10.2 13.8 17.9 10.1 5.5 4.6 3.2 21.6
解:① 根据已知100户居民用户月均用水量的数据,可得样本平均数为
即100户居民的月均用水量的平均数为8. 79 t.
新知探究:平均数、中位数、众数
新知探究:平均数、中位数、众数
解:
②将样本数据按从小到大排序,结果如下:
1.3 1.3 1.8 2.0 2.0 2.0 2.0 2.1 2.2 2.3 2.3 2.4 2.4 2.6 3.0 3.2 3.2 3.6 3.6 3.7 3.8 4.0 4.1 4.3 4.4 4.6 4.7 4.9 4.9 4.9 5.1 5.1 5.1 5.2 5.3 5.4 5.4 5.5 5.5 5.5 5.5 5.6 5.7 5.7 5.9 6.0 6.0 6.4 6.4 6.8 6.8 7.0 7.1 7.1 7.1 7.5 7.7 7.8 7.8 7.9 8.1 8.6 8.8 9.0 9.5 9.9 10.0 10.1 10.2 10.2 10.5 10.8 11.1 11.2 12.0 12.0 12.4 13.3 13.6 13.6 13.8 13.8 14.0 14.9 15.7 16.0 16.7 16.8 17.0 17.9 18.3 19.4 20.5 21.6 22.2 22.4 24.3 24.5 25.6 28.0
6.8 6.8
由上述数据可得,第50个数和第51个数均为6.8,由中位数的定义,可得,100户居民的月均用水量的中位数是6.8t.
因为数据是抽自全市居民户的简单随机样本,所以我们可以据此估计全市居民用户的月均用水量约为8.79 t,其中位数约为6.8 t,众数是2.0和5.5t.
问题1 设某个居民小区有2000户,你能估计该小区的月用水总量吗?
③由众数的定义,可得100户居民的月均用水量的众数是
2.0和5.5 t.
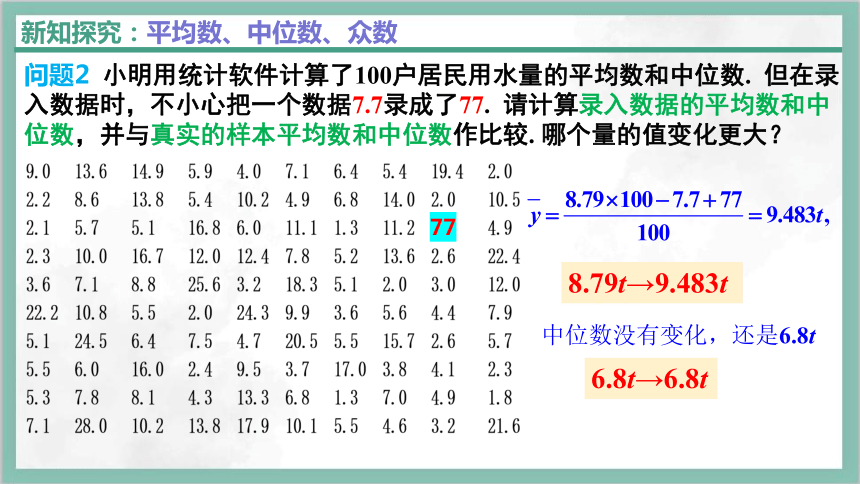
问题2 小明用统计软件计算了100户居民用水量的平均数和中位数. 但在录入数据时,不小心把一个数据7.7录成了77. 请计算录入数据的平均数和中位数,并与真实的样本平均数和中位数作比较. 哪个量的值变化更大?
新知探究:平均数、中位数、众数
77
8.79t→9.483t
6.8t→6.8t
新知探究:平均数、中位数、众数
问题3 你能解释出现问题2中现象的原因吗?
中位数
平均数
(1)平均数有所变化;样本的平均数与每个数据有关,样本中的每一个数据的变化都能引起平均数的变化;
(2)中位数只与样本数据中间位置的一个或两个值有关,与其他数据无关,所以不是任何一个样本数据的改变都会引起中位数的改变.
与中位数比较,平均数反映出样本数据中的更多信息,对样本中的极端值更加敏感。
8.79t→9.483t
6.8t→6.8t
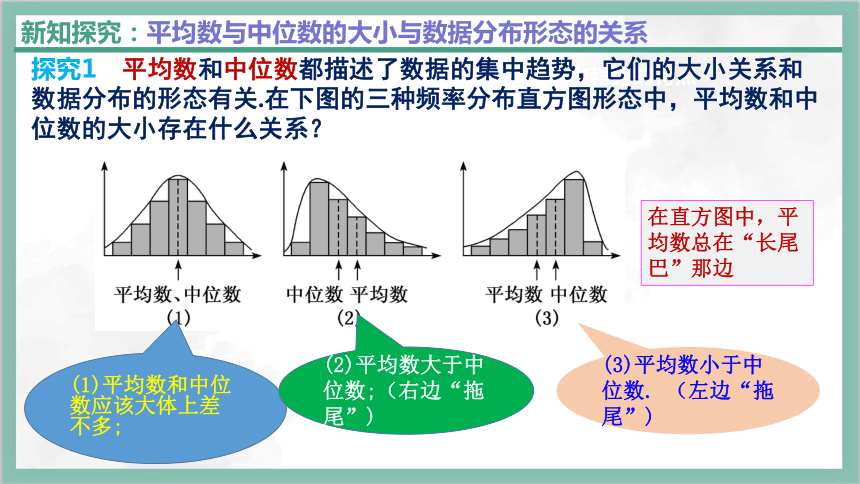
(1)平均数和中位数应该大体上差不多;
(2)平均数大于中位数;(右边“拖尾”)
(3)平均数小于中位数. (左边“拖尾”)
在直方图中,平均数总在“长尾巴”那边
平均数、中位数、众数刻画一组数据的集中趋势的特点
探究1 平均数和中位数都描述了数据的集中趋势,它们的大小关系和数据分布的形态有关.在下图的三种频率分布直方图形态中,平均数和中位数的大小存在什么关系?
新知探究:平均数与中位数的大小与数据分布形态的关系
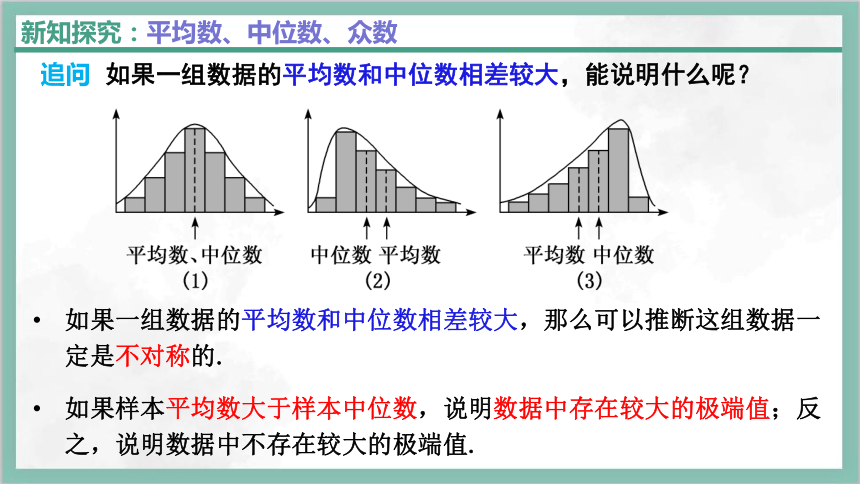
追问 如果一组数据的平均数和中位数相差较大,能说明什么呢?
新知探究:平均数、中位数、众数
如果一组数据的平均数和中位数相差较大,那么可以推断这组数据一定是不对称的.
如果样本平均数大于样本中位数,说明数据中存在较大的极端值;反之,说明数据中不存在较大的极端值.
例2 某学校要定制高一年级的校服,学生根据厂家提供的参考身高选择校服规格. 根据统计,高一年级女生需要不同规格校服的频数如下表所示:
校服规格 155 160 165 170 175 合计
频数 39 64 167 90 26 386
分析:虽然校服规格是用数字表示的,但它们事实上是不同的类别,对于这样的分类数据,用众数作为这组数据的代表比较合适.
如果用一个量来代表该校高一年级女生所需校服的规格,那么在中位数、平均数和众数中,哪个量比较合适?试讨论用上表中的数据估计全国高一年级女生校服规格的合理性.
典例解析:用众数来描述数据的集中趋势
解:为了更直观地观察数据的特征,我们用条形图来表示表中的数据。
通过观察条形图可以发现,选择校服规格为“165”的女生频数最高,所以用众数165作为该校高一年级女生校服的规格比较合适.
由于全国各地的高一年级女生的身高存在一定的差异,所以用一个学校的数据估计全国高一年级女生的校服规格不合理.
众数只利用了出现次数最多的那个值的信息.众数只能告诉我们它比其他值出现的次数多,但并未告诉我们它比别的数值多的程度.因此,众数只能传递数据中的信息的很少的一部分,对极端值也不敏感.
新知探究:平均数、中位数、众数
新知探究:平均数、中位数、众数
问题4 根据平均数、中位数、众数各自的特点,我们应如何选择适合的统计量来表示数据的集中趋势?
(1)对数值型数据(如用水量、身高、收入、产量等)集中趋势的描述, 可以用
(2)对分类型数据(如校服规格、性别、产品质量等级等)集中趋势的描述,可以用
平均数、中位数
众数
新知探究:根据频率分布直方图估计平均数、中位数、众数
探究2 样本的平均数、中位数和众数可以分别作为总体的平均数、中位数和众数的估计,但在某些情况下我们无法获知原始的样本数据.
你能以图9.2-1中频率分布直方图提供的信息为例,给出估计方法吗
在频率分布直方图中,损失了大量的原始数据,我们无法知道每个组内的数据是如何分布的.
此时,通常假设它们在组内均匀分布.
这样就可以获得样本的平均数、中位数和众数的近似估计,进而估计总体的平均数、中位数和众数.
如何由频率分布直方图估计样本的平均数、中位数和众数?
新知探究:根据频率分布直方图估计平均数、中位数、众数
1. 根据频率分布直方图计算样本平均数:
因为样本平均数可以表示为数据与它的频率的乘积之和.
所以在频率分布直方图中,样本平均数可以用每个小矩形底边中点的横坐标与小矩形的面积的乘积之和近似代替.
月均用
水量/t
频率
组距
0.02
1.2 4.2 7.2 10.2 13.2 16.2 19.2 22.2 25.2 28.2
0
0.04
0.06
0.08
0.1
0.12
0.077
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
假设数据在组内均匀分布.
于是平均数的近似值为
↑小矩形面积(频率)
↓小矩形底边中点横坐标
这个结果与根据原始数据计算的样本平均数8.79相差不大.
新知探究:根据频率分布直方图估计平均数、中位数、众数
2. 根据频率分布直方图计算样本中位数:
根据中位数的意义,在样本中,有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数.
因此,在频率分布直方图中,中位数左边和右边的直方图的面积应该相等.
月均用水量/t
频率/组距
0.02
1.2 4.2 7.2 10.2 13.2 16.2 19.2 22.2 25.2 28.2
0
0.04
0.06
0.08
0.1
0.12
0.077
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
∴中位数落在区间[4.2,7.2)内
设中位数是x ,则
这个结果与根据原始数据求得的中位数6.8相差不大.
x-4.2
因此,中位数约为6.71.
(0.077+0.107)×3=0.552
月均用水量/t
频率/组距
0.02
1.2 4.2 7.2 10.2 13.2 16.2 19.2 22.2 25.2 28.2
0
0.04
0.06
0.08
0.1
0.12
0.077
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
3. 根据频率分布直方图计算样本众数:
根据众数定义得,在样本数据中出现次数最多数据就是众数.
因此在频率分布直方图中,我们常常把最高矩形的中点的横坐标作为众数的估计值.
因此,众数约为5.7.
新知探究:根据频率分布直方图估计平均数、中位数、众数
众数常用在描述分类型数据中,众数5.7让我们知道月均用水量在区间[4.2,7.2)的居民用户最多. 这个信息具有实际意义.
归纳小结
——找众数、中位数、平均数
众 数:
由频率分布直方图估计总体的集中趋势
中位数:
平均数:
【小结】
最高矩形的中点
中位数左边的直方图面积和右边的直方图面积相等
每个小矩形底边中点的横坐标与小矩形的面积的乘积之和
典例解析
例3 某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
(1)求这次测试数学成绩的众数;
(2)求这次测试数学成绩的中位数.
(3)求这次测试数学成绩的平均分.
(2)中位数
∴中位数落在区间[70,80)内,
设中位数是x ,则
∴中位数约为73.3
众数为最高矩形的中点
中位数左边的直方图面积和右边的直方图面积相等
0.05
0.15
0.2
0.3
典例解析
(3)平均数=
每个小矩形底边中点的横坐标与小矩形的面积的乘积之和
45
55
65
75
85
95
典例解析
理解升华
问题5 以上我们讨论了平均数、中位数和众数在刻画一组数据的集中趋势时的各自特点,并研究了用样本的特征量估计总体特征量的方法. 那么这种方法有什么不足?
这些特征量有时会被利用而产生误导.
问题6 假设你到人力市场去找工作,有一个企业老板告诉你,“我们企业员工的年平均收入是20万元”. 你如何理解这句话?
可能这个公司的工资水平普遍较高,也就是员工收入的中位数、众数与平均数差不多;
可能是绝大多数员工的年收入较低,而少数员工的年收入很高;在这种情况下,年收入的平均数就比中位数大得多.
尽管在后一种情况下,用中位数或众数比用平均数更合理些,但这个企业的老板为了招揽员工,却用了平均数.
所以,我们要强调“用数据说话”,但同时又要防止被数据误导. 这就需要掌握更多的统计知识和方法.
课堂小结
1、众数、中位数、平均数的定义及意义
2、平均数、中位数、众数在具体数据中的应用
3、在频率分布直方图中求众数、中位数、平均数
本节课的学习内容有哪些?
9.2.3 总体集中趋势的估计
第九章 统 计
9.2 用样本估计总体
新课导入
为了了解总体的情况,前面我们研究了如何通过样本的分布规律估计总体的分布规律.但有时候,我们可能不太关心总体的分布规律,而更关注总体取值在某一方面的特征.
例如,对于某县今年小麦的收成情况,我们可能会更关注该县今年小麦的总产量或平均每公顷的产量,而不是产量的分布;对于一个国家国民的身高情况,我们可能会更关注身高的平均数或中位数,而不是身高的分布;等等.
在初中的学习中我们已经了解到,平均数、中位数和众数等都是刻画“中心位置”的量,它们从不同角度刻画了一组数据的集中趋势. 那你是否还记得平均数、中位数、众数是什么吗?这些统计量刻画了数据的什么特点?
众数:
中位数:
当数据个数是奇数时,处在最中间的数是中位数;
当数据个数是偶数时,最中间两个数的平均数是中位数.
(第50百分位数)
平均数:
平均数、中位数、众数的定义
复习回顾
一组数据中出现次数最多的数.
一组数据按从小到大排序,
注意单位(t)
下面我们通过具体实例进一步了解这些量的意义,探究它们之间的联系与区别,并根据样本的集中趋势估计总体的集中趋势.
例1 利用9.2.1节中100户居民用户的月均用水量的调查数据,计算样本数据的平均数和中位数,并据此估计全市居民用户月均用水量的平均数和中位数。
9.0 13.6 14.9 5.9 4.0 7.1 6.4 5.4 19.4 2.0 2.2 8.6 13.8 5.4 10.2 4.9 6.8 14.0 2.0 10.5 2.1 5.7 5.1 16.8 6.0 11.1 1.3 11.2 7.7 4.9 2.3 10.0 16.7 12.0 12.4 7.8 5.2 13.6 2.4 22.4 3.6 7.1 8.8 25.6 3.2 18.3 5.1 2.0 3.0 12.0 22.2 10.8 5.5 2.0 24.3 9.9 3.6 5.6 4.4 7.9 5.1 24.5 6.4 7.5 4.7 20.5 5.5 15.7 2.6 5.7 5.5 6.0 16.0 2.4 9.5 3.7 17.0 3.8 4.1 2.3 5.3 7.8 8.1 4.3 13.3 6.8 1.3 7.0 4.9 1.8 7.1 28.0 10.2 13.8 17.9 10.1 5.5 4.6 3.2 21.6
解:① 根据已知100户居民用户月均用水量的数据,可得样本平均数为
即100户居民的月均用水量的平均数为8. 79 t.
新知探究:平均数、中位数、众数
新知探究:平均数、中位数、众数
解:
②将样本数据按从小到大排序,结果如下:
1.3 1.3 1.8 2.0 2.0 2.0 2.0 2.1 2.2 2.3 2.3 2.4 2.4 2.6 3.0 3.2 3.2 3.6 3.6 3.7 3.8 4.0 4.1 4.3 4.4 4.6 4.7 4.9 4.9 4.9 5.1 5.1 5.1 5.2 5.3 5.4 5.4 5.5 5.5 5.5 5.5 5.6 5.7 5.7 5.9 6.0 6.0 6.4 6.4 6.8 6.8 7.0 7.1 7.1 7.1 7.5 7.7 7.8 7.8 7.9 8.1 8.6 8.8 9.0 9.5 9.9 10.0 10.1 10.2 10.2 10.5 10.8 11.1 11.2 12.0 12.0 12.4 13.3 13.6 13.6 13.8 13.8 14.0 14.9 15.7 16.0 16.7 16.8 17.0 17.9 18.3 19.4 20.5 21.6 22.2 22.4 24.3 24.5 25.6 28.0
6.8 6.8
由上述数据可得,第50个数和第51个数均为6.8,由中位数的定义,可得,100户居民的月均用水量的中位数是6.8t.
因为数据是抽自全市居民户的简单随机样本,所以我们可以据此估计全市居民用户的月均用水量约为8.79 t,其中位数约为6.8 t,众数是2.0和5.5t.
问题1 设某个居民小区有2000户,你能估计该小区的月用水总量吗?
③由众数的定义,可得100户居民的月均用水量的众数是
2.0和5.5 t.
问题2 小明用统计软件计算了100户居民用水量的平均数和中位数. 但在录入数据时,不小心把一个数据7.7录成了77. 请计算录入数据的平均数和中位数,并与真实的样本平均数和中位数作比较. 哪个量的值变化更大?
新知探究:平均数、中位数、众数
77
8.79t→9.483t
6.8t→6.8t
新知探究:平均数、中位数、众数
问题3 你能解释出现问题2中现象的原因吗?
中位数
平均数
(1)平均数有所变化;样本的平均数与每个数据有关,样本中的每一个数据的变化都能引起平均数的变化;
(2)中位数只与样本数据中间位置的一个或两个值有关,与其他数据无关,所以不是任何一个样本数据的改变都会引起中位数的改变.
与中位数比较,平均数反映出样本数据中的更多信息,对样本中的极端值更加敏感。
8.79t→9.483t
6.8t→6.8t
(1)平均数和中位数应该大体上差不多;
(2)平均数大于中位数;(右边“拖尾”)
(3)平均数小于中位数. (左边“拖尾”)
在直方图中,平均数总在“长尾巴”那边
平均数、中位数、众数刻画一组数据的集中趋势的特点
探究1 平均数和中位数都描述了数据的集中趋势,它们的大小关系和数据分布的形态有关.在下图的三种频率分布直方图形态中,平均数和中位数的大小存在什么关系?
新知探究:平均数与中位数的大小与数据分布形态的关系
追问 如果一组数据的平均数和中位数相差较大,能说明什么呢?
新知探究:平均数、中位数、众数
如果一组数据的平均数和中位数相差较大,那么可以推断这组数据一定是不对称的.
如果样本平均数大于样本中位数,说明数据中存在较大的极端值;反之,说明数据中不存在较大的极端值.
例2 某学校要定制高一年级的校服,学生根据厂家提供的参考身高选择校服规格. 根据统计,高一年级女生需要不同规格校服的频数如下表所示:
校服规格 155 160 165 170 175 合计
频数 39 64 167 90 26 386
分析:虽然校服规格是用数字表示的,但它们事实上是不同的类别,对于这样的分类数据,用众数作为这组数据的代表比较合适.
如果用一个量来代表该校高一年级女生所需校服的规格,那么在中位数、平均数和众数中,哪个量比较合适?试讨论用上表中的数据估计全国高一年级女生校服规格的合理性.
典例解析:用众数来描述数据的集中趋势
解:为了更直观地观察数据的特征,我们用条形图来表示表中的数据。
通过观察条形图可以发现,选择校服规格为“165”的女生频数最高,所以用众数165作为该校高一年级女生校服的规格比较合适.
由于全国各地的高一年级女生的身高存在一定的差异,所以用一个学校的数据估计全国高一年级女生的校服规格不合理.
众数只利用了出现次数最多的那个值的信息.众数只能告诉我们它比其他值出现的次数多,但并未告诉我们它比别的数值多的程度.因此,众数只能传递数据中的信息的很少的一部分,对极端值也不敏感.
新知探究:平均数、中位数、众数
新知探究:平均数、中位数、众数
问题4 根据平均数、中位数、众数各自的特点,我们应如何选择适合的统计量来表示数据的集中趋势?
(1)对数值型数据(如用水量、身高、收入、产量等)集中趋势的描述, 可以用
(2)对分类型数据(如校服规格、性别、产品质量等级等)集中趋势的描述,可以用
平均数、中位数
众数
新知探究:根据频率分布直方图估计平均数、中位数、众数
探究2 样本的平均数、中位数和众数可以分别作为总体的平均数、中位数和众数的估计,但在某些情况下我们无法获知原始的样本数据.
你能以图9.2-1中频率分布直方图提供的信息为例,给出估计方法吗
在频率分布直方图中,损失了大量的原始数据,我们无法知道每个组内的数据是如何分布的.
此时,通常假设它们在组内均匀分布.
这样就可以获得样本的平均数、中位数和众数的近似估计,进而估计总体的平均数、中位数和众数.
如何由频率分布直方图估计样本的平均数、中位数和众数?
新知探究:根据频率分布直方图估计平均数、中位数、众数
1. 根据频率分布直方图计算样本平均数:
因为样本平均数可以表示为数据与它的频率的乘积之和.
所以在频率分布直方图中,样本平均数可以用每个小矩形底边中点的横坐标与小矩形的面积的乘积之和近似代替.
月均用
水量/t
频率
组距
0.02
1.2 4.2 7.2 10.2 13.2 16.2 19.2 22.2 25.2 28.2
0
0.04
0.06
0.08
0.1
0.12
0.077
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
假设数据在组内均匀分布.
于是平均数的近似值为
↑小矩形面积(频率)
↓小矩形底边中点横坐标
这个结果与根据原始数据计算的样本平均数8.79相差不大.
新知探究:根据频率分布直方图估计平均数、中位数、众数
2. 根据频率分布直方图计算样本中位数:
根据中位数的意义,在样本中,有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数.
因此,在频率分布直方图中,中位数左边和右边的直方图的面积应该相等.
月均用水量/t
频率/组距
0.02
1.2 4.2 7.2 10.2 13.2 16.2 19.2 22.2 25.2 28.2
0
0.04
0.06
0.08
0.1
0.12
0.077
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
∴中位数落在区间[4.2,7.2)内
设中位数是x ,则
这个结果与根据原始数据求得的中位数6.8相差不大.
x-4.2
因此,中位数约为6.71.
(0.077+0.107)×3=0.552
月均用水量/t
频率/组距
0.02
1.2 4.2 7.2 10.2 13.2 16.2 19.2 22.2 25.2 28.2
0
0.04
0.06
0.08
0.1
0.12
0.077
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
3. 根据频率分布直方图计算样本众数:
根据众数定义得,在样本数据中出现次数最多数据就是众数.
因此在频率分布直方图中,我们常常把最高矩形的中点的横坐标作为众数的估计值.
因此,众数约为5.7.
新知探究:根据频率分布直方图估计平均数、中位数、众数
众数常用在描述分类型数据中,众数5.7让我们知道月均用水量在区间[4.2,7.2)的居民用户最多. 这个信息具有实际意义.
归纳小结
——找众数、中位数、平均数
众 数:
由频率分布直方图估计总体的集中趋势
中位数:
平均数:
【小结】
最高矩形的中点
中位数左边的直方图面积和右边的直方图面积相等
每个小矩形底边中点的横坐标与小矩形的面积的乘积之和
典例解析
例3 某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
(1)求这次测试数学成绩的众数;
(2)求这次测试数学成绩的中位数.
(3)求这次测试数学成绩的平均分.
(2)中位数
∴中位数落在区间[70,80)内,
设中位数是x ,则
∴中位数约为73.3
众数为最高矩形的中点
中位数左边的直方图面积和右边的直方图面积相等
0.05
0.15
0.2
0.3
典例解析
(3)平均数=
每个小矩形底边中点的横坐标与小矩形的面积的乘积之和
45
55
65
75
85
95
典例解析
理解升华
问题5 以上我们讨论了平均数、中位数和众数在刻画一组数据的集中趋势时的各自特点,并研究了用样本的特征量估计总体特征量的方法. 那么这种方法有什么不足?
这些特征量有时会被利用而产生误导.
问题6 假设你到人力市场去找工作,有一个企业老板告诉你,“我们企业员工的年平均收入是20万元”. 你如何理解这句话?
可能这个公司的工资水平普遍较高,也就是员工收入的中位数、众数与平均数差不多;
可能是绝大多数员工的年收入较低,而少数员工的年收入很高;在这种情况下,年收入的平均数就比中位数大得多.
尽管在后一种情况下,用中位数或众数比用平均数更合理些,但这个企业的老板为了招揽员工,却用了平均数.
所以,我们要强调“用数据说话”,但同时又要防止被数据误导. 这就需要掌握更多的统计知识和方法.
课堂小结
1、众数、中位数、平均数的定义及意义
2、平均数、中位数、众数在具体数据中的应用
3、在频率分布直方图中求众数、中位数、平均数
本节课的学习内容有哪些?
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
