2024年中考数学复习--将军饮马最值模型(含解析)
文档属性
| 名称 | 2024年中考数学复习--将军饮马最值模型(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-12 00:00:00 | ||
图片预览



文档简介
将军饮马最值模型
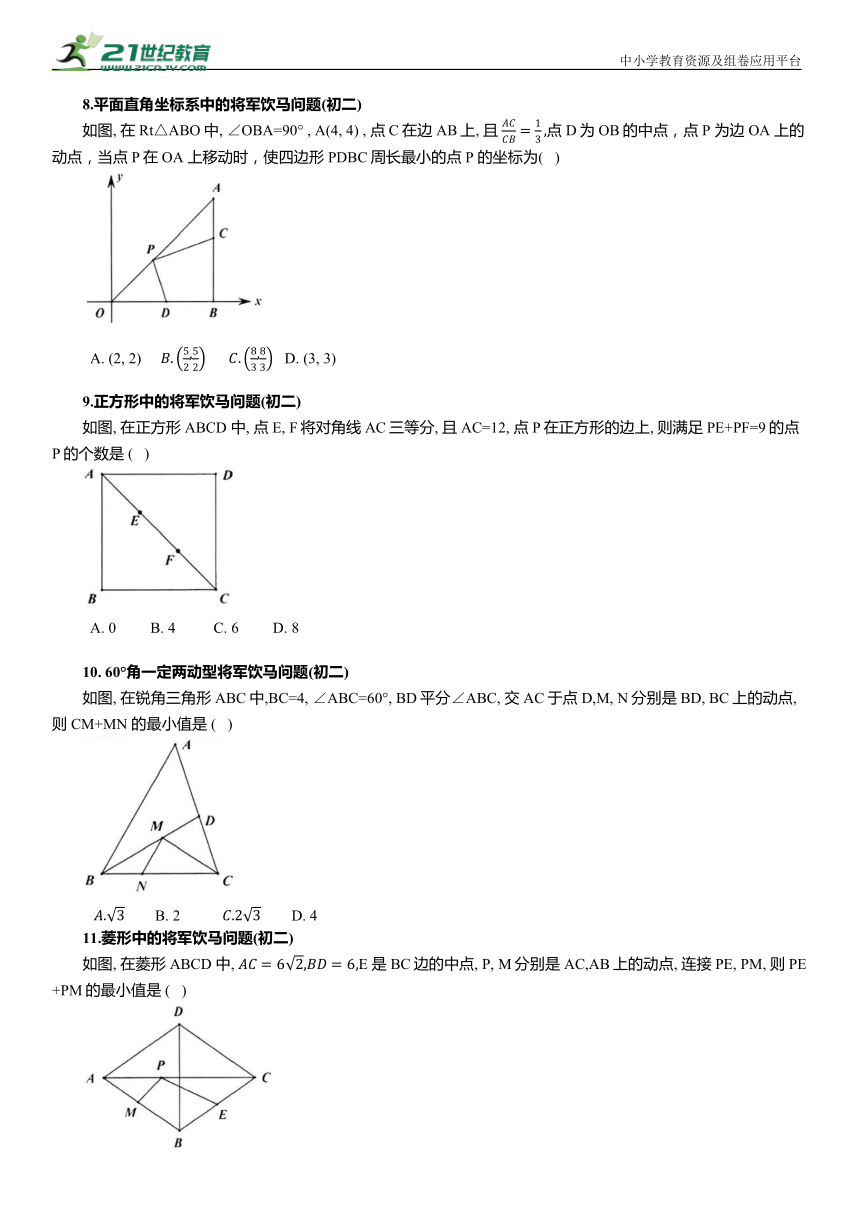
1.正方形中的将军饮马最小值问题(初二)
如图,正方形ABCD的对角线交于点O,点E是直线BC上一动点. 若AB=4,则AE+OE 的最小值是 ( )
2.直角三角形中的将军饮马 垂线段最短(初二)
已知在Rt△ACB中, ∠C=90°, ∠ABC=75° , AB=5, 点E为边AC上的动点,点F 为边 AB上的动点, 则线段 FE+EB 的最小值是 ( )
3.矩形中的将军饮马最小值问题(初二)
如图, 点P 为矩形ABCD的对角线AC上一动点, 点 E 为BC 的中点, 连接PE, PB,若 则PE+PB 的最小值为 .
4.正方形中的将军饮马最小值问题(初三)
如图, 正方形ABCD的边长为5, E为AD的中点, P 为CE 上一动点, 则 的最小值为 .
中小学教育资源及组卷应用平台
5. 正方形中的将军饮马与隐形圆综合题(初三)
如图,动点M在边长为2的正方形 ABCD 内,且 ,P 是CD边上的一个动点,学习笔记:E 是 AD边的中点, 则线段 PE+PM的最小值为 ( )
6. 平面直角坐标系中造桥选址问题(初二)
在平面直角坐标系中,长为2的线段CD(点D在点C右侧)在x轴上移动,A(O,2) , B(0, 4) , 连接AC, BD, 则AC+BD的最小值为 ( )
7.正方形中的将军饮马变式题(初二)
如图, 正方形ABCD 的边长为4, 点M在边BC 上, P 为正方形内(含边上)一点, 且 正方形 ABCD,G 为边CD 上一动点, 连接MG, GP, 则 的最小值为 .
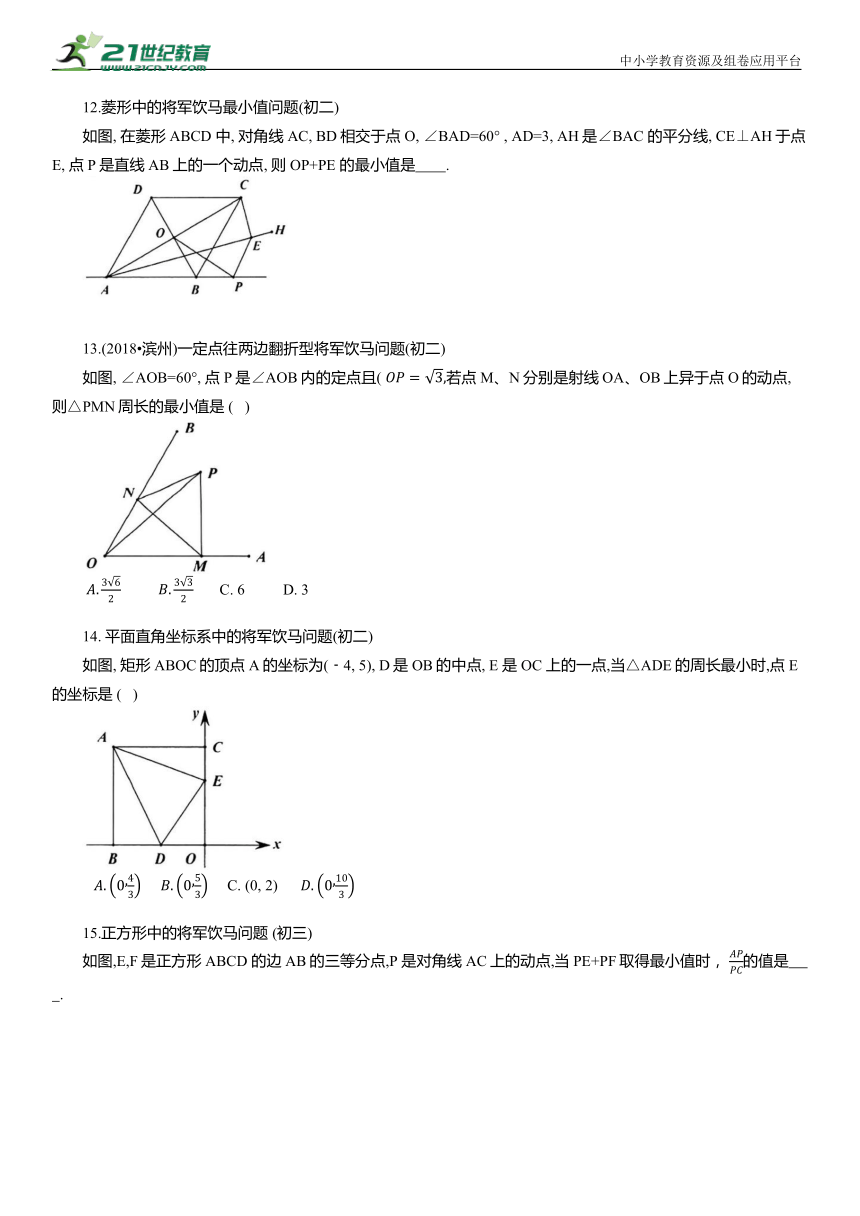
8.平面直角坐标系中的将军饮马问题(初二)
如图, 在Rt△ABO中, ∠OBA=90° , A(4, 4) , 点C在边AB上, 且 点D为OB的中点,点P 为边OA 上的动点,当点P在OA 上移动时,使四边形 PDBC周长最小的点P 的坐标为( )
A. (2, 2) D. (3, 3)
9.正方形中的将军饮马问题(初二)
如图, 在正方形ABCD 中, 点E, F将对角线AC三等分, 且AC=12, 点P在正方形的边上, 则满足PE+PF=9的点P的个数是 ( )
A. 0 B. 4 C. 6 D. 8
10. 60°角一定两动型将军饮马问题(初二)
如图, 在锐角三角形ABC中,BC=4, ∠ABC=60°, BD平分∠ABC, 交AC于点D,M, N分别是BD, BC上的动点, 则 CM+MN 的最小值是 ( )
B. 2 D. 4
11.菱形中的将军饮马问题(初二)
如图, 在菱形 ABCD 中, E 是 BC边的中点, P, M分别是 AC,AB上的动点, 连接PE, PM, 则PE+PM的最小值是 ( )
A. 6 D. 4.5
12.菱形中的将军饮马最小值问题(初二)
如图, 在菱形ABCD 中, 对角线AC, BD相交于点O, ∠BAD=60° , AD=3, AH是∠BAC 的平分线, CE⊥AH于点E, 点P是直线AB上的一个动点, 则 OP+PE 的最小值是 .
13.(2018 滨州)一定点往两边翻折型将军饮马问题(初二)
如图, ∠AOB=60°, 点P是∠AOB内的定点且( 若点M、N分别是射线OA、OB上异于点O的动点, 则△PMN周长的最小值是 ( )
C. 6 D. 3
14. 平面直角坐标系中的将军饮马问题(初二)
如图, 矩形ABOC的顶点A的坐标为(﹣4, 5), D是OB的中点, E 是OC 上的一点,当△ADE的周长最小时,点E 的坐标是 ( )
C. (0, 2)
15.正方形中的将军饮马问题 (初三)
如图,E,F是正方形ABCD 的边AB的三等分点,P 是对角线AC上的动点,当PE+PF取得最小值时, 的值是 .
16.等边三角形中的将军饮马问题(初二)
如图, 是等边三角形, N 是 AB的中点, AD 是 BC边上的中线, M是 AD上的一个动点, 连接BM, MN, 则 BM+MN的最小值是 .
17. 菱形中的将军饮马问题(初二)
如图, 在菱形ABCD 中, Q为AB的中点, P 为对角线BD上的任意一点,则AP+PQ的最小值为 .
18.平面直角坐标系中造桥选址问题(初二)
如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A,C 分别在 x轴, y轴上, B, D两点坐标分别为B(﹣4, 6), D(0, 4) , 线段EF在边OA上移动,保持EF=3, 当四边形 BDEF 的周长最小时,点E 的坐标为 .
19. 正方形中的将军饮马问题 (初二)
如图, 正方形ABCD 的边长为8, 点M在DC 上且 , N是 AC上的一动点, 则DN+MN 的最小值是 .
20. 正方形中将军饮马综合题(初三)
如图, 正方形 ABCD 中, AB=1, 连接AC, ∠ACD 的角平分线交AD于点E, 在AB上截取 AF=DE, 连接DF, 分别交 CE, CA于点G, H, 点 P 是线段GC上的动点,PQ⊥AC 于点Q, 连接PH. 下列结论: ①CE⊥DF; ②DE+DC=AC; ③EA= AH;④PH+PQ 的最小值是 其中所有正确结论的序号是 .
21菱形中的两点之间线段最短 (初二)
如图, 四边形ABCD是菱形,对角线AC, BD相交于点O, 点P是 AC 上一动点, 点 E 是 AB的中点, 则PD+PE 的最小值为 .
22.等腰三角形中的将军饮马周长最小值问题(初二)
如图, 等腰△ABC 的底边BC=20, 面积为120, 点D在BC边上, 且( 直线EF 是腰AC的垂直平分线,若点M在EF上运动,则 周长的最小值为 .
23.平面直角坐标系中造桥选址问题(初二)
如图, 在平面直角坐标系中,已知A(3, 6), B(﹣2, 2), 在x轴上取两点C,D(点C 在点 D左侧), 且始终保持CD=1, 线段CD在 x轴上平移, 当AD+BC 的值最小时,点C 的坐标为 .
1.解:如图,作点A 关于直线 BC的对称点 A',连接A'O, 其与BC的交点即为点 E, 再作 OF⊥AB交AB于点 F,
∵ A 与 A'关于 BC 对称,
∴ AE=A'E, AE+OE=A'E+OE,
∴ 当且仅当A',O,E三点共线时和最小,如图所示,此时 ,则 A'O 即为所求.
∵正方形ABCD,点O为对角线的交点,
∵A 与A'关于 BC对称, ∴AB=BA'=4,
∴FA'=FB+BA'=2+4=6,
在 Rt△OFA'中, 故选: D.
2. 简解: 过点B作关于 AC的对称点 B', 连接B'E,由对称性质得: AB'=AB=5, EB=EB'
∴FE+EB=FE+EB′, ∴当B′、E、F三点共线且垂直AB时有最小值,如图,B'D 即为所求的最小值,
∵∠C=90° , ∠ABC=75° ∴∠BAC=15°
∴ 在Rt△AB'D中, ∠B'AD=2∠BAC=30°,
故选: B.
3. 解: 如图, 作点B 关于 AC的对称点B', 交AC 于点F, 连接EF, 由对称性可知, PB=PB'
, 当B' 、P、E三点共线时,则B' E的长度即为PE+PB的最小值.
∵四边形ABCD为矩形,
∴AB=CD=4, ∠ABC=90° ,
在 Rt△ABC 中,
∴∠ACB=30° ,
由对称的性质可知, B'B=2BF, B'B⊥AC,
∵BE=BF, ∠CBF=60°, ∴△BEF是等边三角形,
∴BE=BF=B'F, ∴△BEB'是直角三角形,
∴PE+PB 的最小值为6, 故答案为: 6.
4. 解: 作 B 点关于 EC 的对称点F, BF 交 EC于点 H,过F 点作 FG⊥BC 交 BC 的延长线于点G, 连接PF.
由对称性质得: BP=FP, ∴AP+BP=AP+PF,
当A、P、F三点共线时, AF 即为AP+BP的最小值,
∵E 点是 AD的中点, 正方形ABCD的边长为5,
∵BH⊥EC, ∴∠BHC=90° ,
∴BH=2HC, 在 Rt△BCH中, ( 设HC=a, 则 BH=2a, 且已知BC=5,
在 Rt△BGF中,同理可得, BG=2FG, ∴GF=4, BG=8,过点 F 作 FM⊥AB交于 M,
依题意得: MF=BG=8, AM=1,
在 Rt△AFM 中,
∴AP+BP的最小值为 故答案为:
5.解:作点 E 关于 DC的对称点 E', 设AB 的中点为点 O,连接OE', 交 DC于点 P, 连接PE, 如图:
∵动点M在边长为2的正方形ABCD 内, 且AM⊥BM,
∴点 M在以AB 为直径的半圆上,
∵正方形 ABCD的边长为2,
∴AD=AB=2, ∠DAB=90° ,
∵E是AD的中点,
∵作点 E 关于 DC 的对称点 E',
∴DE'=DE=1, PE=PE', ∴AE'=AD+DE'=2+1=3,
∴ PE+PM=PE'+PM, 连接OE', 于 CD 交于P, 与半圆交于点 M, 此时E'M 的值, 即为PE+PM的最小值.在 Rt△AOE'中, 故选: A.
6. 简解: 如图, 作 BDCE, 则EC=BD.
∴ AC+BD=AC+EC,根据将军饮马原理,过点A作x 轴的对称点 A′, 则AC=A′C.
∴ AC+BD=AC+EC=A'C+EC,
当E、C、A'三点共线时,有最小值, 即为所求, ∴AC+BD的最小值为 故选: B.
7. 解: 过点P作EF∥AB, 分别交AD, BC于点E, F,
∵四边形ABCD是正方形,
∴四边形ABFE和四边形EFCD 都是矩形,
正方形ABCD, 正方形ABCD的边长为4,
解得FB=2,
∴CF=BC-FB=4-2=2=FB,
即 F 是 BC的中点, 且P 点在线段EF 上运动.
作点 M关于 CD的对称点 M' , 连接M' G,
则M' G=MG, M' C=MC=1,
∴MG+GP=M' G+GP≥M' F,
∴MG+GP的最小值为M' F 的长,
∵M' F=M' C+CF=1+2=3,
∴MG+GP的最小值为3, 故答案为: 3.
8. 解: ∵在Rt△ABO中, ∠OBA=90°, A(4, 4), 点D为OB的中点, ∴BC=3, OD=BD=2, ∴D(2, 0), C(4,3),作D关于直线OA的对称点E,连接EC交OA于P,则此时, 四边形PDBC周长最小, E(0,2),
∵直线OA 的解析式为y=x,设直线EC的解析式为 解得:
∴直线EC的解析式为 解 得, 故选: C.
9. 解: 如图, 作点F关于 BC的对称点 M, 连接FM交BC于点N, 连接EM, 交BC于点 H
∵点E, F将对角线AC三等分, 且AC=12,
∴EC=8, FC=4=AE,
∵点M 与点 F 关于 BC对称
∴CF=CM=4, ∠ACB=∠BCM=45° ∴∠ACM=90°
则在线段BC存在点H到点E和点F的距离之和最小为 ,在点 H右侧,当点 P 与点 C 重合时, 则PE+PF=12
∴点 P 在 CH上时, 在点H左侧,当点 P 与点 B重合时,
∵AB=BC, AE=CF, ∠BAE=∠BCF,
∴△ABE≌△CBF(SAS)∴BE=BF=2 ,
∴点 P 在 BH 上时,
∴在线段BC上点H的左右两边各有一个点P,使得PE+PF=9, 同理在线段AB, AD, CD上都存在两个点P, 使得PE+PF=9. 即共有8个点 P 满足PE+PF=9, 故选: D.
10. 简解: 如图, 在 BA 上截取BE=BC, 连接ME,∵∠ABC的平分线交AC于点 D, ∴∠EBM=∠NBM,在△BME与△BMC中, △BME≌△BMC(SAS),∴ME=MC. ∴CM+MN=CM+ME.
当N、M、E三点共线且垂直BC时,取最小值,EF即为所求最小值: 故选: C.
11. 解: 如图, 作点E关于AC的对称点 E' , 过点 E'作 E' F⊥AB 于点 F, 则E' F 即为所求最小值,∵四边形ABCD 是菱形, ∴点E' 在 CD 上, 由 得: 解得: E' F 即 PE+PM的最小值是 故选: C.
12. 解: 连接OE, 过点O作OF⊥AB, 垂足为F, 并延长到点 O' , 使O' F=OF, 连接O' E交直线AB 于点P,连接OP, ∴AP 是OO'的垂直平分线, ∴OP=O' P,∴OP+PE=O'P+PE, 当O' 、P、E三点共线时, O' E即为OP+PE的值最小,
∵四边形ABCD 是菱形, ∴AD=AB=3, OA=OC=
∵∠BAD=60°, ∴△ADB是等边三角形,
∵CE⊥AH, ∴∠AEC=90° ,
∵AE平分∠CAB, ∴∠OAE=∠EAB,
∴∠OEA=∠EAB, ∴OE∥AB,
∴∠EOF=∠AFO=90°,
在 Rt△AOF 中,
在 Rt△EOO' 中,
∴OP+PE的最小值为 故答案为:
13. 解: 作P 点分别关于OA、OB的对称点 C、D, 连接CD分别交OA、 OB于M、N, 则MP=MC, NP=ND,OP=OD=OC= ,∠BOP=∠BOD,∠AOP=∠AOC,∴PN+PM+MN=ND+MN+MC=DC, ∠COD=∠BOP+∠BOD+∠AOP+∠AOC=2∠AOB=120°,
∴此时△PMN周长最小, 作 OH⊥CD 于H, 则CH=DH,
故选: D.
14. 解:如图, 作A关于y轴的对称点A', 连接A'D交y轴于E, 则此时, △ADE的周长最小,
∵四边形 ABOC 是矩形,
∴AC∥OB, AC=OB, ∵A点的坐标为(-4, 5) ,
∴A′ (4,5), B(-4,0), ∵D是OB的中点, ∴D(-2, 0),设直线DA'的解析式为
∴直线DA'的解析式为 当x=0时, 故选: B .
15. 解: 作点 E 关于 AC 的对称点 E', 连接 FE'交 AC于点 P', 连接PE',
∴PE=PE', ∴PE+PF=PE'+PF≥E'F,故当PE+PF 取得最小值时, 点 P 位于点 P'处,
∴当PE+PF取得最小值时, 求 的值,只要求出 的值即可.
∵正方形ABCD 是关于 AC 所在直线轴对称,
∴点 E 关于 AC 所在直线对称的对称点 E'在 AD 上,且 AE'=AE, 过点F 作FG⊥AB 交AC 于点G,则∠GFA=90° ,
∵四边形 ABCD 是正方形,
∴∠DAB=∠B=90°, ∠CAB=∠ACB=45° ,
∴FG∥BC∥AD, ∠AGF=∠ACB=45° , ∴GF=AF,
∵E, F是正方形ABCD的边AB的三等分点,
又∵FG∥
故答案为: .
16.解: 如下图, 连接CM, CN,
∵△ABC是等边三角形, AD 是中线, ∴AD⊥BC, BD=CD, ∴AD是BC的垂直平分线, ∴BM=CM, ∴BM+MN=CM+MN, 即当点C、M、N三点共线时,BM+MN最小值为CN的长,
∵点 N 是 AB 的中点,
最小值为: 故答案为:
17. 解: 如图, 连接 PC, AC, CQ. ∵四边形ABCD 是菱形, ∴∠ABP=∠PBC, 在△ABP和△CBP中,△ABP≌△CBP (SAS) , ∴PA=PC,
∵AB∥CD, ∴∠ABC+∠BCD=180°,
∴∠ABC=180° -120° =60°, ∵AB=BC,
∴△ABC是等边三角形, ∵AQ=QB, ∴CQ⊥AB,
的最小值为
故答案为:
18. 解: 在 BC上截取BH=3, 作点 D 关于x轴的对称点G, 连接GH交AO于点E, ∴BH=EF=3, BC∥AO, ∴四边形BHEF是平行四边形,
∴BF=EH,∵点D与点G关于x轴对称,
∴DE=GE, 点 G坐标为 (0, -4),
∵四边形BDEF的周长=EF+BF+BD+DE,
∴四边形BDEF的周长=EF+EH+EG+BD,
∵EF和BD 是定值, ∴当EH+GE有最小值时, 四边形BDEF的周长有最小值, ∴当点E, 点H, 点 G 共线时,EH+GE有最小值, ∵点B(-4, 6) , ∴点H(-1, 6),设直线GH的解析式为y=kx+b, 把点G(0, -4) 、点H(--1,6)代入,待定系数法可得,直线 GH 的解析式为:y=-10x-4, ∴当y=0时, ∴点 故答案为:
19.解:∵正方形是轴对称图形,点 B 与点 D 是关于直线AC为对称轴的对称点, ∴连接BN, BD, ∴BN=ND,∴DN+MN=BN+MN, 连接BM交AC于点 P,
∵点 N为AC上的动点,由三角形两边和大于第三边可知, 当点N运动到点 P时, BN+MN=BP+PM=BM,BN+MN的最小值为BM的长度,
∵四边形ABCD 为正方形,
∴BC=CD=8, CM=8-2=6, ∠BCM=90° ,
∴BM=10, ∴DN+MN的最小值是10. 故答案为: 10.
20. 解:∵正方形ABCD, ∴CD=AD,∠CDE=∠DAF=90° , ∴∠ADF+∠CDF=90° ,在△CDE和△DAF中, 易证△CDE≌△DAF(ASA) ,
∴∠DCE=∠ADF, ∴∠DCE+∠CDF=90°,
∴∠DGC=90°, ∴CE⊥DF, 故①正确;
∵CE平分∠ACD, ∴∠DCE=∠HCG, 在△GCD和△GCH中, 易证∴△GCD≌△GCH(ASA) ,
∴CD=CH, ∠CDH=∠CHD,
∵正方形ABCD, ∴CD∥AB, ∴∠CDF=∠AFD,
∴∠CHD=∠AFD, ∵∠CHD=∠AHF,
∴∠AFD=∠AHF, ∴AF=AH,
∴AC=AH+CH=AF+CD=DE+CD, 故②正确,设DE=AF=AH=a,
∵∠AHF=∠DHC, ∠CDF=∠AFH,
- 故③错误;
∵△GCD≌△GCH, ∴DG=GH,
∵CE⊥DF, ∴CG垂直平分DH, ∴DP=PH,当DQ⊥HC时, PH+PQ=DP+PQ有最小值,过点 D作DM⊥HC,则DM的长度为PH+PQ的最小值,
故④正确. 故答案为: ①②④.
21. 解: 如图, 连接DE, ∵四边形ABCD 是菱形, 对角线AC, BD 相交于点 O,
即△ABD
是等边三角形,又∵E 是 AB 的中点,
∵DP+PE≥DE, ∴PD+PE 的最小值为 DE 的长, 即PD+PE的最小值为: 故答案为:
22. 解: 如图, 作AH⊥BC于 H, 连接AM,
∵EF 垂直平分线段AC, ∴MA=MC, ∴DM+MC=AM+MD, ∴当A、D、M共线时, DM+MC的值最小,
∵等腰△ABC的底边BC=20, 面积为120, AH⊥BC,
∴BH=CH=10, AH=12, ∴DH=CH--CD=5,
∴AD=13, ∴DM+MC的最小值为13,
∴△CDM周长的最小值=13+5=18, 故答案为18.
23. 解: 把A(3, 6) 向左平移1得A' (2, 6) , 作点B 关于x轴的对称点B' , 连接B' A' 交x轴于 C, 在x轴上取点 D(点C在点 D左侧) , 使CD=1, 连接AD,则AD+BC的值最小,∵B(-2,2), ∴B′ (-2, -2),由A' (2, 6) 、B' (-2, -2)的坐标, 得直线 B' A'的解析式为y=2x+2,当y=0时,x=-1,∴C(-1,0),故答案为: (-1, 0) .
24. 解: 如图, 作点 D关于 OB的对称点 D', 连接D'C交 OB于点 E', 连接E' D、OD' ,
此时E' C+E' D 最小, 即: E' C+E' D=CD' , 由题意得, ∠COD=∠DOB=∠BOD′ =30° , ∴∠COD′ =
CD弧的长 ∴阴影部分周长的最小值为 故答案为:
1.正方形中的将军饮马最小值问题(初二)
如图,正方形ABCD的对角线交于点O,点E是直线BC上一动点. 若AB=4,则AE+OE 的最小值是 ( )
2.直角三角形中的将军饮马 垂线段最短(初二)
已知在Rt△ACB中, ∠C=90°, ∠ABC=75° , AB=5, 点E为边AC上的动点,点F 为边 AB上的动点, 则线段 FE+EB 的最小值是 ( )
3.矩形中的将军饮马最小值问题(初二)
如图, 点P 为矩形ABCD的对角线AC上一动点, 点 E 为BC 的中点, 连接PE, PB,若 则PE+PB 的最小值为 .
4.正方形中的将军饮马最小值问题(初三)
如图, 正方形ABCD的边长为5, E为AD的中点, P 为CE 上一动点, 则 的最小值为 .
中小学教育资源及组卷应用平台
5. 正方形中的将军饮马与隐形圆综合题(初三)
如图,动点M在边长为2的正方形 ABCD 内,且 ,P 是CD边上的一个动点,学习笔记:E 是 AD边的中点, 则线段 PE+PM的最小值为 ( )
6. 平面直角坐标系中造桥选址问题(初二)
在平面直角坐标系中,长为2的线段CD(点D在点C右侧)在x轴上移动,A(O,2) , B(0, 4) , 连接AC, BD, 则AC+BD的最小值为 ( )
7.正方形中的将军饮马变式题(初二)
如图, 正方形ABCD 的边长为4, 点M在边BC 上, P 为正方形内(含边上)一点, 且 正方形 ABCD,G 为边CD 上一动点, 连接MG, GP, 则 的最小值为 .
8.平面直角坐标系中的将军饮马问题(初二)
如图, 在Rt△ABO中, ∠OBA=90° , A(4, 4) , 点C在边AB上, 且 点D为OB的中点,点P 为边OA 上的动点,当点P在OA 上移动时,使四边形 PDBC周长最小的点P 的坐标为( )
A. (2, 2) D. (3, 3)
9.正方形中的将军饮马问题(初二)
如图, 在正方形ABCD 中, 点E, F将对角线AC三等分, 且AC=12, 点P在正方形的边上, 则满足PE+PF=9的点P的个数是 ( )
A. 0 B. 4 C. 6 D. 8
10. 60°角一定两动型将军饮马问题(初二)
如图, 在锐角三角形ABC中,BC=4, ∠ABC=60°, BD平分∠ABC, 交AC于点D,M, N分别是BD, BC上的动点, 则 CM+MN 的最小值是 ( )
B. 2 D. 4
11.菱形中的将军饮马问题(初二)
如图, 在菱形 ABCD 中, E 是 BC边的中点, P, M分别是 AC,AB上的动点, 连接PE, PM, 则PE+PM的最小值是 ( )
A. 6 D. 4.5
12.菱形中的将军饮马最小值问题(初二)
如图, 在菱形ABCD 中, 对角线AC, BD相交于点O, ∠BAD=60° , AD=3, AH是∠BAC 的平分线, CE⊥AH于点E, 点P是直线AB上的一个动点, 则 OP+PE 的最小值是 .
13.(2018 滨州)一定点往两边翻折型将军饮马问题(初二)
如图, ∠AOB=60°, 点P是∠AOB内的定点且( 若点M、N分别是射线OA、OB上异于点O的动点, 则△PMN周长的最小值是 ( )
C. 6 D. 3
14. 平面直角坐标系中的将军饮马问题(初二)
如图, 矩形ABOC的顶点A的坐标为(﹣4, 5), D是OB的中点, E 是OC 上的一点,当△ADE的周长最小时,点E 的坐标是 ( )
C. (0, 2)
15.正方形中的将军饮马问题 (初三)
如图,E,F是正方形ABCD 的边AB的三等分点,P 是对角线AC上的动点,当PE+PF取得最小值时, 的值是 .
16.等边三角形中的将军饮马问题(初二)
如图, 是等边三角形, N 是 AB的中点, AD 是 BC边上的中线, M是 AD上的一个动点, 连接BM, MN, 则 BM+MN的最小值是 .
17. 菱形中的将军饮马问题(初二)
如图, 在菱形ABCD 中, Q为AB的中点, P 为对角线BD上的任意一点,则AP+PQ的最小值为 .
18.平面直角坐标系中造桥选址问题(初二)
如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A,C 分别在 x轴, y轴上, B, D两点坐标分别为B(﹣4, 6), D(0, 4) , 线段EF在边OA上移动,保持EF=3, 当四边形 BDEF 的周长最小时,点E 的坐标为 .
19. 正方形中的将军饮马问题 (初二)
如图, 正方形ABCD 的边长为8, 点M在DC 上且 , N是 AC上的一动点, 则DN+MN 的最小值是 .
20. 正方形中将军饮马综合题(初三)
如图, 正方形 ABCD 中, AB=1, 连接AC, ∠ACD 的角平分线交AD于点E, 在AB上截取 AF=DE, 连接DF, 分别交 CE, CA于点G, H, 点 P 是线段GC上的动点,PQ⊥AC 于点Q, 连接PH. 下列结论: ①CE⊥DF; ②DE+DC=AC; ③EA= AH;④PH+PQ 的最小值是 其中所有正确结论的序号是 .
21菱形中的两点之间线段最短 (初二)
如图, 四边形ABCD是菱形,对角线AC, BD相交于点O, 点P是 AC 上一动点, 点 E 是 AB的中点, 则PD+PE 的最小值为 .
22.等腰三角形中的将军饮马周长最小值问题(初二)
如图, 等腰△ABC 的底边BC=20, 面积为120, 点D在BC边上, 且( 直线EF 是腰AC的垂直平分线,若点M在EF上运动,则 周长的最小值为 .
23.平面直角坐标系中造桥选址问题(初二)
如图, 在平面直角坐标系中,已知A(3, 6), B(﹣2, 2), 在x轴上取两点C,D(点C 在点 D左侧), 且始终保持CD=1, 线段CD在 x轴上平移, 当AD+BC 的值最小时,点C 的坐标为 .
1.解:如图,作点A 关于直线 BC的对称点 A',连接A'O, 其与BC的交点即为点 E, 再作 OF⊥AB交AB于点 F,
∵ A 与 A'关于 BC 对称,
∴ AE=A'E, AE+OE=A'E+OE,
∴ 当且仅当A',O,E三点共线时和最小,如图所示,此时 ,则 A'O 即为所求.
∵正方形ABCD,点O为对角线的交点,
∵A 与A'关于 BC对称, ∴AB=BA'=4,
∴FA'=FB+BA'=2+4=6,
在 Rt△OFA'中, 故选: D.
2. 简解: 过点B作关于 AC的对称点 B', 连接B'E,由对称性质得: AB'=AB=5, EB=EB'
∴FE+EB=FE+EB′, ∴当B′、E、F三点共线且垂直AB时有最小值,如图,B'D 即为所求的最小值,
∵∠C=90° , ∠ABC=75° ∴∠BAC=15°
∴ 在Rt△AB'D中, ∠B'AD=2∠BAC=30°,
故选: B.
3. 解: 如图, 作点B 关于 AC的对称点B', 交AC 于点F, 连接EF, 由对称性可知, PB=PB'
, 当B' 、P、E三点共线时,则B' E的长度即为PE+PB的最小值.
∵四边形ABCD为矩形,
∴AB=CD=4, ∠ABC=90° ,
在 Rt△ABC 中,
∴∠ACB=30° ,
由对称的性质可知, B'B=2BF, B'B⊥AC,
∵BE=BF, ∠CBF=60°, ∴△BEF是等边三角形,
∴BE=BF=B'F, ∴△BEB'是直角三角形,
∴PE+PB 的最小值为6, 故答案为: 6.
4. 解: 作 B 点关于 EC 的对称点F, BF 交 EC于点 H,过F 点作 FG⊥BC 交 BC 的延长线于点G, 连接PF.
由对称性质得: BP=FP, ∴AP+BP=AP+PF,
当A、P、F三点共线时, AF 即为AP+BP的最小值,
∵E 点是 AD的中点, 正方形ABCD的边长为5,
∵BH⊥EC, ∴∠BHC=90° ,
∴BH=2HC, 在 Rt△BCH中, ( 设HC=a, 则 BH=2a, 且已知BC=5,
在 Rt△BGF中,同理可得, BG=2FG, ∴GF=4, BG=8,过点 F 作 FM⊥AB交于 M,
依题意得: MF=BG=8, AM=1,
在 Rt△AFM 中,
∴AP+BP的最小值为 故答案为:
5.解:作点 E 关于 DC的对称点 E', 设AB 的中点为点 O,连接OE', 交 DC于点 P, 连接PE, 如图:
∵动点M在边长为2的正方形ABCD 内, 且AM⊥BM,
∴点 M在以AB 为直径的半圆上,
∵正方形 ABCD的边长为2,
∴AD=AB=2, ∠DAB=90° ,
∵E是AD的中点,
∵作点 E 关于 DC 的对称点 E',
∴DE'=DE=1, PE=PE', ∴AE'=AD+DE'=2+1=3,
∴ PE+PM=PE'+PM, 连接OE', 于 CD 交于P, 与半圆交于点 M, 此时E'M 的值, 即为PE+PM的最小值.在 Rt△AOE'中, 故选: A.
6. 简解: 如图, 作 BDCE, 则EC=BD.
∴ AC+BD=AC+EC,根据将军饮马原理,过点A作x 轴的对称点 A′, 则AC=A′C.
∴ AC+BD=AC+EC=A'C+EC,
当E、C、A'三点共线时,有最小值, 即为所求, ∴AC+BD的最小值为 故选: B.
7. 解: 过点P作EF∥AB, 分别交AD, BC于点E, F,
∵四边形ABCD是正方形,
∴四边形ABFE和四边形EFCD 都是矩形,
正方形ABCD, 正方形ABCD的边长为4,
解得FB=2,
∴CF=BC-FB=4-2=2=FB,
即 F 是 BC的中点, 且P 点在线段EF 上运动.
作点 M关于 CD的对称点 M' , 连接M' G,
则M' G=MG, M' C=MC=1,
∴MG+GP=M' G+GP≥M' F,
∴MG+GP的最小值为M' F 的长,
∵M' F=M' C+CF=1+2=3,
∴MG+GP的最小值为3, 故答案为: 3.
8. 解: ∵在Rt△ABO中, ∠OBA=90°, A(4, 4), 点D为OB的中点, ∴BC=3, OD=BD=2, ∴D(2, 0), C(4,3),作D关于直线OA的对称点E,连接EC交OA于P,则此时, 四边形PDBC周长最小, E(0,2),
∵直线OA 的解析式为y=x,设直线EC的解析式为 解得:
∴直线EC的解析式为 解 得, 故选: C.
9. 解: 如图, 作点F关于 BC的对称点 M, 连接FM交BC于点N, 连接EM, 交BC于点 H
∵点E, F将对角线AC三等分, 且AC=12,
∴EC=8, FC=4=AE,
∵点M 与点 F 关于 BC对称
∴CF=CM=4, ∠ACB=∠BCM=45° ∴∠ACM=90°
则在线段BC存在点H到点E和点F的距离之和最小为 ,在点 H右侧,当点 P 与点 C 重合时, 则PE+PF=12
∴点 P 在 CH上时, 在点H左侧,当点 P 与点 B重合时,
∵AB=BC, AE=CF, ∠BAE=∠BCF,
∴△ABE≌△CBF(SAS)∴BE=BF=2 ,
∴点 P 在 BH 上时,
∴在线段BC上点H的左右两边各有一个点P,使得PE+PF=9, 同理在线段AB, AD, CD上都存在两个点P, 使得PE+PF=9. 即共有8个点 P 满足PE+PF=9, 故选: D.
10. 简解: 如图, 在 BA 上截取BE=BC, 连接ME,∵∠ABC的平分线交AC于点 D, ∴∠EBM=∠NBM,在△BME与△BMC中, △BME≌△BMC(SAS),∴ME=MC. ∴CM+MN=CM+ME.
当N、M、E三点共线且垂直BC时,取最小值,EF即为所求最小值: 故选: C.
11. 解: 如图, 作点E关于AC的对称点 E' , 过点 E'作 E' F⊥AB 于点 F, 则E' F 即为所求最小值,∵四边形ABCD 是菱形, ∴点E' 在 CD 上, 由 得: 解得: E' F 即 PE+PM的最小值是 故选: C.
12. 解: 连接OE, 过点O作OF⊥AB, 垂足为F, 并延长到点 O' , 使O' F=OF, 连接O' E交直线AB 于点P,连接OP, ∴AP 是OO'的垂直平分线, ∴OP=O' P,∴OP+PE=O'P+PE, 当O' 、P、E三点共线时, O' E即为OP+PE的值最小,
∵四边形ABCD 是菱形, ∴AD=AB=3, OA=OC=
∵∠BAD=60°, ∴△ADB是等边三角形,
∵CE⊥AH, ∴∠AEC=90° ,
∵AE平分∠CAB, ∴∠OAE=∠EAB,
∴∠OEA=∠EAB, ∴OE∥AB,
∴∠EOF=∠AFO=90°,
在 Rt△AOF 中,
在 Rt△EOO' 中,
∴OP+PE的最小值为 故答案为:
13. 解: 作P 点分别关于OA、OB的对称点 C、D, 连接CD分别交OA、 OB于M、N, 则MP=MC, NP=ND,OP=OD=OC= ,∠BOP=∠BOD,∠AOP=∠AOC,∴PN+PM+MN=ND+MN+MC=DC, ∠COD=∠BOP+∠BOD+∠AOP+∠AOC=2∠AOB=120°,
∴此时△PMN周长最小, 作 OH⊥CD 于H, 则CH=DH,
故选: D.
14. 解:如图, 作A关于y轴的对称点A', 连接A'D交y轴于E, 则此时, △ADE的周长最小,
∵四边形 ABOC 是矩形,
∴AC∥OB, AC=OB, ∵A点的坐标为(-4, 5) ,
∴A′ (4,5), B(-4,0), ∵D是OB的中点, ∴D(-2, 0),设直线DA'的解析式为
∴直线DA'的解析式为 当x=0时, 故选: B .
15. 解: 作点 E 关于 AC 的对称点 E', 连接 FE'交 AC于点 P', 连接PE',
∴PE=PE', ∴PE+PF=PE'+PF≥E'F,故当PE+PF 取得最小值时, 点 P 位于点 P'处,
∴当PE+PF取得最小值时, 求 的值,只要求出 的值即可.
∵正方形ABCD 是关于 AC 所在直线轴对称,
∴点 E 关于 AC 所在直线对称的对称点 E'在 AD 上,且 AE'=AE, 过点F 作FG⊥AB 交AC 于点G,则∠GFA=90° ,
∵四边形 ABCD 是正方形,
∴∠DAB=∠B=90°, ∠CAB=∠ACB=45° ,
∴FG∥BC∥AD, ∠AGF=∠ACB=45° , ∴GF=AF,
∵E, F是正方形ABCD的边AB的三等分点,
又∵FG∥
故答案为: .
16.解: 如下图, 连接CM, CN,
∵△ABC是等边三角形, AD 是中线, ∴AD⊥BC, BD=CD, ∴AD是BC的垂直平分线, ∴BM=CM, ∴BM+MN=CM+MN, 即当点C、M、N三点共线时,BM+MN最小值为CN的长,
∵点 N 是 AB 的中点,
最小值为: 故答案为:
17. 解: 如图, 连接 PC, AC, CQ. ∵四边形ABCD 是菱形, ∴∠ABP=∠PBC, 在△ABP和△CBP中,△ABP≌△CBP (SAS) , ∴PA=PC,
∵AB∥CD, ∴∠ABC+∠BCD=180°,
∴∠ABC=180° -120° =60°, ∵AB=BC,
∴△ABC是等边三角形, ∵AQ=QB, ∴CQ⊥AB,
的最小值为
故答案为:
18. 解: 在 BC上截取BH=3, 作点 D 关于x轴的对称点G, 连接GH交AO于点E, ∴BH=EF=3, BC∥AO, ∴四边形BHEF是平行四边形,
∴BF=EH,∵点D与点G关于x轴对称,
∴DE=GE, 点 G坐标为 (0, -4),
∵四边形BDEF的周长=EF+BF+BD+DE,
∴四边形BDEF的周长=EF+EH+EG+BD,
∵EF和BD 是定值, ∴当EH+GE有最小值时, 四边形BDEF的周长有最小值, ∴当点E, 点H, 点 G 共线时,EH+GE有最小值, ∵点B(-4, 6) , ∴点H(-1, 6),设直线GH的解析式为y=kx+b, 把点G(0, -4) 、点H(--1,6)代入,待定系数法可得,直线 GH 的解析式为:y=-10x-4, ∴当y=0时, ∴点 故答案为:
19.解:∵正方形是轴对称图形,点 B 与点 D 是关于直线AC为对称轴的对称点, ∴连接BN, BD, ∴BN=ND,∴DN+MN=BN+MN, 连接BM交AC于点 P,
∵点 N为AC上的动点,由三角形两边和大于第三边可知, 当点N运动到点 P时, BN+MN=BP+PM=BM,BN+MN的最小值为BM的长度,
∵四边形ABCD 为正方形,
∴BC=CD=8, CM=8-2=6, ∠BCM=90° ,
∴BM=10, ∴DN+MN的最小值是10. 故答案为: 10.
20. 解:∵正方形ABCD, ∴CD=AD,∠CDE=∠DAF=90° , ∴∠ADF+∠CDF=90° ,在△CDE和△DAF中, 易证△CDE≌△DAF(ASA) ,
∴∠DCE=∠ADF, ∴∠DCE+∠CDF=90°,
∴∠DGC=90°, ∴CE⊥DF, 故①正确;
∵CE平分∠ACD, ∴∠DCE=∠HCG, 在△GCD和△GCH中, 易证∴△GCD≌△GCH(ASA) ,
∴CD=CH, ∠CDH=∠CHD,
∵正方形ABCD, ∴CD∥AB, ∴∠CDF=∠AFD,
∴∠CHD=∠AFD, ∵∠CHD=∠AHF,
∴∠AFD=∠AHF, ∴AF=AH,
∴AC=AH+CH=AF+CD=DE+CD, 故②正确,设DE=AF=AH=a,
∵∠AHF=∠DHC, ∠CDF=∠AFH,
- 故③错误;
∵△GCD≌△GCH, ∴DG=GH,
∵CE⊥DF, ∴CG垂直平分DH, ∴DP=PH,当DQ⊥HC时, PH+PQ=DP+PQ有最小值,过点 D作DM⊥HC,则DM的长度为PH+PQ的最小值,
故④正确. 故答案为: ①②④.
21. 解: 如图, 连接DE, ∵四边形ABCD 是菱形, 对角线AC, BD 相交于点 O,
即△ABD
是等边三角形,又∵E 是 AB 的中点,
∵DP+PE≥DE, ∴PD+PE 的最小值为 DE 的长, 即PD+PE的最小值为: 故答案为:
22. 解: 如图, 作AH⊥BC于 H, 连接AM,
∵EF 垂直平分线段AC, ∴MA=MC, ∴DM+MC=AM+MD, ∴当A、D、M共线时, DM+MC的值最小,
∵等腰△ABC的底边BC=20, 面积为120, AH⊥BC,
∴BH=CH=10, AH=12, ∴DH=CH--CD=5,
∴AD=13, ∴DM+MC的最小值为13,
∴△CDM周长的最小值=13+5=18, 故答案为18.
23. 解: 把A(3, 6) 向左平移1得A' (2, 6) , 作点B 关于x轴的对称点B' , 连接B' A' 交x轴于 C, 在x轴上取点 D(点C在点 D左侧) , 使CD=1, 连接AD,则AD+BC的值最小,∵B(-2,2), ∴B′ (-2, -2),由A' (2, 6) 、B' (-2, -2)的坐标, 得直线 B' A'的解析式为y=2x+2,当y=0时,x=-1,∴C(-1,0),故答案为: (-1, 0) .
24. 解: 如图, 作点 D关于 OB的对称点 D', 连接D'C交 OB于点 E', 连接E' D、OD' ,
此时E' C+E' D 最小, 即: E' C+E' D=CD' , 由题意得, ∠COD=∠DOB=∠BOD′ =30° , ∴∠COD′ =
CD弧的长 ∴阴影部分周长的最小值为 故答案为:
同课章节目录
