2024年中考数学复习位置的确定、函数及图象专项练习(含答案)
文档属性
| 名称 | 2024年中考数学复习位置的确定、函数及图象专项练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 629.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-12 11:17:08 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
位置的确定、函数及图象专项练习
A基础训练
1.在平面直角坐标系中,将点 A(--2,3)向右平移4个单位长度,得到的对应点A'的坐标为 ( )
A.(2,7) B.(-6,3)
C.(2,3) D.(-2,-1)
2.在平面直角坐标系中,将点(2,1)向下平移3个单位长度,所得点的坐标是( )
A.(--1,1) C.(2,4) B.(5,1)D.(2,-2)
3.在平面直角坐标系中,将点 P(--3,2)向右平移3个单位得到点 P',则点 P'关于 x轴的对称点的坐标为( )
A.(0,—2) B.(0,2)
C.(-6,2) D.(-6,-2)
4.在平面直角坐标系中,点 P(x +2,-3)所在的象限为 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
5.小李、小王、小张、小谢原有位置如图(横为排、竖为列),小李在第2 排第4列,小王在第3 排第3 列,小张在第 4 排第 2 列,小谢在第5 排第4 列.撤走第一排,仍按照原有确定位置的方法确定新的位置,下列说法正确的是( )
A.小李现在位置为第1 排第2列
B.小张现在位置为第 3 排第2 列
C.小王现在位置为第 2 排第2 列
D.小谢现在位置为第 4 排第2 列
6.函数 的自变量的取值范围是 ( )
A.x≥--1 B.x≥-1且x≠0
C. x>0 D. x>-1且x≠0
7.如图,∠BOA=∠B=30°,OA=2,将△AOB 绕点O 逆时针旋转90°,点 B 的对应点 B'的坐标是 ( )
B.(-3, )
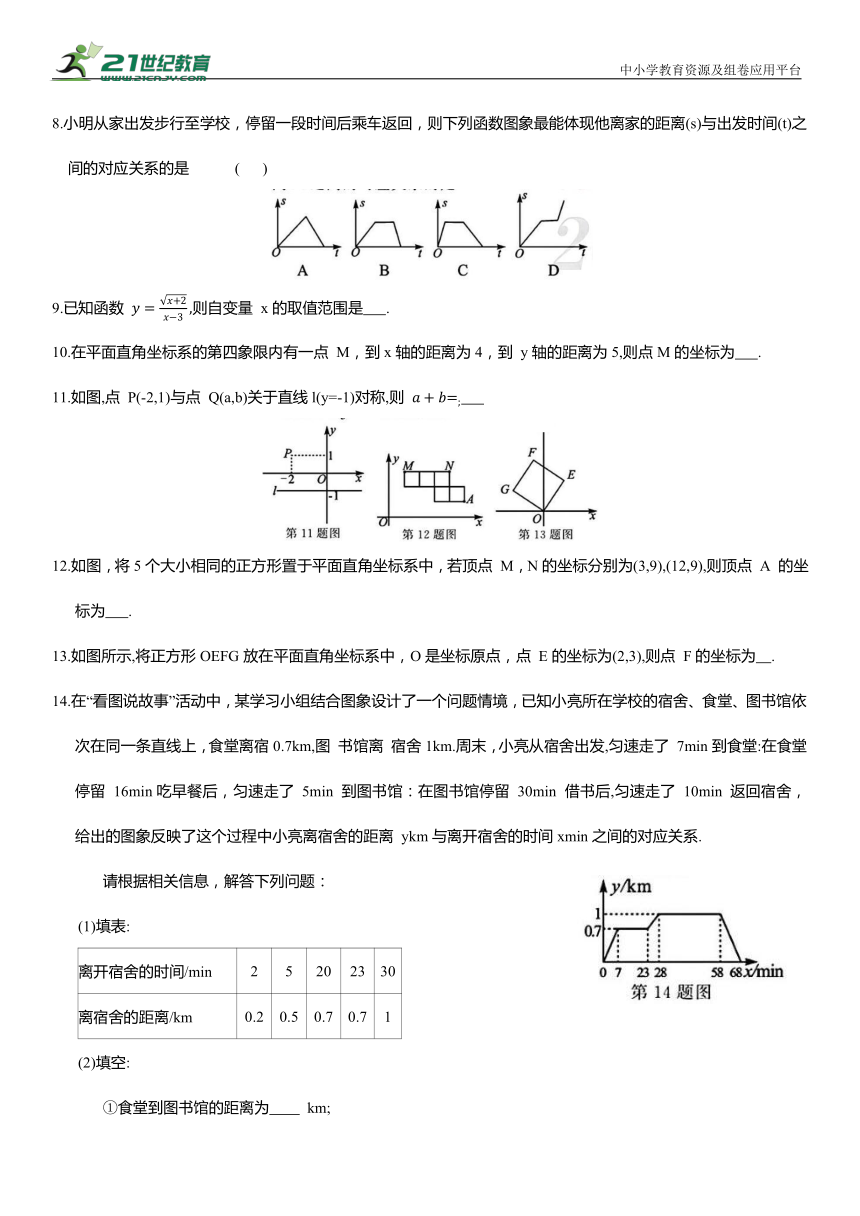
8.小明从家出发步行至学校,停留一段时间后乘车返回,则下列函数图象最能体现他离家的距离(s)与出发时间(t)之间的对应关系的是 ( )
9.已知函数 则自变量 x的取值范围是 .
10.在平面直角坐标系的第四象限内有一点 M,到x轴的距离为4,到 y轴的距离为5,则点M的坐标为 .
11.如图,点 P(-2,1)与点 Q(a,b)关于直线l(y=-1)对称,则
12.如图,将5个大小相同的正方形置于平面直角坐标系中,若顶点 M,N的坐标分别为(3,9),(12,9),则顶点 A 的坐标为 .
13.如图所示,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点 E的坐标为(2,3),则点 F的坐标为 .
14.在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境,已知小亮所在学校的宿舍、食堂、图书馆依次在同一条直线上,食堂离宿0.7km,图 书馆离 宿舍1km.周末,小亮从宿舍出发,匀速走了 7min到食堂:在食堂停留 16min吃早餐后,匀速走了 5min 到图书馆:在图书馆停留 30min 借书后,匀速走了 10min 返回宿舍,给出的图象反映了这个过程中小亮离宿舍的距离 ykm与离开宿舍的时间xmin之间的对应关系.
请根据相关信息,解答下列问题:
(1)填表:
离开宿舍的时间/min 2 5 20 23 30
离宿舍的距离/km 0.2 0.5 0.7 0.7 1
(2)填空:
①食堂到图书馆的距离为 km;
②小亮从食堂到图书馆的速度为 km/min;
③小亮从图书馆返回宿舍的速度为 km/min;
④当小亮离宿舍的距离为0.6km 时,他离开宿舍的时间为 min.
(3)当0≤x≤28时,请直接写出y关于x 的函数解析式.
B 能力提升
15.新龟兔赛跑的故事:龟兔从同一地点同时出发后,兔子很快把乌龟远远甩在后头.骄傲自满的兔子觉得自已遥遥领先,就躺在路边呼呼大睡起来.当它一觉醒来,发现乌龟已经超过它,于是奋力直追,最后同时到达终点.用s ,s 分别表示乌龟和兔子赛跑的路程,t为赛跑时间,则下列图象中与故事情节相吻合的是( )
16.如图,在平面直角坐标系中.Rt△OAB的斜边OA 在第一象限,并与x轴的正半轴夹角为30°,C为OA 的中点,BC=1,则点 A的坐标为 ( )
B.( ,1)
C.(2,1)
D.(2, )
17.如图,在矩形ABCD中,AB=3,BC=4,动点 P 沿折线BCD 从点 B 开始运动到点 D,设点 P 运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是 ( )
18.如图,在四边形 ABCD中,AD∥BC,∠D=90°,AB=4,BC=6,∠BAD=30°.动点 P 沿路径A→B→C→D从点A 出发,以每秒1个单位长度的速度向点 D 运动.过点P 作PH⊥AD,垂足为 H.设点 P 运动的时间为x(单位:s),△APH的面积为y,则y关于x的函数图象大致是( )
19.A,B两地相距240km,甲货车从 A 地以40km/h的速度匀速前往 B 地,到达B 地后停止,在甲出发的同时,乙货车从 B 地沿同一公路匀速前往 A 地,到达 A 地后停止,两车之间的路程y(km)与甲货车出发时间x(h)之间的函数关系如图中的折线CD-DE--EF所示.其中点C的坐标是(0,240),点 D 的坐标是(2.4,0),则点 E 的坐标是 .
核心 素养专练
20.若定义一种新运算:a b 例如:3 1=3-1=2;5 4=5+4-6=3.则函数y=(x+2) (x-1)的图象大致是 ( )
21.如图①,正方形ABCD中,AC,BD 相交于点O,E是OD 的中点,动点 P从点E 出发,沿着 E→O→B→A的路径以每秒1个单位长度的速度运动到点 A.在此过程中线段AP 的长度y 随着运动时间x 的函数关系如图②所示,则AB的长为( )
B.4 C.3 D.2
22.如图,在△ABC中,∠ACB=90°,边 BC在x 轴上,顶点 A,B的坐标分别为(-2,6)和(7,0).将正方形OCDE 沿x 轴向右平移,当点 E 落在AB 边上时,点 D 的坐标为 ( )
B.(2,2)
D.(4,2)
1-8CDADBBAB
x≥-2且x≠3
(5,-4)
-5
(15,3)
(-1,5)
14.0.3 0.06 0.1 6或62
解:当0≤x≤7时,y=0.1x;
当7当 2315-18CBDD
(4,160)
20-22 AAB
位置的确定、函数及图象专项练习
A基础训练
1.在平面直角坐标系中,将点 A(--2,3)向右平移4个单位长度,得到的对应点A'的坐标为 ( )
A.(2,7) B.(-6,3)
C.(2,3) D.(-2,-1)
2.在平面直角坐标系中,将点(2,1)向下平移3个单位长度,所得点的坐标是( )
A.(--1,1) C.(2,4) B.(5,1)D.(2,-2)
3.在平面直角坐标系中,将点 P(--3,2)向右平移3个单位得到点 P',则点 P'关于 x轴的对称点的坐标为( )
A.(0,—2) B.(0,2)
C.(-6,2) D.(-6,-2)
4.在平面直角坐标系中,点 P(x +2,-3)所在的象限为 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
5.小李、小王、小张、小谢原有位置如图(横为排、竖为列),小李在第2 排第4列,小王在第3 排第3 列,小张在第 4 排第 2 列,小谢在第5 排第4 列.撤走第一排,仍按照原有确定位置的方法确定新的位置,下列说法正确的是( )
A.小李现在位置为第1 排第2列
B.小张现在位置为第 3 排第2 列
C.小王现在位置为第 2 排第2 列
D.小谢现在位置为第 4 排第2 列
6.函数 的自变量的取值范围是 ( )
A.x≥--1 B.x≥-1且x≠0
C. x>0 D. x>-1且x≠0
7.如图,∠BOA=∠B=30°,OA=2,将△AOB 绕点O 逆时针旋转90°,点 B 的对应点 B'的坐标是 ( )
B.(-3, )
8.小明从家出发步行至学校,停留一段时间后乘车返回,则下列函数图象最能体现他离家的距离(s)与出发时间(t)之间的对应关系的是 ( )
9.已知函数 则自变量 x的取值范围是 .
10.在平面直角坐标系的第四象限内有一点 M,到x轴的距离为4,到 y轴的距离为5,则点M的坐标为 .
11.如图,点 P(-2,1)与点 Q(a,b)关于直线l(y=-1)对称,则
12.如图,将5个大小相同的正方形置于平面直角坐标系中,若顶点 M,N的坐标分别为(3,9),(12,9),则顶点 A 的坐标为 .
13.如图所示,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点 E的坐标为(2,3),则点 F的坐标为 .
14.在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境,已知小亮所在学校的宿舍、食堂、图书馆依次在同一条直线上,食堂离宿0.7km,图 书馆离 宿舍1km.周末,小亮从宿舍出发,匀速走了 7min到食堂:在食堂停留 16min吃早餐后,匀速走了 5min 到图书馆:在图书馆停留 30min 借书后,匀速走了 10min 返回宿舍,给出的图象反映了这个过程中小亮离宿舍的距离 ykm与离开宿舍的时间xmin之间的对应关系.
请根据相关信息,解答下列问题:
(1)填表:
离开宿舍的时间/min 2 5 20 23 30
离宿舍的距离/km 0.2 0.5 0.7 0.7 1
(2)填空:
①食堂到图书馆的距离为 km;
②小亮从食堂到图书馆的速度为 km/min;
③小亮从图书馆返回宿舍的速度为 km/min;
④当小亮离宿舍的距离为0.6km 时,他离开宿舍的时间为 min.
(3)当0≤x≤28时,请直接写出y关于x 的函数解析式.
B 能力提升
15.新龟兔赛跑的故事:龟兔从同一地点同时出发后,兔子很快把乌龟远远甩在后头.骄傲自满的兔子觉得自已遥遥领先,就躺在路边呼呼大睡起来.当它一觉醒来,发现乌龟已经超过它,于是奋力直追,最后同时到达终点.用s ,s 分别表示乌龟和兔子赛跑的路程,t为赛跑时间,则下列图象中与故事情节相吻合的是( )
16.如图,在平面直角坐标系中.Rt△OAB的斜边OA 在第一象限,并与x轴的正半轴夹角为30°,C为OA 的中点,BC=1,则点 A的坐标为 ( )
B.( ,1)
C.(2,1)
D.(2, )
17.如图,在矩形ABCD中,AB=3,BC=4,动点 P 沿折线BCD 从点 B 开始运动到点 D,设点 P 运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是 ( )
18.如图,在四边形 ABCD中,AD∥BC,∠D=90°,AB=4,BC=6,∠BAD=30°.动点 P 沿路径A→B→C→D从点A 出发,以每秒1个单位长度的速度向点 D 运动.过点P 作PH⊥AD,垂足为 H.设点 P 运动的时间为x(单位:s),△APH的面积为y,则y关于x的函数图象大致是( )
19.A,B两地相距240km,甲货车从 A 地以40km/h的速度匀速前往 B 地,到达B 地后停止,在甲出发的同时,乙货车从 B 地沿同一公路匀速前往 A 地,到达 A 地后停止,两车之间的路程y(km)与甲货车出发时间x(h)之间的函数关系如图中的折线CD-DE--EF所示.其中点C的坐标是(0,240),点 D 的坐标是(2.4,0),则点 E 的坐标是 .
核心 素养专练
20.若定义一种新运算:a b 例如:3 1=3-1=2;5 4=5+4-6=3.则函数y=(x+2) (x-1)的图象大致是 ( )
21.如图①,正方形ABCD中,AC,BD 相交于点O,E是OD 的中点,动点 P从点E 出发,沿着 E→O→B→A的路径以每秒1个单位长度的速度运动到点 A.在此过程中线段AP 的长度y 随着运动时间x 的函数关系如图②所示,则AB的长为( )
B.4 C.3 D.2
22.如图,在△ABC中,∠ACB=90°,边 BC在x 轴上,顶点 A,B的坐标分别为(-2,6)和(7,0).将正方形OCDE 沿x 轴向右平移,当点 E 落在AB 边上时,点 D 的坐标为 ( )
B.(2,2)
D.(4,2)
1-8CDADBBAB
x≥-2且x≠3
(5,-4)
-5
(15,3)
(-1,5)
14.0.3 0.06 0.1 6或62
解:当0≤x≤7时,y=0.1x;
当7
(4,160)
20-22 AAB
同课章节目录
