2024年中考数学复习--反比例函数的综合题
文档属性
| 名称 | 2024年中考数学复习--反比例函数的综合题 |
|
|
| 格式 | docx | ||
| 文件大小 | 427.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-12 00:00:00 | ||
图片预览



文档简介
反比例函数的综合题
A 基础 训练
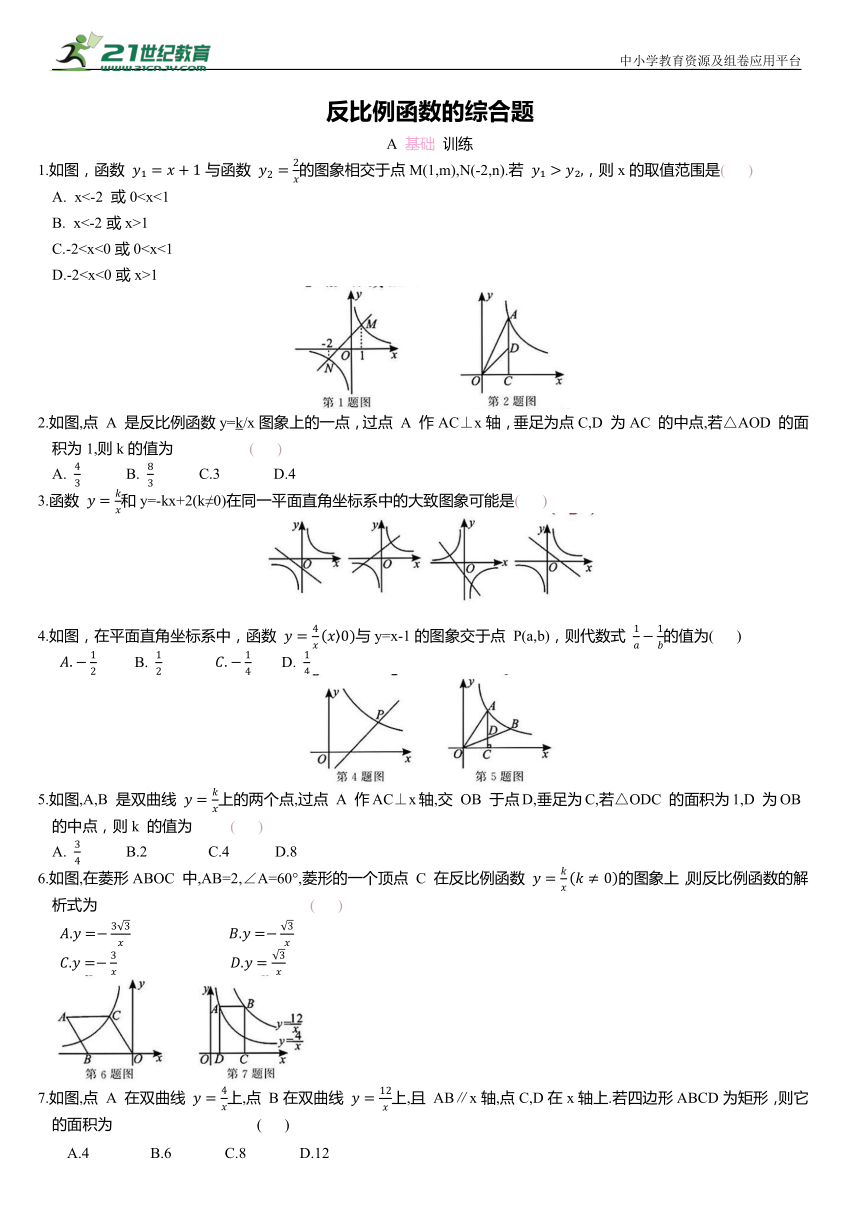
1.如图,函数 与函数 的图象相交于点M(1,m),N(-2,n).若 ,则x的取值范围是( )
A. x<-2 或0B. x<-2或x>1
C.-2D.-21
2.如图,点 A 是反比例函数y=k/x图象上的一点,过点 A 作AC⊥x轴,垂足为点C,D 为AC 的中点,若△AOD 的面积为1,则k的值为 ( )
A. B. C.3 D.4
3.函数 和y=-kx+2(k≠0)在同一平面直角坐标系中的大致图象可能是( )
4.如图,在平面直角坐标系中,函数 与y=x-1的图象交于点 P(a,b),则代数式 的值为( )
B. D.
5.如图,A,B 是双曲线 上的两个点,过点 A 作AC⊥x轴,交 OB 于点D,垂足为C,若△ODC 的面积为1,D 为OB 的中点,则k 的值为 ( )
A. B.2 C.4 D.8
6.如图,在菱形ABOC 中,AB=2,∠A=60°,菱形的一个顶点 C 在反比例函数 的图象上,则反比例函数的解析式为 ( )
7.如图,点 A 在双曲线 上,点 B在双曲线 上,且 AB∥x轴,点C,D在x轴上.若四边形ABCD为矩形,则它的面积为 ( )
A.4 B.6 C.8 D.12
8.如图,点 A 是反比例函数 图象上的一点,AB垂直于x 轴,垂足为 B,△OAB的面积为 6.若点P(a,7)也在此函数的图象上,则 ______
9.在平面直角坐标系xOy中,已知直线y=mx(m>0)与双曲线 交于A,C两点(点A 在第一象限),直线 y=nx(n<0)与双曲线 交于B,D 两点.当这两条直线互相垂直,且四边形 ABCD 的周长为10 时,点 A 的坐标为___
10.如图,一次函数y=x+5的图象与反比例函数 k为常数且k≠0)的图象相交于A(-1,m),B两点.
(1)求反比例函数的解析式;
(2)将一次函数y=x+5的图象沿 y 轴向下平移b个单位(b>0),使平移后的图象与反比例函数 y 的图象有且只有一个交点,求b的值.
B 能力提升
11如图,在平面直角坐标系中,直线y=-x与双曲线. 交于A,B两点,P是以点C(2,2)为圆心,半径长为1的圆上一动点,连接AP,Q为AP 的中点.若线段OQ长度的最大值为2,则k的值为( )
C. -2
12.)如图,在平面直角坐标系中,矩形ABCD的对角线AC 的中点与坐标原点重合,点 E 是x 轴上一点,连接AE.若 AD 平分∠OAE,反比例函数 >0,x>0)的图象经过AE上的两点A,F,且AF=EF,△ABE的面积为18,则k的值为
( )
A.6 B.12 C.18 D.24
13.如图,菱形ABCD 顶点 A 在函数 的图象上,函数 3,x>0)的图象关于直线 AC对称,且经过 B,D两点,若AB=2,∠BAD=30°,则k=
14.如图,反比例函数 0)的图象与正比例函数y=2x的图象相交于A(1,a),B两点,点C在第四象限,BC∥x轴;
(1)求k 的值;
(2)以 AB,BC 为边作菱形ABCD,求 D点坐标.
核心素养专练
15.模具厂计划生产面积为4,周长为m的矩形模具,对于m的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下:
(1)建立函数模型
设矩形相邻两边的长分别为x,y,由矩形的面积为4,得xy=4,即 由周长为m,得2(x+y)=m,即 满足要求的(x,y)应是两个函数图象在第 一 象限内交点的坐标.
(2)画出函数图象
函数 的图象如图所示,而函数 的图象可由直线y=--x平移得到,请在同一直角坐标系中直接画出直线y=-x;
(3)平移直线y=-x,观察函数图象
①当直线平移到与函数 的图象有唯一交点(2,2)时,周长m 的值为 ;
②在直线平移过程中,交点个数还有哪些情况 请写出交点个数及对应的周长 m的取值范围;
(4)得出结论
若能生产出面积为4的矩形模具,则周长m的取值范围为
1-7DDDCDBC
,2 )或(2 , )
10.解:(1)由题意,将点 A(-1,m)代入一次函数 y=x+5,得m=-1+5=4,
∴A(-1,4).将点 A(-1,4)代入 得 =4,解得k=-4.
则反比例函数的解析式为
(2)将一次函数 y=x+5 的图象沿 y轴向下平移b个单位得到的一次函数的解析式为 y=x+5-b.联立 整理得 0.
∵一次函数 y=x+5-b的图象与反比例函数 的图象有且只有一个交点,
∴关于x的一元二次方程 只有一个实数根.
∴此方程的根的判别式 0,
解得 ,则b的值为1或9.
11-12AB
13.6+
14.解:(1)根据题意,点 A(1,a)在正比例函数 y=2x 上,故将点 A(1,a)代入正比例函数 y=2x中,得a=2,故点 A 的坐标为(1,2),点 A又在反比例函数图象上,将A(1,2)代入反比例函数解析式中,得k=2.
(2)A,B为反比例函数与正比例函数的交点,故可得 解得 已知点 A 坐标为(1,2),故点 B 坐标为(﹣1,﹣2),根据两点间距离公式可得 根据已知条件中四边形 ABCD 为菱形,故 AB=AD=2 . AD∥BC∥x轴,则点 D 坐标为(1+2 ,2).
15.解:(1)一 [x,y都是边长,因此,都是正数,故点(x,y)在第一象限.]
(2)图象如图所示.
(3)①8 [把点(2,2)代人 得 解得m=8.]
②在直线平移过程中,交点个数有:0个,1个,2个三种情况.0个交点时,m<8;1个交点时,m=8;2个交点时,m>8.
中小学教育资源及组卷应用平台
(4)m≥8[联立 和 整理,得 时,两个函数有交点,解得 m≥8.]
1-7DDDCDBC
,2 )或(2 , )
10.解:(1)由题意,将点 A(-1,m)代入一次函数 y=x+5,得m=-1+5=4,
∴A(-1,4).将点 A(-1,4)代入 得 =4,解得k=-4.
则反比例函数的解析式为
(2)将一次函数 y=x+5 的图象沿 y轴向下平移b个单位得到的一次函数的解析式为 y=x+5-b.联立 整理得 0.
∵一次函数 y=x+5-b的图象与反比例函数 的图象有且只有一个交点,
∴关于x的一元二次方程 只有一个实数根.
∴此方程的根的判别式 0,
解得 ,则b的值为1或9.
11-12AB
13.6+
14.解:(1)根据题意,点 A(1,a)在正比例函数 y=2x 上,故将点 A(1,a)代入正比例函数 y=2x中,得a=2,故点 A 的坐标为(1,2),点 A又在反比例函数图象上,将A(1,2)代入反比例函数解析式中,得k=2.
(2)A,B为反比例函数与正比例函数的交点,故可得 解得 已知点 A 坐标为(1,2),故点 B 坐标为(﹣1,﹣2),根据两点间距离公式可得 根据已知条件中四边形 ABCD 为菱形,故 AB=AD=2 . AD∥BC∥x轴,则点 D 坐标为(1+2 ,2).
15.解:(1)一 [x,y都是边长,因此,都是正数,故点(x,y)在第一象限.]
(2)图象如图所示.
(3)①8 [把点(2,2)代人 得 解得m=8.]
②在直线平移过程中,交点个数有:0个,1个,2个三种情况.0个交点时,m<8;1个交点时,m=8;2个交点时,m>8.
(4)m≥8[联立 和 整理,得 时,两个函数有交点,解得 m≥8.]
A 基础 训练
1.如图,函数 与函数 的图象相交于点M(1,m),N(-2,n).若 ,则x的取值范围是( )
A. x<-2 或0
C.-2
2.如图,点 A 是反比例函数y=k/x图象上的一点,过点 A 作AC⊥x轴,垂足为点C,D 为AC 的中点,若△AOD 的面积为1,则k的值为 ( )
A. B. C.3 D.4
3.函数 和y=-kx+2(k≠0)在同一平面直角坐标系中的大致图象可能是( )
4.如图,在平面直角坐标系中,函数 与y=x-1的图象交于点 P(a,b),则代数式 的值为( )
B. D.
5.如图,A,B 是双曲线 上的两个点,过点 A 作AC⊥x轴,交 OB 于点D,垂足为C,若△ODC 的面积为1,D 为OB 的中点,则k 的值为 ( )
A. B.2 C.4 D.8
6.如图,在菱形ABOC 中,AB=2,∠A=60°,菱形的一个顶点 C 在反比例函数 的图象上,则反比例函数的解析式为 ( )
7.如图,点 A 在双曲线 上,点 B在双曲线 上,且 AB∥x轴,点C,D在x轴上.若四边形ABCD为矩形,则它的面积为 ( )
A.4 B.6 C.8 D.12
8.如图,点 A 是反比例函数 图象上的一点,AB垂直于x 轴,垂足为 B,△OAB的面积为 6.若点P(a,7)也在此函数的图象上,则 ______
9.在平面直角坐标系xOy中,已知直线y=mx(m>0)与双曲线 交于A,C两点(点A 在第一象限),直线 y=nx(n<0)与双曲线 交于B,D 两点.当这两条直线互相垂直,且四边形 ABCD 的周长为10 时,点 A 的坐标为___
10.如图,一次函数y=x+5的图象与反比例函数 k为常数且k≠0)的图象相交于A(-1,m),B两点.
(1)求反比例函数的解析式;
(2)将一次函数y=x+5的图象沿 y 轴向下平移b个单位(b>0),使平移后的图象与反比例函数 y 的图象有且只有一个交点,求b的值.
B 能力提升
11如图,在平面直角坐标系中,直线y=-x与双曲线. 交于A,B两点,P是以点C(2,2)为圆心,半径长为1的圆上一动点,连接AP,Q为AP 的中点.若线段OQ长度的最大值为2,则k的值为( )
C. -2
12.)如图,在平面直角坐标系中,矩形ABCD的对角线AC 的中点与坐标原点重合,点 E 是x 轴上一点,连接AE.若 AD 平分∠OAE,反比例函数 >0,x>0)的图象经过AE上的两点A,F,且AF=EF,△ABE的面积为18,则k的值为
( )
A.6 B.12 C.18 D.24
13.如图,菱形ABCD 顶点 A 在函数 的图象上,函数 3,x>0)的图象关于直线 AC对称,且经过 B,D两点,若AB=2,∠BAD=30°,则k=
14.如图,反比例函数 0)的图象与正比例函数y=2x的图象相交于A(1,a),B两点,点C在第四象限,BC∥x轴;
(1)求k 的值;
(2)以 AB,BC 为边作菱形ABCD,求 D点坐标.
核心素养专练
15.模具厂计划生产面积为4,周长为m的矩形模具,对于m的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下:
(1)建立函数模型
设矩形相邻两边的长分别为x,y,由矩形的面积为4,得xy=4,即 由周长为m,得2(x+y)=m,即 满足要求的(x,y)应是两个函数图象在第 一 象限内交点的坐标.
(2)画出函数图象
函数 的图象如图所示,而函数 的图象可由直线y=--x平移得到,请在同一直角坐标系中直接画出直线y=-x;
(3)平移直线y=-x,观察函数图象
①当直线平移到与函数 的图象有唯一交点(2,2)时,周长m 的值为 ;
②在直线平移过程中,交点个数还有哪些情况 请写出交点个数及对应的周长 m的取值范围;
(4)得出结论
若能生产出面积为4的矩形模具,则周长m的取值范围为
1-7DDDCDBC
,2 )或(2 , )
10.解:(1)由题意,将点 A(-1,m)代入一次函数 y=x+5,得m=-1+5=4,
∴A(-1,4).将点 A(-1,4)代入 得 =4,解得k=-4.
则反比例函数的解析式为
(2)将一次函数 y=x+5 的图象沿 y轴向下平移b个单位得到的一次函数的解析式为 y=x+5-b.联立 整理得 0.
∵一次函数 y=x+5-b的图象与反比例函数 的图象有且只有一个交点,
∴关于x的一元二次方程 只有一个实数根.
∴此方程的根的判别式 0,
解得 ,则b的值为1或9.
11-12AB
13.6+
14.解:(1)根据题意,点 A(1,a)在正比例函数 y=2x 上,故将点 A(1,a)代入正比例函数 y=2x中,得a=2,故点 A 的坐标为(1,2),点 A又在反比例函数图象上,将A(1,2)代入反比例函数解析式中,得k=2.
(2)A,B为反比例函数与正比例函数的交点,故可得 解得 已知点 A 坐标为(1,2),故点 B 坐标为(﹣1,﹣2),根据两点间距离公式可得 根据已知条件中四边形 ABCD 为菱形,故 AB=AD=2 . AD∥BC∥x轴,则点 D 坐标为(1+2 ,2).
15.解:(1)一 [x,y都是边长,因此,都是正数,故点(x,y)在第一象限.]
(2)图象如图所示.
(3)①8 [把点(2,2)代人 得 解得m=8.]
②在直线平移过程中,交点个数有:0个,1个,2个三种情况.0个交点时,m<8;1个交点时,m=8;2个交点时,m>8.
中小学教育资源及组卷应用平台
(4)m≥8[联立 和 整理,得 时,两个函数有交点,解得 m≥8.]
1-7DDDCDBC
,2 )或(2 , )
10.解:(1)由题意,将点 A(-1,m)代入一次函数 y=x+5,得m=-1+5=4,
∴A(-1,4).将点 A(-1,4)代入 得 =4,解得k=-4.
则反比例函数的解析式为
(2)将一次函数 y=x+5 的图象沿 y轴向下平移b个单位得到的一次函数的解析式为 y=x+5-b.联立 整理得 0.
∵一次函数 y=x+5-b的图象与反比例函数 的图象有且只有一个交点,
∴关于x的一元二次方程 只有一个实数根.
∴此方程的根的判别式 0,
解得 ,则b的值为1或9.
11-12AB
13.6+
14.解:(1)根据题意,点 A(1,a)在正比例函数 y=2x 上,故将点 A(1,a)代入正比例函数 y=2x中,得a=2,故点 A 的坐标为(1,2),点 A又在反比例函数图象上,将A(1,2)代入反比例函数解析式中,得k=2.
(2)A,B为反比例函数与正比例函数的交点,故可得 解得 已知点 A 坐标为(1,2),故点 B 坐标为(﹣1,﹣2),根据两点间距离公式可得 根据已知条件中四边形 ABCD 为菱形,故 AB=AD=2 . AD∥BC∥x轴,则点 D 坐标为(1+2 ,2).
15.解:(1)一 [x,y都是边长,因此,都是正数,故点(x,y)在第一象限.]
(2)图象如图所示.
(3)①8 [把点(2,2)代人 得 解得m=8.]
②在直线平移过程中,交点个数有:0个,1个,2个三种情况.0个交点时,m<8;1个交点时,m=8;2个交点时,m>8.
(4)m≥8[联立 和 整理,得 时,两个函数有交点,解得 m≥8.]
同课章节目录
