2024年陕西省西安市高新逸翠园初级中学中考十六模数学试题(含答案)
文档属性
| 名称 | 2024年陕西省西安市高新逸翠园初级中学中考十六模数学试题(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-10 00:00:00 | ||
图片预览


文档简介
2024年陕西省西安市高新逸翠园初级中学中考十六模数学试题
一.选择题(共8小题,满分24分,每小题3分)
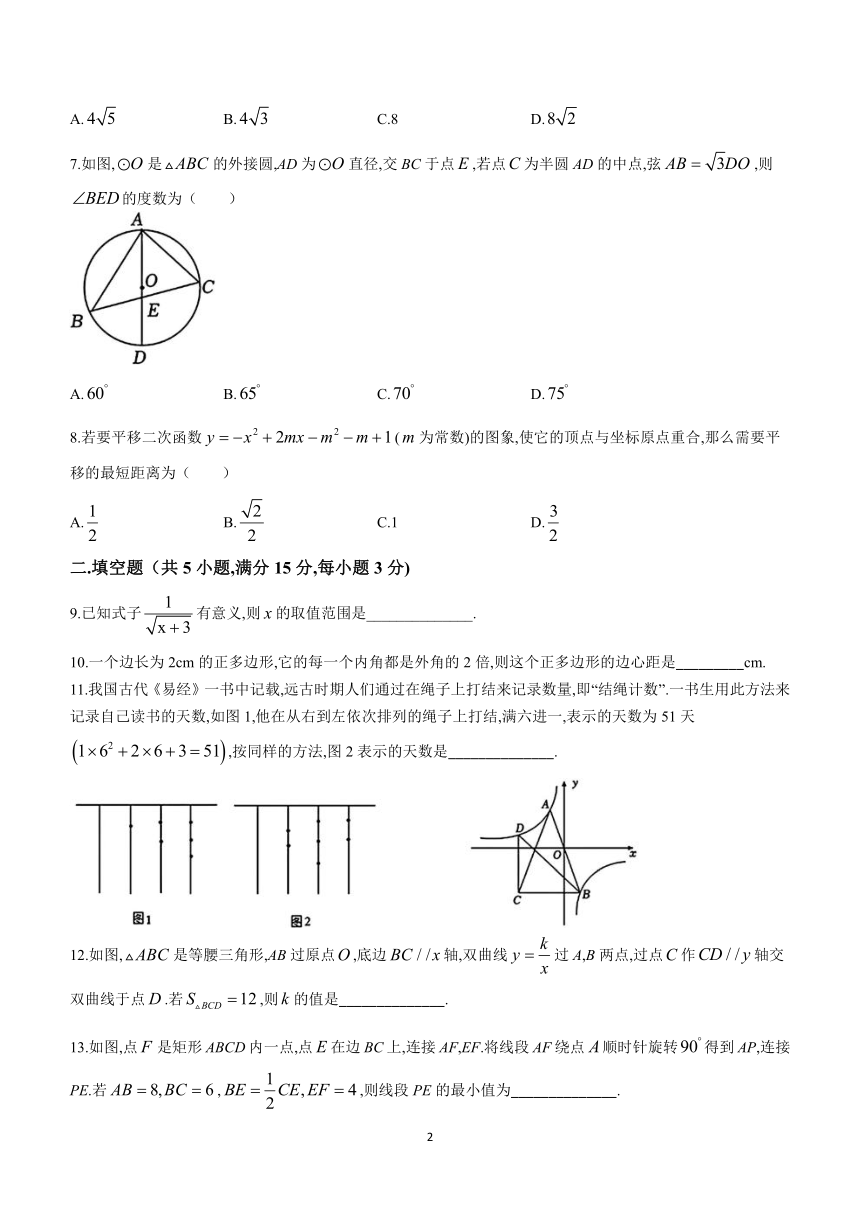
1.下列四个数:,其中最小的一个是( )
A.4 B.-1 C.0 D.
2.如图图形中,是轴对称图形不是中心对称图形的是( )
A. B. C. D.
3.计算( )
A. B. C. D.
4.如图,将一副三角尺按图中所示位置摆放,点在AC上,.则的度数是( )
A. B. C. D.
5.在同一平面直角坐标系中,一次函数与的图象可能是( )
A. B. C. D.
6.如图,已知AE、CD分别是的角平分线和中线,且,垂足为F,G为BE的中点,连接DG,若,则GC的长为( )
A. B. C.8 D.
7.如图,是的外接圆,AD为直径,交BC于点,若点为半圆AD的中点,弦,则的度数为( )
A. B. C. D.
8.若要平移二次函数(为常数)的图象,使它的顶点与坐标原点重合,那么需要平移的最短距离为( )
A. B. C.1 D.
二.填空题(共5小题,满分15分,每小题3分)
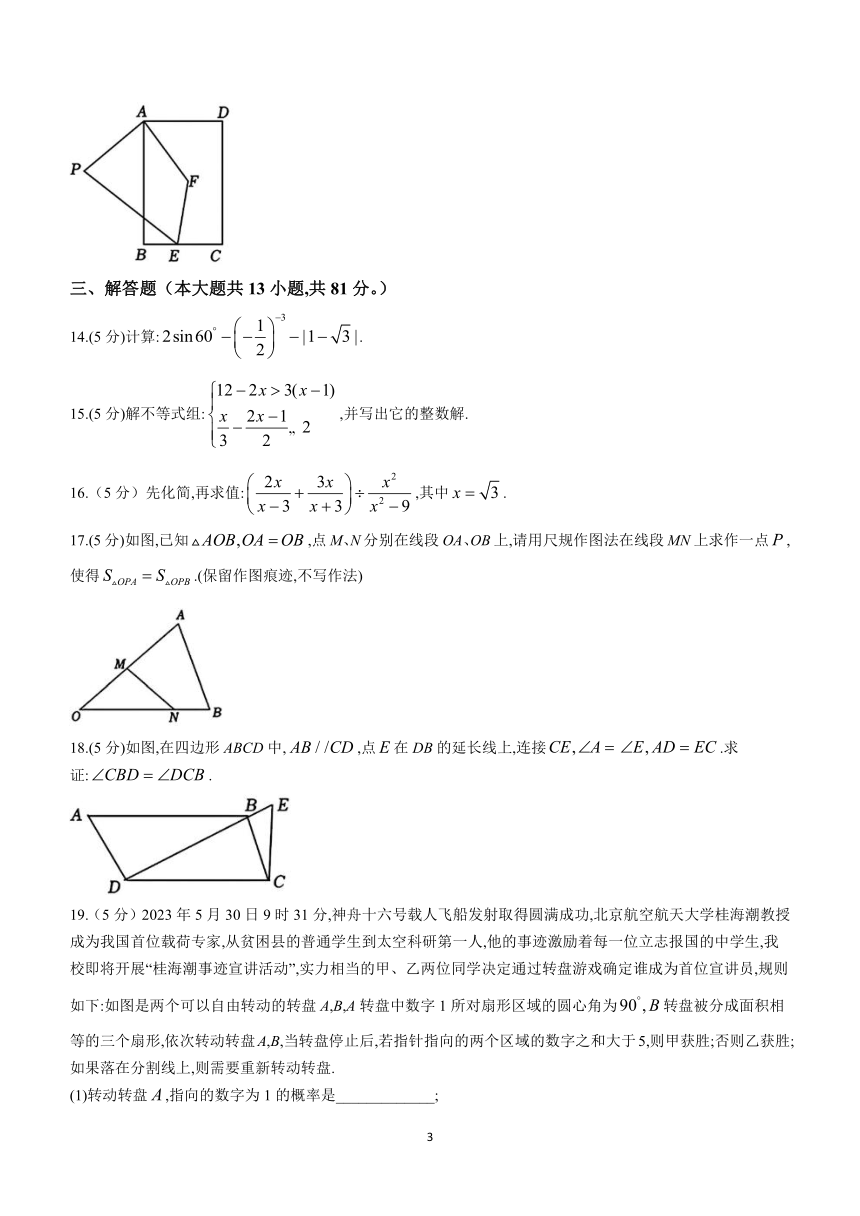
9.已知式子有意义,则的取值范围是______________.
10.一个边长为2cm的正多边形,它的每一个内角都是外角的2倍,则这个正多边形的边心距是_________cm.
11.我国古代《易经》一书中记载,远古时期人们通过在绳子上打结来记录数量,即“结绳计数”.一书生用此方法来记录自己读书的天数,如图1,他在从右到左依次排列的绳子上打结,满六进一,表示的天数为51天,按同样的方法,图2表示的天数是______________.
12.如图,是等腰三角形,AB过原点,底边轴,双曲线过A,B两点,过点作轴交双曲线于点.若,则的值是______________.
13.如图,点是矩形ABCD内一点,点在边BC上,连接AF,EF.将线段AF绕点顺时针旋转得到AP,连接PE.若,,则线段PE的最小值为______________.
三、解答题(本大题共13小题,共81分。)
14.(5分)计算:.
15.(5分)解不等式组:,并写出它的整数解.
16.(5分)先化简,再求值:,其中.
17.(5分)如图,已知,点M、N分别在线段OA、OB上,请用尺规作图法在线段MN上求作一点,使得.(保留作图痕迹,不写作法)
18.(5分)如图,在四边形ABCD中,,点在DB的延长线上,连接.求证:.
19.(5分)2023年5月30日9时31分,神舟十六号载人飞船发射取得圆满成功,北京航空航天大学桂海潮教授成为我国首位载荷专家,从贫困县的普通学生到太空科研第一人,他的事迹激励着每一位立志报国的中学生,我校即将开展“桂海潮事迹宣讲活动”,实力相当的甲、乙两位同学决定通过转盘游戏确定谁成为首位宣讲员,规则如下:如图是两个可以自由转动的转盘A,B,A转盘中数字1所对扇形区域的圆心角为转盘被分成面积相等的三个扇形,依次转动转盘A,B,当转盘停止后,若指针指向的两个区域的数字之和大于5,则甲获胜;否则乙获胜;如果落在分割线上,则需要重新转动转盘.
(1)转动转盘,指向的数字为1的概率是_____________;
(2)试用列表或画树状图的方法说明游戏是否公平.若公平,请说明理由:若不公平,谁获胜的可能性更大
20.(5分)一个两位数,十位数字和个位数字之和是7,如果把十位数字和个位数字对调,那么得到的新两位数比原两位数大45,求原两位数.
21.(6分)春暖花开,正是放风筝的好时节.如图是小明在一次放风筝活动中某时段的示意图,他在A处时的风筝线(整个过程中风筝线近似地看作直线)与水平线构成,线段表示小明身高1.5米.当他从点跑动10米到达点处时,风筝线与水平线构成,此时风筝到达点处,风筝的水平移动距离米,这一过程中风筝线的长度保持不变,求风筝原来的高度(精确到0.1米).(参考数据:)
22.(7分)物理实验技能考核前,小亮对“探究凸透镜成像规律”的实验进行了反复练习,在练习的过程中,他惊喜地发现“蜡烛在燃烧过程中,其剩余高度与燃烧时间之间呈一次函数关系”,已知蜡烛燃烧6分钟后,蜡烛剩余高度;蜡烛燃烧20分钟后,蜡烛剩余高度.
(1)求与的函数表达式:
(2)小亮晚上7时15分点亮一支新蜡烛,但有一段时间风把蜡烛吹灭了,后又点亮蜡烛,至晚上9时15分蜡烛燃烧了一半,问其间蜡烛熄灭了几分钟
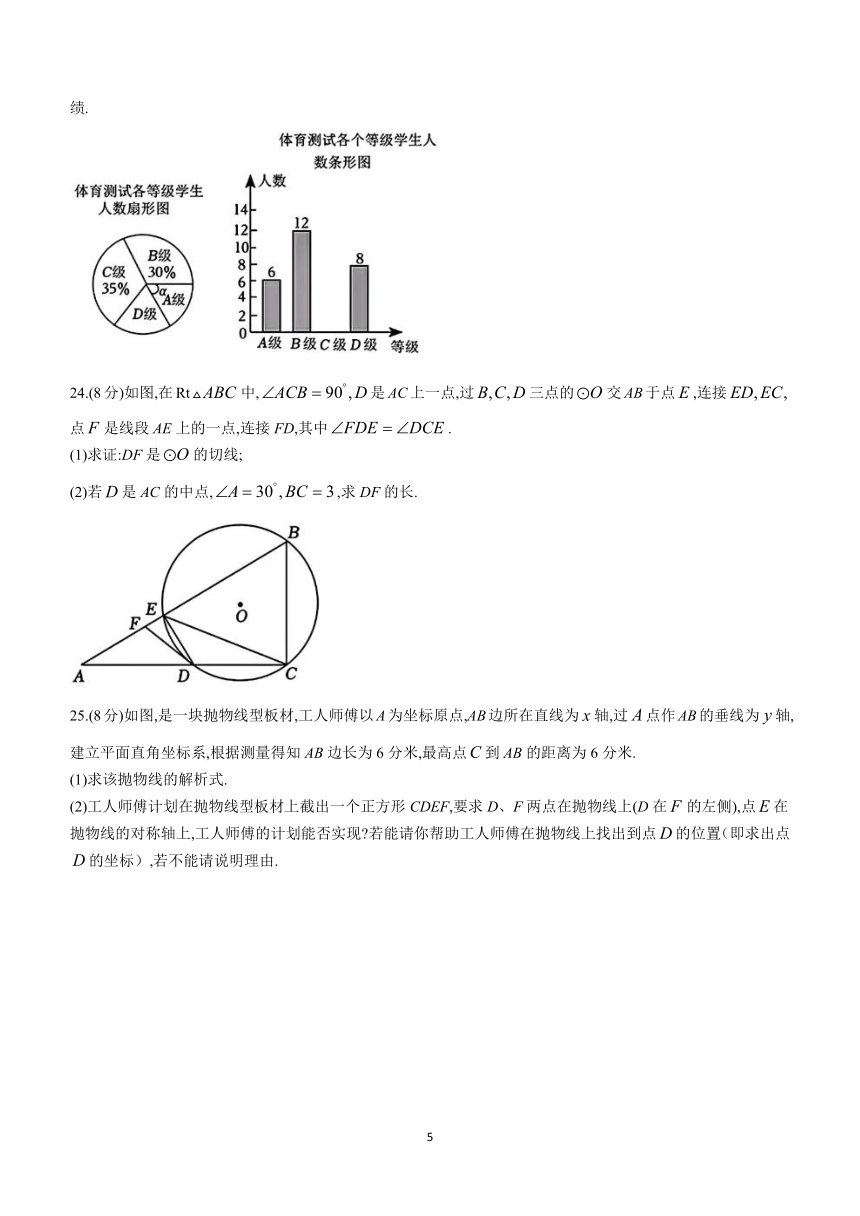
23.(7分)为了解某校八年级体育科目训练情况,从八年级学生中随机抽取了部分学生进行了一次体育科目测试(把测试结果分为四个等级:级:优秀;级:良好;级:及格;级:不及格),并将测试结果绘成了如图两幅不完整的统计图.请根据统计图中的信息解答下列问题:
(1)图1中的度数是___________°,并把图2条形统计图补充完整.
(2)抽取的这部分的学生的体育科目测试结果的中位数是在___________级;
(3)依次将优秀、良好、及格、不及格记为80分、70分、60分、50分,请计算抽取的这部分学生体育的平均成绩.
24.(8分)如图,在Rt中,是AC上一点,过三点的交AB于点,连接点是线段AE上的一点,连接FD,其中.
(1)求证:DF是的切线;
(2)若是AC的中点,,求DF的长.
25.(8分)如图,是一块抛物线型板材,工人师傅以A为坐标原点,AB边所在直线为轴,过点作AB的垂线为轴,建立平面直角坐标系,根据测量得知AB边长为6分米,最高点到AB的距离为6分米.
(1)求该抛物线的解析式.
(2)工人师傅计划在抛物线型板材上截出一个正方形CDEF,要求D、F两点在抛物线上(D在的左侧),点在抛物线的对称轴上,工人师傅的计划能否实现 若能请你帮助工人师傅在抛物线上找出到点的位置(即求出点的坐标),若不能请说明理由.
26.(10分)(1)①如图,已知A、B两点及直线l,P为l上一动点,当的值最小时,请在l上确定P的位置.
②如图,已知及弦AB,C为圆上一动点,当最大时,请在圆上确定C的位置.
(2)如图3,是中心花园的一角,开发商考虑将西侧竖石河景观和南侧街心花园融于日常生活,把沿河风光带包装成社区的公园.在扇形OAB中,米,在围墙OA和OB上分别有两个入口和,且米,是OB的中点,出口在弧AB上.现准备沿CE、DE从入口到出口铺设两条景观小路,在四边形CODE内种花,在剩余区域种草.
①出口E设在距直线OB多远处(即求点E到直线OB的距离)可以使四边形CODE的面积最大 最大面积是多少 (小路宽度不计)
②已知铺设小路CE所用的普通石材每米的造价是200元,铺设小路DE所用的景观石材每米的造价是400元.则在弧AB上是否存在点,使铺设小路CE和DE的总造价最低 若存在,求出最低总造价和出口E距直线OB的距离;若不存在,请说明理由.
高新逸翠园初级中学2023-2024学年度第二学期九年级十六模
数学参考答案
一、选择题
1-4DBBC 5-8DADB
二、填空题
9. 10. 11.92 12.
14.【解答】解:原式
15.【解答】解:,
解不等式①,得:,
解不等式②,得:,
该不等式组的解集为,
该不等式组的整数解是.
16.【解答】
当时,原式.
17.【解答】解:如图,点即为所求.
18.【解答】证明:,
在与中,
19.【解答】解:(1)盘中数字1所对扇形区域的圆心角为,
盘中数字1所对扇形区域占整体的,
转动转盘,指向的数字为1的概率是,
故答案为:;
(2)如图,将盘4等分,这样才是指向每个区域的可能性均等,用列表法表示所有等可能出现的结果如下:
A盘B盘 1 2 2 2
3
4
5
共有12种等可能出现的结果,其中指针指向的两个区域的数字之和大于5,即甲获胜的有7种,所以甲获胜的概率为,乙获胜的概率为,
所以这个游戏不公平,甲获胜的可能性较大.
20.【解答】解:设原两位数的十位数字为,个位数字为,
依题意得:,
解得:,
答:原两位数为16.
21.【解答】解:由题意得:米,米,
设米,
米,
米,
米,
在Rt中,,
米,
在Rt中,,
米
解得:,
(米),
在Rt中,(米),
(米),
风筝原来的高度的长约为11.8米.
22.【解答】解:(1)设与的函数表达式为,
蜡烛燃烧6分钟后,蜡烛剩余高度;蜡烛燃烧20分钟后,蜡烛剩余高度,
解得,
即与的函数表达式为;
(2)将代入,得,
这根蜡烛的长度为,
将代入,得,
到9:15有120分钟,(分钟),
其间蜡烛熄灭了15分钟.
23.【解答】解:(1)被调查的总人数为(人),
则级人数为(人),
补全的条形统计图如图所示,
故答案为:;
(2)这组数据的中位数是第20、21个数据的平均数,而这2个数据均落在级,
抽取的这部分的学生的体育科目测试结果的中位数是在级,
故答案为:;
(3)(分),
答:抽取的这部分学生体育的平均成绩为64分.
24.【解答】(1)证明:,点B,D在上,
是的直径,,
即,
是的切线;
(2)解:如图,,
是AC的中点,
是的直径,
在Rt中,,
在Rt中,,
即
25.【解答】解:(1)∵AB边长为6分米,最高点到AB的距离为6分米.
点的坐标为,
根据抛物线的对称性可知:顶点的坐标为,
设这个抛物线的解析式为:,
将点代入,得:,解得:,
抛物线的解析式为:,
(2)能够实现,点的坐标为:.
点在抛物线上,
可设点的坐标为,
连接DF交CE于点,如图:
四边形CDEF为正方形,
为抛物线的对称轴,点的坐标为,
点的坐标为,
整理得:,
解得:或(不合题意,舍去),
当时,,
点的坐标为.
26.【解答】(1)
(2)解:①如图,作,垂足为,延长OG交弧AB于点,则此时的面积最大.
,点为OB的中点,
在Rt中,,
四边形CODE面积的最大值为;
作,垂足为,
又
出口设在距直线OB的7.2米处可以使四边形CODE的面积最大为60平方米;
②铺设小路CE和DE的总造价为,
如图,连接OE,延长OB到点,使,连接EQ,
在与中,,
,故,
,问题转化为求的最小值,
连接CQ,交弧AB于点,此时取得最小值为CQ,
在Rt中,,
,故总造价的最小值为,
作,垂足为,连接,
设,则,
在Rt中,,
,
解得,(舍去),
∴总造价的最小值为元,出口E距直线OB的距离为米.
一.选择题(共8小题,满分24分,每小题3分)
1.下列四个数:,其中最小的一个是( )
A.4 B.-1 C.0 D.
2.如图图形中,是轴对称图形不是中心对称图形的是( )
A. B. C. D.
3.计算( )
A. B. C. D.
4.如图,将一副三角尺按图中所示位置摆放,点在AC上,.则的度数是( )
A. B. C. D.
5.在同一平面直角坐标系中,一次函数与的图象可能是( )
A. B. C. D.
6.如图,已知AE、CD分别是的角平分线和中线,且,垂足为F,G为BE的中点,连接DG,若,则GC的长为( )
A. B. C.8 D.
7.如图,是的外接圆,AD为直径,交BC于点,若点为半圆AD的中点,弦,则的度数为( )
A. B. C. D.
8.若要平移二次函数(为常数)的图象,使它的顶点与坐标原点重合,那么需要平移的最短距离为( )
A. B. C.1 D.
二.填空题(共5小题,满分15分,每小题3分)
9.已知式子有意义,则的取值范围是______________.
10.一个边长为2cm的正多边形,它的每一个内角都是外角的2倍,则这个正多边形的边心距是_________cm.
11.我国古代《易经》一书中记载,远古时期人们通过在绳子上打结来记录数量,即“结绳计数”.一书生用此方法来记录自己读书的天数,如图1,他在从右到左依次排列的绳子上打结,满六进一,表示的天数为51天,按同样的方法,图2表示的天数是______________.
12.如图,是等腰三角形,AB过原点,底边轴,双曲线过A,B两点,过点作轴交双曲线于点.若,则的值是______________.
13.如图,点是矩形ABCD内一点,点在边BC上,连接AF,EF.将线段AF绕点顺时针旋转得到AP,连接PE.若,,则线段PE的最小值为______________.
三、解答题(本大题共13小题,共81分。)
14.(5分)计算:.
15.(5分)解不等式组:,并写出它的整数解.
16.(5分)先化简,再求值:,其中.
17.(5分)如图,已知,点M、N分别在线段OA、OB上,请用尺规作图法在线段MN上求作一点,使得.(保留作图痕迹,不写作法)
18.(5分)如图,在四边形ABCD中,,点在DB的延长线上,连接.求证:.
19.(5分)2023年5月30日9时31分,神舟十六号载人飞船发射取得圆满成功,北京航空航天大学桂海潮教授成为我国首位载荷专家,从贫困县的普通学生到太空科研第一人,他的事迹激励着每一位立志报国的中学生,我校即将开展“桂海潮事迹宣讲活动”,实力相当的甲、乙两位同学决定通过转盘游戏确定谁成为首位宣讲员,规则如下:如图是两个可以自由转动的转盘A,B,A转盘中数字1所对扇形区域的圆心角为转盘被分成面积相等的三个扇形,依次转动转盘A,B,当转盘停止后,若指针指向的两个区域的数字之和大于5,则甲获胜;否则乙获胜;如果落在分割线上,则需要重新转动转盘.
(1)转动转盘,指向的数字为1的概率是_____________;
(2)试用列表或画树状图的方法说明游戏是否公平.若公平,请说明理由:若不公平,谁获胜的可能性更大
20.(5分)一个两位数,十位数字和个位数字之和是7,如果把十位数字和个位数字对调,那么得到的新两位数比原两位数大45,求原两位数.
21.(6分)春暖花开,正是放风筝的好时节.如图是小明在一次放风筝活动中某时段的示意图,他在A处时的风筝线(整个过程中风筝线近似地看作直线)与水平线构成,线段表示小明身高1.5米.当他从点跑动10米到达点处时,风筝线与水平线构成,此时风筝到达点处,风筝的水平移动距离米,这一过程中风筝线的长度保持不变,求风筝原来的高度(精确到0.1米).(参考数据:)
22.(7分)物理实验技能考核前,小亮对“探究凸透镜成像规律”的实验进行了反复练习,在练习的过程中,他惊喜地发现“蜡烛在燃烧过程中,其剩余高度与燃烧时间之间呈一次函数关系”,已知蜡烛燃烧6分钟后,蜡烛剩余高度;蜡烛燃烧20分钟后,蜡烛剩余高度.
(1)求与的函数表达式:
(2)小亮晚上7时15分点亮一支新蜡烛,但有一段时间风把蜡烛吹灭了,后又点亮蜡烛,至晚上9时15分蜡烛燃烧了一半,问其间蜡烛熄灭了几分钟
23.(7分)为了解某校八年级体育科目训练情况,从八年级学生中随机抽取了部分学生进行了一次体育科目测试(把测试结果分为四个等级:级:优秀;级:良好;级:及格;级:不及格),并将测试结果绘成了如图两幅不完整的统计图.请根据统计图中的信息解答下列问题:
(1)图1中的度数是___________°,并把图2条形统计图补充完整.
(2)抽取的这部分的学生的体育科目测试结果的中位数是在___________级;
(3)依次将优秀、良好、及格、不及格记为80分、70分、60分、50分,请计算抽取的这部分学生体育的平均成绩.
24.(8分)如图,在Rt中,是AC上一点,过三点的交AB于点,连接点是线段AE上的一点,连接FD,其中.
(1)求证:DF是的切线;
(2)若是AC的中点,,求DF的长.
25.(8分)如图,是一块抛物线型板材,工人师傅以A为坐标原点,AB边所在直线为轴,过点作AB的垂线为轴,建立平面直角坐标系,根据测量得知AB边长为6分米,最高点到AB的距离为6分米.
(1)求该抛物线的解析式.
(2)工人师傅计划在抛物线型板材上截出一个正方形CDEF,要求D、F两点在抛物线上(D在的左侧),点在抛物线的对称轴上,工人师傅的计划能否实现 若能请你帮助工人师傅在抛物线上找出到点的位置(即求出点的坐标),若不能请说明理由.
26.(10分)(1)①如图,已知A、B两点及直线l,P为l上一动点,当的值最小时,请在l上确定P的位置.
②如图,已知及弦AB,C为圆上一动点,当最大时,请在圆上确定C的位置.
(2)如图3,是中心花园的一角,开发商考虑将西侧竖石河景观和南侧街心花园融于日常生活,把沿河风光带包装成社区的公园.在扇形OAB中,米,在围墙OA和OB上分别有两个入口和,且米,是OB的中点,出口在弧AB上.现准备沿CE、DE从入口到出口铺设两条景观小路,在四边形CODE内种花,在剩余区域种草.
①出口E设在距直线OB多远处(即求点E到直线OB的距离)可以使四边形CODE的面积最大 最大面积是多少 (小路宽度不计)
②已知铺设小路CE所用的普通石材每米的造价是200元,铺设小路DE所用的景观石材每米的造价是400元.则在弧AB上是否存在点,使铺设小路CE和DE的总造价最低 若存在,求出最低总造价和出口E距直线OB的距离;若不存在,请说明理由.
高新逸翠园初级中学2023-2024学年度第二学期九年级十六模
数学参考答案
一、选择题
1-4DBBC 5-8DADB
二、填空题
9. 10. 11.92 12.
14.【解答】解:原式
15.【解答】解:,
解不等式①,得:,
解不等式②,得:,
该不等式组的解集为,
该不等式组的整数解是.
16.【解答】
当时,原式.
17.【解答】解:如图,点即为所求.
18.【解答】证明:,
在与中,
19.【解答】解:(1)盘中数字1所对扇形区域的圆心角为,
盘中数字1所对扇形区域占整体的,
转动转盘,指向的数字为1的概率是,
故答案为:;
(2)如图,将盘4等分,这样才是指向每个区域的可能性均等,用列表法表示所有等可能出现的结果如下:
A盘B盘 1 2 2 2
3
4
5
共有12种等可能出现的结果,其中指针指向的两个区域的数字之和大于5,即甲获胜的有7种,所以甲获胜的概率为,乙获胜的概率为,
所以这个游戏不公平,甲获胜的可能性较大.
20.【解答】解:设原两位数的十位数字为,个位数字为,
依题意得:,
解得:,
答:原两位数为16.
21.【解答】解:由题意得:米,米,
设米,
米,
米,
米,
在Rt中,,
米,
在Rt中,,
米
解得:,
(米),
在Rt中,(米),
(米),
风筝原来的高度的长约为11.8米.
22.【解答】解:(1)设与的函数表达式为,
蜡烛燃烧6分钟后,蜡烛剩余高度;蜡烛燃烧20分钟后,蜡烛剩余高度,
解得,
即与的函数表达式为;
(2)将代入,得,
这根蜡烛的长度为,
将代入,得,
到9:15有120分钟,(分钟),
其间蜡烛熄灭了15分钟.
23.【解答】解:(1)被调查的总人数为(人),
则级人数为(人),
补全的条形统计图如图所示,
故答案为:;
(2)这组数据的中位数是第20、21个数据的平均数,而这2个数据均落在级,
抽取的这部分的学生的体育科目测试结果的中位数是在级,
故答案为:;
(3)(分),
答:抽取的这部分学生体育的平均成绩为64分.
24.【解答】(1)证明:,点B,D在上,
是的直径,,
即,
是的切线;
(2)解:如图,,
是AC的中点,
是的直径,
在Rt中,,
在Rt中,,
即
25.【解答】解:(1)∵AB边长为6分米,最高点到AB的距离为6分米.
点的坐标为,
根据抛物线的对称性可知:顶点的坐标为,
设这个抛物线的解析式为:,
将点代入,得:,解得:,
抛物线的解析式为:,
(2)能够实现,点的坐标为:.
点在抛物线上,
可设点的坐标为,
连接DF交CE于点,如图:
四边形CDEF为正方形,
为抛物线的对称轴,点的坐标为,
点的坐标为,
整理得:,
解得:或(不合题意,舍去),
当时,,
点的坐标为.
26.【解答】(1)
(2)解:①如图,作,垂足为,延长OG交弧AB于点,则此时的面积最大.
,点为OB的中点,
在Rt中,,
四边形CODE面积的最大值为;
作,垂足为,
又
出口设在距直线OB的7.2米处可以使四边形CODE的面积最大为60平方米;
②铺设小路CE和DE的总造价为,
如图,连接OE,延长OB到点,使,连接EQ,
在与中,,
,故,
,问题转化为求的最小值,
连接CQ,交弧AB于点,此时取得最小值为CQ,
在Rt中,,
,故总造价的最小值为,
作,垂足为,连接,
设,则,
在Rt中,,
,
解得,(舍去),
∴总造价的最小值为元,出口E距直线OB的距离为米.
同课章节目录
