沪教版六年级数学下册试题 第八章《长方体的再认识》单元复习题(含答案)
文档属性
| 名称 | 沪教版六年级数学下册试题 第八章《长方体的再认识》单元复习题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 106.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-10 00:00:00 | ||
图片预览




文档简介
第八章《长方体的再认识》单元复习题
一、单选题
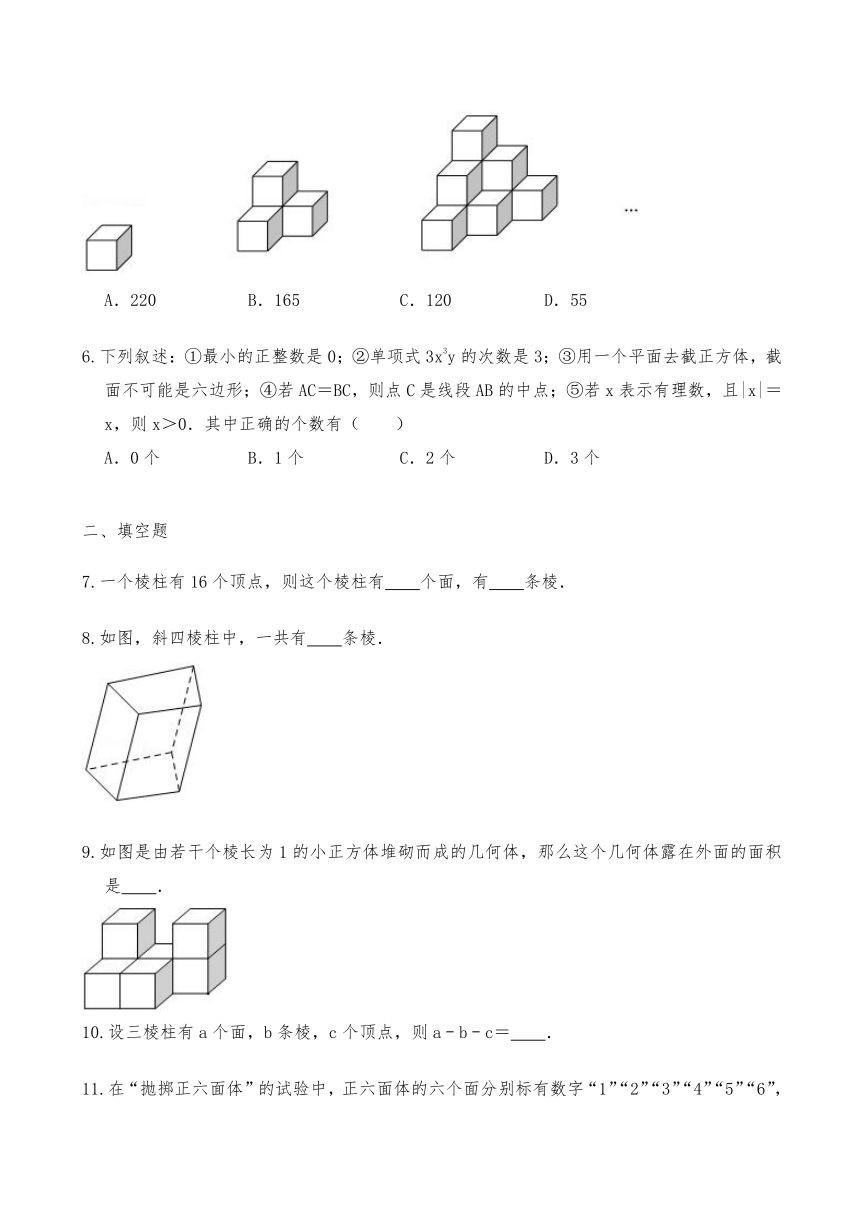
1.下列几何体中,是圆锥的为( )
A. B.
C. D.
2.在一个棱柱中,一共有八个面,则这个棱柱棱的条数有( )
A.18条 B.15条 C.12条 D.21条
3.我们知道,面动成体!如图,正方形ABCD边长为3cm,以直线AB为轴将正方形旋转一周所得几何体,从正面看到的形状图的面积是( )
A.9cm2 B.18cm2 C.9πcm2 D.27πcm2
4.下列说法错误的是( )
A.一枚硬币在光滑的桌面上快速旋转,像形成一个球,用“面动成体”来解释
B.流星划过天空时留下一道明亮的光线,用“线动成面”来解释
C.把弯曲的公路改直,就能缩短路程,用“两点之间线段最短”来解释
D.将一根细木条固定在墙上,至少需要两个钉子,用“两点确定一条直线”来解释
5.如图,都是由棱长为1的正方体叠成的图形.例如:第1个图形由1个正方体叠成,第2个图形由4个正方体叠成,第3个图形由10个正方体叠成,…,依次规律,第10个图形由n个正方体叠成,则n的值为( )
A.220 B.165 C.120 D.55
6.下列叙述:①最小的正整数是0;②单项式3x3y的次数是3;③用一个平面去截正方体,截面不可能是六边形;④若AC=BC,则点C是线段AB的中点;⑤若x表示有理数,且|x|=x,则x>0.其中正确的个数有( )
A.0个 B.1个 C.2个 D.3个
二、填空题
7.一个棱柱有16个顶点,则这个棱柱有 个面,有 条棱.
8.如图,斜四棱柱中,一共有 条棱.
9.如图是由若干个棱长为1的小正方体堆砌而成的几何体,那么这个几何体露在外面的面积是 .
10.设三棱柱有a个面,b条棱,c个顶点,则a﹣b﹣c= .
11.在“抛掷正六面体”的试验中,正六面体的六个面分别标有数字“1”“2”“3”“4”“5”“6”,在试验次数很大时,数字“6”朝上的频率稳定在 .
12.将一个高为8.底面半径为3的实心圆柱体铸铁零件改造成一个实心正方体零件(改造过程中损耗忽略不计),则改造后的正方体的棱长为 (π取3)
13.如图,长方形的长为3cm,宽为2cm,分别以该长方形的一边所在直线为轴,将其旋转一周,形成圆柱,其体积为 cm3.(结果保留π)
14.观察如图所示的长方体,用符号(“∥”或“⊥”)表示下列两棱的位置关系:AD BC,AB AA1,AB C1D1.
15.如图,一个长方体长9cm,宽5cm,高4cm.从这个长方体的一个角上挖掉一个棱长3cm的正方体,剩下部分的体积是 cm3,剩下部分的表面积是 cm2.
16.已知长方形的长为5,宽为2,将其绕它的一条边所在的直线旋转一周,得到一个几何体,该几何体的体积为 (结果保留π).
17.如图,正方体的每条棱上放置相同数目的小球,设每条棱上的小球数为a,则正方体上小球总数为 (用含a的代数式表示).
18.如图,在一次数学活动课上,张明用10个边长为1的小正方形搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 个小立方体,王亮所搭几何体的表面积为 .
三、解答题
19.我们知道,对于一些立体图形问题,常把它转化为平面图形来研究和处理,棱长为a的正方体摆成如图所示的形状,问:
(1)这个几何体共有几个正方体?
(2)这个几何体的表面积是多少?
20.在一个底面直径为5cm,高为16cm圆柱形瓶内装满水,再将瓶内的水倒入一个底面直径为6cm,高为10cm的圆柱形玻璃杯中,能否完全装下?若装不下,求瓶内水面还有多高?若未能装满,求玻璃杯内水面离杯口的距离?
21.按要求完成下题
(1)求圆柱的表面积和体积.(结果保留π)
(2)在边长是4厘米的正方形内画一个最大的圆,求图中阴影部分的面积.(π取3.14)
22.假设圆柱的高是5cm,圆柱的底面半径由小到大变化时,
(1)圆柱的体积如何变化?在这个变化的过程中,自变量、因变量各是什么?
(2)如果圆柱底面半径为r(cm),那么圆柱的体积V(cm3)可以表示为
(3)当r由1cm变化到10cm时,V由 cm3变化到 cm3.
23.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.
(1)以直线BC为轴,把△ABC旋转一周,求所得圆锥的底面圆周长.
(2)以直线AC为轴,把△ABC旋转一周,求所得圆锥的侧面积;
24.做大小两个长方体纸盒,尺寸如下(单位:cm)
长 宽 高
小纸盒 a b c
大纸盒 4a 2.5b 2c
(1)做这两个纸盒共用料多少平方厘来?
(2)做大纸盒比做小纸盒多用料多少平方厘米?
(3)若a=6,b=5,c=3,则大纸盒的体积是多少cm3?
25.【知识生成】我们知道,用两种不同的方法计算同一个几何图形的面积,可以得到一些代数恒等式.
例如:图1可以得到(a+b)2=a2+2ab+b2基于此,请解答下列问题:
(1)根据图2,写出一个代数恒等式:(a+b+c)2 ;
(2)利用(1)中得到的结论,解决下面的问题:若a+b+c=12,ab+bc+ac=27,则a2+b2+c2= ;
(3)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a、b的长方形纸片拼出一个面积为(2a+b)(a+3b)的长方形,则x+y+z= ;
【知识迁移】(4)类似地,用两种不同的方法计算几何体的体积同样可以得到一些代数恒等式.图4表示的是一个边长为x的正方体挖去一个边长为2的小长方体后重新拼成一个新长方体.请你根据图4中两个图形的变化关系,写出一个代数恒等式: .
答案
一、单选题
1.B 2.A 3.B 4.B 5.A 6.A
二、填空题
7.10 24
【分析】根据棱柱的顶点数、面数、棱数之间的关系得出答案.
【解答】解:∵棱柱有16个顶点,
∴这个棱柱是八棱柱,
∴八棱柱有8+2=10个面,有8×3=24条棱,
故答案为:10,24.
8.12
【分析】根据斜四棱柱的特点可得答案.
【解答】解:斜四棱柱中,一共有3×4=12条棱.
故答案为:12.
9.23
【分析】根据简单组合体的三视图的面积,得出该几何体的露在外面的面积.
【解答】解:(5+3)×2+5+2=23,
故答案为:23.
10.-10
【分析】根据三棱柱的特征得出a、b、c的值,代入计算即可.
【解答】解:三棱柱有5个面,9条棱,6个顶点,
因此a=5,b=9,c=6,
所以a﹣b﹣c=5﹣9﹣6=﹣10,
故答案为:﹣10.
11.随着试验次数的增多,变化趋势接近于理论上的概率.
【解答】解:在试验次数很大时,数字“6”朝上的频率的变化趋势接近的值是.
故答案为:.
12.6
【分析】设改造后的正方体的棱长为x,根据题意可得正方体的体积=实心圆柱体体积,然后列出方程,再解即可.
【解答】解:设改造后的正方体的棱长为x,
由题意得:π×32×8=x3,
x3=π×9×8,
x3=3×9×8,
x=6,
故答案为:6.
13.12π或18π
【分析】根据圆柱体的体积=底面积×高求解,再利用圆柱体侧面积求法得出答案.
【解答】解:由题可得,
当以该长方形的长所在直线为轴时V=π 22×3=12π,
当以该长方形的宽所在直线为轴,V=π 32×2=18π,
故答案为:12π或18π.
14.∥ ⊥ ∥
【分析】根据垂直、平行的定义进行判断即可.
【解答】解:在平面A﹣B﹣C﹣D中,直线AD、BC无公共点,因此AD∥BC,
在平面A﹣B﹣A1﹣B1中,直线AB、AA⊥相交成直角,因此AB⊥AA1,
AB和C1D1是异面直线,根据异面直线的位置关系可得AB∥C1D1,
故答案为:∥,⊥,∥.
15.153 202
【分析】根据长方体的体积减去正方体的体积即可求出剩下部分的体积;进而可以求出剩下部分的表面积.
【解答】解:∵长方体长9cm,宽5cm,高4cm体积为:
9×5×4=180cm3.
棱长3cm的正方体体积为27cm3,
∴剩下部分的体积为:
180﹣27=153cm3;
剩下部分的表面积为:
2(9×5+9×4+5×4)
=202(cm2).
故答案为153,202.
16.50π或20π
【分析】旋转后的几何体是圆柱体,先确定出圆柱的底面半径和高,再根据圆柱的体积公式计算即可求解.
【解答】解:长方形绕一边旋转一周,得圆柱.
情况①:π×52×2=50π(cm3);
情况②:π×22×5=20π(cm3);
故答案为:50π或20π.
17.12a-16
【分析】每条棱上有a个小球,12条棱就有12a个小球,这时,每个顶点处的小球被多计算了2次,于是可得答案.
【解答】解:因为正方体有12条棱,
所以12条棱上有12a个小球,
但每个顶点处的小球被多计算2次,8个顶点就被多计算2×8=16次,
所以正方体上小球总数为12a﹣16,
故答案为:12a﹣16.
18.17 48
【分析】最小的大正方体是由小方块组成的3×3×3的大正方体,据此可得王亮至少需要27﹣10=17个小立方体.根据题意得到题中堆积体的俯视图,并进行标数(地图标数法),即可得出王亮所搭几何体的表面积为(8+8+8)×2=48.
【解答】解:由题可知,最小的大正方体是由小方块组成的3×3×3的大正方体,
所以按照张明的要求搭几何体,王亮至少需要27﹣10=17个小立方体.
根据题意得到题中堆积体的俯视图,并进行标数(地图标数法):
由上图的俯视图可知,能将其补充为完整的3×3×3的大正方体的剩余部分的俯视图为:
由此可得,王亮所做堆积体的三视图,主、左、俯三视图面积皆为8,
所以王亮所搭几何体的表面积为(8+8+8)×2=48,
故答案为:17,48.
三、解答题
19.解:(1)上面一层有1个正方体,中间层有3个正方体,底层有6个正方体,共10个正方体;
(2)根据以上分析该物体的表面积为6×6×a2=36a2.
20.解:设将瓶内的水倒入一个底面直径是6cm,高是10cm的圆柱形玻璃杯中时,水面高为xcm,
根据题意得π ()2 x=π ()2×16,
解得x=,
∵>10,
∴不能完全装下.
﹣10=(cm),
16×=1.6(cm),
答:装不下,那么瓶内水面还有1.6cm.
21.解:(1)圆柱的表面积=8π×8+2 π 42=96π平方分米,圆柱的体积=π×42×8=108π立方分米;
(2)图中阴影部分的面积=4×4﹣π×22=16﹣4π≈3.44平方厘米.
22.解:(1)圆柱的体积随着圆柱的底面半径的增大而增大.
自变量:圆柱的底面半径 因变量:圆柱的体积
(2)圆柱的体积等于底面积乘以高,
∴V=5πr2,
故答案为:5πr2;
(3)当r=1cm时,V=5πr2=5π,
当r=10cm时,V=5πr2=500π,
故答案为:5π,500π.
23.解:(1)2π×6=12π.
(2)∵∠C=90°,AC=6,BC=8,
∴AB==10,
所以以直线AC为轴,把△ABC旋转一周,得到的圆锥的侧面积=×10×2π×8=80π;
24.解:(1)做这两个纸盒共用料(单位:cm2)(2ab+2bc+2ac)+(20ab+16ac+10bc),
=2ab+2bc+2ac+20ab+16ac+10bc,
=22ab+12bc+18ac;
(2)做大纸盒比做小纸盒多用料(单位:cm2),
(20ab+16ac+10bc)﹣(2ab+2bc+2ac)
=20ab+10bc+16ac﹣2ab﹣2bc﹣2ac
=18ab+8bc+14ac;
(3)大纸盒的体积V=4a×2.5b×2c=20abc,
当a=6,b=5,c=3时V=20×6×5×3=1800cm3.
25.解:(1)由图2得:正方形的面积=(a+b+c)2;正方形的面积=a2+b2+c2+2ab+2ac+2bc,
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,
故答案为:=a2+b2+c2+2ab+2ac+2bc;
(2)∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,
∵a+b+c=12,ab+ac+bc=27,
∴122=a2+b2+c2+2×27,
∴a2+b2+c2=144﹣54=90,
故答案为:90;
(3)由题意得:(2a+b)(a+3b)=xa2+yb2+zab,
∴2a2+7ab+3b2=xa2+yb2+zab,
∴,
∴x+y+z=12,
故答案为:12;
(4)∵原几何体的体积=x3﹣2×2 x=x3﹣4x,新几何体的体积=x(x+2)(x﹣2),
∴x3﹣4x=x(x+2)(x﹣2).
故答案为:x3﹣4x=x(x+2)(x﹣2).
一、单选题
1.下列几何体中,是圆锥的为( )
A. B.
C. D.
2.在一个棱柱中,一共有八个面,则这个棱柱棱的条数有( )
A.18条 B.15条 C.12条 D.21条
3.我们知道,面动成体!如图,正方形ABCD边长为3cm,以直线AB为轴将正方形旋转一周所得几何体,从正面看到的形状图的面积是( )
A.9cm2 B.18cm2 C.9πcm2 D.27πcm2
4.下列说法错误的是( )
A.一枚硬币在光滑的桌面上快速旋转,像形成一个球,用“面动成体”来解释
B.流星划过天空时留下一道明亮的光线,用“线动成面”来解释
C.把弯曲的公路改直,就能缩短路程,用“两点之间线段最短”来解释
D.将一根细木条固定在墙上,至少需要两个钉子,用“两点确定一条直线”来解释
5.如图,都是由棱长为1的正方体叠成的图形.例如:第1个图形由1个正方体叠成,第2个图形由4个正方体叠成,第3个图形由10个正方体叠成,…,依次规律,第10个图形由n个正方体叠成,则n的值为( )
A.220 B.165 C.120 D.55
6.下列叙述:①最小的正整数是0;②单项式3x3y的次数是3;③用一个平面去截正方体,截面不可能是六边形;④若AC=BC,则点C是线段AB的中点;⑤若x表示有理数,且|x|=x,则x>0.其中正确的个数有( )
A.0个 B.1个 C.2个 D.3个
二、填空题
7.一个棱柱有16个顶点,则这个棱柱有 个面,有 条棱.
8.如图,斜四棱柱中,一共有 条棱.
9.如图是由若干个棱长为1的小正方体堆砌而成的几何体,那么这个几何体露在外面的面积是 .
10.设三棱柱有a个面,b条棱,c个顶点,则a﹣b﹣c= .
11.在“抛掷正六面体”的试验中,正六面体的六个面分别标有数字“1”“2”“3”“4”“5”“6”,在试验次数很大时,数字“6”朝上的频率稳定在 .
12.将一个高为8.底面半径为3的实心圆柱体铸铁零件改造成一个实心正方体零件(改造过程中损耗忽略不计),则改造后的正方体的棱长为 (π取3)
13.如图,长方形的长为3cm,宽为2cm,分别以该长方形的一边所在直线为轴,将其旋转一周,形成圆柱,其体积为 cm3.(结果保留π)
14.观察如图所示的长方体,用符号(“∥”或“⊥”)表示下列两棱的位置关系:AD BC,AB AA1,AB C1D1.
15.如图,一个长方体长9cm,宽5cm,高4cm.从这个长方体的一个角上挖掉一个棱长3cm的正方体,剩下部分的体积是 cm3,剩下部分的表面积是 cm2.
16.已知长方形的长为5,宽为2,将其绕它的一条边所在的直线旋转一周,得到一个几何体,该几何体的体积为 (结果保留π).
17.如图,正方体的每条棱上放置相同数目的小球,设每条棱上的小球数为a,则正方体上小球总数为 (用含a的代数式表示).
18.如图,在一次数学活动课上,张明用10个边长为1的小正方形搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 个小立方体,王亮所搭几何体的表面积为 .
三、解答题
19.我们知道,对于一些立体图形问题,常把它转化为平面图形来研究和处理,棱长为a的正方体摆成如图所示的形状,问:
(1)这个几何体共有几个正方体?
(2)这个几何体的表面积是多少?
20.在一个底面直径为5cm,高为16cm圆柱形瓶内装满水,再将瓶内的水倒入一个底面直径为6cm,高为10cm的圆柱形玻璃杯中,能否完全装下?若装不下,求瓶内水面还有多高?若未能装满,求玻璃杯内水面离杯口的距离?
21.按要求完成下题
(1)求圆柱的表面积和体积.(结果保留π)
(2)在边长是4厘米的正方形内画一个最大的圆,求图中阴影部分的面积.(π取3.14)
22.假设圆柱的高是5cm,圆柱的底面半径由小到大变化时,
(1)圆柱的体积如何变化?在这个变化的过程中,自变量、因变量各是什么?
(2)如果圆柱底面半径为r(cm),那么圆柱的体积V(cm3)可以表示为
(3)当r由1cm变化到10cm时,V由 cm3变化到 cm3.
23.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.
(1)以直线BC为轴,把△ABC旋转一周,求所得圆锥的底面圆周长.
(2)以直线AC为轴,把△ABC旋转一周,求所得圆锥的侧面积;
24.做大小两个长方体纸盒,尺寸如下(单位:cm)
长 宽 高
小纸盒 a b c
大纸盒 4a 2.5b 2c
(1)做这两个纸盒共用料多少平方厘来?
(2)做大纸盒比做小纸盒多用料多少平方厘米?
(3)若a=6,b=5,c=3,则大纸盒的体积是多少cm3?
25.【知识生成】我们知道,用两种不同的方法计算同一个几何图形的面积,可以得到一些代数恒等式.
例如:图1可以得到(a+b)2=a2+2ab+b2基于此,请解答下列问题:
(1)根据图2,写出一个代数恒等式:(a+b+c)2 ;
(2)利用(1)中得到的结论,解决下面的问题:若a+b+c=12,ab+bc+ac=27,则a2+b2+c2= ;
(3)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a、b的长方形纸片拼出一个面积为(2a+b)(a+3b)的长方形,则x+y+z= ;
【知识迁移】(4)类似地,用两种不同的方法计算几何体的体积同样可以得到一些代数恒等式.图4表示的是一个边长为x的正方体挖去一个边长为2的小长方体后重新拼成一个新长方体.请你根据图4中两个图形的变化关系,写出一个代数恒等式: .
答案
一、单选题
1.B 2.A 3.B 4.B 5.A 6.A
二、填空题
7.10 24
【分析】根据棱柱的顶点数、面数、棱数之间的关系得出答案.
【解答】解:∵棱柱有16个顶点,
∴这个棱柱是八棱柱,
∴八棱柱有8+2=10个面,有8×3=24条棱,
故答案为:10,24.
8.12
【分析】根据斜四棱柱的特点可得答案.
【解答】解:斜四棱柱中,一共有3×4=12条棱.
故答案为:12.
9.23
【分析】根据简单组合体的三视图的面积,得出该几何体的露在外面的面积.
【解答】解:(5+3)×2+5+2=23,
故答案为:23.
10.-10
【分析】根据三棱柱的特征得出a、b、c的值,代入计算即可.
【解答】解:三棱柱有5个面,9条棱,6个顶点,
因此a=5,b=9,c=6,
所以a﹣b﹣c=5﹣9﹣6=﹣10,
故答案为:﹣10.
11.随着试验次数的增多,变化趋势接近于理论上的概率.
【解答】解:在试验次数很大时,数字“6”朝上的频率的变化趋势接近的值是.
故答案为:.
12.6
【分析】设改造后的正方体的棱长为x,根据题意可得正方体的体积=实心圆柱体体积,然后列出方程,再解即可.
【解答】解:设改造后的正方体的棱长为x,
由题意得:π×32×8=x3,
x3=π×9×8,
x3=3×9×8,
x=6,
故答案为:6.
13.12π或18π
【分析】根据圆柱体的体积=底面积×高求解,再利用圆柱体侧面积求法得出答案.
【解答】解:由题可得,
当以该长方形的长所在直线为轴时V=π 22×3=12π,
当以该长方形的宽所在直线为轴,V=π 32×2=18π,
故答案为:12π或18π.
14.∥ ⊥ ∥
【分析】根据垂直、平行的定义进行判断即可.
【解答】解:在平面A﹣B﹣C﹣D中,直线AD、BC无公共点,因此AD∥BC,
在平面A﹣B﹣A1﹣B1中,直线AB、AA⊥相交成直角,因此AB⊥AA1,
AB和C1D1是异面直线,根据异面直线的位置关系可得AB∥C1D1,
故答案为:∥,⊥,∥.
15.153 202
【分析】根据长方体的体积减去正方体的体积即可求出剩下部分的体积;进而可以求出剩下部分的表面积.
【解答】解:∵长方体长9cm,宽5cm,高4cm体积为:
9×5×4=180cm3.
棱长3cm的正方体体积为27cm3,
∴剩下部分的体积为:
180﹣27=153cm3;
剩下部分的表面积为:
2(9×5+9×4+5×4)
=202(cm2).
故答案为153,202.
16.50π或20π
【分析】旋转后的几何体是圆柱体,先确定出圆柱的底面半径和高,再根据圆柱的体积公式计算即可求解.
【解答】解:长方形绕一边旋转一周,得圆柱.
情况①:π×52×2=50π(cm3);
情况②:π×22×5=20π(cm3);
故答案为:50π或20π.
17.12a-16
【分析】每条棱上有a个小球,12条棱就有12a个小球,这时,每个顶点处的小球被多计算了2次,于是可得答案.
【解答】解:因为正方体有12条棱,
所以12条棱上有12a个小球,
但每个顶点处的小球被多计算2次,8个顶点就被多计算2×8=16次,
所以正方体上小球总数为12a﹣16,
故答案为:12a﹣16.
18.17 48
【分析】最小的大正方体是由小方块组成的3×3×3的大正方体,据此可得王亮至少需要27﹣10=17个小立方体.根据题意得到题中堆积体的俯视图,并进行标数(地图标数法),即可得出王亮所搭几何体的表面积为(8+8+8)×2=48.
【解答】解:由题可知,最小的大正方体是由小方块组成的3×3×3的大正方体,
所以按照张明的要求搭几何体,王亮至少需要27﹣10=17个小立方体.
根据题意得到题中堆积体的俯视图,并进行标数(地图标数法):
由上图的俯视图可知,能将其补充为完整的3×3×3的大正方体的剩余部分的俯视图为:
由此可得,王亮所做堆积体的三视图,主、左、俯三视图面积皆为8,
所以王亮所搭几何体的表面积为(8+8+8)×2=48,
故答案为:17,48.
三、解答题
19.解:(1)上面一层有1个正方体,中间层有3个正方体,底层有6个正方体,共10个正方体;
(2)根据以上分析该物体的表面积为6×6×a2=36a2.
20.解:设将瓶内的水倒入一个底面直径是6cm,高是10cm的圆柱形玻璃杯中时,水面高为xcm,
根据题意得π ()2 x=π ()2×16,
解得x=,
∵>10,
∴不能完全装下.
﹣10=(cm),
16×=1.6(cm),
答:装不下,那么瓶内水面还有1.6cm.
21.解:(1)圆柱的表面积=8π×8+2 π 42=96π平方分米,圆柱的体积=π×42×8=108π立方分米;
(2)图中阴影部分的面积=4×4﹣π×22=16﹣4π≈3.44平方厘米.
22.解:(1)圆柱的体积随着圆柱的底面半径的增大而增大.
自变量:圆柱的底面半径 因变量:圆柱的体积
(2)圆柱的体积等于底面积乘以高,
∴V=5πr2,
故答案为:5πr2;
(3)当r=1cm时,V=5πr2=5π,
当r=10cm时,V=5πr2=500π,
故答案为:5π,500π.
23.解:(1)2π×6=12π.
(2)∵∠C=90°,AC=6,BC=8,
∴AB==10,
所以以直线AC为轴,把△ABC旋转一周,得到的圆锥的侧面积=×10×2π×8=80π;
24.解:(1)做这两个纸盒共用料(单位:cm2)(2ab+2bc+2ac)+(20ab+16ac+10bc),
=2ab+2bc+2ac+20ab+16ac+10bc,
=22ab+12bc+18ac;
(2)做大纸盒比做小纸盒多用料(单位:cm2),
(20ab+16ac+10bc)﹣(2ab+2bc+2ac)
=20ab+10bc+16ac﹣2ab﹣2bc﹣2ac
=18ab+8bc+14ac;
(3)大纸盒的体积V=4a×2.5b×2c=20abc,
当a=6,b=5,c=3时V=20×6×5×3=1800cm3.
25.解:(1)由图2得:正方形的面积=(a+b+c)2;正方形的面积=a2+b2+c2+2ab+2ac+2bc,
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,
故答案为:=a2+b2+c2+2ab+2ac+2bc;
(2)∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,
∵a+b+c=12,ab+ac+bc=27,
∴122=a2+b2+c2+2×27,
∴a2+b2+c2=144﹣54=90,
故答案为:90;
(3)由题意得:(2a+b)(a+3b)=xa2+yb2+zab,
∴2a2+7ab+3b2=xa2+yb2+zab,
∴,
∴x+y+z=12,
故答案为:12;
(4)∵原几何体的体积=x3﹣2×2 x=x3﹣4x,新几何体的体积=x(x+2)(x﹣2),
∴x3﹣4x=x(x+2)(x﹣2).
故答案为:x3﹣4x=x(x+2)(x﹣2).
