第21章 二次函数与反比例函数单元测试题(含答案)
文档属性
| 名称 | 第21章 二次函数与反比例函数单元测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 506.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-10 17:17:42 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025沪科版九年级数学上册
第21章 二次函数与反比例函数
题号 一 二 三 四 五 六 七 八 总分
分数
一、选择题(本大题共10小题,每小题4分,满分40分.每小题有四个选项,其中只有一个选项符合题意)
1.已知反比例函数y=(k≠0),当x=3时,y=10,则k等于 ( )
A. 30 B. C. D. 10
2.函数y=-x2+3与y=-x2-2的图象的不同之处是 ( )
A. 顶点 B. 开口方向 C. 对称轴 D. 形状
3.(2022·上海中考)已知反比例函数y=(k≠0),且在每个象限内,y随x的增大而增大,则下列点可能在这个函数图象上的为 ( )
A. (2,3) B. (-2,3) C. (3,0) D. (-3,0)
4.(2023·安徽省蚌埠禹会区期中)若y=(m-2)是关于x的二次函数,则m的值为 ( )
A. ±2 B. 2 C. -2 D. ±
5.(2022·浙江温州鹿城区期中)抛物线y=x2+4x+4与x轴的交点个数为 ( )
A. 0 B. 3 C. 2 D. 1
6.(2023·山东淄博张店区期中)若正比例函数y=-2x与反比例函数y=的图象交于点(1,-2),则另一个交点坐标为 ( )
A. (2,1) B. (-1,2) C. (-2,-1) D. (-2,1)
7.[课标新增|二次函数和一元二次方程的关系]若二次函数y=ax2-1的图象经过点(-2,0),则关于x的方程a(x-2)2-1=0的根为 ( )
A. x1=0,x2=4 B. x1=-2,x2=6 C. x1=,x2= D. x1=-4,x2=0
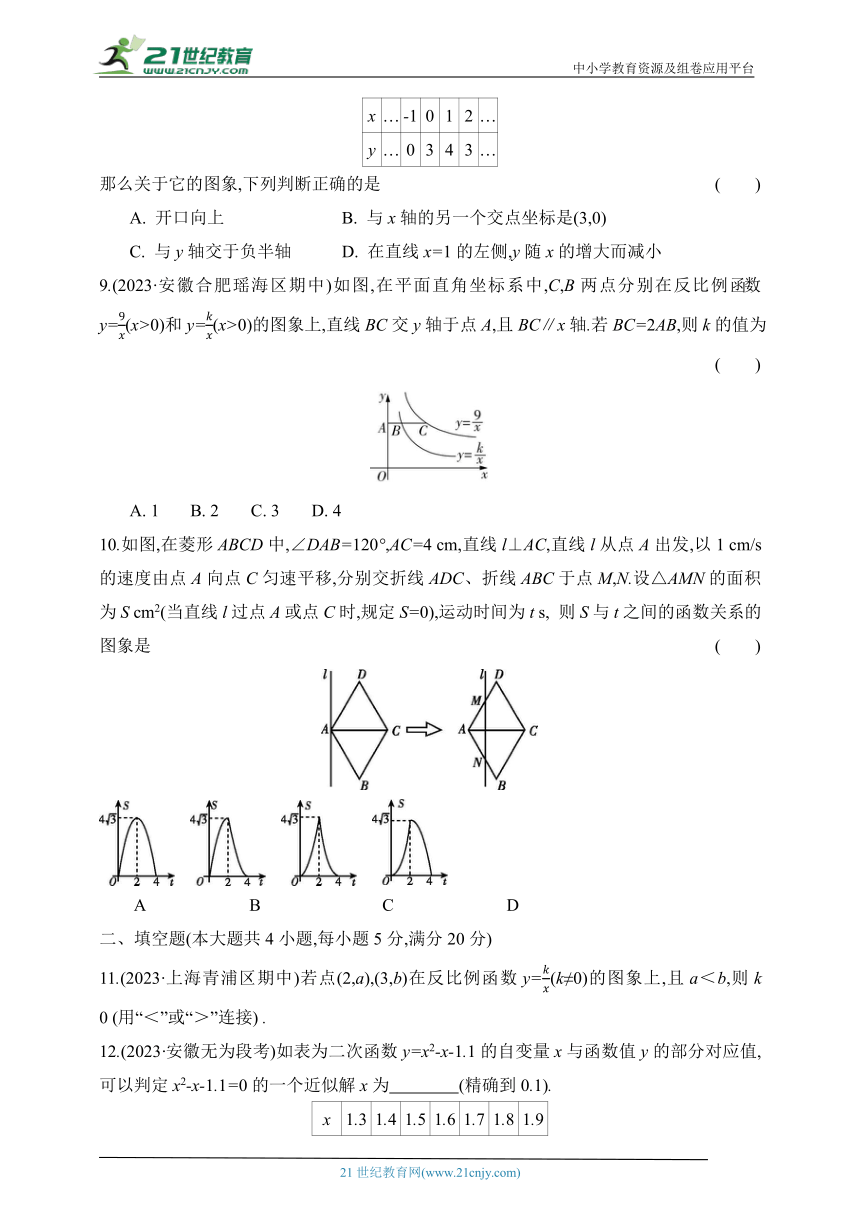
8.(2022·江苏南京鼓楼区期中)已知二次函数y=ax2+bx+c(a≠0)的图象上部分点的横坐标x与纵坐标y的对应值如表:
x … -1 0 1 2 …
y … 0 3 4 3 …
那么关于它的图象,下列判断正确的是 ( )
A. 开口向上 B. 与x轴的另一个交点坐标是(3,0)
C. 与y轴交于负半轴 D. 在直线x=1的左侧,y随x的增大而减小
9.(2023·安徽合肥瑶海区期中)如图,在平面直角坐标系中,C,B两点分别在反比例函数y=(x>0)和y=(x>0)的图象上,直线BC交y轴于点A,且BC∥x轴.若BC=2AB,则k的值为 ( )
A. 1 B. 2 C. 3 D. 4
10.如图,在菱形ABCD中,∠DAB=120°,AC=4 cm,直线l⊥AC,直线l从点A出发,以1 cm/s的速度由点A向点C匀速平移,分别交折线ADC、折线ABC于点M,N.设△AMN的面积为S cm2(当直线l过点A或点C时,规定S=0),运动时间为t s, 则S与t之间的函数关系的图象是 ( )
A B C D
二、填空题(本大题共4小题,每小题5分,满分20分)
11.(2023·上海青浦区期中)若点(2,a),(3,b)在反比例函数y=(k≠0)的图象上,且a<b,则k 0 (用“<”或“>”连接) .
12.(2023·安徽无为段考)如表为二次函数y=x2-x-1.1的自变量x与函数值y的部分对应值,可以判定x2-x-1.1=0的一个近似解x为 (精确到0.1).
x 1.3 1.4 1.5 1.6 1.7 1.8 1.9
y -0.71 -0.54 -0.35 -0.14 0.09 0.34 0.61
13.[课标理念|跨物理学科](2023·湖北武汉洪山区期中)某种小型无人机着陆后滑行的距离y(单位:m)关于滑行的时间t(单位:s)的函数表达式是y=10t-0.25t2,则无人机着陆后滑行 s才能停下来.
14.(2023·安徽安庆迎江区期中)已知抛物线y=ax2+bx-a与y轴交于点A,将点A向右平移2个单位长度得到点B,点B在抛物线上.
(1)此抛物线的对称轴是直线 .
(2)已知点P(,-a),Q(2,2),若抛物线与线段PQ恰有一个交点,则a的取值范围是 .
三、(本大题共2小题,每小题8分,满分16分)
15.(2022·安徽天长市实验中学月考)已知反比例函数y=(m为常数且m≠8).
(1)若函数图象经过点A(-1,6),求m的值;
(2)若函数图象在第二、四象限,求m的取值范围.
16.(2023·安徽合肥四十八中月考)一个二次函数,其图象由抛物线y=x2向右平移1个单位长度所得.
(1)写出平移后的抛物线的函数表达式;
(2)若将(1)中的抛物线再向上平移k(k>0)个单位长度后经过点(2,1),求k的值.
四、(本大题共2小题,每小题8分,满分16分)
17.已知二次函数y=x2-2kx-1.
(1)求证:无论k取何值,该二次函数的图象与x轴都有两个交点.
(2)若该二次函数图象的对称轴为直线x=1,求它的表达式.
18.[课标理念|跨物理学科](2023·河北邢台期末)如图,小明想要用撬棍撬动一块大石头,已知阻力为1 200 N,阻力臂长为0.5 m.设动力为y(单位:N),动力臂长为x(单位:m)(杠杆平衡时,动力×动力臂=阻力×阻力臂,撬棍本身所受的重力忽略不计).
(1)求y关于x的函数表达式.
(2)小明想使动力不超过300 N,在动力臂最大为1.8 m的条件下,他能否撬动这块石头 请说明理由.
五、(本大题共2小题,每小题10分,满分20分)
19.(2023·安徽合肥瑶海区期中)如图,直线y=-x+2与双曲线y=相交于A,B两点,与y轴交于点C,AD⊥x轴,垂足为点D,已知S△ACD=.
(1)求此双曲线的函数表达式;
(2)求点A,B的坐标;
(3)直接写出不等式-x+2>的解集.
20.某河上有一座抛物线形拱桥,当水面离拱顶5 m时,水面AB宽8 m.一木船宽4 m,高2 m,载货后,木船露出水面的部分为 m.以拱顶O为原点建立如图所示的平面直角坐标系,求解下列问题.
(1)点B的坐标为 .
(2)当水面离拱顶1.8 m时,木船能否通过拱桥
六、(本题满分12分)
21.对于实数a,b,我们可以用min{a,b}表示a,b两数中较小的数,例如min{3,-1}=-1,min{2,2}=2. 类似地,若函数y1,y2都是关于x的函数,则y=min{y1, y2}表示函数y1和y2的“取小函数”.
(1)设y1=x,y2=,则函数y=min{x,}的图象应该是 中的实线部分.
A B C D
(2)请在下图中用粗实线描出函数y=min{(x-2)2, (x+2)2}的图象,并写出所描图象的三条不同的性质.
七、(本题满分12分)
22.[课标理念|贴近生活](2023·安徽六安金安区段考)某校增设拓展课程之“开心农场”.如图,利用一堵“L”形墙面(粗线A—B—C表示墙面,已知AB⊥BC,AB=3米,BC=1米)和总长为11米的篱笆围建一个“日”字形的农场DBEF(细线表示篱笆,农场中间用篱笆隔开),点D可能在线段AB上[如图(1)],也可能在线段BA的延长线上[如图(2)],点E在线段BC的延长线上.设DF的长为x米.
(1)当点D在线段AB上时.
①x的取值范围是 .
②若围成的农场DBEF的面积为9米2,求DF的长.
(2)DF的长为多少米时,农场DBEF的面积最大 最大面积为多少平方米
图(1) 图(2)
八、(本题满分14分)
23.如图,若抛物线y=x2+bx+c与x轴相交于A,B两点,与y轴相交于点C,直线y=x-3经过点B, C.
(1)求二次函数的表达式.
(2)点P是直线BC下方抛物线上一动点,过点P作PH⊥x轴于点H,交BC于点M,连接P C.
①线段PM是否有最大值 如果有,求出最大值;如果没有,请说明理由.
②在点P运动的过程中,是否存在点M,恰好使△PCM是以PM为腰的等腰三角形 如果存在,请求出点P的坐标;如果不存在,请说明理由.
第21章 二次函数与反比例函数
1 2 3 4 5 6 7 8 9 10
A A B C D B A B C D
11.< 12.1.7
13.20 14.(1)x=1 (2)-21.A
2.A 对比函数y=-x2+3与y=-x2-2可知,两者的二次项系数相同,一次项系数均为0,所以两抛物线的开口方向相同、形状相同,对称轴也相同.因为抛物线y=-x2+3的顶点坐标为(0,3),而抛物线y=-x2-2的顶点坐标为(0,-2),所以两者的顶点不同.故选A.
3.B 解法一 因为反比例函数y=(k≠0)在每个象限内,y随x的增大而增大,所以k<0.只有B选项中,k=-2×3=-6<0,符合题意.
解法二 根据反比例函数的图象和性质可得,该函数图象在第二象限和第四象限,故选B.
4.C ∵y=(m-2)是关于x的二次函数,∴m2-2=2,且m-2≠0,∴m=-2.
5.D 令x2+4x+4=0.∵Δ=b2-4ac=42-4×1×4=0,∴抛物线y=x2+4x+4与x轴的交点个数为1.
6.B ∵正比例函数与反比例函数的图象均关于原点对称,∴两函数图象的交点关于原点对称.∵一个交点的坐标是(1,-2),∴另一个交点的坐标是(-1,2).
7.A 解法一 把(-2,0)代入二次函数表达式y=ax2-1,得4a-1=0,解得a=,所以方程为(x-2)2-1=0,解得x1=0,x2=4.故选A.
解法二 (整体思想)因为函数y=ax2-1的图象经过点(-2,0),所以根据二次函数的图象的对称性,可得该图象也经过点(2,0),所以ax2-1=0的根为-2或2,所以关于x的方程a(x-2)2-1=0的根为x1=-2+2=0,x2=2+2=4.
8.B 由题中表格知,抛物线的顶点坐标是(1,4),故可设抛物线对应的函数表达式为y=a(x-1)2+4(a≠0).将(-1,0)代入,得a(-1-1)2+4=0,解得a=-1.∵a=-1<0,∴抛物线的开口向下,故选项A错误;抛物线与x轴的一个交点坐标为(-1,0),对称轴是直线x=1,则抛物线与x轴的另一个交点坐标是(3,0),故选项B正确;抛物线与y轴的交点坐标是(0,3),即与y轴交于正半轴,故选项C错误;抛物线的开口向下,对称轴为直线x=1,则在直线x=1的左侧,y随x的增大而增大,故选项D错误.故选B.
9.C 如图,作BM⊥x轴于点M,CN⊥x轴于点N,则S矩形AONC=9,S矩形AOMB=k.∵BC=2AB,∴AC=3AB,∴S矩形AOMB=3,∴k=3.
10.D 当0≤t≤2时,由∠DAB=120°,易得MN=2t,∴S△AMN=MN·t=×2t2=t2,此时函数图象是开口向上的抛物线的一段;当211.< ∵当0<2<3时,a12.1.7 由表可知,当x=1.7时,y的值最接近0,所以方程x2-x-1.1=0的一个近似解x为1.7.
13.20 y=10t-0.25t2=-0.25(t-20)2+100,当t=20时, y取得最大值,即无人机着陆后滑行20 s才能停下来.
14.(1)x=1 (2)-20时,如图(1).当x=2时,y=-a<2;当y=-a时,x=0或x=2.抛物线与线段PQ无交点.②当a<0时,如图(2).当x=2时,y=-a;当x=时,y=-a.∵a<0,∴-a>-a.要使抛物线与线段PQ恰有一个交点,则需满足yQ>yB,即2>-a,解得a>-2.又a<0,∴a的取值范围是-2图(1) 图(2)
15.【参考答案】(1)∵函数图象经过点A(-1,6),
∴m-8=-1×6=-6,
解得m=2. (4分)
(2)∵函数图象在第二、四象限,
∴m-8<0,
解得m<8,
∴m的取值范围是m<8. (8分)
16.【参考答案】(1)由题意可得,向右平移1个单位长度后的抛物线的函数表达式为y=(x-1)2. (4分)
(2)由抛物线y=(x-1)2,再向上平移k个单位长度,
得新的抛物线y=(x-1)2+k.
∵向上平移后的抛物线经过点(2,1),
∴(2-1)2+k=1,解得k=. (8分)
17.【参考答案】(1)证明:令x2-2kx-1=0,
则Δ=b2-4ac=4k2+4>0,
∴关于x的一元二次方程x2-2kx-1=0有两个不相等的实数根,
∴无论k取何值,此二次函数的图象与x轴都有两个交点. (4分)
(2)∵该二次函数图象的对称轴为直线x=1,
∴-=1,解得k=1,
∴二次函数的表达式是y=x2-2x-1. (8分)
18.【参考答案】(1)由题意可得xy=1 200×0.5,
则y=,
即y关于x的函数表达式为y=. (4分)
(2)他不能撬动这块石头.理由如下: (5分)
由(1)知y=,
当y≤300时,
≤300,
解得x≥2.
∵2>1.8,
∴他不能撬动这块石头. (8分)
19.【参考答案】(1)如图,连接OA.
∵AD⊥x轴,
∴S△AOD=S△ACD=,S△AOD=|k|,
∴|k|=3,∴k=-3或3.
∵反比例函数y=的图象在第二、四象限,
∴k<0,∴k=-3,
∴这个双曲线的函数表达式为y=-. (4分)
(2)由题意得
解得或
∴点A(3,-1),B(-1,3). (8分)
(3)不等式-x+2>的解集为x<-1或020.【参考答案】(1)(4,-5) (3分)
(2)设抛物线的函数表达式为y=ax2(a≠0).
将点B的坐标代入y=ax2,得-5=a×42,
解得a=-,
∴该抛物线的函数表达式为y=-x2. (6分)
将x=2代入y=-x2,得y=-.
∵|-|+=2,1.8<2,
∴当水面离拱顶1.8 m时,木船不能通过拱桥. (10分)
21.【参考答案】(1)B(4分)
(2)图象如图所示.
(9分)
所描函数图象的性质有:
对称轴为y轴;
当x<-2时,y随x的增大而减小;
函数的最小值为0.
(答案不唯一) (12分)
22.解题思路:
【参考答案】(1)①3≤x<4 (2分)
解法提示:EF=11-2x-(x-1)=12-3x.
∵AB=3,
∴EF≤3,即12-3x≤3,
解得x≥3.
又EF>0,即12-3x>0,
解得x<4.
综上,x的取值范围是3≤x<4.
②根据题意得x(12-3x)=9,
解得x1=3,x2=1.
由①知x≥3,
∴x2=1不符合题意,
∴DF的长为3米. (6分)
(2)设农场DBEF的面积为S米2.
点D在线段AB上,如题图(1),由(1)知此时3≤x<4,
S=x(12-3x)=-3x2+12x=-3(x-2)2+12.
∵a=-3<0,抛物线开口向下,对称轴是直线x=2,
∴在对称轴右侧,S随x的增大而减小,
∴当x=3时,S有最大值,S最大值=-3×12+12=9.
点D在线段BA的延长线上,如题图(2),此时x<3,
EF==-x,
S=x(-x)=-(x-)2+.
∵a=-<0,<3,
∴当x=时,S有最大值,S最大值=.
∵>9,
∴DF的长为米时,农场DBEF的面积最大,最大面积为米2. (12分)
23. 【参考答案】(1)∵直线y=x-3经过点B,C,当x=0时,y=-3;当y=0时,x=3,∴B(3,0),C(0,-3).
将B,C两点的坐标代入y=x2+bx+c,
得解得
故二次函数的表达式为y=x2-2x-3. (4分)
(2)设M(x,x-3),则P(x,x2-2x-3).
①线段PM有最大值.
PM=(x-3)-(x2-2x-3)=-(x-)2+. (6分)
∵-1<0,∴PM有最大值.
当x=时,PM最大为. (9分)
②存在. (10分)
PM2=(x-3-x2+2x+3)2=(-x2+3x)2,
PC2=x2+(-3-x2+2x+3)2=x2+(2x-x2)2,
MC2=(x-3+3)2+x2=2x2.
当PM=PC时,(-x2+3x)2=x2+(2x-x2)2,
解得x1=2,x2=0(舍去),
∴P(2,-3). (12分)
当MP=MC时,(-x2+3x)2=2x2,
解得x1=3-,x2=0(舍去),x3=3+(舍去),
∴P(3-,2-4).
综上,点P的坐标为(2,-3)或(3-,2-4). (14分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025沪科版九年级数学上册
第21章 二次函数与反比例函数
题号 一 二 三 四 五 六 七 八 总分
分数
一、选择题(本大题共10小题,每小题4分,满分40分.每小题有四个选项,其中只有一个选项符合题意)
1.已知反比例函数y=(k≠0),当x=3时,y=10,则k等于 ( )
A. 30 B. C. D. 10
2.函数y=-x2+3与y=-x2-2的图象的不同之处是 ( )
A. 顶点 B. 开口方向 C. 对称轴 D. 形状
3.(2022·上海中考)已知反比例函数y=(k≠0),且在每个象限内,y随x的增大而增大,则下列点可能在这个函数图象上的为 ( )
A. (2,3) B. (-2,3) C. (3,0) D. (-3,0)
4.(2023·安徽省蚌埠禹会区期中)若y=(m-2)是关于x的二次函数,则m的值为 ( )
A. ±2 B. 2 C. -2 D. ±
5.(2022·浙江温州鹿城区期中)抛物线y=x2+4x+4与x轴的交点个数为 ( )
A. 0 B. 3 C. 2 D. 1
6.(2023·山东淄博张店区期中)若正比例函数y=-2x与反比例函数y=的图象交于点(1,-2),则另一个交点坐标为 ( )
A. (2,1) B. (-1,2) C. (-2,-1) D. (-2,1)
7.[课标新增|二次函数和一元二次方程的关系]若二次函数y=ax2-1的图象经过点(-2,0),则关于x的方程a(x-2)2-1=0的根为 ( )
A. x1=0,x2=4 B. x1=-2,x2=6 C. x1=,x2= D. x1=-4,x2=0
8.(2022·江苏南京鼓楼区期中)已知二次函数y=ax2+bx+c(a≠0)的图象上部分点的横坐标x与纵坐标y的对应值如表:
x … -1 0 1 2 …
y … 0 3 4 3 …
那么关于它的图象,下列判断正确的是 ( )
A. 开口向上 B. 与x轴的另一个交点坐标是(3,0)
C. 与y轴交于负半轴 D. 在直线x=1的左侧,y随x的增大而减小
9.(2023·安徽合肥瑶海区期中)如图,在平面直角坐标系中,C,B两点分别在反比例函数y=(x>0)和y=(x>0)的图象上,直线BC交y轴于点A,且BC∥x轴.若BC=2AB,则k的值为 ( )
A. 1 B. 2 C. 3 D. 4
10.如图,在菱形ABCD中,∠DAB=120°,AC=4 cm,直线l⊥AC,直线l从点A出发,以1 cm/s的速度由点A向点C匀速平移,分别交折线ADC、折线ABC于点M,N.设△AMN的面积为S cm2(当直线l过点A或点C时,规定S=0),运动时间为t s, 则S与t之间的函数关系的图象是 ( )
A B C D
二、填空题(本大题共4小题,每小题5分,满分20分)
11.(2023·上海青浦区期中)若点(2,a),(3,b)在反比例函数y=(k≠0)的图象上,且a<b,则k 0 (用“<”或“>”连接) .
12.(2023·安徽无为段考)如表为二次函数y=x2-x-1.1的自变量x与函数值y的部分对应值,可以判定x2-x-1.1=0的一个近似解x为 (精确到0.1).
x 1.3 1.4 1.5 1.6 1.7 1.8 1.9
y -0.71 -0.54 -0.35 -0.14 0.09 0.34 0.61
13.[课标理念|跨物理学科](2023·湖北武汉洪山区期中)某种小型无人机着陆后滑行的距离y(单位:m)关于滑行的时间t(单位:s)的函数表达式是y=10t-0.25t2,则无人机着陆后滑行 s才能停下来.
14.(2023·安徽安庆迎江区期中)已知抛物线y=ax2+bx-a与y轴交于点A,将点A向右平移2个单位长度得到点B,点B在抛物线上.
(1)此抛物线的对称轴是直线 .
(2)已知点P(,-a),Q(2,2),若抛物线与线段PQ恰有一个交点,则a的取值范围是 .
三、(本大题共2小题,每小题8分,满分16分)
15.(2022·安徽天长市实验中学月考)已知反比例函数y=(m为常数且m≠8).
(1)若函数图象经过点A(-1,6),求m的值;
(2)若函数图象在第二、四象限,求m的取值范围.
16.(2023·安徽合肥四十八中月考)一个二次函数,其图象由抛物线y=x2向右平移1个单位长度所得.
(1)写出平移后的抛物线的函数表达式;
(2)若将(1)中的抛物线再向上平移k(k>0)个单位长度后经过点(2,1),求k的值.
四、(本大题共2小题,每小题8分,满分16分)
17.已知二次函数y=x2-2kx-1.
(1)求证:无论k取何值,该二次函数的图象与x轴都有两个交点.
(2)若该二次函数图象的对称轴为直线x=1,求它的表达式.
18.[课标理念|跨物理学科](2023·河北邢台期末)如图,小明想要用撬棍撬动一块大石头,已知阻力为1 200 N,阻力臂长为0.5 m.设动力为y(单位:N),动力臂长为x(单位:m)(杠杆平衡时,动力×动力臂=阻力×阻力臂,撬棍本身所受的重力忽略不计).
(1)求y关于x的函数表达式.
(2)小明想使动力不超过300 N,在动力臂最大为1.8 m的条件下,他能否撬动这块石头 请说明理由.
五、(本大题共2小题,每小题10分,满分20分)
19.(2023·安徽合肥瑶海区期中)如图,直线y=-x+2与双曲线y=相交于A,B两点,与y轴交于点C,AD⊥x轴,垂足为点D,已知S△ACD=.
(1)求此双曲线的函数表达式;
(2)求点A,B的坐标;
(3)直接写出不等式-x+2>的解集.
20.某河上有一座抛物线形拱桥,当水面离拱顶5 m时,水面AB宽8 m.一木船宽4 m,高2 m,载货后,木船露出水面的部分为 m.以拱顶O为原点建立如图所示的平面直角坐标系,求解下列问题.
(1)点B的坐标为 .
(2)当水面离拱顶1.8 m时,木船能否通过拱桥
六、(本题满分12分)
21.对于实数a,b,我们可以用min{a,b}表示a,b两数中较小的数,例如min{3,-1}=-1,min{2,2}=2. 类似地,若函数y1,y2都是关于x的函数,则y=min{y1, y2}表示函数y1和y2的“取小函数”.
(1)设y1=x,y2=,则函数y=min{x,}的图象应该是 中的实线部分.
A B C D
(2)请在下图中用粗实线描出函数y=min{(x-2)2, (x+2)2}的图象,并写出所描图象的三条不同的性质.
七、(本题满分12分)
22.[课标理念|贴近生活](2023·安徽六安金安区段考)某校增设拓展课程之“开心农场”.如图,利用一堵“L”形墙面(粗线A—B—C表示墙面,已知AB⊥BC,AB=3米,BC=1米)和总长为11米的篱笆围建一个“日”字形的农场DBEF(细线表示篱笆,农场中间用篱笆隔开),点D可能在线段AB上[如图(1)],也可能在线段BA的延长线上[如图(2)],点E在线段BC的延长线上.设DF的长为x米.
(1)当点D在线段AB上时.
①x的取值范围是 .
②若围成的农场DBEF的面积为9米2,求DF的长.
(2)DF的长为多少米时,农场DBEF的面积最大 最大面积为多少平方米
图(1) 图(2)
八、(本题满分14分)
23.如图,若抛物线y=x2+bx+c与x轴相交于A,B两点,与y轴相交于点C,直线y=x-3经过点B, C.
(1)求二次函数的表达式.
(2)点P是直线BC下方抛物线上一动点,过点P作PH⊥x轴于点H,交BC于点M,连接P C.
①线段PM是否有最大值 如果有,求出最大值;如果没有,请说明理由.
②在点P运动的过程中,是否存在点M,恰好使△PCM是以PM为腰的等腰三角形 如果存在,请求出点P的坐标;如果不存在,请说明理由.
第21章 二次函数与反比例函数
1 2 3 4 5 6 7 8 9 10
A A B C D B A B C D
11.< 12.1.7
13.20 14.(1)x=1 (2)-2
2.A 对比函数y=-x2+3与y=-x2-2可知,两者的二次项系数相同,一次项系数均为0,所以两抛物线的开口方向相同、形状相同,对称轴也相同.因为抛物线y=-x2+3的顶点坐标为(0,3),而抛物线y=-x2-2的顶点坐标为(0,-2),所以两者的顶点不同.故选A.
3.B 解法一 因为反比例函数y=(k≠0)在每个象限内,y随x的增大而增大,所以k<0.只有B选项中,k=-2×3=-6<0,符合题意.
解法二 根据反比例函数的图象和性质可得,该函数图象在第二象限和第四象限,故选B.
4.C ∵y=(m-2)是关于x的二次函数,∴m2-2=2,且m-2≠0,∴m=-2.
5.D 令x2+4x+4=0.∵Δ=b2-4ac=42-4×1×4=0,∴抛物线y=x2+4x+4与x轴的交点个数为1.
6.B ∵正比例函数与反比例函数的图象均关于原点对称,∴两函数图象的交点关于原点对称.∵一个交点的坐标是(1,-2),∴另一个交点的坐标是(-1,2).
7.A 解法一 把(-2,0)代入二次函数表达式y=ax2-1,得4a-1=0,解得a=,所以方程为(x-2)2-1=0,解得x1=0,x2=4.故选A.
解法二 (整体思想)因为函数y=ax2-1的图象经过点(-2,0),所以根据二次函数的图象的对称性,可得该图象也经过点(2,0),所以ax2-1=0的根为-2或2,所以关于x的方程a(x-2)2-1=0的根为x1=-2+2=0,x2=2+2=4.
8.B 由题中表格知,抛物线的顶点坐标是(1,4),故可设抛物线对应的函数表达式为y=a(x-1)2+4(a≠0).将(-1,0)代入,得a(-1-1)2+4=0,解得a=-1.∵a=-1<0,∴抛物线的开口向下,故选项A错误;抛物线与x轴的一个交点坐标为(-1,0),对称轴是直线x=1,则抛物线与x轴的另一个交点坐标是(3,0),故选项B正确;抛物线与y轴的交点坐标是(0,3),即与y轴交于正半轴,故选项C错误;抛物线的开口向下,对称轴为直线x=1,则在直线x=1的左侧,y随x的增大而增大,故选项D错误.故选B.
9.C 如图,作BM⊥x轴于点M,CN⊥x轴于点N,则S矩形AONC=9,S矩形AOMB=k.∵BC=2AB,∴AC=3AB,∴S矩形AOMB=3,∴k=3.
10.D 当0≤t≤2时,由∠DAB=120°,易得MN=2t,∴S△AMN=MN·t=×2t2=t2,此时函数图象是开口向上的抛物线的一段;当2
13.20 y=10t-0.25t2=-0.25(t-20)2+100,当t=20时, y取得最大值,即无人机着陆后滑行20 s才能停下来.
14.(1)x=1 (2)-2
15.【参考答案】(1)∵函数图象经过点A(-1,6),
∴m-8=-1×6=-6,
解得m=2. (4分)
(2)∵函数图象在第二、四象限,
∴m-8<0,
解得m<8,
∴m的取值范围是m<8. (8分)
16.【参考答案】(1)由题意可得,向右平移1个单位长度后的抛物线的函数表达式为y=(x-1)2. (4分)
(2)由抛物线y=(x-1)2,再向上平移k个单位长度,
得新的抛物线y=(x-1)2+k.
∵向上平移后的抛物线经过点(2,1),
∴(2-1)2+k=1,解得k=. (8分)
17.【参考答案】(1)证明:令x2-2kx-1=0,
则Δ=b2-4ac=4k2+4>0,
∴关于x的一元二次方程x2-2kx-1=0有两个不相等的实数根,
∴无论k取何值,此二次函数的图象与x轴都有两个交点. (4分)
(2)∵该二次函数图象的对称轴为直线x=1,
∴-=1,解得k=1,
∴二次函数的表达式是y=x2-2x-1. (8分)
18.【参考答案】(1)由题意可得xy=1 200×0.5,
则y=,
即y关于x的函数表达式为y=. (4分)
(2)他不能撬动这块石头.理由如下: (5分)
由(1)知y=,
当y≤300时,
≤300,
解得x≥2.
∵2>1.8,
∴他不能撬动这块石头. (8分)
19.【参考答案】(1)如图,连接OA.
∵AD⊥x轴,
∴S△AOD=S△ACD=,S△AOD=|k|,
∴|k|=3,∴k=-3或3.
∵反比例函数y=的图象在第二、四象限,
∴k<0,∴k=-3,
∴这个双曲线的函数表达式为y=-. (4分)
(2)由题意得
解得或
∴点A(3,-1),B(-1,3). (8分)
(3)不等式-x+2>的解集为x<-1或0
(2)设抛物线的函数表达式为y=ax2(a≠0).
将点B的坐标代入y=ax2,得-5=a×42,
解得a=-,
∴该抛物线的函数表达式为y=-x2. (6分)
将x=2代入y=-x2,得y=-.
∵|-|+=2,1.8<2,
∴当水面离拱顶1.8 m时,木船不能通过拱桥. (10分)
21.【参考答案】(1)B(4分)
(2)图象如图所示.
(9分)
所描函数图象的性质有:
对称轴为y轴;
当x<-2时,y随x的增大而减小;
函数的最小值为0.
(答案不唯一) (12分)
22.解题思路:
【参考答案】(1)①3≤x<4 (2分)
解法提示:EF=11-2x-(x-1)=12-3x.
∵AB=3,
∴EF≤3,即12-3x≤3,
解得x≥3.
又EF>0,即12-3x>0,
解得x<4.
综上,x的取值范围是3≤x<4.
②根据题意得x(12-3x)=9,
解得x1=3,x2=1.
由①知x≥3,
∴x2=1不符合题意,
∴DF的长为3米. (6分)
(2)设农场DBEF的面积为S米2.
点D在线段AB上,如题图(1),由(1)知此时3≤x<4,
S=x(12-3x)=-3x2+12x=-3(x-2)2+12.
∵a=-3<0,抛物线开口向下,对称轴是直线x=2,
∴在对称轴右侧,S随x的增大而减小,
∴当x=3时,S有最大值,S最大值=-3×12+12=9.
点D在线段BA的延长线上,如题图(2),此时x<3,
EF==-x,
S=x(-x)=-(x-)2+.
∵a=-<0,<3,
∴当x=时,S有最大值,S最大值=.
∵>9,
∴DF的长为米时,农场DBEF的面积最大,最大面积为米2. (12分)
23. 【参考答案】(1)∵直线y=x-3经过点B,C,当x=0时,y=-3;当y=0时,x=3,∴B(3,0),C(0,-3).
将B,C两点的坐标代入y=x2+bx+c,
得解得
故二次函数的表达式为y=x2-2x-3. (4分)
(2)设M(x,x-3),则P(x,x2-2x-3).
①线段PM有最大值.
PM=(x-3)-(x2-2x-3)=-(x-)2+. (6分)
∵-1<0,∴PM有最大值.
当x=时,PM最大为. (9分)
②存在. (10分)
PM2=(x-3-x2+2x+3)2=(-x2+3x)2,
PC2=x2+(-3-x2+2x+3)2=x2+(2x-x2)2,
MC2=(x-3+3)2+x2=2x2.
当PM=PC时,(-x2+3x)2=x2+(2x-x2)2,
解得x1=2,x2=0(舍去),
∴P(2,-3). (12分)
当MP=MC时,(-x2+3x)2=2x2,
解得x1=3-,x2=0(舍去),x3=3+(舍去),
∴P(3-,2-4).
综上,点P的坐标为(2,-3)或(3-,2-4). (14分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
