第22章 相似形单元测试题(含答案)
文档属性
| 名称 | 第22章 相似形单元测试题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 580.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-10 17:20:36 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025沪科版九年级数学上册
第22章 相似形
题号 一 二 三 四 五 六 七 八 总分
分数
一、选择题(本大题共10小题,每小题4分,满分40分.每小题有四个选项,其中只有一个选项符合题意)
1.(2023·陕西西安爱知中学月考)已知四条线段a,b,c,d是成比例线段,其中b=3 cm,c=4 cm,d=6 cm,则线段a的长度为 ( )
A. 8 cm B. 2 cm C. 4 cm D. 1 cm
2.(2023·上海宝山区期中)下列各组图形,一定相似的是 ( )
A. 两个等腰梯形 B. 两个菱形 C. 两个正方形 D. 两个矩形
3.(2022·湖南怀化期末)已知△ABC∽△DEF,若∠A=30°,∠E=50°,则∠F的度数为 ( )
A. 110° B. 100° C. 90° D. 80°
4.[课标理念|结合真实情境](2022·浙江丽水中考)如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段AB=3,则线段BC的长是( )
A. B. 1 C. D. 2
(第4题) (第5题) (第6题)
5.(2023·浙江杭州江干区期中)如图,在△ABC中,∠C=90°,∠A=30°,D是AC的中点,若过点D沿直线剪下一个与△ABC相似的小三角形,则不同的剪法共有 ( )
A. 3种 B. 2种 C. 1种 D. 4种
6.(2023·安徽宣城宣化区期末)如图,F为 ABCD的边AD上一点,射线BF交CD的延长线于点E,则下列结论正确的是 ( )
A. = B. = C. = D. =
7.在平面直角坐标系中,矩形OABC的顶点O为原点,边OA在x轴的正半轴上,边OC在y轴的正半轴上,点B的坐标是(6,4).如果矩形OA'B'C'与矩形OABC关于点O位似,且矩形OA'B'C'的面积等于矩形OABC的面积的,那么点B'的坐标是 ( )
A. (3,2) B. (-2,-3) C. (3,2)或(-3,-2) D. (2,3)或(-2,-3)
8.如图,在正方形ABCD中,E为AB的中点,G,F分别为AD,BC边上的点.若AG=1,BF=2,∠GEF=90°,则GF的长为 ( )
A. 2 B. 3 C. 4 D. 5
(第8题) (第9题)
9.如图,在菱形ABCD中,∠A=60°,点E为边AD上一点,连接BE,CE,其中CE交对角线BD于点F.若AB=2,AE=DF,则AE等于 ( )
A. 3± B. 3- C. D.
10.(2022·浙江诸暨模拟)如图,将一张面积为50的大三角形纸片沿着虚线剪成三张小三角形纸片与一张矩形纸片.根据图中标出的长度,则矩形纸片的面积为 ( )
A. 12 B. 18 C. 24 D. 30
二、填空题(本大题共4小题,每小题5分,满分20分)
11.[中考创新题型|开放性试题](2023·北京通州区期中)如图,在△ABC中,AB=AC,点D在AC上(不与点A,C重合),只需添加一个条件即可证明△ABC和△BDC相似,这个条件可以是 (写出一个即可).
(第11题) (第13题) (第14题)
12.(2022·四川成都锦江区段考)已知△ABC与△DEF的相似比为3∶5.若它们周长差是24,则△DEF的周长为 .
13.[课标理念|关注数学文化](2022·北京东城区二模)据《墨经》记载,在两千多年前,我国墨子和他的学生做了世界上第一个“小孔成像”的实验,阐释了光的直线传播原理,如图(1)所示.在如图(2)所示的小孔成像实验中,若物距为10 cm,像距为15 cm,蜡烛火焰倒立的像的高度是6 cm,则蜡烛火焰的高度是 cm.
14.(2022·安徽合肥五十中月考)如图,在正方形ABCD中,AB=4,M为BC的中点,点N在射线AD上,过点N作NE⊥AM于点E,连接MN,则:
(1)= ;
(2)当△MEN与△ABM相似时,AN= .
三、(本大题共2小题,每小题8分,满分16分)
15.(2022·安徽合肥期中)如图,BE是△ABC的角平分线,延长BE至点D,使得BC=CD. 求证:△AEB∽△CED.
16.(2023·浙江绍兴柯桥区期中)已知线段a,b,c满足==,且a+2b+c=26.
(1)求线段a,b,c的长;
(2)若线段m是线段a,b的比例中项,求线段m的长.
四、(本大题共2小题,每小题8分,满分16分)
17. (2023·浙江杭州西湖区期中)如图,在Rt△ABC中,∠C=90°,D是AB的中点,DE∥BC,BE⊥AB.
(1)求证:△DEB∽△BAC;
(2)若AB=6,AC=2,求的值.
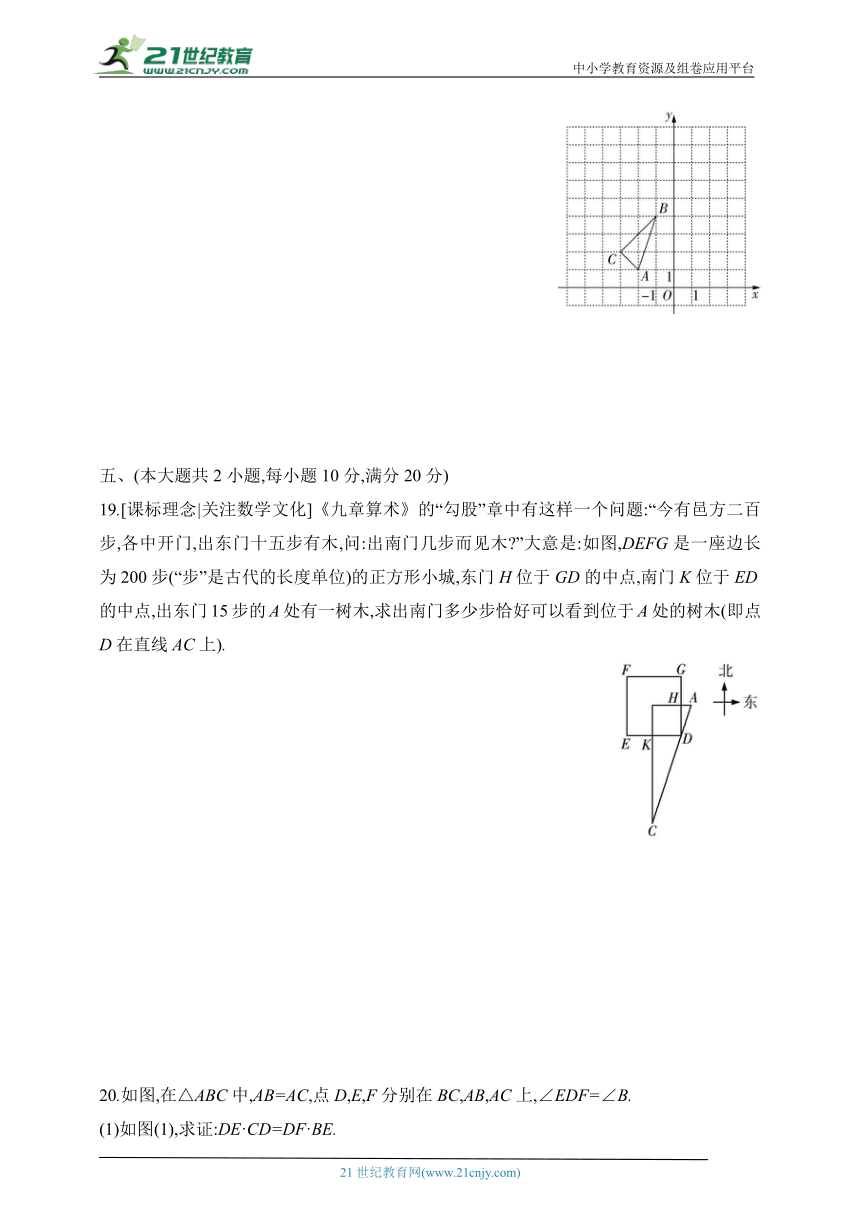
18.(2023·广州深圳福田区期中)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1.
(2)以原点O为位似中心,相似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2.
(3)点C2的坐标为 ;△ABC与△A2B2C2的周长比是 .
五、(本大题共2小题,每小题10分,满分20分)
19.[课标理念|关注数学文化]《九章算术》的“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木 ”大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好可以看到位于A处的树木(即点D在直线AC上).
20.如图,在△ABC中,AB=AC,点D,E,F分别在BC,AB,AC上,∠EDF=∠B.
(1)如图(1),求证:DE·CD=DF·BE.
(2)若D为BC的中点,如图(2),连接EF.求证:ED平分∠BEF.
图(1) 图(2)
六、(本题满分12分)
21.[中考创新题型|综合与实践题]某数学兴趣小组为了测量校内路灯的灯柱AB的高度,设计了以下三个方案.
方案一:如图(1),在操场上点C处放一面平面镜,从点C处后退1 m到点D处,恰好在平面镜中看到灯柱的顶部A点的像.再将平面镜向后移动4 m(即FC=4 m)放在F处,从点F处向后退1.5 m到点H处,恰好再次在平面镜中看到灯柱的顶部A点的像,其中眼睛距地面的高度ED,GH均为1.5 m,已知点B,C,D,F,H在同一水平线上,且GH⊥FH,ED⊥CD,AB⊥BH(平面镜的大小忽略不计).
方案二:如图(2),利用标杆CD测量灯柱的高度.已知标杆CD高1.5 m,测得DE=2 m,CE=2.5 m.
方案三:如图(3),将直角三角形支架的直角边CE保持水平,并且边CE与点M在同一直线上.已知两条边CE=0.4 m,EF=0.2 m,测得边CE离地面距离DC=1.5 m.
以上三种方案中,方案 不可行,请选择可行的方案,并求出灯柱的高度.
七、(本题满分12分)
22.[中考新题型|阅读理解题]先阅读下面的材料,然后解答问题.
材料:从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的“完美分割线”.例如:如图(1),AD把△ABC分成△ABD与△ADC,若△ABD是等腰三角形,且△ADC∽△BAC,那么AD就是△ABC的“完美分割线”.
解答下列问题:
(1)如图(2),在△ABC中,∠B=40°,AD是△ABC的“完美分割线”,且△ABD是以AD为底边的等腰三角形,则∠CAD= °;
(2)在△ABC中,∠B=42°,AD是△ABC的“完美分割线”,且△ABD是等腰三角形,求∠BAC的度数.
图(1) 图(2)
八、(本题满分14分)
23.(2023·安徽安庆迎江区期中)在△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE,线段AC与DE交于点G,连接BD,CE.
(1)如图(1),当B,D,E三点共线时,求证:∠BEC=∠DAE.
(2)如图(2),当B,D,E三点不共线时,延长ED交BC于点F.
①求证:AD·CG=EG·FC;
②若∠BAC=∠ADB=90°,求 的值.
图(1) 图(2)
第22章 相似形
1 2 3 4 5 6 7 8 9 10
B C B C A B C B B C
11.∠A=∠CBD(答案不唯一,或∠ABC=∠BDC等) 12.60
13.4 14.(1) (2)2或5
1.B ∵四条线段a,b,c,d是成比例线段,∴a∶b=c∶d,即a∶3=4∶6,∴a=2 cm.
2.C 两个正方形,形状相同,大小不一定相同,符合相似形定义,故选C.
3.B ∵△ABC∽△DEF,∴∠D=∠A=30°,∴∠F=180°-∠D-∠E=100°.
4.C 如图,过点A作平行横线的垂线,交点B所在的平行横线于点D,交点C所在的平行横线于点E.由题意可得,=,即=2,解得BC=.
5.A 如图,在AB边上取一点F,连接DF,使DF∥BC,此时易得△ADF∽△ACB;在BC边上取一点G,连接DG,使DG∥AB,此时易得△CDG∽△CAB;在AB边上取一点E,连接DE,使DE⊥AB,此时易得△ADE∽△ABC.故不同的剪法共有3种.
6.B ∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,∴△ABF∽△DEF,△EFD∽△EBC,∴=,=,=,故选项A,C,D错误;∵△ABF∽△DEF,△EFD∽△EBC,∴△ABF∽△CEB,∴=.故选B.
7.C 由题意知,矩形OA'B'C'与矩形OABC的相似比是1∶2.如图,∵点B的坐标是(6,4),∴点B'的坐标是(3,2)或(-3,-2).
8.B ∵四边形ABCD是正方形,∴∠A=∠B=90°,∴∠AGE+∠AEG=90°.∵∠AEG+∠BEF=90°,∴∠AGE=∠BEF,∴△AGE∽△BEF,∴= .
∵E为AB的中点,∴AE=BE.∵AG=1,BF=2,∴=,解得AE=.在Rt△AEG中,GE2=AG2+AE2=3.在Rt△BEF中,EF2=BE2+BF2=6.在Rt△GEF中,GF==3.
9.B ∵四边形ABCD是菱形,∠A=60°,∴△ABD和△CBD都是等边三角形,∴AD=BD=AB=2.∵AD∥BC,∴∠EDF=∠CBF,∠DEF=∠BCF,
∴△DEF∽△BCF,∴=.又AE=DF,∴=,解得AE=3±.由题意可得010.C 如图,过点A作AH⊥BC于点H,交DE于点M,∵△ABC的面积为50,∴×10×AH=50,∴AH=10.∵四边形DFGE是矩形,∴DF=MH=EG,
DE∥BC,∴∠ADE=∠ABC,∠AED=∠ACB,∴△ADE∽△ABC,∴=,即=,∴MH=4,∴DF=4,∴S矩形DFGE=DE·DF=6×4=24.
11.∠A=∠CBD(答案不唯一,或∠ABC=∠BDC等) ∵∠A=∠CBD,∠ACB=∠BCD,∴△ABC∽△BDC.
12.60 ∵△ABC与△DEF的相似比为3∶5,∴△ABC与△DEF的周长比是3∶5.由题意设△ABC的周长为3x,则△DEF的周长为5x,则有5x-3x=24,解得x=12,∴5x=60,∴△DEF的周长为60.
13.4 设蜡烛火焰的高度是x cm,由相似三角形的性质得=,解得x=4,即蜡烛火焰的高度是4 cm.
14.(1) (2)2或5 (1)∵四边形ABCD是正方形,∴AB=BC=AD=4.∵点M是BC的中点,∴BM=CM=2,∴AM===2.
∵BC∥AD,NE⊥AM,∴△ABM∽△NEA,∴==.(2)当∠AMB=∠NME时,则△ABM∽△NEM,∴∠AMB=∠NME=∠MAN,∴AN=MN.∵EN⊥AM,
∴AE=EM=.∵=,∴AN=5.如图,当∠BAM=∠EMN时,△ABM∽△MEN,∴∠MAN+∠AMN=90°,∴∠ANM=90°,∴四边形ABMN是矩形,∴AN=BM=2.综上所述,AN的长为2或5.
15.【参考答案】证明:∵BE是△ABC的角平分线,
∴∠ABE=∠CBE. (2分)
∵BC=CD,
∴∠CBE=∠D, (4分)
∴∠ABE=∠D. (6分)
∵∠AEB=∠CED,
∴△AEB∽△CED. (8分)
16.【参考答案】(1)(设参法)设===k,
则a=3k,b=2k,c=6k.
∵a+2b+c=26,
∴3k+2×2k+6k=26,
解得k=2,
∴a=6,b=4,c=12. (4分)
(2)∵线段m是线段a,b的比例中项,
∴=,即m2=ab=4×6=24,
解得m=2或m=-2(舍去),
∴线段m的长为2. (8分)
17.【解题思路】(1)由DE∥BC得,∠EDB=∠ABC.根据垂直说明∠EBD=∠C=90°,即可得出结论.(2)先由勾股定理求出BC的长,再由相似三角形的面积比等于相似比的平方,即可求得结论.
【参考答案】(1)证明:∵∠C=90°,BE⊥AB,
∴∠EBD=∠C=90°. (2分)
∵DE∥BC,
∴∠EDB=∠ABC,
∴△DEB∽△BAC. (5分)
(2)由勾股定理得BC===4.(6分)
∵D是AB的中点,AB=6,
∴DB=3.
∵△DEB∽△BAC,
∴=()2=()2=. (8分)
18.【参考答案】(1)如图,△A1B1C1为所作. (3分)
(2)如图,△A2B2C2为所作. (6分)
(3)(-6,4) 1∶2 (8分)
19.【参考答案】由题意知DH=DK=100步,AH=15步.
∵AH∥DK,∴∠CDK=∠A.
又∠CKD=∠DHA,∴△CDK∽△DAH, (5分)
∴=,即=,
∴CK=步. (9分)
答:出南门步恰好看到位于A处的树木. (10分)
20.【参考答案】(1)证明:∵AB=AC,∴∠B=∠C.
∵∠B+∠BDE+∠DEB=180°,
∠BDE+∠EDF+∠FDC=180°,
∠EDF=∠B,
∴∠FDC=∠DEB,∴△BDE∽△CFD,
∴=,
即DE·CD=DF·BE. (5分)
(2)证明:由(1)可知=.
∵D为BC的中点,∴BD=CD,
∴=,∴=. (8分)
又∠B=∠EDF,
∴△BDE∽△DFE,
∴∠BED=∠DEF,
∴ED平分∠BEF. (10分)
21.【参考答案】二、三 (2分)
解法提示:根据相似三角形的知识可知,
方案二中△ABE缺少边长的条件,
故方案二不可行.
方案三中△AMC缺少边长的条件,
故方案三不可行.
选择方案一. (4分)
∵∠ECD=∠ACB,∠EDC=∠ABC,
∴△ABC∽△EDC,
∴=,
∴AB==1.5BC. (8分)
设BC=x m,
则AB=1.5x m.
同理可得△ABF∽△GHF,
∴=.
∵AB=1.5x m,BF=BC+CF=(x+4)m,GH=1.5 m,FH=1.5 m,
∴=,
解得x=8,
∴AB=1.5×8=12(m),
即灯柱的高度为12 m. (12分)
22.【参考答案】(1)40 (4分)
解法提示:∵AD是△ABC的“完美分割线”,
∴△DAC∽△ABC,∴∠CAD=∠B=40°.
(2)若BD=AD,∵AD是△ABC的“完美分割线”,
∴△DAC∽△ABC,
∴∠CAD=∠B=42°.
∵AD=BD,
∴∠ABD=∠BAD=42°,
∴∠BAC=∠BAD+∠CAD=84°. (6分)
若AB=BD,则∠BAD=69°=∠BDA.
∵AD是△ABC的“完美分割线”,
∴△DAC∽△ABC,
∴∠CAD=∠B=42°,
∴∠BAC=∠BAD+∠CAD=69°+42°=111°. (9分)
若AB=AD,则∠B=∠ADB=42°.
∵AD是△ABC的“完美分割线”,
∴△DAC∽△ABC,
∴∠CAD=∠B=42°.
∵∠ADB=∠DAC+∠C=42°+∠C≠42°,
∴不符合题意. (11分)
综上所述,∠BAC的度数为84°或111°. (12分)
23.【参考答案】(1)证明:∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠CAE.
又∵AB=AC,AD=AE,
∴△BAD≌△CAE,
∴∠ADB=∠AEC.
当B,D,E三点共线时,∠ADB=∠AED+∠DAE.
又∵∠AEC=∠AED+∠BEC,
∴∠BEC=∠DAE. (5分)
(2)①证明:∵AB=AC,AD=AE,
∴=.
又∠BAC=∠DAE,
∴△BAC∽△DAE,
∴∠AED=∠ACB.
又∠AGE=∠FGC,
∴△AEG∽△FCG,
∴=,即AE·CG=EG·FC.
又AD=AE,
∴AD·CG=EG·FC. (10分)
②如图,连接AF.
由(1)可知,△BAD≌△CAE,
∴∠AEC=∠ADB=90°.
由①知△AEG∽△FCG,
∴=,即=.
又∠AGF=∠EGC,
∴△AGF∽△EGC,
∴∠AFG=∠ACE,
∴∠AFE+∠EFC=∠ECA+∠EAC=180°-∠AEC=90°,
∴∠AFC=90°,
∴FC=AC=AB,
∴=. (14分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025沪科版九年级数学上册
第22章 相似形
题号 一 二 三 四 五 六 七 八 总分
分数
一、选择题(本大题共10小题,每小题4分,满分40分.每小题有四个选项,其中只有一个选项符合题意)
1.(2023·陕西西安爱知中学月考)已知四条线段a,b,c,d是成比例线段,其中b=3 cm,c=4 cm,d=6 cm,则线段a的长度为 ( )
A. 8 cm B. 2 cm C. 4 cm D. 1 cm
2.(2023·上海宝山区期中)下列各组图形,一定相似的是 ( )
A. 两个等腰梯形 B. 两个菱形 C. 两个正方形 D. 两个矩形
3.(2022·湖南怀化期末)已知△ABC∽△DEF,若∠A=30°,∠E=50°,则∠F的度数为 ( )
A. 110° B. 100° C. 90° D. 80°
4.[课标理念|结合真实情境](2022·浙江丽水中考)如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段AB=3,则线段BC的长是( )
A. B. 1 C. D. 2
(第4题) (第5题) (第6题)
5.(2023·浙江杭州江干区期中)如图,在△ABC中,∠C=90°,∠A=30°,D是AC的中点,若过点D沿直线剪下一个与△ABC相似的小三角形,则不同的剪法共有 ( )
A. 3种 B. 2种 C. 1种 D. 4种
6.(2023·安徽宣城宣化区期末)如图,F为 ABCD的边AD上一点,射线BF交CD的延长线于点E,则下列结论正确的是 ( )
A. = B. = C. = D. =
7.在平面直角坐标系中,矩形OABC的顶点O为原点,边OA在x轴的正半轴上,边OC在y轴的正半轴上,点B的坐标是(6,4).如果矩形OA'B'C'与矩形OABC关于点O位似,且矩形OA'B'C'的面积等于矩形OABC的面积的,那么点B'的坐标是 ( )
A. (3,2) B. (-2,-3) C. (3,2)或(-3,-2) D. (2,3)或(-2,-3)
8.如图,在正方形ABCD中,E为AB的中点,G,F分别为AD,BC边上的点.若AG=1,BF=2,∠GEF=90°,则GF的长为 ( )
A. 2 B. 3 C. 4 D. 5
(第8题) (第9题)
9.如图,在菱形ABCD中,∠A=60°,点E为边AD上一点,连接BE,CE,其中CE交对角线BD于点F.若AB=2,AE=DF,则AE等于 ( )
A. 3± B. 3- C. D.
10.(2022·浙江诸暨模拟)如图,将一张面积为50的大三角形纸片沿着虚线剪成三张小三角形纸片与一张矩形纸片.根据图中标出的长度,则矩形纸片的面积为 ( )
A. 12 B. 18 C. 24 D. 30
二、填空题(本大题共4小题,每小题5分,满分20分)
11.[中考创新题型|开放性试题](2023·北京通州区期中)如图,在△ABC中,AB=AC,点D在AC上(不与点A,C重合),只需添加一个条件即可证明△ABC和△BDC相似,这个条件可以是 (写出一个即可).
(第11题) (第13题) (第14题)
12.(2022·四川成都锦江区段考)已知△ABC与△DEF的相似比为3∶5.若它们周长差是24,则△DEF的周长为 .
13.[课标理念|关注数学文化](2022·北京东城区二模)据《墨经》记载,在两千多年前,我国墨子和他的学生做了世界上第一个“小孔成像”的实验,阐释了光的直线传播原理,如图(1)所示.在如图(2)所示的小孔成像实验中,若物距为10 cm,像距为15 cm,蜡烛火焰倒立的像的高度是6 cm,则蜡烛火焰的高度是 cm.
14.(2022·安徽合肥五十中月考)如图,在正方形ABCD中,AB=4,M为BC的中点,点N在射线AD上,过点N作NE⊥AM于点E,连接MN,则:
(1)= ;
(2)当△MEN与△ABM相似时,AN= .
三、(本大题共2小题,每小题8分,满分16分)
15.(2022·安徽合肥期中)如图,BE是△ABC的角平分线,延长BE至点D,使得BC=CD. 求证:△AEB∽△CED.
16.(2023·浙江绍兴柯桥区期中)已知线段a,b,c满足==,且a+2b+c=26.
(1)求线段a,b,c的长;
(2)若线段m是线段a,b的比例中项,求线段m的长.
四、(本大题共2小题,每小题8分,满分16分)
17. (2023·浙江杭州西湖区期中)如图,在Rt△ABC中,∠C=90°,D是AB的中点,DE∥BC,BE⊥AB.
(1)求证:△DEB∽△BAC;
(2)若AB=6,AC=2,求的值.
18.(2023·广州深圳福田区期中)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1.
(2)以原点O为位似中心,相似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2.
(3)点C2的坐标为 ;△ABC与△A2B2C2的周长比是 .
五、(本大题共2小题,每小题10分,满分20分)
19.[课标理念|关注数学文化]《九章算术》的“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木 ”大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好可以看到位于A处的树木(即点D在直线AC上).
20.如图,在△ABC中,AB=AC,点D,E,F分别在BC,AB,AC上,∠EDF=∠B.
(1)如图(1),求证:DE·CD=DF·BE.
(2)若D为BC的中点,如图(2),连接EF.求证:ED平分∠BEF.
图(1) 图(2)
六、(本题满分12分)
21.[中考创新题型|综合与实践题]某数学兴趣小组为了测量校内路灯的灯柱AB的高度,设计了以下三个方案.
方案一:如图(1),在操场上点C处放一面平面镜,从点C处后退1 m到点D处,恰好在平面镜中看到灯柱的顶部A点的像.再将平面镜向后移动4 m(即FC=4 m)放在F处,从点F处向后退1.5 m到点H处,恰好再次在平面镜中看到灯柱的顶部A点的像,其中眼睛距地面的高度ED,GH均为1.5 m,已知点B,C,D,F,H在同一水平线上,且GH⊥FH,ED⊥CD,AB⊥BH(平面镜的大小忽略不计).
方案二:如图(2),利用标杆CD测量灯柱的高度.已知标杆CD高1.5 m,测得DE=2 m,CE=2.5 m.
方案三:如图(3),将直角三角形支架的直角边CE保持水平,并且边CE与点M在同一直线上.已知两条边CE=0.4 m,EF=0.2 m,测得边CE离地面距离DC=1.5 m.
以上三种方案中,方案 不可行,请选择可行的方案,并求出灯柱的高度.
七、(本题满分12分)
22.[中考新题型|阅读理解题]先阅读下面的材料,然后解答问题.
材料:从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的“完美分割线”.例如:如图(1),AD把△ABC分成△ABD与△ADC,若△ABD是等腰三角形,且△ADC∽△BAC,那么AD就是△ABC的“完美分割线”.
解答下列问题:
(1)如图(2),在△ABC中,∠B=40°,AD是△ABC的“完美分割线”,且△ABD是以AD为底边的等腰三角形,则∠CAD= °;
(2)在△ABC中,∠B=42°,AD是△ABC的“完美分割线”,且△ABD是等腰三角形,求∠BAC的度数.
图(1) 图(2)
八、(本题满分14分)
23.(2023·安徽安庆迎江区期中)在△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE,线段AC与DE交于点G,连接BD,CE.
(1)如图(1),当B,D,E三点共线时,求证:∠BEC=∠DAE.
(2)如图(2),当B,D,E三点不共线时,延长ED交BC于点F.
①求证:AD·CG=EG·FC;
②若∠BAC=∠ADB=90°,求 的值.
图(1) 图(2)
第22章 相似形
1 2 3 4 5 6 7 8 9 10
B C B C A B C B B C
11.∠A=∠CBD(答案不唯一,或∠ABC=∠BDC等) 12.60
13.4 14.(1) (2)2或5
1.B ∵四条线段a,b,c,d是成比例线段,∴a∶b=c∶d,即a∶3=4∶6,∴a=2 cm.
2.C 两个正方形,形状相同,大小不一定相同,符合相似形定义,故选C.
3.B ∵△ABC∽△DEF,∴∠D=∠A=30°,∴∠F=180°-∠D-∠E=100°.
4.C 如图,过点A作平行横线的垂线,交点B所在的平行横线于点D,交点C所在的平行横线于点E.由题意可得,=,即=2,解得BC=.
5.A 如图,在AB边上取一点F,连接DF,使DF∥BC,此时易得△ADF∽△ACB;在BC边上取一点G,连接DG,使DG∥AB,此时易得△CDG∽△CAB;在AB边上取一点E,连接DE,使DE⊥AB,此时易得△ADE∽△ABC.故不同的剪法共有3种.
6.B ∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,∴△ABF∽△DEF,△EFD∽△EBC,∴=,=,=,故选项A,C,D错误;∵△ABF∽△DEF,△EFD∽△EBC,∴△ABF∽△CEB,∴=.故选B.
7.C 由题意知,矩形OA'B'C'与矩形OABC的相似比是1∶2.如图,∵点B的坐标是(6,4),∴点B'的坐标是(3,2)或(-3,-2).
8.B ∵四边形ABCD是正方形,∴∠A=∠B=90°,∴∠AGE+∠AEG=90°.∵∠AEG+∠BEF=90°,∴∠AGE=∠BEF,∴△AGE∽△BEF,∴= .
∵E为AB的中点,∴AE=BE.∵AG=1,BF=2,∴=,解得AE=.在Rt△AEG中,GE2=AG2+AE2=3.在Rt△BEF中,EF2=BE2+BF2=6.在Rt△GEF中,GF==3.
9.B ∵四边形ABCD是菱形,∠A=60°,∴△ABD和△CBD都是等边三角形,∴AD=BD=AB=2.∵AD∥BC,∴∠EDF=∠CBF,∠DEF=∠BCF,
∴△DEF∽△BCF,∴=.又AE=DF,∴=,解得AE=3±.由题意可得0
DE∥BC,∴∠ADE=∠ABC,∠AED=∠ACB,∴△ADE∽△ABC,∴=,即=,∴MH=4,∴DF=4,∴S矩形DFGE=DE·DF=6×4=24.
11.∠A=∠CBD(答案不唯一,或∠ABC=∠BDC等) ∵∠A=∠CBD,∠ACB=∠BCD,∴△ABC∽△BDC.
12.60 ∵△ABC与△DEF的相似比为3∶5,∴△ABC与△DEF的周长比是3∶5.由题意设△ABC的周长为3x,则△DEF的周长为5x,则有5x-3x=24,解得x=12,∴5x=60,∴△DEF的周长为60.
13.4 设蜡烛火焰的高度是x cm,由相似三角形的性质得=,解得x=4,即蜡烛火焰的高度是4 cm.
14.(1) (2)2或5 (1)∵四边形ABCD是正方形,∴AB=BC=AD=4.∵点M是BC的中点,∴BM=CM=2,∴AM===2.
∵BC∥AD,NE⊥AM,∴△ABM∽△NEA,∴==.(2)当∠AMB=∠NME时,则△ABM∽△NEM,∴∠AMB=∠NME=∠MAN,∴AN=MN.∵EN⊥AM,
∴AE=EM=.∵=,∴AN=5.如图,当∠BAM=∠EMN时,△ABM∽△MEN,∴∠MAN+∠AMN=90°,∴∠ANM=90°,∴四边形ABMN是矩形,∴AN=BM=2.综上所述,AN的长为2或5.
15.【参考答案】证明:∵BE是△ABC的角平分线,
∴∠ABE=∠CBE. (2分)
∵BC=CD,
∴∠CBE=∠D, (4分)
∴∠ABE=∠D. (6分)
∵∠AEB=∠CED,
∴△AEB∽△CED. (8分)
16.【参考答案】(1)(设参法)设===k,
则a=3k,b=2k,c=6k.
∵a+2b+c=26,
∴3k+2×2k+6k=26,
解得k=2,
∴a=6,b=4,c=12. (4分)
(2)∵线段m是线段a,b的比例中项,
∴=,即m2=ab=4×6=24,
解得m=2或m=-2(舍去),
∴线段m的长为2. (8分)
17.【解题思路】(1)由DE∥BC得,∠EDB=∠ABC.根据垂直说明∠EBD=∠C=90°,即可得出结论.(2)先由勾股定理求出BC的长,再由相似三角形的面积比等于相似比的平方,即可求得结论.
【参考答案】(1)证明:∵∠C=90°,BE⊥AB,
∴∠EBD=∠C=90°. (2分)
∵DE∥BC,
∴∠EDB=∠ABC,
∴△DEB∽△BAC. (5分)
(2)由勾股定理得BC===4.(6分)
∵D是AB的中点,AB=6,
∴DB=3.
∵△DEB∽△BAC,
∴=()2=()2=. (8分)
18.【参考答案】(1)如图,△A1B1C1为所作. (3分)
(2)如图,△A2B2C2为所作. (6分)
(3)(-6,4) 1∶2 (8分)
19.【参考答案】由题意知DH=DK=100步,AH=15步.
∵AH∥DK,∴∠CDK=∠A.
又∠CKD=∠DHA,∴△CDK∽△DAH, (5分)
∴=,即=,
∴CK=步. (9分)
答:出南门步恰好看到位于A处的树木. (10分)
20.【参考答案】(1)证明:∵AB=AC,∴∠B=∠C.
∵∠B+∠BDE+∠DEB=180°,
∠BDE+∠EDF+∠FDC=180°,
∠EDF=∠B,
∴∠FDC=∠DEB,∴△BDE∽△CFD,
∴=,
即DE·CD=DF·BE. (5分)
(2)证明:由(1)可知=.
∵D为BC的中点,∴BD=CD,
∴=,∴=. (8分)
又∠B=∠EDF,
∴△BDE∽△DFE,
∴∠BED=∠DEF,
∴ED平分∠BEF. (10分)
21.【参考答案】二、三 (2分)
解法提示:根据相似三角形的知识可知,
方案二中△ABE缺少边长的条件,
故方案二不可行.
方案三中△AMC缺少边长的条件,
故方案三不可行.
选择方案一. (4分)
∵∠ECD=∠ACB,∠EDC=∠ABC,
∴△ABC∽△EDC,
∴=,
∴AB==1.5BC. (8分)
设BC=x m,
则AB=1.5x m.
同理可得△ABF∽△GHF,
∴=.
∵AB=1.5x m,BF=BC+CF=(x+4)m,GH=1.5 m,FH=1.5 m,
∴=,
解得x=8,
∴AB=1.5×8=12(m),
即灯柱的高度为12 m. (12分)
22.【参考答案】(1)40 (4分)
解法提示:∵AD是△ABC的“完美分割线”,
∴△DAC∽△ABC,∴∠CAD=∠B=40°.
(2)若BD=AD,∵AD是△ABC的“完美分割线”,
∴△DAC∽△ABC,
∴∠CAD=∠B=42°.
∵AD=BD,
∴∠ABD=∠BAD=42°,
∴∠BAC=∠BAD+∠CAD=84°. (6分)
若AB=BD,则∠BAD=69°=∠BDA.
∵AD是△ABC的“完美分割线”,
∴△DAC∽△ABC,
∴∠CAD=∠B=42°,
∴∠BAC=∠BAD+∠CAD=69°+42°=111°. (9分)
若AB=AD,则∠B=∠ADB=42°.
∵AD是△ABC的“完美分割线”,
∴△DAC∽△ABC,
∴∠CAD=∠B=42°.
∵∠ADB=∠DAC+∠C=42°+∠C≠42°,
∴不符合题意. (11分)
综上所述,∠BAC的度数为84°或111°. (12分)
23.【参考答案】(1)证明:∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠CAE.
又∵AB=AC,AD=AE,
∴△BAD≌△CAE,
∴∠ADB=∠AEC.
当B,D,E三点共线时,∠ADB=∠AED+∠DAE.
又∵∠AEC=∠AED+∠BEC,
∴∠BEC=∠DAE. (5分)
(2)①证明:∵AB=AC,AD=AE,
∴=.
又∠BAC=∠DAE,
∴△BAC∽△DAE,
∴∠AED=∠ACB.
又∠AGE=∠FGC,
∴△AEG∽△FCG,
∴=,即AE·CG=EG·FC.
又AD=AE,
∴AD·CG=EG·FC. (10分)
②如图,连接AF.
由(1)可知,△BAD≌△CAE,
∴∠AEC=∠ADB=90°.
由①知△AEG∽△FCG,
∴=,即=.
又∠AGF=∠EGC,
∴△AGF∽△EGC,
∴∠AFG=∠ACE,
∴∠AFE+∠EFC=∠ECA+∠EAC=180°-∠AEC=90°,
∴∠AFC=90°,
∴FC=AC=AB,
∴=. (14分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
