第23章 图形的相似单元测试题(含答案)
文档属性
| 名称 | 第23章 图形的相似单元测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 572.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-10 17:27:01 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025华师版九年级数学上册
第23章 图形的相似
时间:90分钟 满分:100分
一、选择题(每小题3分,共30分)
1.用放大镜观察一个五边形时,不变的量是( )
A.各边的长度 B.五边形的周长 C.各内角的度数 D.五边形的面积
2.在平面直角坐标系中,点(2,3)关于原点对称的点的坐标是( )
A.(-2,3) B.(2,-3) C.(3,2) D.(-2,-3)
3.下列各组图形中一定是相似图形的是( )
A.两个平行四边形 B.两个菱形 C.两个等腰梯形 D.两个等边三角形
4.如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段AB=3,则线段BC的长是( )
A. B.1 C. D.2
5.一张矩形纸片对折后与原矩形相似,则原矩形与对折后矩形的相似比是( )
A.∶1 B.4∶1 C.3∶1 D.2∶1
6.如图,F为 ABCD的边AD上一点,射线BF交CD的延长线于点E,则下列结论正确的是( )
A.= B.= C.= D.=
7.在平面直角坐标系中,点A(-6,2),B(-4,-6),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A'的坐标是( )
A.(-3,1) B.(-2,-3)
C.(-3,1)或(3,-1) D.(-2,-3)或(2,3)
8.如图,在四边形ABCD中,R,P分别是BC,CD边上的点,E,F分别是AP,RP的中点,当点P在CD上从点C向点D移动而点R不动时,则下列结论成立的是( )
A.线段EF的长逐渐增大 B.线段EF的长逐渐减小
C.线段EF的长不变 D.线段EF的长与点P的位置有关
9.如图,以点O为位似中心,将△ABC放大得到△DEF.若AD=OA,△ABC与△DEF的周长之比为a∶b,则=( )
A.1∶5 B.1∶4 C.1∶3 D.1∶2
10.如图,在钝角三角形ABC中,AB=6 cm,AC=12 cm,动点D从点A出发沿AB以1 cm/s的速度向点B运动,同时动点E从点C出发沿CA以2 cm/s的速度向点A运动,当以A,D,E为顶点的三角形与△ABC相似时,运动时间是( )
A.3 s或4.8 s B.3 s C.4.5 s D.4.5 s或4.8 s
二、填空题(每小题3分,共18分)
11.若=,则= .
12.生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a与全身b的高度比值接近0.618,可增加视觉美感.若图中b为2m,则a约为
m.(保留两位小数)
13.如图,E,F分别为矩形ABCD的边AD,CD上的点,∠BEF=90°,则图中①、②、③、④四个三角形中,一定相似的是 和 . (填序号)
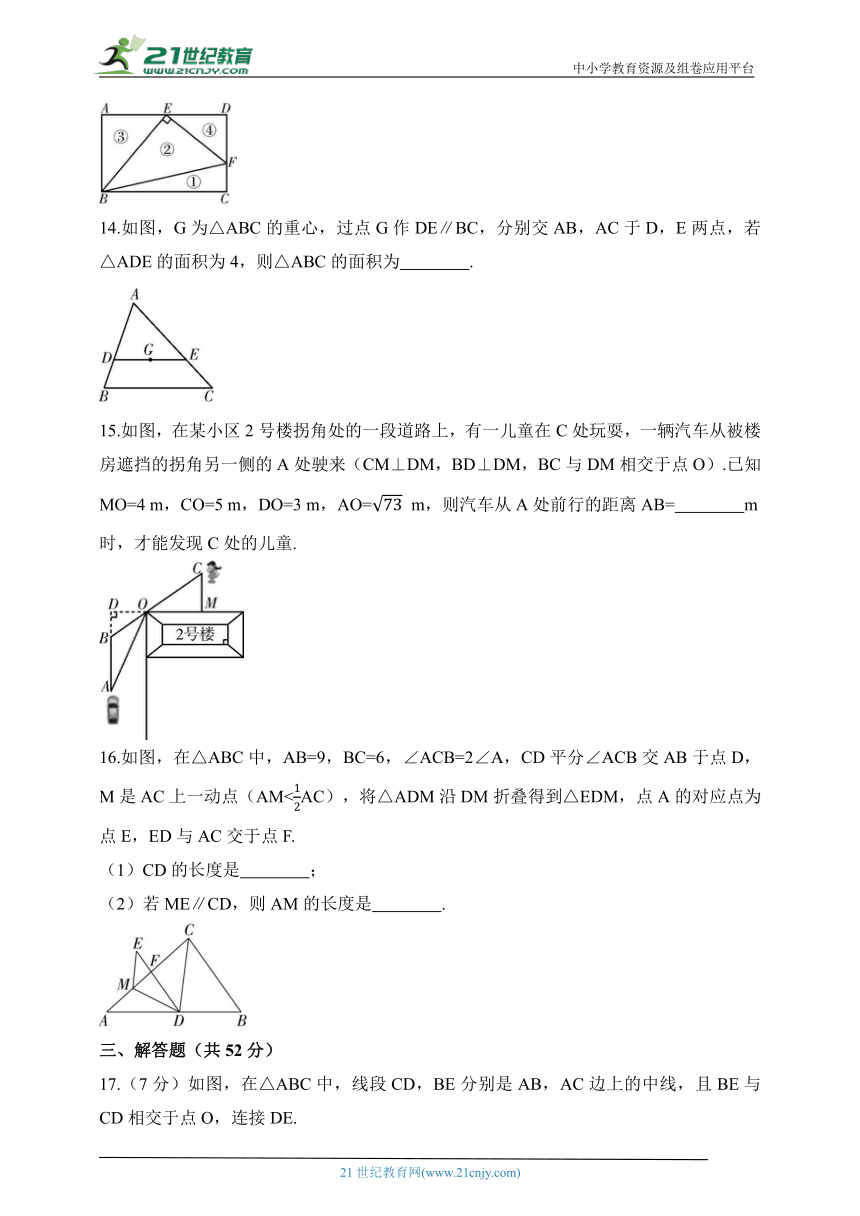
14.如图,G为△ABC的重心,过点G作DE∥BC,分别交AB,AC于D,E两点,若△ADE的面积为4,则△ABC的面积为 .
15.如图,在某小区2号楼拐角处的一段道路上,有一儿童在C处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的A处驶来(CM⊥DM,BD⊥DM,BC与DM相交于点O).已知MO=4 m,CO=5 m,DO=3 m,AO= m,则汽车从A处前行的距离AB= m时,才能发现C处的儿童.
16.如图,在△ABC中,AB=9,BC=6,∠ACB=2∠A,CD平分∠ACB交AB于点D,M是AC上一动点(AM(1)CD的长度是 ;
(2)若ME∥CD,则AM的长度是 .
三、解答题(共52分)
17.(7分)如图,在△ABC中,线段CD,BE分别是AB,AC边上的中线,且BE与CD相交于点O,连接DE.
(1)若DE=3,则BC= ;
(2)判断线段OB和OE之间的数量关系,并证明你的结论.
18.(8分)在如图所示的平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,-2),B(2,-1),C(4,-3).
(1)画出△A1B1C1,使它与△ABC关于x轴对称;
(2)以点(4,0)为位似中心,在图中画出△A1B1C1的位似图形△A2B2C2,且△A2B2C2与△A1B1C1的相似比为2∶1,并直接写出点A2的坐标.
19.(8分)如图,在△ABC中,AB=AC,∠A=36°.
(1)求作:∠ABC的平分线BD交AC于点D.(要求:尺规作图,保留作图痕迹,不写作法)
(2)求证:点D为线段AC的黄金分割点(即AD2=CD·CA).
20.(9分)某校社会实践小组为了测量大雁塔的高度,如图,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,大雁塔的塔尖点B正好在同一直线上,测得EC=4米,将标杆向后平移到点G处,这时地面上的点F,标杆的顶端点H,大雁塔的塔尖点B正好在同一直线上(点F,G,E,C,A在同一直线上),这时测得FG=6米,CG=60米.
(1)请你根据以上数据,计算大雁塔的高度AB.
(2)“景点简介”显示,大雁塔的高度约为64.5米.请计算本次测量的误差,并提出一条减小误差的合理化建议.
21.(10分)如图,在 ABCD中,AC,BD交于点O,点M是AD的中点,连接MC交BD于点N,ON=1.
(1)求证:△DMN∽△BCN.
(2)求BD的长.
(3)若△DCN的面积为2,直接写出四边形ABNM的面积.
22.(10分)(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.
填空:①的值为 ; ②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,==,连接AC,交BD的延长线于点M.请求出的值及∠AMB的度数,并说明理由.
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M.若OD=1,OB=,请直接写出当点C与点M重合时AC的长.
参考答案与解析
1.C
2.D
3.D
4.C 如图,过点A作平行横线的垂线,交点B所在的平行横线于点D,交点C所在的平行横线于点E,由题意可得,=,即=2,解得BC=.
5.A 解法一 如图,设原矩形的长为2a,宽为b,则对折后的矩形的长为b,宽为a.∵对折后所得的矩形与原矩形相似,∴=,∴2a2=b2,∴=,∴原矩形与对折后矩形的相似比是∶1.
解法二 ∵矩形纸片对折后和原矩形相似,∴原矩形面积是对折后矩形面积的2倍,∴原矩形与对折后矩形的相似比是∶1.
6.B ∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,∴△ABF∽△DEF
,△EFD∽△EBC,∴=,=,=,故选项A,C,D错误;∵△ABF∽△DEF,△EFD∽△EBC,∴△ABF∽△CEB,∴=.
7.C ∵点A(-6,2),B(-4,-6),以原点O为位似中心,相似比为,把△ABO缩小,∴点A的对应点A'的坐标为(-6×,2×)或[-6×(-),2×(-)
],即A'(-3,1)或(3,-1).
8.C 连接AR,则EF是△PAR的中位线,∴EF=AR,∴线段EF的长不变.
9.D ∵以点O为位似中心,将△ABC放大得到△DEF,AD=OA,∴==,∴△ABC与△DEF的周长之比为a∶b=1∶2,则b=2a,故原式==.
10.A 设运动t s时,以点A,D,E为顶点的三角形与△ABC相似,则AD=
t cm,CE=2t cm,AE=AC-CE=(12-2t)(cm),①当D与B对应时,有△ADE
∽△ABC,∴AD∶AB=AE∶AC,∴t∶6=(12-2t)∶12,∴t=3;②当D与C对应时,有△ADE∽△ACB,∴AD∶AC=AE∶AB,∴t∶12=(12-2t)∶6,∴
t=4.8,∴当以点A,D,E为顶点的三角形与△ABC相似时,运动的时间是3 s或4.8 s.
11. ∵=,∴=,∴=1-=1-=.
12.1.24 ∵雕像的腰部以下a与全身b的高度比值接近0.618,∴≈0.618.∵b=
2m,∴≈0.618,即a≈1.24m.
13.③④(或④③) ∵四边形ABCD是矩形,∴∠A=∠D=90°,∴∠ABE
+∠AEB=90°,∵∠BEF=90°,∴∠AEB+∠DEF=90°,∴∠ABE=∠DEF,∴
△ABE∽△DEF,即③和④一定相似.
14.9 如图,连接AG并延长AG交BC于H,∵G为△ABC的重心,∴AG
=2GH,∵DE∥BC,∴==,∵DE∥BC,∴△ADE∽△ABC,相似比为,∴△ADE与△ABC的面积比为,∵△ADE的面积为4,∴△ABC的面积为9.
15.5.75 在Rt△CMO中,MO=4 m,CO=5 m,∴CM===3(m),∵∠BOD=∠MOC,∠BDO=∠CMO=90°,∴△BDO∽△CMO,∴=,∴=,∴BD=2.25 m,在Rt△AOD中,AO= m,DO=3 m,∴AD==
=8(m),∴AB=AD - BD=8-2.25=5.75(m),∴汽车从A处前行5.75 m,才能发现C处的儿童.
16.(1)5;(2)2.5 (1)∵CD平分∠ACB,∴∠ACB=2∠ACD=2∠BCD.
∵∠ACB=2∠A,∴∠ACD=∠A=∠BCD,∴AD=CD.∵∠A=∠BCD,∠B=
∠B,∴△ABC∽△CBD,∴=,∴=,∴BD=4,∴AD=AB -BD=9-4=5,∴CD=AD=5,∴CD的长度是5.(2)由翻折可知DE=AD=5,∠E=∠A,∴
∠E=∠ACD.∵ME∥CD,∴∠E=∠EDC,∠EMC=∠ACD,∴∠ACD=∠EDC,∠EMC=∠E,∴FC=FD,FE=FM,∴FC+FM=FD+EF,∴CM=DE=AD=5.∵
△ABC∽△CBD,∴=,∴=,∴AC=7.5,∴AM=AC-CM=7.5-5=2.5,∴AM的长度是2.5.
17.解:(1)6(3分)
∵线段CD,BE分别是AB,AC边上的中线,∴DE是△ABC的中位线,∴BC
=2DE=2×3=6.
(2)OB=2OE.证明如下:
∵线段CD,BE分别是AB,AC边上的中线,∴DE是△ABC的中位线,
∴DE∥BC,BC=2DE,∴△DOE∽△COB,(5分)
∴=,∴OB=2OE.(7分)
18.解:(1)如图,△A1B1C1即为所求.(3分)
(2)如图,△A2B2C2即为所求.(6分)
点A2的坐标为(-2,4).(8分)
19.(1)解:∠ABC的平分线BD交AC于点D,如图.
(3分)
(2)证明:在△ABC中,AB=AC,∠A=36°,∴∠ABC=∠ACB=72°.
∵BD平分∠ABC,∴∠ABD=∠CBD=36°,
∴AD=BD,∠BDC=72°,∴BD=BC,∴AD=BC.(6分)
∵∠BCD=∠ACB,∠CBD=∠CAB,∴△BCD∽△ACB,
∴BC∶AC=CD∶BC,∴AD∶AC=CD∶AD,∴AD2=CD·CA,
∴点D为线段AC的黄金分割点.(8分)
20.解:(1)∵DC∥AB,∴△EDC∽△EBA,∴=.
∵GH∥AB,∴△FHG∽△FBA,∴=.(4分)
∵DC=HG,∴=,∴=,解得CA=120.
∵=,∴=,解得AB=62.
答:大雁塔的高度AB为62米.(7分)
(2)误差为64.5-62=2.5(米).
减小误差的建议:可多次测量,取测量数据的平均值(答案合理即可).(9分)
21.(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,
∴∠DMN=∠BCN,∠MDN=∠CBN,∴△DMN∽△BCN.(3分)
(2)解:∵四边形ABCD是平行四边形,∴AD=BC,OB=OD=BD.
∵△DMN∽△BCN,∴=.
∵M为AD的中点,∴AD=2DM,∴BC=2DM,∴BN=2DN,
设OB=OD=x,∴BD=2x,∴BN=OB+ON=x+1,DN=OD -ON=x-1,
∴x+1=2(x-1),解得x=3,∴BD=2x=6,∴BD的长为6.(6分)
(3)解:∵△DMN∽△BCN,∴DM∶BC=MN∶CN=DN∶BN=1∶2.
∵△DCN的面积为2,∴S△MND=S△DCN=1,S△BNC=2S△DCN=4,
∴S△ABD=S△BCD=S△BNC+S△DCN=4+2=6,∴S四边形ABNM=S△ABD -S△MND=6-1=5,
∴四边形ABNM的面积为5.(10分)
22.解:(1)①1(1分)
①∵∠AOB=∠COD,∴∠BOD=∠AOC.又∵OC=OD,OA=OB,∴△AOC
≌△BOD,∴AC=BD,∠OBD=∠OAC,∴=1.
② 40°(2分)
②设BD,OA交于点N,∵∠MNA=∠ONB,∠OBD=∠OAC,∴∠AMB=
∠AOB=40°.
(2)=,∠AMB=90°.理由如下:(4分)
∵∠AOB=∠COD=90°,
∴∠COD+∠AOD=∠AOB+∠AOD,即∠AOC=∠BOD.
∵==,∴△AOC∽△BOD,∴==,∠CAO=∠DBO.(6分)
设AO,BM交于点P,
∵∠APM=∠BPO,∴∠AMB=∠AOB=90°.(8分)
(3)AC的长为2或3.(10分)
由(2)可知,∠AMB=90°,=,设BD=x,则AC=x.∵OB=,∠AOB
=90°,=,∴易得AB=2,同理,易得MD=2.分两种情况讨论.如图1,当点M,C在OA上侧重合时,在Rt△ABC中,AB2=AC2+BC2,∴(2)2=
(x)2+(x+2)2,解得x1=2,x2=-3(不合题意,舍去), ∴AC=x=2.
如图2,当点M,C在OA下侧重合时,
在Rt△ABC中,AB2=AC2+BC2,∴(2)2=(x)2+(x-2)2,
解得x1=-2(不合题意,舍去),x2=3, ∴AC=x=3.
综上,AC的长为2或3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025华师版九年级数学上册
第23章 图形的相似
时间:90分钟 满分:100分
一、选择题(每小题3分,共30分)
1.用放大镜观察一个五边形时,不变的量是( )
A.各边的长度 B.五边形的周长 C.各内角的度数 D.五边形的面积
2.在平面直角坐标系中,点(2,3)关于原点对称的点的坐标是( )
A.(-2,3) B.(2,-3) C.(3,2) D.(-2,-3)
3.下列各组图形中一定是相似图形的是( )
A.两个平行四边形 B.两个菱形 C.两个等腰梯形 D.两个等边三角形
4.如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段AB=3,则线段BC的长是( )
A. B.1 C. D.2
5.一张矩形纸片对折后与原矩形相似,则原矩形与对折后矩形的相似比是( )
A.∶1 B.4∶1 C.3∶1 D.2∶1
6.如图,F为 ABCD的边AD上一点,射线BF交CD的延长线于点E,则下列结论正确的是( )
A.= B.= C.= D.=
7.在平面直角坐标系中,点A(-6,2),B(-4,-6),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A'的坐标是( )
A.(-3,1) B.(-2,-3)
C.(-3,1)或(3,-1) D.(-2,-3)或(2,3)
8.如图,在四边形ABCD中,R,P分别是BC,CD边上的点,E,F分别是AP,RP的中点,当点P在CD上从点C向点D移动而点R不动时,则下列结论成立的是( )
A.线段EF的长逐渐增大 B.线段EF的长逐渐减小
C.线段EF的长不变 D.线段EF的长与点P的位置有关
9.如图,以点O为位似中心,将△ABC放大得到△DEF.若AD=OA,△ABC与△DEF的周长之比为a∶b,则=( )
A.1∶5 B.1∶4 C.1∶3 D.1∶2
10.如图,在钝角三角形ABC中,AB=6 cm,AC=12 cm,动点D从点A出发沿AB以1 cm/s的速度向点B运动,同时动点E从点C出发沿CA以2 cm/s的速度向点A运动,当以A,D,E为顶点的三角形与△ABC相似时,运动时间是( )
A.3 s或4.8 s B.3 s C.4.5 s D.4.5 s或4.8 s
二、填空题(每小题3分,共18分)
11.若=,则= .
12.生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a与全身b的高度比值接近0.618,可增加视觉美感.若图中b为2m,则a约为
m.(保留两位小数)
13.如图,E,F分别为矩形ABCD的边AD,CD上的点,∠BEF=90°,则图中①、②、③、④四个三角形中,一定相似的是 和 . (填序号)
14.如图,G为△ABC的重心,过点G作DE∥BC,分别交AB,AC于D,E两点,若△ADE的面积为4,则△ABC的面积为 .
15.如图,在某小区2号楼拐角处的一段道路上,有一儿童在C处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的A处驶来(CM⊥DM,BD⊥DM,BC与DM相交于点O).已知MO=4 m,CO=5 m,DO=3 m,AO= m,则汽车从A处前行的距离AB= m时,才能发现C处的儿童.
16.如图,在△ABC中,AB=9,BC=6,∠ACB=2∠A,CD平分∠ACB交AB于点D,M是AC上一动点(AM
(2)若ME∥CD,则AM的长度是 .
三、解答题(共52分)
17.(7分)如图,在△ABC中,线段CD,BE分别是AB,AC边上的中线,且BE与CD相交于点O,连接DE.
(1)若DE=3,则BC= ;
(2)判断线段OB和OE之间的数量关系,并证明你的结论.
18.(8分)在如图所示的平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,-2),B(2,-1),C(4,-3).
(1)画出△A1B1C1,使它与△ABC关于x轴对称;
(2)以点(4,0)为位似中心,在图中画出△A1B1C1的位似图形△A2B2C2,且△A2B2C2与△A1B1C1的相似比为2∶1,并直接写出点A2的坐标.
19.(8分)如图,在△ABC中,AB=AC,∠A=36°.
(1)求作:∠ABC的平分线BD交AC于点D.(要求:尺规作图,保留作图痕迹,不写作法)
(2)求证:点D为线段AC的黄金分割点(即AD2=CD·CA).
20.(9分)某校社会实践小组为了测量大雁塔的高度,如图,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,大雁塔的塔尖点B正好在同一直线上,测得EC=4米,将标杆向后平移到点G处,这时地面上的点F,标杆的顶端点H,大雁塔的塔尖点B正好在同一直线上(点F,G,E,C,A在同一直线上),这时测得FG=6米,CG=60米.
(1)请你根据以上数据,计算大雁塔的高度AB.
(2)“景点简介”显示,大雁塔的高度约为64.5米.请计算本次测量的误差,并提出一条减小误差的合理化建议.
21.(10分)如图,在 ABCD中,AC,BD交于点O,点M是AD的中点,连接MC交BD于点N,ON=1.
(1)求证:△DMN∽△BCN.
(2)求BD的长.
(3)若△DCN的面积为2,直接写出四边形ABNM的面积.
22.(10分)(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.
填空:①的值为 ; ②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,==,连接AC,交BD的延长线于点M.请求出的值及∠AMB的度数,并说明理由.
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M.若OD=1,OB=,请直接写出当点C与点M重合时AC的长.
参考答案与解析
1.C
2.D
3.D
4.C 如图,过点A作平行横线的垂线,交点B所在的平行横线于点D,交点C所在的平行横线于点E,由题意可得,=,即=2,解得BC=.
5.A 解法一 如图,设原矩形的长为2a,宽为b,则对折后的矩形的长为b,宽为a.∵对折后所得的矩形与原矩形相似,∴=,∴2a2=b2,∴=,∴原矩形与对折后矩形的相似比是∶1.
解法二 ∵矩形纸片对折后和原矩形相似,∴原矩形面积是对折后矩形面积的2倍,∴原矩形与对折后矩形的相似比是∶1.
6.B ∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,∴△ABF∽△DEF
,△EFD∽△EBC,∴=,=,=,故选项A,C,D错误;∵△ABF∽△DEF,△EFD∽△EBC,∴△ABF∽△CEB,∴=.
7.C ∵点A(-6,2),B(-4,-6),以原点O为位似中心,相似比为,把△ABO缩小,∴点A的对应点A'的坐标为(-6×,2×)或[-6×(-),2×(-)
],即A'(-3,1)或(3,-1).
8.C 连接AR,则EF是△PAR的中位线,∴EF=AR,∴线段EF的长不变.
9.D ∵以点O为位似中心,将△ABC放大得到△DEF,AD=OA,∴==,∴△ABC与△DEF的周长之比为a∶b=1∶2,则b=2a,故原式==.
10.A 设运动t s时,以点A,D,E为顶点的三角形与△ABC相似,则AD=
t cm,CE=2t cm,AE=AC-CE=(12-2t)(cm),①当D与B对应时,有△ADE
∽△ABC,∴AD∶AB=AE∶AC,∴t∶6=(12-2t)∶12,∴t=3;②当D与C对应时,有△ADE∽△ACB,∴AD∶AC=AE∶AB,∴t∶12=(12-2t)∶6,∴
t=4.8,∴当以点A,D,E为顶点的三角形与△ABC相似时,运动的时间是3 s或4.8 s.
11. ∵=,∴=,∴=1-=1-=.
12.1.24 ∵雕像的腰部以下a与全身b的高度比值接近0.618,∴≈0.618.∵b=
2m,∴≈0.618,即a≈1.24m.
13.③④(或④③) ∵四边形ABCD是矩形,∴∠A=∠D=90°,∴∠ABE
+∠AEB=90°,∵∠BEF=90°,∴∠AEB+∠DEF=90°,∴∠ABE=∠DEF,∴
△ABE∽△DEF,即③和④一定相似.
14.9 如图,连接AG并延长AG交BC于H,∵G为△ABC的重心,∴AG
=2GH,∵DE∥BC,∴==,∵DE∥BC,∴△ADE∽△ABC,相似比为,∴△ADE与△ABC的面积比为,∵△ADE的面积为4,∴△ABC的面积为9.
15.5.75 在Rt△CMO中,MO=4 m,CO=5 m,∴CM===3(m),∵∠BOD=∠MOC,∠BDO=∠CMO=90°,∴△BDO∽△CMO,∴=,∴=,∴BD=2.25 m,在Rt△AOD中,AO= m,DO=3 m,∴AD==
=8(m),∴AB=AD - BD=8-2.25=5.75(m),∴汽车从A处前行5.75 m,才能发现C处的儿童.
16.(1)5;(2)2.5 (1)∵CD平分∠ACB,∴∠ACB=2∠ACD=2∠BCD.
∵∠ACB=2∠A,∴∠ACD=∠A=∠BCD,∴AD=CD.∵∠A=∠BCD,∠B=
∠B,∴△ABC∽△CBD,∴=,∴=,∴BD=4,∴AD=AB -BD=9-4=5,∴CD=AD=5,∴CD的长度是5.(2)由翻折可知DE=AD=5,∠E=∠A,∴
∠E=∠ACD.∵ME∥CD,∴∠E=∠EDC,∠EMC=∠ACD,∴∠ACD=∠EDC,∠EMC=∠E,∴FC=FD,FE=FM,∴FC+FM=FD+EF,∴CM=DE=AD=5.∵
△ABC∽△CBD,∴=,∴=,∴AC=7.5,∴AM=AC-CM=7.5-5=2.5,∴AM的长度是2.5.
17.解:(1)6(3分)
∵线段CD,BE分别是AB,AC边上的中线,∴DE是△ABC的中位线,∴BC
=2DE=2×3=6.
(2)OB=2OE.证明如下:
∵线段CD,BE分别是AB,AC边上的中线,∴DE是△ABC的中位线,
∴DE∥BC,BC=2DE,∴△DOE∽△COB,(5分)
∴=,∴OB=2OE.(7分)
18.解:(1)如图,△A1B1C1即为所求.(3分)
(2)如图,△A2B2C2即为所求.(6分)
点A2的坐标为(-2,4).(8分)
19.(1)解:∠ABC的平分线BD交AC于点D,如图.
(3分)
(2)证明:在△ABC中,AB=AC,∠A=36°,∴∠ABC=∠ACB=72°.
∵BD平分∠ABC,∴∠ABD=∠CBD=36°,
∴AD=BD,∠BDC=72°,∴BD=BC,∴AD=BC.(6分)
∵∠BCD=∠ACB,∠CBD=∠CAB,∴△BCD∽△ACB,
∴BC∶AC=CD∶BC,∴AD∶AC=CD∶AD,∴AD2=CD·CA,
∴点D为线段AC的黄金分割点.(8分)
20.解:(1)∵DC∥AB,∴△EDC∽△EBA,∴=.
∵GH∥AB,∴△FHG∽△FBA,∴=.(4分)
∵DC=HG,∴=,∴=,解得CA=120.
∵=,∴=,解得AB=62.
答:大雁塔的高度AB为62米.(7分)
(2)误差为64.5-62=2.5(米).
减小误差的建议:可多次测量,取测量数据的平均值(答案合理即可).(9分)
21.(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,
∴∠DMN=∠BCN,∠MDN=∠CBN,∴△DMN∽△BCN.(3分)
(2)解:∵四边形ABCD是平行四边形,∴AD=BC,OB=OD=BD.
∵△DMN∽△BCN,∴=.
∵M为AD的中点,∴AD=2DM,∴BC=2DM,∴BN=2DN,
设OB=OD=x,∴BD=2x,∴BN=OB+ON=x+1,DN=OD -ON=x-1,
∴x+1=2(x-1),解得x=3,∴BD=2x=6,∴BD的长为6.(6分)
(3)解:∵△DMN∽△BCN,∴DM∶BC=MN∶CN=DN∶BN=1∶2.
∵△DCN的面积为2,∴S△MND=S△DCN=1,S△BNC=2S△DCN=4,
∴S△ABD=S△BCD=S△BNC+S△DCN=4+2=6,∴S四边形ABNM=S△ABD -S△MND=6-1=5,
∴四边形ABNM的面积为5.(10分)
22.解:(1)①1(1分)
①∵∠AOB=∠COD,∴∠BOD=∠AOC.又∵OC=OD,OA=OB,∴△AOC
≌△BOD,∴AC=BD,∠OBD=∠OAC,∴=1.
② 40°(2分)
②设BD,OA交于点N,∵∠MNA=∠ONB,∠OBD=∠OAC,∴∠AMB=
∠AOB=40°.
(2)=,∠AMB=90°.理由如下:(4分)
∵∠AOB=∠COD=90°,
∴∠COD+∠AOD=∠AOB+∠AOD,即∠AOC=∠BOD.
∵==,∴△AOC∽△BOD,∴==,∠CAO=∠DBO.(6分)
设AO,BM交于点P,
∵∠APM=∠BPO,∴∠AMB=∠AOB=90°.(8分)
(3)AC的长为2或3.(10分)
由(2)可知,∠AMB=90°,=,设BD=x,则AC=x.∵OB=,∠AOB
=90°,=,∴易得AB=2,同理,易得MD=2.分两种情况讨论.如图1,当点M,C在OA上侧重合时,在Rt△ABC中,AB2=AC2+BC2,∴(2)2=
(x)2+(x+2)2,解得x1=2,x2=-3(不合题意,舍去), ∴AC=x=2.
如图2,当点M,C在OA下侧重合时,
在Rt△ABC中,AB2=AC2+BC2,∴(2)2=(x)2+(x-2)2,
解得x1=-2(不合题意,舍去),x2=3, ∴AC=x=3.
综上,AC的长为2或3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
