第24章 解直角三角形单元测试题(含答案)
文档属性
| 名称 | 第24章 解直角三角形单元测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 573.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-10 17:28:29 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025华师版九年级数学上册
第24章 解直角三角形
时间:90分钟 满分:100分
一、选择题(每小题3分,共30分)
1.tan 45°的值等于( )
A. B. C.1 D.
2.在△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边,下列各式成立的是( )
A.sin B= B.tan B= C.tan B= D.cos B=
3.如图,点A(2,t)在第一象限,OA与x轴所夹锐角为α,tan α=2,则t的值为( )
A.1 B.2 C.4 D.
4.如图,在△ABC中,AB=AC,∠A=120°,D为BC的中点,DE⊥AB于点E,若BC=4,则DE的长为( )
A.1.5 B.2 C.1 D.
5.如图,在4×4的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,则cos∠ABC的值为( )
A. B. C.2 D.
6.在Rt△ABC中,∠C=90°,AC=15,AB边上的中线CD=,则sin A为 ( )
A. B. C. D.
7.如图,已知窗户高AB=m米,窗户外面上方0.2米的点C处安装水平遮阳板CD=n米,当太阳光线与水平线成α角时,光线刚好不能直接射入室内,则m,n的关系式是( )
A.n=m tan α-0.2 B.n=m tan α+0.2
C.m=n tan α-0.2 D.m=n tan α+0.2
8.如图,在Rt△ABC中,∠C=90°,AB=5 cm,tan B=,点D从点A出发沿AC方向以1 cm/s的速度向点C运动.过点D作DE∥AB交BC于点E,过点E作EF⊥BC交AB于点F,当四边形ADEF为菱形时,点D运动的时间为( )
A. s B. s C. s D. s
9.定义:在等腰三角形中,底边与腰的比值叫做顶角的正对,顶角A的正对记作sad A,即sad A=.如图,在△ABC中,AB=AC,∠A=4∠B,则cos B·sad A的值为( )
A.1 B. C. D.
10.我国古代的数学家赵爽在为《周髀算经》作注解时,用4个全等的直角三角形和中间的小正方形拼成一个大正方形,这个图被称为“弦图”,它体现了中国古代数学的成就.如图,已知大正方形ABCD的面积是100,小正方形EFGH的面积是4,那么tan∠ADF=( )
A. B. C.1 D.
二、填空题(每小题3分,共18分)
11.小明站在某商场内的自动扶梯上,当他沿着斜坡向上前进了13米时,他在铅垂方向升高了5米,则该自动扶梯所在的斜坡的坡度i= .
12.如图,在Rt△ABC中,∠ABC=90°,∠C=60°,点D为边AC的中点,BD=
2,则BC的长为 .
13.在△ABC中,∠A,∠B均为锐角,(sin A-1)2+=0,若AB=10,则BC= .
14.对于任意锐角α,β,有等式sin(α+β)=sin α cos β+cos α sin β.结合所学知识,利用上述公式可以求得sin 75°的值是 .(结果保留根号)
15.如图,长尾夹的侧面是△ABC,当AC与AB张开到互相平行时,达到最大夹纸厚度,若AB=AC=15 mm,∠ACB=70°,则该长尾夹最大夹纸厚度约为 mm.(精确到1 mm,参考数据:sin 70°≈0.94,cos 70°≈0.34,tan 70°≈2.75)
16.如图为两个边长为1的正方形组成的2×1格点图,点A,B,C,D都在格点上,AB,CD交于点P,则tan∠BPD= .
三、解答题(共52分)
17.计算:
(1)(3分)3sin 30°·cos 60°-tan230°;
(2)(3分)-cos 30°.
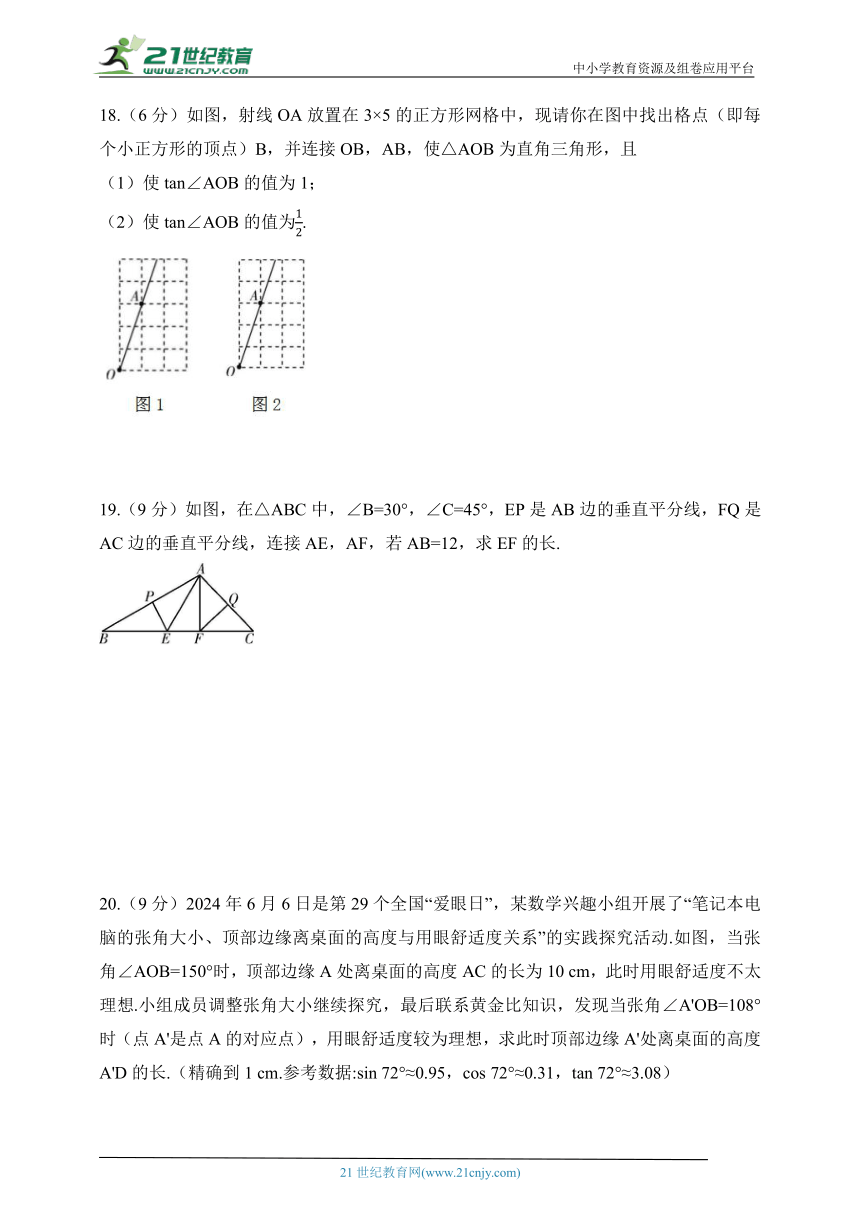
18.(6分)如图,射线OA放置在3×5的正方形网格中,现请你在图中找出格点(即每个小正方形的顶点)B,并连接OB,AB,使△AOB为直角三角形,且
(1)使tan∠AOB的值为1;
(2)使tan∠AOB的值为.
19.(9分)如图,在△ABC中,∠B=30°,∠C=45°,EP是AB边的垂直平分线,FQ是AC边的垂直平分线,连接AE,AF,若AB=12,求EF的长.
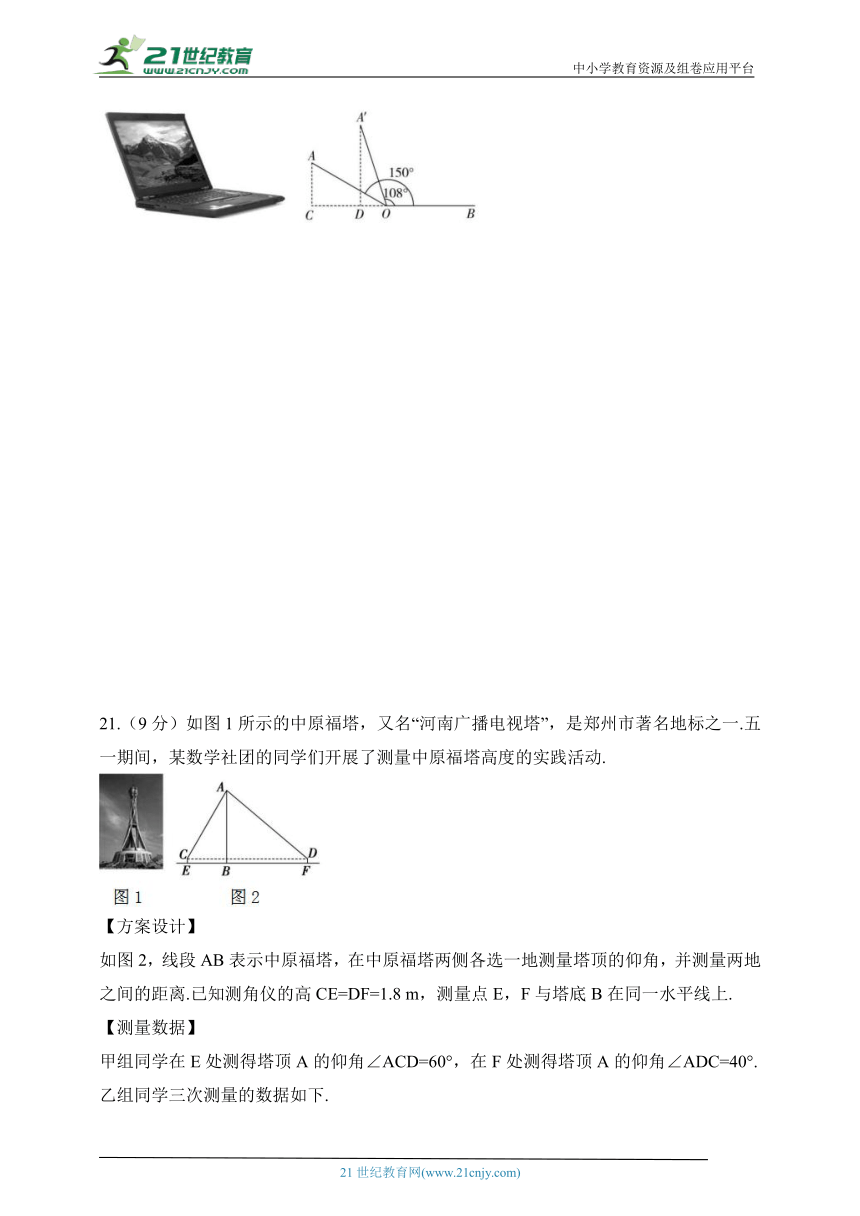
20.(9分)2024年6月6日是第29个全国“爱眼日”,某数学兴趣小组开展了“笔记本电脑的张角大小、顶部边缘离桌面的高度与用眼舒适度关系”的实践探究活动.如图,当张角∠AOB=150°时,顶部边缘A处离桌面的高度AC的长为10 cm,此时用眼舒适度不太理想.小组成员调整张角大小继续探究,最后联系黄金比知识,发现当张角∠A'OB=108°时(点A'是点A的对应点),用眼舒适度较为理想,求此时顶部边缘A'处离桌面的高度A'D的长.(精确到1 cm.参考数据:sin 72°≈0.95,cos 72°≈0.31,tan 72°≈3.08)
21.(9分)如图1所示的中原福塔,又名“河南广播电视塔”,是郑州市著名地标之一.五一期间,某数学社团的同学们开展了测量中原福塔高度的实践活动.
【方案设计】
如图2,线段AB表示中原福塔,在中原福塔两侧各选一地测量塔顶的仰角,并测量两地之间的距离.已知测角仪的高CE=DF=1.8 m,测量点E,F与塔底B在同一水平线上.
【测量数据】
甲组同学在E处测得塔顶A的仰角∠ACD=60°,在F处测得塔顶A的仰角∠ADC=40°.
乙组同学三次测量的数据如下.
【问题解决】
(1)三次测得的E,F之间的距离的平均值是 m.
(2)求中原福塔AB的高度(结果精确到1 m.参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84,≈1.73).
(3)从误差的角度考虑,你认为哪个小组的测量过程可以进一步优化 请你设计出优化方案.
22.(13分)在△ABC中,∠ABC=90°.
(1)如图1,分别过A,C两点作经过点B的直线的垂线,垂足分别为点M,N,求证:△ABM∽△BCN;
(2)如图2,P是边BC上一点,∠BAP=∠C,tan∠PAC=,求tan C的值;
(3)如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,sin∠BAC=,=,求tan∠CEB的值.
参考答案与解析
1.C tan 45°=1.
2.B
3.C
4.C ∵AB=AC,∠A=120°,∴∠B=∠C=30°.∵D是BC的中点,∴BD=BC=2,∵DE⊥AB,∴∠BED=90°,∴DE=BD=1.
5.D ∵AC2=12+22=5,AB2=22+42=20,BC2=32+42=25,且AC2+AB2=BC2,∴∠CAB=90°.在Rt△ABC中,cos∠ABC==.
6.A 在Rt△ABC中,∠C=90°,CD是AB边上的中线,∴AB=2CD=2×=17,由勾股定理得BC===8,∴sin A==.
7.C ∵窗户高AB=m米,窗户外面上方0.2米的点C处安装水平遮阳板CD=n米,∴CB=CA+AB=(m+0.2)米.∵光线与水平线成α角,∴∠BDC=α.∵tan∠BDC=,∴CB=n·tan α,∴m=ntan α-0.2.
8.D ∵在Rt△ABC中,AB=5 cm,tan B=,∴AC=3 cm,BC=4 cm.设点D运动t s后,四边形ADEF是菱形,∴DE=AD=t cmCD=(3-t)cm.∵DE∥AB,∴∠ABC=∠DEC,∴sin∠DEC=sin∠ABC==,即=,解得t=.
9.C ∵在△ABC中,AB=AC,∴∠B=∠C.∵∠BAC+∠B+∠C=180°且∠BAC=4∠B,∴6∠B=180°,解得∠B=30°,∴cos B=.如图,过点A作AD⊥BC于点D,设AD=a,则AB=2a,BD=a.∵BC=2BD,∴BC=2a,∴sad∠BAC===,∴cos B·sad∠BAC=×=.
10.B ∵大正方形ABCD的面积是100,∴AD=10.∵小正方形EFGH的面积是4,∴FG=2.由题意得,DF=AG,∴DF-AF=AG-AF=FG=2.设AF=x,则DF=x+2,由勾股定理得,x2+(x+2)2=102,解得x=6(负值已舍去),∴AF=6,DF=8,∴tan∠ADF===.
11.1:2.4 设当自动扶梯向上前进13米时,水平方向前进了x米,根据勾股定理,得x2+52=132,解得x=12(负值已舍去),故该自动扶梯所在斜坡的坡度i=5:12=1:2.4.
12.2 在Rt△ABC中,∠ABC=90°,点D为边AC的中点,BD=2,∴AC=2BD=4,∵∠C=60°,∴∠A=30°,∴BC=AC=2.
13.5 由题意得解得∴∠A=∠B=45°,∴∠C=90°,∴sin A==,∴BC=10sin A=10×=5.
14. sin 75°=sin(45°+30°)=sin 45°cos 30°+cos 45°sin 30°=.
15.10 当AC与AB张开到互相平行时,达到最大夹纸厚度,∴这个长尾夹最大夹纸厚度即为BC的长如图,作AD⊥BC于点D.∵AB=AC=15 mm,∴CD=BD.∵∠ADC=90°,∴=cos∠ACB,∴CD=AC·cos 70°≈15×0.34=5.1(mm),∴BC=2CD≈2×5.1=10.2≈10(mm),∴这个长尾夹最大夹纸厚度约为10 mm.
16.3 解法一 如图1,连接BE交CD于点O.∵四边形BCED是边长为1的正方形∴BE⊥CD,OB=OC=OD=OE=×1=,∴CD=.∵BC∥AD,∴△BCP∽△ADP,∴==,∴CP=CD=,∴OP=OC-CP=-=.在Rt△BOP中,tan∠BPD===3.
解法二 如图2,作DE⊥AB,垂足为点E.在Rt△ABD中,∵AB==
=,AB·DE=AD·BD∴DE=.∵BC∥AD,∴△BCP∽△ADP,∴
==,∴DP=CD==.在Rt△DPE中,PE==,∴tan∠BPD===3.
17.解:(1)原式=3××-()2=-=.(3分)
(2)原式=-=+- =+.(3分)
18.解:(1)如图1所示.(3分)
(2)如图2所示.(6分)
19.解:在△ABC中,∠B=30°,∠C=45°,∴∠BAC=180°-∠B-∠C=105°.
∵EP是AB边的垂直平分线,∴AE=BE,AP=PB=AB=×12=6,EP⊥AB,
∴∠BAE=∠B=30°,∴∠AEF=∠BAE+∠B=60°.
在Rt△BPE中,∵∠BPE=90°,∠B=30°,∴BE===4.(4分)
∵FQ是AC边的垂直平分线,∴FC=FA,∴∠FAC=∠C=45°,
∴∠EAF=∠BAC-∠BAE-∠FAC=105°-30°-45°=30°,
∴∠AFE=180°-∠EAF-∠AEF=180°-30°-60°=90°,
∴EF=AE=BE=2.(9分)
20.解:在Rt△ACO中,∠AOC=180°-∠AOB=30°,AC=10 cm,
∴OA=2AC=20 cm.(4分)
在Rt△A′DO中,∠A′OD=180°-∠A′OB=72°,OA′=OA=20 cm,
∴A′D=A′Osin∠A′OD≈20×0.95=19(cm).(8分)
答:顶部边缘A'处离桌面的高度A'D的长约为19 cm.(9分)
21.解:(1)683.8(2分)
(2)如图,设AB与CD交于点G.
设AG=x m,则在Rt△ACG中,GC==≈≈0.58x(m),(3分)
在Rt△ADG中,GD==≈≈1.19x(m).(4分)
易知四边形CEFD为矩形,∴GC+GD=CD=EF,
∴0.58x+1.19x=683.8,∴x≈386.3.(6分)
386.3+1.8≈388.
答:中原福塔AB的高度约为388 m.(7分)
(3)甲组.
多次测量,结果取平均值.(9分)
22.(1)证明:∵∠M=∠ABC=90°,
∴∠MAB+∠MBA=∠NBC+∠MBA=90°,∴∠MAB=∠NBC.
又∠M=∠N=90°,∴△ABM∽△BCN.(3分)
(2)解:过点P作PM⊥AP,交AC于点M,过点M作MN⊥PC于点N,
如图1,则△PMN∽△APB,∴==tan∠PAC=.(5分)
设PN=2t,则AB=t,
∵∠BAP=∠MPC,∠BAP=∠C,∴∠MPC=∠C,∴CN=PN=2t.
易知△ABP∽△CBA,则=,∴AB2=BP·BC,即(t)2=BP·(BP+4t),
得BP=t(负值已舍去),∴BC=5t,∴tan C==.(8分)
(3)过点A作AH⊥EB于点H,过点C作CK⊥EB,交EB的延长线于点K,则△AHB∽△BKC,CK∥AH,如图2.
∵sin∠BAC=,∴在Rt△ABC中,AB:BC:AC=4:3:5,∴==,==(10分)
∵AE=AB,AH⊥EB,∴EH=BH,∴EK=BH,∴tan∠CEB==·=.(13分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025华师版九年级数学上册
第24章 解直角三角形
时间:90分钟 满分:100分
一、选择题(每小题3分,共30分)
1.tan 45°的值等于( )
A. B. C.1 D.
2.在△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边,下列各式成立的是( )
A.sin B= B.tan B= C.tan B= D.cos B=
3.如图,点A(2,t)在第一象限,OA与x轴所夹锐角为α,tan α=2,则t的值为( )
A.1 B.2 C.4 D.
4.如图,在△ABC中,AB=AC,∠A=120°,D为BC的中点,DE⊥AB于点E,若BC=4,则DE的长为( )
A.1.5 B.2 C.1 D.
5.如图,在4×4的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,则cos∠ABC的值为( )
A. B. C.2 D.
6.在Rt△ABC中,∠C=90°,AC=15,AB边上的中线CD=,则sin A为 ( )
A. B. C. D.
7.如图,已知窗户高AB=m米,窗户外面上方0.2米的点C处安装水平遮阳板CD=n米,当太阳光线与水平线成α角时,光线刚好不能直接射入室内,则m,n的关系式是( )
A.n=m tan α-0.2 B.n=m tan α+0.2
C.m=n tan α-0.2 D.m=n tan α+0.2
8.如图,在Rt△ABC中,∠C=90°,AB=5 cm,tan B=,点D从点A出发沿AC方向以1 cm/s的速度向点C运动.过点D作DE∥AB交BC于点E,过点E作EF⊥BC交AB于点F,当四边形ADEF为菱形时,点D运动的时间为( )
A. s B. s C. s D. s
9.定义:在等腰三角形中,底边与腰的比值叫做顶角的正对,顶角A的正对记作sad A,即sad A=.如图,在△ABC中,AB=AC,∠A=4∠B,则cos B·sad A的值为( )
A.1 B. C. D.
10.我国古代的数学家赵爽在为《周髀算经》作注解时,用4个全等的直角三角形和中间的小正方形拼成一个大正方形,这个图被称为“弦图”,它体现了中国古代数学的成就.如图,已知大正方形ABCD的面积是100,小正方形EFGH的面积是4,那么tan∠ADF=( )
A. B. C.1 D.
二、填空题(每小题3分,共18分)
11.小明站在某商场内的自动扶梯上,当他沿着斜坡向上前进了13米时,他在铅垂方向升高了5米,则该自动扶梯所在的斜坡的坡度i= .
12.如图,在Rt△ABC中,∠ABC=90°,∠C=60°,点D为边AC的中点,BD=
2,则BC的长为 .
13.在△ABC中,∠A,∠B均为锐角,(sin A-1)2+=0,若AB=10,则BC= .
14.对于任意锐角α,β,有等式sin(α+β)=sin α cos β+cos α sin β.结合所学知识,利用上述公式可以求得sin 75°的值是 .(结果保留根号)
15.如图,长尾夹的侧面是△ABC,当AC与AB张开到互相平行时,达到最大夹纸厚度,若AB=AC=15 mm,∠ACB=70°,则该长尾夹最大夹纸厚度约为 mm.(精确到1 mm,参考数据:sin 70°≈0.94,cos 70°≈0.34,tan 70°≈2.75)
16.如图为两个边长为1的正方形组成的2×1格点图,点A,B,C,D都在格点上,AB,CD交于点P,则tan∠BPD= .
三、解答题(共52分)
17.计算:
(1)(3分)3sin 30°·cos 60°-tan230°;
(2)(3分)-cos 30°.
18.(6分)如图,射线OA放置在3×5的正方形网格中,现请你在图中找出格点(即每个小正方形的顶点)B,并连接OB,AB,使△AOB为直角三角形,且
(1)使tan∠AOB的值为1;
(2)使tan∠AOB的值为.
19.(9分)如图,在△ABC中,∠B=30°,∠C=45°,EP是AB边的垂直平分线,FQ是AC边的垂直平分线,连接AE,AF,若AB=12,求EF的长.
20.(9分)2024年6月6日是第29个全国“爱眼日”,某数学兴趣小组开展了“笔记本电脑的张角大小、顶部边缘离桌面的高度与用眼舒适度关系”的实践探究活动.如图,当张角∠AOB=150°时,顶部边缘A处离桌面的高度AC的长为10 cm,此时用眼舒适度不太理想.小组成员调整张角大小继续探究,最后联系黄金比知识,发现当张角∠A'OB=108°时(点A'是点A的对应点),用眼舒适度较为理想,求此时顶部边缘A'处离桌面的高度A'D的长.(精确到1 cm.参考数据:sin 72°≈0.95,cos 72°≈0.31,tan 72°≈3.08)
21.(9分)如图1所示的中原福塔,又名“河南广播电视塔”,是郑州市著名地标之一.五一期间,某数学社团的同学们开展了测量中原福塔高度的实践活动.
【方案设计】
如图2,线段AB表示中原福塔,在中原福塔两侧各选一地测量塔顶的仰角,并测量两地之间的距离.已知测角仪的高CE=DF=1.8 m,测量点E,F与塔底B在同一水平线上.
【测量数据】
甲组同学在E处测得塔顶A的仰角∠ACD=60°,在F处测得塔顶A的仰角∠ADC=40°.
乙组同学三次测量的数据如下.
【问题解决】
(1)三次测得的E,F之间的距离的平均值是 m.
(2)求中原福塔AB的高度(结果精确到1 m.参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84,≈1.73).
(3)从误差的角度考虑,你认为哪个小组的测量过程可以进一步优化 请你设计出优化方案.
22.(13分)在△ABC中,∠ABC=90°.
(1)如图1,分别过A,C两点作经过点B的直线的垂线,垂足分别为点M,N,求证:△ABM∽△BCN;
(2)如图2,P是边BC上一点,∠BAP=∠C,tan∠PAC=,求tan C的值;
(3)如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,sin∠BAC=,=,求tan∠CEB的值.
参考答案与解析
1.C tan 45°=1.
2.B
3.C
4.C ∵AB=AC,∠A=120°,∴∠B=∠C=30°.∵D是BC的中点,∴BD=BC=2,∵DE⊥AB,∴∠BED=90°,∴DE=BD=1.
5.D ∵AC2=12+22=5,AB2=22+42=20,BC2=32+42=25,且AC2+AB2=BC2,∴∠CAB=90°.在Rt△ABC中,cos∠ABC==.
6.A 在Rt△ABC中,∠C=90°,CD是AB边上的中线,∴AB=2CD=2×=17,由勾股定理得BC===8,∴sin A==.
7.C ∵窗户高AB=m米,窗户外面上方0.2米的点C处安装水平遮阳板CD=n米,∴CB=CA+AB=(m+0.2)米.∵光线与水平线成α角,∴∠BDC=α.∵tan∠BDC=,∴CB=n·tan α,∴m=ntan α-0.2.
8.D ∵在Rt△ABC中,AB=5 cm,tan B=,∴AC=3 cm,BC=4 cm.设点D运动t s后,四边形ADEF是菱形,∴DE=AD=t cmCD=(3-t)cm.∵DE∥AB,∴∠ABC=∠DEC,∴sin∠DEC=sin∠ABC==,即=,解得t=.
9.C ∵在△ABC中,AB=AC,∴∠B=∠C.∵∠BAC+∠B+∠C=180°且∠BAC=4∠B,∴6∠B=180°,解得∠B=30°,∴cos B=.如图,过点A作AD⊥BC于点D,设AD=a,则AB=2a,BD=a.∵BC=2BD,∴BC=2a,∴sad∠BAC===,∴cos B·sad∠BAC=×=.
10.B ∵大正方形ABCD的面积是100,∴AD=10.∵小正方形EFGH的面积是4,∴FG=2.由题意得,DF=AG,∴DF-AF=AG-AF=FG=2.设AF=x,则DF=x+2,由勾股定理得,x2+(x+2)2=102,解得x=6(负值已舍去),∴AF=6,DF=8,∴tan∠ADF===.
11.1:2.4 设当自动扶梯向上前进13米时,水平方向前进了x米,根据勾股定理,得x2+52=132,解得x=12(负值已舍去),故该自动扶梯所在斜坡的坡度i=5:12=1:2.4.
12.2 在Rt△ABC中,∠ABC=90°,点D为边AC的中点,BD=2,∴AC=2BD=4,∵∠C=60°,∴∠A=30°,∴BC=AC=2.
13.5 由题意得解得∴∠A=∠B=45°,∴∠C=90°,∴sin A==,∴BC=10sin A=10×=5.
14. sin 75°=sin(45°+30°)=sin 45°cos 30°+cos 45°sin 30°=.
15.10 当AC与AB张开到互相平行时,达到最大夹纸厚度,∴这个长尾夹最大夹纸厚度即为BC的长如图,作AD⊥BC于点D.∵AB=AC=15 mm,∴CD=BD.∵∠ADC=90°,∴=cos∠ACB,∴CD=AC·cos 70°≈15×0.34=5.1(mm),∴BC=2CD≈2×5.1=10.2≈10(mm),∴这个长尾夹最大夹纸厚度约为10 mm.
16.3 解法一 如图1,连接BE交CD于点O.∵四边形BCED是边长为1的正方形∴BE⊥CD,OB=OC=OD=OE=×1=,∴CD=.∵BC∥AD,∴△BCP∽△ADP,∴==,∴CP=CD=,∴OP=OC-CP=-=.在Rt△BOP中,tan∠BPD===3.
解法二 如图2,作DE⊥AB,垂足为点E.在Rt△ABD中,∵AB==
=,AB·DE=AD·BD∴DE=.∵BC∥AD,∴△BCP∽△ADP,∴
==,∴DP=CD==.在Rt△DPE中,PE==,∴tan∠BPD===3.
17.解:(1)原式=3××-()2=-=.(3分)
(2)原式=-=+- =+.(3分)
18.解:(1)如图1所示.(3分)
(2)如图2所示.(6分)
19.解:在△ABC中,∠B=30°,∠C=45°,∴∠BAC=180°-∠B-∠C=105°.
∵EP是AB边的垂直平分线,∴AE=BE,AP=PB=AB=×12=6,EP⊥AB,
∴∠BAE=∠B=30°,∴∠AEF=∠BAE+∠B=60°.
在Rt△BPE中,∵∠BPE=90°,∠B=30°,∴BE===4.(4分)
∵FQ是AC边的垂直平分线,∴FC=FA,∴∠FAC=∠C=45°,
∴∠EAF=∠BAC-∠BAE-∠FAC=105°-30°-45°=30°,
∴∠AFE=180°-∠EAF-∠AEF=180°-30°-60°=90°,
∴EF=AE=BE=2.(9分)
20.解:在Rt△ACO中,∠AOC=180°-∠AOB=30°,AC=10 cm,
∴OA=2AC=20 cm.(4分)
在Rt△A′DO中,∠A′OD=180°-∠A′OB=72°,OA′=OA=20 cm,
∴A′D=A′Osin∠A′OD≈20×0.95=19(cm).(8分)
答:顶部边缘A'处离桌面的高度A'D的长约为19 cm.(9分)
21.解:(1)683.8(2分)
(2)如图,设AB与CD交于点G.
设AG=x m,则在Rt△ACG中,GC==≈≈0.58x(m),(3分)
在Rt△ADG中,GD==≈≈1.19x(m).(4分)
易知四边形CEFD为矩形,∴GC+GD=CD=EF,
∴0.58x+1.19x=683.8,∴x≈386.3.(6分)
386.3+1.8≈388.
答:中原福塔AB的高度约为388 m.(7分)
(3)甲组.
多次测量,结果取平均值.(9分)
22.(1)证明:∵∠M=∠ABC=90°,
∴∠MAB+∠MBA=∠NBC+∠MBA=90°,∴∠MAB=∠NBC.
又∠M=∠N=90°,∴△ABM∽△BCN.(3分)
(2)解:过点P作PM⊥AP,交AC于点M,过点M作MN⊥PC于点N,
如图1,则△PMN∽△APB,∴==tan∠PAC=.(5分)
设PN=2t,则AB=t,
∵∠BAP=∠MPC,∠BAP=∠C,∴∠MPC=∠C,∴CN=PN=2t.
易知△ABP∽△CBA,则=,∴AB2=BP·BC,即(t)2=BP·(BP+4t),
得BP=t(负值已舍去),∴BC=5t,∴tan C==.(8分)
(3)过点A作AH⊥EB于点H,过点C作CK⊥EB,交EB的延长线于点K,则△AHB∽△BKC,CK∥AH,如图2.
∵sin∠BAC=,∴在Rt△ABC中,AB:BC:AC=4:3:5,∴==,==(10分)
∵AE=AB,AH⊥EB,∴EH=BH,∴EK=BH,∴tan∠CEB==·=.(13分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
