第14章 勾股定理单元测试题(含答案)
文档属性
| 名称 | 第14章 勾股定理单元测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 535.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-10 17:54:03 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025华师版数学八年级上学期
第14章 勾股定理
时间:60分钟 满分:100分
一、选择题(每小题3分,共30分)
1.以2,3为直角边的直角三角形的斜边长为( )
A. B. C.4 D.5
2.下列各组数中,以它们为边不能构成直角三角形的是( )
A.3,4,5 B.6,8,10
C.9,12,15 D.5,6,7
3.如图,长方形ABCD中,AB=3,AD=1,点A,B在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于点M,则点M表示的数为( )
A.-1 B. C.-1 D.
4.如图,点E在正方形ABCD的内部,且∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A.80 B.76 C.60 D.48
5.如图,在△ABC中,∠A=90°,DE⊥BC,AB=3,BC=5,EC=2,BD是∠ABC的平分线,则△CDE的周长是( )
A.6 B.7 C.8 D.9
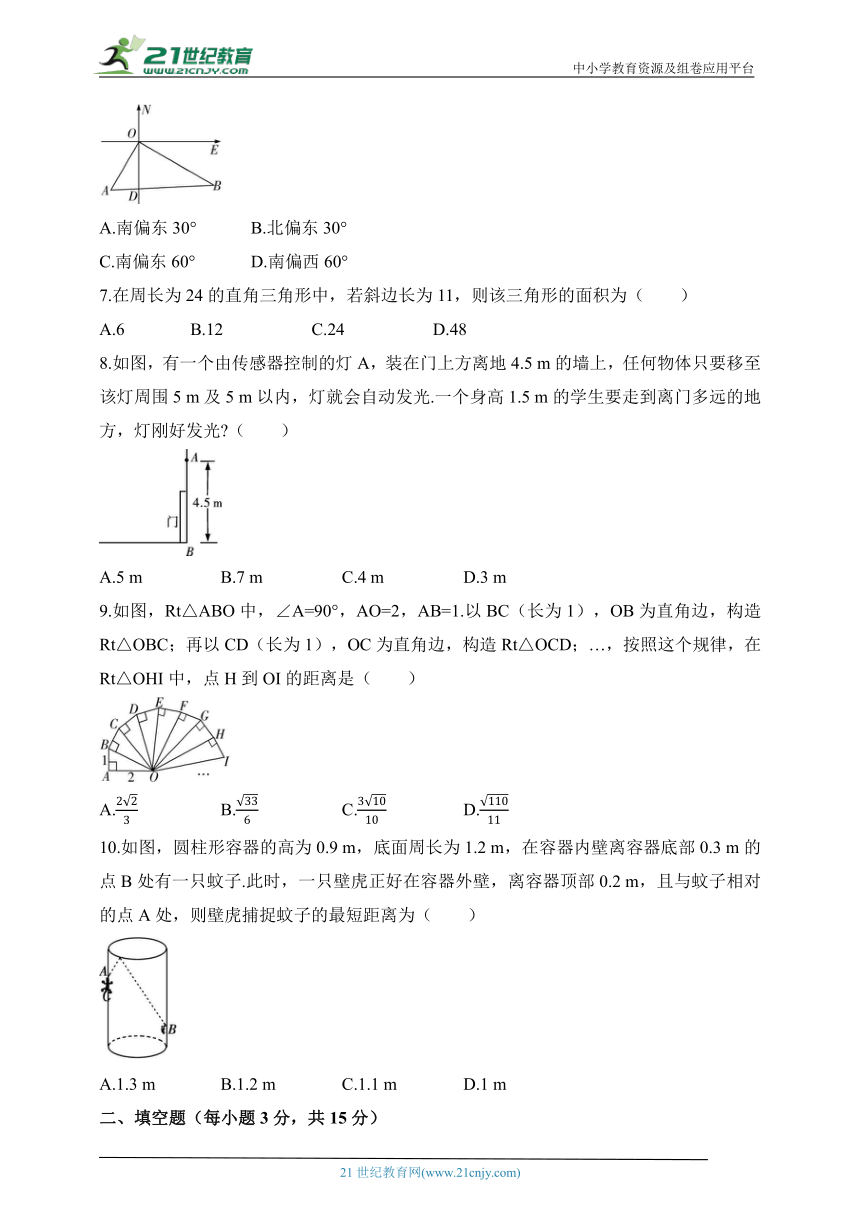
6.如图,两艘航母护卫舰从同一港口O同时出发,一号舰沿南偏西30°方向以12海里/时的速度航行,二号舰以16海里/时的速度航行,离开港口1.5小时后它们分别到达A,B两点,相距30海里,则二号舰航行的方向是( )
A.南偏东30° B.北偏东30°
C.南偏东60° D.南偏西60°
7.在周长为24的直角三角形中,若斜边长为11,则该三角形的面积为( )
A.6 B.12 C.24 D.48
8.如图,有一个由传感器控制的灯A,装在门上方离地4.5 m的墙上,任何物体只要移至该灯周围5 m及5 m以内,灯就会自动发光.一个身高1.5 m的学生要走到离门多远的地方,灯刚好发光 ( )
A.5 m B.7 m C.4 m D.3 m
9.如图,Rt△ABO中,∠A=90°,AO=2,AB=1.以BC(长为1),OB为直角边,构造Rt△OBC;再以CD(长为1),OC为直角边,构造Rt△OCD;…,按照这个规律,在Rt△OHI中,点H到OI的距离是( )
A. B. C. D.
10.如图,圆柱形容器的高为0.9 m,底面周长为1.2 m,在容器内壁离容器底部0.3 m的点B处有一只蚊子.此时,一只壁虎正好在容器外壁,离容器顶部0.2 m,且与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为( )
A.1.3 m B.1.2 m C.1.1 m D.1 m
二、填空题(每小题3分,共15分)
11.木工师傅要做一扇长方形纱窗,做好后量得长为6分米,宽为4分米,对角线为7分米,则这扇纱窗 . (填“合格”或“不合格”)
12.已知a,b,c是△ABC的三边长,且满足+|a-b|=0,则△ABC的形状为 .
13.如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条通过小圆孔到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)的取值范围是 .
14.在我国古代数学著作《九章算术》的第九章《勾股》中记载这样一个问题:“今有开门去阃一尺,不合二寸.问门广几何 ”其大意是:如图,推开两扇门(AD和BC),门边缘上D,C两点到门槛AB的距离都是1尺,两扇门的间隙CD为2寸,则门宽AB是 寸.(1尺=10寸)
15.如图,在△ABC中,AB=AC=5,BC=8,点P是BC边上的动点,过点P分别作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是 .
三、解答题(共55分)
16.(7分)如图,在△ABC中,点D是BC边上一点,连接AD,AB=10,AC=17,BD=6,AD=8.
(1)求∠ADB的度数;
(2)求CD的长.
17.(8分)“儿童散学归来早,忙趁东风放纸鸢”.又到了放风筝的最佳时节,松松同学在学习了“勾股定理”这一章节之后,为了计算如图所示的风筝的垂直高度CE,他测得以下数据:①水平距离BD的长为8米;
②由手中剩余线的长度得出风筝线BC的长为17米;
③牵线放风筝的松松身高1.6米.
(1)求风筝的垂直高度CE;
(2)若松松同学想让风筝沿CD方向下降9米,则他应该往回收线多少米
18.(9分)根据勾股定理知识迁移,完成下列应用.
(1)如图1,分别以直角三角形的三边为直径向外侧作半圆,则它们的面积S1,S2,S3之间满足的等量关系是 ;
(2)应用:如图2,直角三角形的两条直角边长分别为a,b,斜边长为c,分别以三边为直径作半圆.若a=3,c=5,求图中阴影部分的面积.
19.(9分)如图,两个村子A,B在河的同侧,A,B两村到河边CD的距离分别为AC=
1km,BD=3km,已知CD=3km.现要在河边CD上建造一水厂,向A,B两村送自来水.铺设水管的费用为每千米 20 000 元.
(1)请你在CD上确定水厂位置O,使铺设水管的费用最省;
(2)求出(1)中铺设水管的总费用W.
20.(10分)勾股定理神秘而美妙,它的证法多样,其巧妙之处也各有不同,其中的“面积法”给了小聪灵感,他发现:当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明勾股定理.下面是小聪利用图1证明勾股定理的过程:将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:如图1,连接BD,CD,过点D作BC边上的高DF,则DF=EC=b-a.∵S四边形ADCB=S△ACD+S△ABC=b2+ab,S四边形ADCB=S△ADB+S△DCB=c2+a(b-a),∴b2+ab=c2+a(b-a),∴a2+b2=c2.
请参照上述证法,利用图2完成下面的证明:
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
21.(12分)如图,在Rt△ABC中,AB=5 cm,BC=3 cm,∠C=90°.若点P从点A出发,以每秒2 cm的速度沿折线A—C—B—A运动,设运动时间为t s(t>0).
(1)当点P在AC上,且满足PA=PB时,求t的值;
(2)若点P恰好在∠BAC的平分线上,求t的值;
(3)在运动过程中,直接写出当t为何值时,△BCP为等腰三角形,且PC≠BC.
参考答案与解析
1.B
2.D
3.A AC===,则AM=.∵点A表示的数为-1,∴点M表示的数为-1.
4.B 根据勾股定理,得AB2=AE2+BE2=62+82=100,故S正方形ABCD=100.又S△ABE=
×6×8=24,∴S阴影部分=S正方形ABCD-S△ABE=76.
5.A ∵∠A=90°,DE⊥BC,BD是∠ABC的平分线,∴AD=DE.在Rt△ABC中,AC===4,∴△CDE的周长=DE+DC+CE=AD+DC+CE=AC+CE
=4+2=6.
6.C 由题意可得BO=16×1.5=24(海里),AO=12×1.5=18(海里),AB=30海里.∵AO2+BO2=AB2,∴△AOB是直角三角形,∴∠AOB=90°.∵∠AOD=30°,∴∠BOD=60°,∴二号舰的航行方向是南偏东60°.
7.B 设直角三角形的一直角边长为x,另一直角边长为y,由题意可得x+y=24
-11=13,∴(x+y)2=132①.由勾股定理可得x2+y2=112②.由①-②,得2xy=48,∴xy=24,∴该三角形的面积为xy=×24=12.
8.C 如图,设CD表示该学生的身高,点C到点A的距离为5 m,则CD=1.5 m,AC=5 m.过点C作CE⊥AB于点E.由题意可知,BE=CD=1.5 m,∴AE=AB-BE
=4.5-1.5=3(m).在Rt△ACE中,由勾股定理,得CE==4(m),∴BD=CE=4 m,故一个身高1.5 m的学生要走到离门4 m远的地方,灯刚好发光.
9.B 在Rt△ABO中,∠A=90°,AO=2,AB=1,由勾股定理,得OB=
==;在Rt△OBC中,由勾股定理,得OC===;在Rt△OCD中,由勾股定理,得OD=.按照这个规律,在Rt△OHI中,根据勾股定理,得OI==2.如图,过点H作HM⊥OI于点M,则OI·HM=OH·HI,∴×2×HM=××1,∴HM=,∴点H到OI的距离是.
10.D 如图,由题意得,A'D=0.6 m,BD=0.8 m,∴A'B==
=1(m).
11.不合格 ∵42+62=52≠72=49,∴这扇纱窗不是长方形,故不合格.
12.等腰直角三角形 由+|a-b|=0得c2-a2-b2=0,且a-b=0,即a2+b2= c2,a=b,∴△ABC是等腰直角三角形.
13.12≤a≤13 如图,设点O是下底面的中心,点A是下底面的边缘上的一点,点B是上底面的中心,当吸管底部在O点时,吸管在罐内部分a的长度最短,此时a的长等于饮料罐的高,即a=12.当吸管底部在A点时,吸管在罐内部分a的长度最长,此时a的长等于线段AB的长.在Rt△ABO中,AB2=AO2+BO2=
52+122=132,∴AB=13,即a=13.综上,a的长度的取值范围是12≤a≤13.
14.101 如图,过点D作DE⊥AB于点E,则DE=10寸.设单门的宽度AO=x寸,则AE=(x-1)寸.根据勾股定理,得AD2=DE2+AE2,即x2=102+(x-1)2,解得x=50.5,∴AB=101寸.
15.4.8 如图,过点A作AF⊥BC于点F,连接AP.在△ABC中,∵AB=AC=5,BC=8,∴BF=4.在Rt△ABF中,由勾股定理,得AF==3.∵S△ABC=S△ABP
+S△APC,∴×8×3=×5·PD+×5·PE,即12=×5(PD+PE),则PD+PE=4.8.
16.解:(1)∵AB=10,BD=6,AD=8,∴BD2+AD2=62+82=102=AB2,
∴△ABD是直角三角形,∴∠ADB=90°. (3分)
(2)∵∠ADB=90°,∴∠ADC=90°.
在Rt△ACD中,AC=17,AD=8,∴CD==15. (7分)
17.解:(1)在Rt△CDB中,由勾股定理,得CD2=BC2-BD2=172-82=225.
∵CD>0,∴CD=15,∴CE=CD+DE=15+1.6=16.6.
答:风筝的垂直高度CE为16.6米.(3分)
(2)如图,在线段CD上找一点M,使CM=9,则DM=6,连接BM.
在Rt△BDM中,BM===10,则BC-BM=7.
答:他应该往回收线7米.(8分)
18.解:(1)S1+S2=S3 (3分)
设S1,S2,S3对应的直径分别为a,b,c.根据勾股定理,得a2+b2=c2,S1=π()2=a2,同理可得S2=b2,S3=c2,∴S1+S2=a2+b2=(a2+b2)=c2=S3.
(2)设直角三角形的面积为S4.
∵a=3,c=5,∴b===4,∴S4=ab=×3×4=6,
∴阴影部分的面积为S1+S2+S4-S3=S4=6. (9分)
19.解:(1)如图,延长AC到点M,使CM=AC,连接BM交CD于点O,点O就是所选择的位置.(4分)
(2)如图,连接OA,过点M作MN⊥BD,交BD的延长线于点N.(5分)
在Rt△BMN中,BN=BD+DN=4千米,MN=CD=3千米,
∴MB===5(千米),(7分)
∴最短路线AO+BO=MB=5千米,
∴铺设水管的总费用W=5×20 000=100 000(元).
答:最省的铺设水管的总费用是100 000元.(9分)
20.证明:连接BD,过点B作DE边上的高BF,则BF=b-a.(2分)
∵S五边形ACBED=S△ACB+S△ABE+S△ADE=ab+b2+ab,(5分)
S五边形ACBED=S△ACB+S△ABD+S△BDE=ab+c2+a(b-a),(8分)
∴ab+b2+ab=ab+c2+a(b-a),∴a2+b2=c2.(10分)
21.解:(1)∵AB=5 cm,BC=3 cm,∠C=90°,∴AC==4(cm).
由PA=PB,PA=2t cm,可得PB=2t cm,PC=(4-2t)cm.
在Rt△PCB中,PC2+BC2=PB2,即(4-2t)2+32=(2t)2,解得t=,
∴当t=时,PA=PB. (4分)
(2)当点P恰好在∠BAC的平分线上时,如图1.过点P作PE⊥AB于点E,
此时BP=(7-2t)cm,PE=PC=(2t-4)cm,BE=5-4=1(cm).
在Rt△BEP中,PE2+BE2=BP2,即(2t-4)2+12=(7-2t)2,解得t=,
∴当t=时,点P恰好在∠BAC的平分线上.(8分)
(3)当t=或5时,△BCP为等腰三角形,且PC≠BC.(12分)
当点P在AC上时,∵△BCP为等腰三角形,∠ACB=90°,且PC≠BC,∴不存在符合题意的点P.
当点P在AB上时,△BCP为等腰三角形,分为以下两种情况:
①当CP=PB时,如图2,过点P作PF⊥BC于点F,∴BF=BC= cm,
易得PB=AB,即2t-3-4=,解得t=.
②当PB=BC时,2t-3-4=3,解得t=5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025华师版数学八年级上学期
第14章 勾股定理
时间:60分钟 满分:100分
一、选择题(每小题3分,共30分)
1.以2,3为直角边的直角三角形的斜边长为( )
A. B. C.4 D.5
2.下列各组数中,以它们为边不能构成直角三角形的是( )
A.3,4,5 B.6,8,10
C.9,12,15 D.5,6,7
3.如图,长方形ABCD中,AB=3,AD=1,点A,B在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于点M,则点M表示的数为( )
A.-1 B. C.-1 D.
4.如图,点E在正方形ABCD的内部,且∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A.80 B.76 C.60 D.48
5.如图,在△ABC中,∠A=90°,DE⊥BC,AB=3,BC=5,EC=2,BD是∠ABC的平分线,则△CDE的周长是( )
A.6 B.7 C.8 D.9
6.如图,两艘航母护卫舰从同一港口O同时出发,一号舰沿南偏西30°方向以12海里/时的速度航行,二号舰以16海里/时的速度航行,离开港口1.5小时后它们分别到达A,B两点,相距30海里,则二号舰航行的方向是( )
A.南偏东30° B.北偏东30°
C.南偏东60° D.南偏西60°
7.在周长为24的直角三角形中,若斜边长为11,则该三角形的面积为( )
A.6 B.12 C.24 D.48
8.如图,有一个由传感器控制的灯A,装在门上方离地4.5 m的墙上,任何物体只要移至该灯周围5 m及5 m以内,灯就会自动发光.一个身高1.5 m的学生要走到离门多远的地方,灯刚好发光 ( )
A.5 m B.7 m C.4 m D.3 m
9.如图,Rt△ABO中,∠A=90°,AO=2,AB=1.以BC(长为1),OB为直角边,构造Rt△OBC;再以CD(长为1),OC为直角边,构造Rt△OCD;…,按照这个规律,在Rt△OHI中,点H到OI的距离是( )
A. B. C. D.
10.如图,圆柱形容器的高为0.9 m,底面周长为1.2 m,在容器内壁离容器底部0.3 m的点B处有一只蚊子.此时,一只壁虎正好在容器外壁,离容器顶部0.2 m,且与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为( )
A.1.3 m B.1.2 m C.1.1 m D.1 m
二、填空题(每小题3分,共15分)
11.木工师傅要做一扇长方形纱窗,做好后量得长为6分米,宽为4分米,对角线为7分米,则这扇纱窗 . (填“合格”或“不合格”)
12.已知a,b,c是△ABC的三边长,且满足+|a-b|=0,则△ABC的形状为 .
13.如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条通过小圆孔到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)的取值范围是 .
14.在我国古代数学著作《九章算术》的第九章《勾股》中记载这样一个问题:“今有开门去阃一尺,不合二寸.问门广几何 ”其大意是:如图,推开两扇门(AD和BC),门边缘上D,C两点到门槛AB的距离都是1尺,两扇门的间隙CD为2寸,则门宽AB是 寸.(1尺=10寸)
15.如图,在△ABC中,AB=AC=5,BC=8,点P是BC边上的动点,过点P分别作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是 .
三、解答题(共55分)
16.(7分)如图,在△ABC中,点D是BC边上一点,连接AD,AB=10,AC=17,BD=6,AD=8.
(1)求∠ADB的度数;
(2)求CD的长.
17.(8分)“儿童散学归来早,忙趁东风放纸鸢”.又到了放风筝的最佳时节,松松同学在学习了“勾股定理”这一章节之后,为了计算如图所示的风筝的垂直高度CE,他测得以下数据:①水平距离BD的长为8米;
②由手中剩余线的长度得出风筝线BC的长为17米;
③牵线放风筝的松松身高1.6米.
(1)求风筝的垂直高度CE;
(2)若松松同学想让风筝沿CD方向下降9米,则他应该往回收线多少米
18.(9分)根据勾股定理知识迁移,完成下列应用.
(1)如图1,分别以直角三角形的三边为直径向外侧作半圆,则它们的面积S1,S2,S3之间满足的等量关系是 ;
(2)应用:如图2,直角三角形的两条直角边长分别为a,b,斜边长为c,分别以三边为直径作半圆.若a=3,c=5,求图中阴影部分的面积.
19.(9分)如图,两个村子A,B在河的同侧,A,B两村到河边CD的距离分别为AC=
1km,BD=3km,已知CD=3km.现要在河边CD上建造一水厂,向A,B两村送自来水.铺设水管的费用为每千米 20 000 元.
(1)请你在CD上确定水厂位置O,使铺设水管的费用最省;
(2)求出(1)中铺设水管的总费用W.
20.(10分)勾股定理神秘而美妙,它的证法多样,其巧妙之处也各有不同,其中的“面积法”给了小聪灵感,他发现:当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明勾股定理.下面是小聪利用图1证明勾股定理的过程:将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:如图1,连接BD,CD,过点D作BC边上的高DF,则DF=EC=b-a.∵S四边形ADCB=S△ACD+S△ABC=b2+ab,S四边形ADCB=S△ADB+S△DCB=c2+a(b-a),∴b2+ab=c2+a(b-a),∴a2+b2=c2.
请参照上述证法,利用图2完成下面的证明:
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
21.(12分)如图,在Rt△ABC中,AB=5 cm,BC=3 cm,∠C=90°.若点P从点A出发,以每秒2 cm的速度沿折线A—C—B—A运动,设运动时间为t s(t>0).
(1)当点P在AC上,且满足PA=PB时,求t的值;
(2)若点P恰好在∠BAC的平分线上,求t的值;
(3)在运动过程中,直接写出当t为何值时,△BCP为等腰三角形,且PC≠BC.
参考答案与解析
1.B
2.D
3.A AC===,则AM=.∵点A表示的数为-1,∴点M表示的数为-1.
4.B 根据勾股定理,得AB2=AE2+BE2=62+82=100,故S正方形ABCD=100.又S△ABE=
×6×8=24,∴S阴影部分=S正方形ABCD-S△ABE=76.
5.A ∵∠A=90°,DE⊥BC,BD是∠ABC的平分线,∴AD=DE.在Rt△ABC中,AC===4,∴△CDE的周长=DE+DC+CE=AD+DC+CE=AC+CE
=4+2=6.
6.C 由题意可得BO=16×1.5=24(海里),AO=12×1.5=18(海里),AB=30海里.∵AO2+BO2=AB2,∴△AOB是直角三角形,∴∠AOB=90°.∵∠AOD=30°,∴∠BOD=60°,∴二号舰的航行方向是南偏东60°.
7.B 设直角三角形的一直角边长为x,另一直角边长为y,由题意可得x+y=24
-11=13,∴(x+y)2=132①.由勾股定理可得x2+y2=112②.由①-②,得2xy=48,∴xy=24,∴该三角形的面积为xy=×24=12.
8.C 如图,设CD表示该学生的身高,点C到点A的距离为5 m,则CD=1.5 m,AC=5 m.过点C作CE⊥AB于点E.由题意可知,BE=CD=1.5 m,∴AE=AB-BE
=4.5-1.5=3(m).在Rt△ACE中,由勾股定理,得CE==4(m),∴BD=CE=4 m,故一个身高1.5 m的学生要走到离门4 m远的地方,灯刚好发光.
9.B 在Rt△ABO中,∠A=90°,AO=2,AB=1,由勾股定理,得OB=
==;在Rt△OBC中,由勾股定理,得OC===;在Rt△OCD中,由勾股定理,得OD=.按照这个规律,在Rt△OHI中,根据勾股定理,得OI==2.如图,过点H作HM⊥OI于点M,则OI·HM=OH·HI,∴×2×HM=××1,∴HM=,∴点H到OI的距离是.
10.D 如图,由题意得,A'D=0.6 m,BD=0.8 m,∴A'B==
=1(m).
11.不合格 ∵42+62=52≠72=49,∴这扇纱窗不是长方形,故不合格.
12.等腰直角三角形 由+|a-b|=0得c2-a2-b2=0,且a-b=0,即a2+b2= c2,a=b,∴△ABC是等腰直角三角形.
13.12≤a≤13 如图,设点O是下底面的中心,点A是下底面的边缘上的一点,点B是上底面的中心,当吸管底部在O点时,吸管在罐内部分a的长度最短,此时a的长等于饮料罐的高,即a=12.当吸管底部在A点时,吸管在罐内部分a的长度最长,此时a的长等于线段AB的长.在Rt△ABO中,AB2=AO2+BO2=
52+122=132,∴AB=13,即a=13.综上,a的长度的取值范围是12≤a≤13.
14.101 如图,过点D作DE⊥AB于点E,则DE=10寸.设单门的宽度AO=x寸,则AE=(x-1)寸.根据勾股定理,得AD2=DE2+AE2,即x2=102+(x-1)2,解得x=50.5,∴AB=101寸.
15.4.8 如图,过点A作AF⊥BC于点F,连接AP.在△ABC中,∵AB=AC=5,BC=8,∴BF=4.在Rt△ABF中,由勾股定理,得AF==3.∵S△ABC=S△ABP
+S△APC,∴×8×3=×5·PD+×5·PE,即12=×5(PD+PE),则PD+PE=4.8.
16.解:(1)∵AB=10,BD=6,AD=8,∴BD2+AD2=62+82=102=AB2,
∴△ABD是直角三角形,∴∠ADB=90°. (3分)
(2)∵∠ADB=90°,∴∠ADC=90°.
在Rt△ACD中,AC=17,AD=8,∴CD==15. (7分)
17.解:(1)在Rt△CDB中,由勾股定理,得CD2=BC2-BD2=172-82=225.
∵CD>0,∴CD=15,∴CE=CD+DE=15+1.6=16.6.
答:风筝的垂直高度CE为16.6米.(3分)
(2)如图,在线段CD上找一点M,使CM=9,则DM=6,连接BM.
在Rt△BDM中,BM===10,则BC-BM=7.
答:他应该往回收线7米.(8分)
18.解:(1)S1+S2=S3 (3分)
设S1,S2,S3对应的直径分别为a,b,c.根据勾股定理,得a2+b2=c2,S1=π()2=a2,同理可得S2=b2,S3=c2,∴S1+S2=a2+b2=(a2+b2)=c2=S3.
(2)设直角三角形的面积为S4.
∵a=3,c=5,∴b===4,∴S4=ab=×3×4=6,
∴阴影部分的面积为S1+S2+S4-S3=S4=6. (9分)
19.解:(1)如图,延长AC到点M,使CM=AC,连接BM交CD于点O,点O就是所选择的位置.(4分)
(2)如图,连接OA,过点M作MN⊥BD,交BD的延长线于点N.(5分)
在Rt△BMN中,BN=BD+DN=4千米,MN=CD=3千米,
∴MB===5(千米),(7分)
∴最短路线AO+BO=MB=5千米,
∴铺设水管的总费用W=5×20 000=100 000(元).
答:最省的铺设水管的总费用是100 000元.(9分)
20.证明:连接BD,过点B作DE边上的高BF,则BF=b-a.(2分)
∵S五边形ACBED=S△ACB+S△ABE+S△ADE=ab+b2+ab,(5分)
S五边形ACBED=S△ACB+S△ABD+S△BDE=ab+c2+a(b-a),(8分)
∴ab+b2+ab=ab+c2+a(b-a),∴a2+b2=c2.(10分)
21.解:(1)∵AB=5 cm,BC=3 cm,∠C=90°,∴AC==4(cm).
由PA=PB,PA=2t cm,可得PB=2t cm,PC=(4-2t)cm.
在Rt△PCB中,PC2+BC2=PB2,即(4-2t)2+32=(2t)2,解得t=,
∴当t=时,PA=PB. (4分)
(2)当点P恰好在∠BAC的平分线上时,如图1.过点P作PE⊥AB于点E,
此时BP=(7-2t)cm,PE=PC=(2t-4)cm,BE=5-4=1(cm).
在Rt△BEP中,PE2+BE2=BP2,即(2t-4)2+12=(7-2t)2,解得t=,
∴当t=时,点P恰好在∠BAC的平分线上.(8分)
(3)当t=或5时,△BCP为等腰三角形,且PC≠BC.(12分)
当点P在AC上时,∵△BCP为等腰三角形,∠ACB=90°,且PC≠BC,∴不存在符合题意的点P.
当点P在AB上时,△BCP为等腰三角形,分为以下两种情况:
①当CP=PB时,如图2,过点P作PF⊥BC于点F,∴BF=BC= cm,
易得PB=AB,即2t-3-4=,解得t=.
②当PB=BC时,2t-3-4=3,解得t=5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
