小学数学北师大版四下数学好玩作业(含解析)
文档属性
| 名称 | 小学数学北师大版四下数学好玩作业(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 275.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-10 15:06:47 | ||
图片预览


文档简介
小学数学北师大版四下数学好玩作业
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下列图形不能密铺的是( )。
A.正五边形 B.三角形 C.平行四边形
2.周日,芳芳主动帮妈妈做家务:扫地7分,擦拭家具10分,用洗衣机洗衣服20分,晾衣服4分。经过合理安排,做完这些事至少要花( )分。
A.21 B.24 C.30 D.31
3.下列不能密铺的图形是( )。
A. B. C.
4.李老师装修房子,打算用下面的直角三角形瓷砖贴满正方形的电视墙(如下图)。请你想一想,空白部分还需要( )块这样的瓷砖。
A.6 B.8 C.10 D.12
5.一口锅一次可煎两张饼,饼的两面都要煎,煎一面需要2分钟,煎完3张饼至少需要( )分钟。
A.12 B.8 C.6
二、填空题
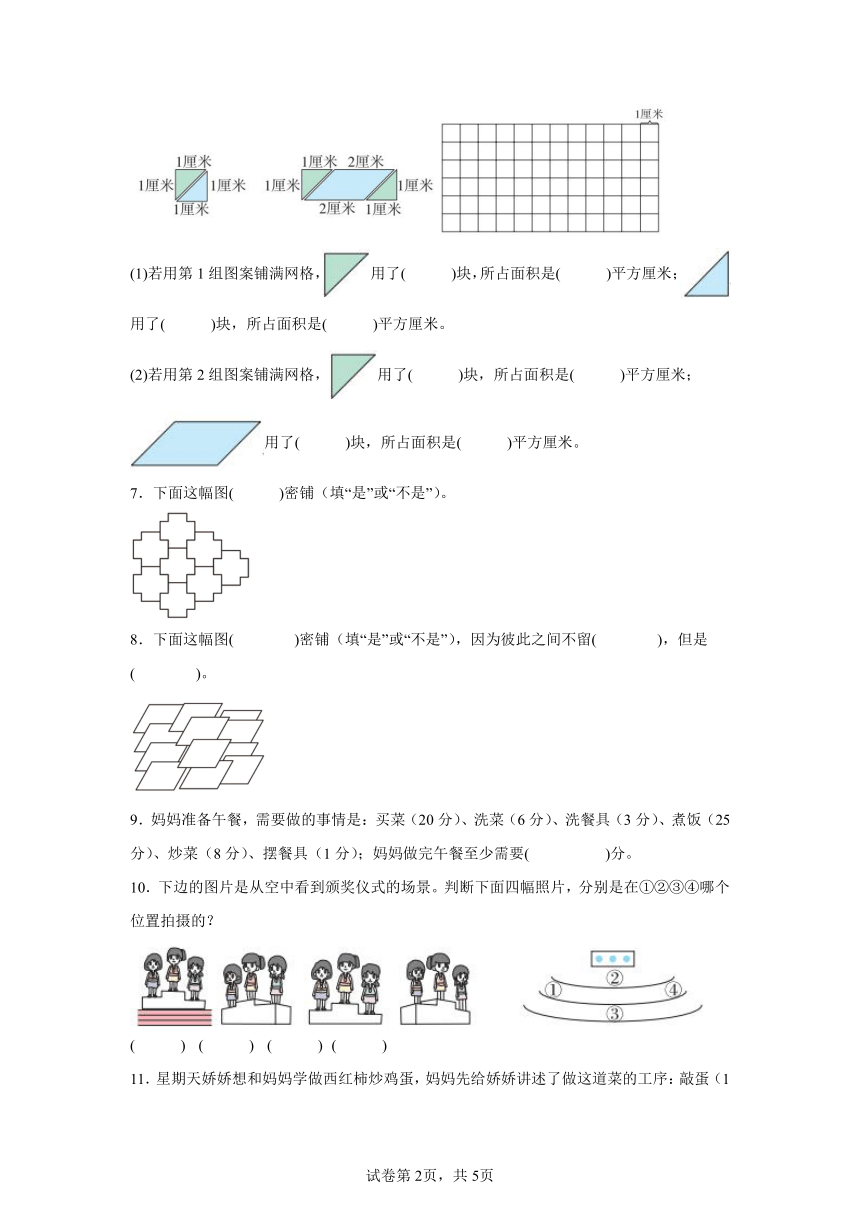
6.小小设计师。(请从下面两组瓷砖中选用一组设计一个图案)
(1)若用第1组图案铺满网格,用了( )块,所占面积是( )平方厘米;用了( )块,所占面积是( )平方厘米。
(2)若用第2组图案铺满网格,用了( )块,所占面积是( )平方厘米;用了( )块,所占面积是( )平方厘米。
7.下面这幅图( )密铺(填“是”或“不是”)。
8.下面这幅图( )密铺(填“是”或“不是”),因为彼此之间不留( ),但是( )。
9.妈妈准备午餐,需要做的事情是:买菜(20分)、洗菜(6分)、洗餐具(3分)、煮饭(25分)、炒菜(8分)、摆餐具(1分);妈妈做完午餐至少需要( )分。
10.下边的图片是从空中看到颁奖仪式的场景。判断下面四幅照片,分别是在①②③④哪个位置拍摄的?
( ) ( ) ( ) ( )
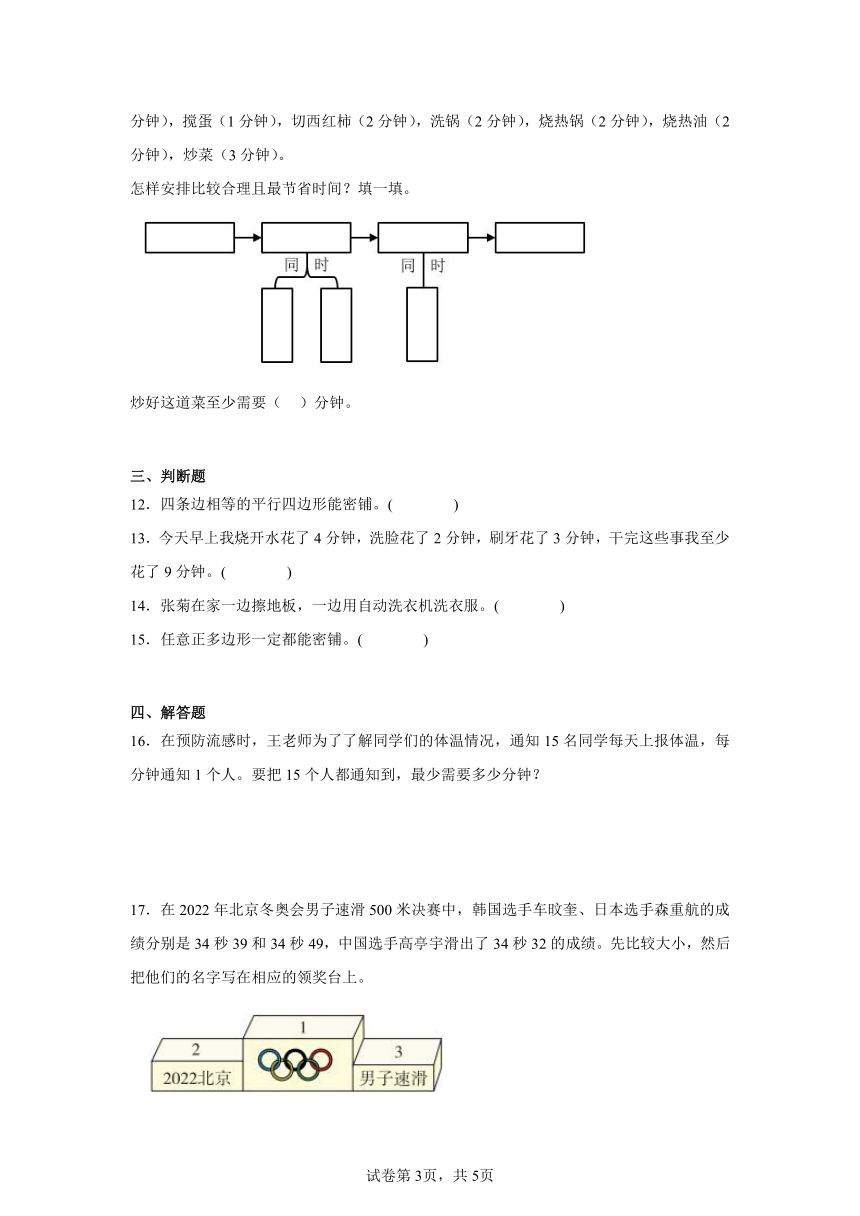
11.星期天娇娇想和妈妈学做西红柿炒鸡蛋,妈妈先给娇娇讲述了做这道菜的工序:敲蛋(1分钟),搅蛋(1分钟),切西红柿(2分钟),洗锅(2分钟),烧热锅(2分钟),烧热油(2分钟),炒菜(3分钟)。
怎样安排比较合理且最节省时间?填一填。
炒好这道菜至少需要( )分钟。
三、判断题
12.四条边相等的平行四边形能密铺。( )
13.今天早上我烧开水花了4分钟,洗脸花了2分钟,刷牙花了3分钟,干完这些事我至少花了9分钟。( )
14.张菊在家一边擦地板,一边用自动洗衣机洗衣服。( )
15.任意正多边形一定都能密铺。( )
四、解答题
16.在预防流感时,王老师为了了解同学们的体温情况,通知15名同学每天上报体温,每分钟通知1个人。要把15个人都通知到,最少需要多少分钟?
17.在2022年北京冬奥会男子速滑500米决赛中,韩国选手车旼奎、日本选手森重航的成绩分别是34秒39和34秒49,中国选手高亭宇滑出了34秒32的成绩。先比较大小,然后把他们的名字写在相应的领奖台上。
18.某旅社新“推出某某风景区一日游”。
成人票:240元/人 儿童票:130元/人 团体票(大于等于7人):180元/人
(1)儿童4人,成人6人,怎样买票合算?花多少钱?
(2)儿童6人,成人4人,怎样买票合算?花多少钱?
19.“自力更生、艰苦创业、团结协作、无私奉献”的红旗渠精神,是中华民族伟大精神的生动体现,是我们党的宝贵精神财富。为更好的学习、传承这种精神,花园小学组织同学们到红旗渠教育实践基地进行“红色研学”活动。参加这次活动的老师有18人,学生有352人。如果租车前往,怎样租车最省钱呢?
车型 小车 大车
限乘人数/人 36 60
租金/元 800 1200
20.某商场要把82吨货物从商场运往车站,现有大卡车和小卡车两种运输工具可供选择。
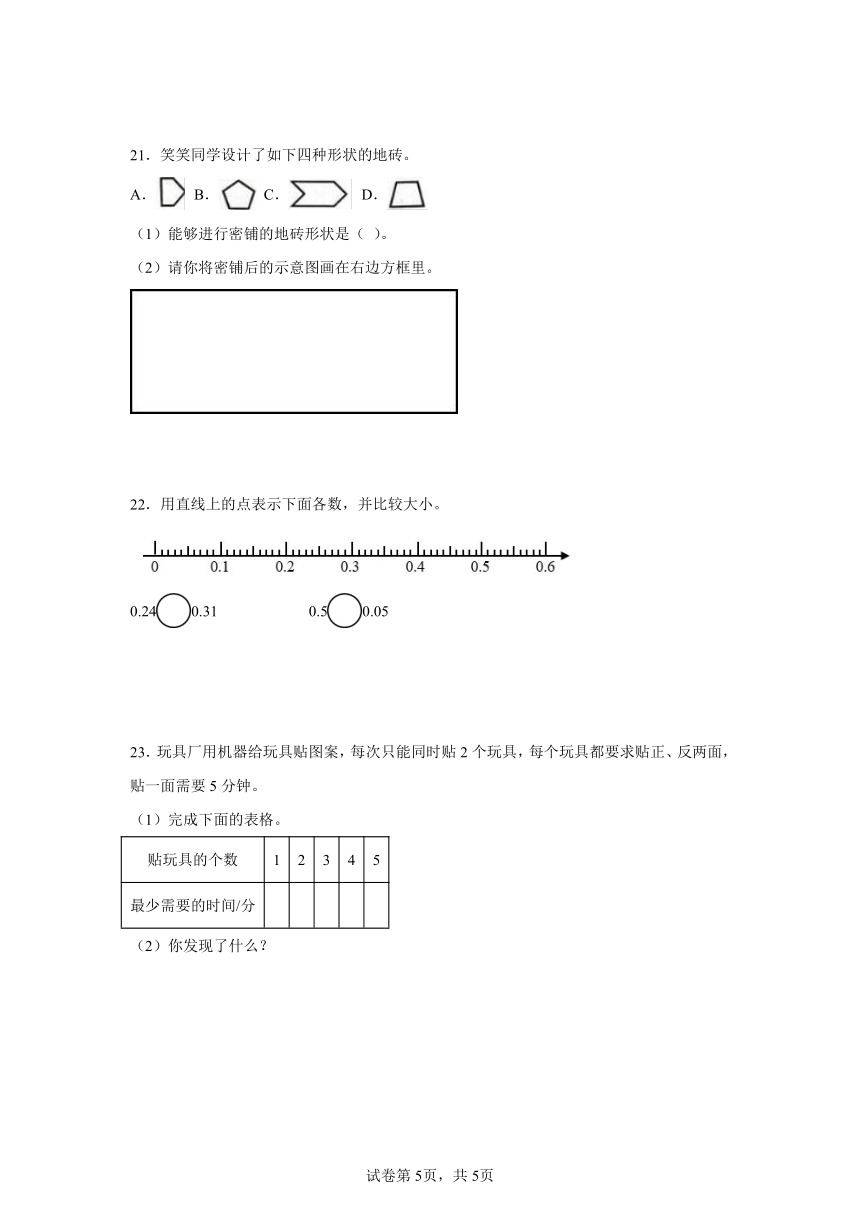
21.笑笑同学设计了如下四种形状的地砖。
A. B. C. D.
(1)能够进行密铺的地砖形状是( )。
(2)请你将密铺后的示意图画在右边方框里。
22.用直线上的点表示下面各数,并比较大小。
0.240.31 0.50.05
23.玩具厂用机器给玩具贴图案,每次只能同时贴2个玩具,每个玩具都要求贴正、反两面,贴一面需要5分钟。
(1)完成下面的表格。
贴玩具的个数 1 2 3 4 5
最少需要的时间/分
(2)你发现了什么?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】用形状、大小完全相同的几种或几十种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺,能密铺的图形在一个拼接点处的特点是:几个图形的内角拼接在一起时,其和等于360°,并使相等的边互相重合,据此选择即可。
【详解】A.正五边形不可以密铺,选项错误;
B.三角形内角和180°,可以密铺,选项正确;
C.平行四边形内角和为360°,可以密铺,选项正确。
图形不能密铺的是正五边形。
故答案为:A
2.B
【分析】
先观察做事情的顺序,考虑哪些事情可以同时做,写出做事情的顺序,计算所需时间。
【详解】洗衣服20分(洗衣服的同时可以扫地和擦拭家居),晾衣服4分。
20+4=24(分)
经过合理安排,做完这些事至少要花24分。
故答案为:B
3.C
【分析】图形之间没有空隙,也不重复,这种铺法在数学上叫图形的密铺,也叫图形的镶嵌。
【详解】A.等边三角形三个角都相等,每个角都是60°,在每个拼接点处正好能容纳6个内角。所以三角形可以密铺。
B.正六边形可以密铺,因为它的每个内角都是120°,在每个拼接点处正好能容纳3个内角。所以正六边形也可以密铺。
C.正五边形不可以密铺,因为它的每个内角都是108°,而360°不是108°的整数倍,在每个拼接点处的内角不能保证没有空隙或没有重叠现象。所以正五边形不可以密铺。
故答案为:C
4.D
【分析】如图所示,两个直角三角形可以拼成一个长80厘米宽40厘米的长方形。四个直角三角形可以拼成边长为80厘米的正方形。空白部分可以分成4个长80厘米宽40厘米的长方形,以及一个长80厘米的正方形。则一共需要(2×4+4)个直角三角形。
【详解】2×4+4
=8+4
=12(块)
空白部分还需要12块这样的瓷砖。
故答案为:D
5.C
【分析】一口锅一次可煎两张饼,饼有两面,煎完一面要2分钟,第一次放第1张的第一面和第2张的第一面,第二次放第1张的第二面和第3张的第一面,第三次放第2张的第二面和第3张的第二面,一共要花3个2分钟,据此计算。
【详解】3×2=6(分钟)
煎完3张饼至少需要6分钟。
故答案选:C
6.(1) 72 36 72 36
(2) 48 24 24 48
【分析】(1)用第一组图案中的,则每个小正方形的上半部分都需要一块,求出有多少个小正方形,即有多少个,进而即可得到面积; 用第一组图案中的,则每个小正方形的上半部分都需要一块,求出有多少个小正方形,即有多少个,进而即可得到面积。
(2)用第二组图案中的,则每3厘米用两个,据此即可求出有多少块,进而求得面积;用第二组图案中的,则每3厘米用一个,据此即可求出有多少块,进而求得面积。
【详解】(1)若用第1组图案,用了12×6=72块,所占面积是72÷2=36平方厘米,用了72块,所占面积是36平方厘米。
(2)若用第2组图案,用了8×6=48块,所占面积是48÷2=24平方厘米,用了4×6=24块,所占面积是24×2=48平方厘米。
7.是
【分析】平面图形密铺的特点:(1)用一种或几种全等图形进行拼接;(2)拼接处不留缝隙,不重叠;(3)连续铺成一片;据此判断。
【详解】此图即不留缝隙,也不重叠的铺满,所以这幅图是密铺。
【点睛】
8. 不是 空隙 重叠
【分析】
用一种或几种全等图形(规则图形或不规则图形)进行拼接,图形之间没有空隙,也不重复,这种铺法在数学上叫图形的密铺,也叫图形的镶嵌。图形之间没有空隙,也不重叠,是密铺。据此解答。
【详解】观察图形,平行四边形之间确实没留空隙,但是相互之间有重叠,所以不是密铺。故这幅图不是密铺,因为彼此之间不留空隙,但是重叠。
9.45
【分析】先买菜(20分钟),然后在煮饭25分钟内,可以同步完成洗菜(6分钟)+洗餐具(3分钟)+炒菜(8分钟)+摆餐具(1分钟),这样做完午餐至少需要的时间是买菜加上煮饭的时间;据此解答。
【详解】20+25=45(分钟)
即妈妈准备午餐,需要做的事情是:买菜(20分)、洗菜(6分)、洗餐具(3分)、煮饭(25分)、炒菜(8分)、摆餐具(1分).妈妈做完午餐至少需要45分钟。
10. ③ ④ ② ①
【分析】观察图形可知,第一幅图是从正面拍摄的 ,第二幅图是从右面拍摄的,第三幅图是从正面拍摄的,比第一幅图从正面拍摄的位置稍近一些,第四幅图是从左面拍摄的,据此结合图片中的位置进行判断即可。
【详解】第一幅图在③号位置拍摄,第二幅图在④号位置拍摄,第三幅图在②号位置拍摄,第四幅图在①号位置拍摄。
11.见详解
9
【分析】要使需要的时间最短,应先洗锅,然后烧热锅,在烧热锅的同时,可进行敲蛋和搅蛋。然后烧热油,在烧热油的同时,可进行切西红柿,最后炒菜。一共需要(2+2+2+3)分钟。
【详解】2+2+2+3=9(分钟)
炒好这道菜至少需要9分钟。
【点睛】本题考查优化问题,要想时间最短,应合理安排各项任务之间的顺序,注意同时进行的两项任务应互不干扰。
12.√
【分析】用形状、大小完全相同的图形进行拼接,如果能没有空隙、又不重叠地铺在同一个平面上,这种铺法就叫作“密铺”。能够密铺的图形特征是内角之和是360°。
【详解】四条边相等的平行四边形的两个锐角和两个钝角加起来恰好是360°,所以能密铺。
故答案为:√
【点睛】本题考查了密铺,掌握密铺的前提条件是解题的关键。
13.×
【分析】烧开水的同时,可以洗脸或者刷牙,需要(2+3)分钟 。
【详解】2+3=5(分)
故答案为:×
【点睛】此题属于合理安排时间问题,要本着既节约时间又不使每道工序相矛盾进行解答。
14.√
【分析】因为用自动洗衣机洗衣服可以腾出手完成擦地板的工作,所以张菊在家可以一边擦地板,一边用自动洗衣机洗衣服。
【详解】根据分析可知:
张菊在家一边擦地板,一边用自动洗衣机洗衣服,原题说法正确。
故答案为:√
【点睛】此题属于合理安排时间问题,要本着既节约时间又不使每道工序相矛盾进行解答。
15.×
【分析】平面图形密铺的特点:(1)用一种或几种全等图形进行拼接;(2)拼接处不留空隙、不重叠;(3)连续铺成一片。根据正多边形的组合能否密铺,关键是看位于同一顶点处的几个角之和能否为360°,如果能组成360°就能够密铺,反之不能。
【详解】反例:
正五边形每个内角是180°-360°÷5
=180°-72°
=108°
108°不能整除360°,不能密铺,所以任意正多边形一定都能密铺的说法错误。
故答案为:×
【点睛】本题考查平面图形的密铺。根据密铺的意义,掌握常见的密铺图形和不能密铺的图形种类是解题的关键。
16.4分钟
【分析】
王老师先通知一位同学,再和这位同学一起各再通知一位同学,所有接到通知的同学和王老师继续同时去通知其他同学,据此分析。
【详解】
第1分钟:1名
第2分钟:1+2=3(名)
第3分钟:3+4=7(名)
第4分钟:7+8=15(名)
答:最少需要4分钟。
17.见详解
【分析】
在速滑比赛中滑行的长度相同时,用的时间越少,则表示越靠前,比较三人滑行时间即可确定冠军、亚军和季军。
【详解】
34秒49>34秒39>34秒32
答:冠军是高亭宇,亚军是车旼奎,季军是森重航。
18.(1)买7张团体票和3张儿童票合算,花1650元钱;(2)买7张团体票和3张儿童票合算,花1650元钱
【分析】(1)①可以买6张成人票和4张儿童票。因为儿童票的单价小于团体票的单价,所以儿童应尽量买儿童票,那么还可以买7张团体票和3张儿童票。分别算出每种购买方式的总价,然后对它们的总价进行比较,花费最少的就是最合算的。
(2)可以买4张成人票和6张儿童票,或买7张团体票和3张儿童票。分别算出每种购买方式的总价,然后对它们的总价进行比较,花费最少的就是最合算的。
【详解】(1)购买方式一:6张成人票和4张儿童票
6×240+4×130
=1440+520
=1960(元)
购买方式二:7张团体票和3张儿童票
7×180+3×130
=1260+390
=1650(元)
1960>1650
答:买7张团体票和3张儿童票合算,花1650元钱。
(2)购买方式一:4张成人票和6张儿童票
4×240+6×130
=960+780
=1740(元)
购买方式二:7张团体票和3张儿童票
7×180+3×130
=1260+390
=1650(元)
1740>1650
答:买7张团体票和3张儿童票合算,花1650元钱。
19.见详解
【分析】先求出师生的总人数,把352与18相加,得总人数是370人。
方案一:全部租大车,计算出需要几辆大车,用总人数除以60,因为有余数,所以给商加1即为需要租车的数量,7乘60求出可以乘坐的总人数,再用车的数量乘1200即可求出总费用。
方案二:减少大车的数量,大车租6辆,其余的人租小车坐,6辆大车可以坐360人,其余的人坐小车,6乘60,所得积加36即可求出可以乘坐的总人数,再用1200乘6,所得积加800可以求出需要的总费用。
方案三:在方案二的基础上,减少大车的数量1辆,小船需要1辆,按照同样的计算方法求出总的费用,以及可以乘坐的总人数;
方案四:在方案三的基础上大车减少1辆,计算出大车可以乘坐的总人数,再用370减这个总人数,即可求出剩下的人数,再用这个人数除以36,若有余数,给商加1即为需要租小车的数量,给60乘大车数量,给36乘小车数量,再把两个积相加,即可求出可以乘坐的总人数,给大车数量乘1200,给小车数量乘800,最后相加即可求出需要租车的总费用;
方案五:在方案四的基础上大车减少1辆,计算出大车可以乘坐的总人数,用370减这个数可以求出剩下多少人,再用这个人数除以36,若有余数,给商加1即为需要租小车的数量,给60乘大车数量,给36乘小车数量,再把两个积相加,即可求出可以乘坐的总人数,给大车数量乘1200,给小车数量乘800,最后相加即可求出需要租车的总费用;
方案六:在方案五的基础上大车减少1辆,计算出大车可以乘坐的总人数,用370减这个数可以求出剩下多少人,再用这个人数除以36,若有余数,给商加1即为需要租小车的数量,给60乘大车数量,给36乘小车数量,再把两个积相加,即可求出可以乘坐的总人数,给大车数量乘1200,给小车数量乘800,最后相加即可求出需要租车的总费用;
方案七:在方案六的基础上大车减少1辆,计算出大车可以乘坐的总人数,用370减这个数可以求出剩下多少人,再用这个人数除以36,若有余数,给商加1即为需要租小车的数量,给60乘大车数量,给36乘小车数量,再把两个积相加,即可求出可以乘坐的总人数,给大车数量乘1200,给小车数量乘800,最后相加即可求出需要租车的总费用;
方案八:全部租小车,用总人数370除以36求出要租几辆小车还剩几人,再用商加1求需要租小车的数量,要求可以乘坐多少人,给小车的数量乘36即可,求费用把小车的数量与800相乘即可。
【详解】352+18=370(人)
方案一:全部租大车,370÷60=6(辆)……10(人)
6+1=7(辆)
1200×7=8400(元)
方案二:7-1=6(辆)
370-60×6
=370-360
=10(人)
6×60+36
=360+36
=396(人)
1200×6+800
=7200+800
=8000(元)
方案三:6-1=5(辆)
370-60×5
=370-300
=70(人)
70÷36=1(辆)……34(人)
1+1=2(辆)
36×2+60×5
=72+300
=372(人)
800×2+1200×5
=1600+6000
=7600(元)
方案四:5-1=4(辆)
370-60×4
=370-240
=130(人)
130÷36=3(辆)……22(人)
3+1=4(辆)
36×4+60×4
=144+240
=384(人)
800×4+1200×4
=3200+4800
=8000(元)
方案五:4-1=3(辆)
370-60×3
=370-180
=190(人)
190÷36=5(辆)……10(人)
5+1=6(辆)
36×6+60×3
=216+180
=396(人)
800×6+1200×3
=4800+3600
=8400(元)
方案六:3-1=2(辆)
370-60×2
=370-120
=250(人)
250÷36=6(辆)……34(人)
6+1=7(辆)
36×7+60×2
=252+120
=372(人)
800×7+1200×2
=5600+2400
=8000(元)
方案七:2-1=1(辆)
370-60=310(人)
310÷36=8(辆)……22(人)
8+1=9(辆)
36×9+60
=324+60
=384(人)
800×9+1200
=7200+1200
=8400(元)
方案八:370÷36=10(辆)……10(人)
10+1=11(辆)
11×36=396(人)
11×800=8800(元)
方案 大车/辆 小车/辆 可坐人数/人 总费用/元
方案一 7 0 420 8400
方案二 6 1 396 8000
方案三 5 2 372 7600
方案四 4 4 384 8000
方案五 3 6 396 8400
方案六 2 7 372 8000
方案七 1 9 384 8400
方案八 0 11 396 8800
答:租5辆大车和2辆小车最划算。
【点睛】根据1辆车可以乘坐的人数×车的数量,来求可以乘坐的总人数,根据租1辆车的费用×车的数量来求租车的费用。
20.一共租7辆大卡车和3辆小卡车运费最低,总运费为1670元
【分析】先算出大卡车运输每吨货物的运费为:200÷10=20(元),小卡车运输每吨货物的运费为:90÷4=22.5(元),因为22.5>20,所以选择尽可能多的大卡车并且车能得到完全利用,更划算点;第一种方案:租用大卡车8辆,小卡车1辆,总运费为:200×8+90=1690(元);第二种方案为:租用大卡车7辆,小卡车3辆,总运费为:200×7+90×3=1670(元);第三种方案为:租用大卡车6辆,小卡车6辆,总运费为:200×6+90×6=1740(元);因为1670<1690<1740,所以一共租7辆大卡车和3辆小卡车运费最低,总运费为1670元。
【详解】由分析可知:
租用大卡车7辆,小卡车3辆
总运费为:200×7+90×3
=1400+270
=1670(元)
答:一共租7辆大卡车和3辆小卡车运费最低,总运费为1670元。
【点睛】本题考查优化问题,需先算出大卡车和小卡车每吨的运费,看尽量多用哪种车运输更划算,还要考虑车是否得到完全利用。
21.(1)A、C、D;
(2)见详解
【分析】(1)用一种或几种全等图形(规则图形或不规则图形)进行拼接,图形之间没有空隙,也不重复,这种铺法在数学上叫图形的密铺,也叫图形的镶嵌。任何弧线图形不能密铺;除正三角形、正四边形和正六边形外,其他正多边形都不可以密铺平面;所有任意三角形与任意四边形都可以密铺。
(2)观察地砖的形状,先铺一铺,看平铺时砖块之间是否有空隙或砖块是否重叠,把密铺后的图形画在方框里即可。
【详解】(1)能够进行密铺的地砖形状是(A、C、D)。
(2)如图:
【点睛】本题考查平面图形的密铺。根据密铺的意义,掌握常见的密铺图形和不能密铺的图形种类是解题的关键。
22.画图见详解
<;>
【分析】直线上一大格表示0.1,一小格表示0.01,据此表示出0.24,0.31,0.5,0.05。小数比较大小时,先看它们的整数部分,整数部分大的那个数就大;如果整数部分相同,十分位上的数大的那个数就大;如果十分位上的数相同,百分位上的数大的那个数就大……
【详解】
0.24<0.31 0.5>0.05
【点睛】本题考查小数的意义以及小数比较大小的方法,小数比较大小的方法与整数基本相同,都是从高位起,依次把相同数位上的数进行比较。
23.(1)10;10;15;20;25
(2)见详解
【分析】若贴1个玩具,需要2个5分钟,即(2×5)分钟。若贴2个玩具,也需要2个5分钟,即(2×5)分钟。若贴3个玩具,假设这3个玩具分别为a、b、c;第一次贴a、b的正面;第二次贴a的反面和c的正面;第三次贴b、c的反面。所以贴3个玩具需要(3×5)分钟。若贴4个玩具,可以分成2组,每组2个玩具,需要(2×2×5)分钟。若贴5个玩具,可以分成2组,一组2个玩具,一组3个玩具,需要(2×5+3×5)分钟。
【详解】(1)2×5=10(分钟)
3×5=15(分钟)
4÷2×10
=2×10
=20(分钟)
2×5+3×5
=10+15
=25(分钟)
贴玩具的个数 1 2 3 4 5
最少需要的时间/分 10 10 15 20 25
(2)当贴玩具的个数大于或等于2个时,贴玩具的个数×贴一面的时间=最少需要的时间。
【点睛】在优化问题中,要统筹安排贴图案的顺序,使机器里始终没有空位,这样才能保证需要的时间最短。
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下列图形不能密铺的是( )。
A.正五边形 B.三角形 C.平行四边形
2.周日,芳芳主动帮妈妈做家务:扫地7分,擦拭家具10分,用洗衣机洗衣服20分,晾衣服4分。经过合理安排,做完这些事至少要花( )分。
A.21 B.24 C.30 D.31
3.下列不能密铺的图形是( )。
A. B. C.
4.李老师装修房子,打算用下面的直角三角形瓷砖贴满正方形的电视墙(如下图)。请你想一想,空白部分还需要( )块这样的瓷砖。
A.6 B.8 C.10 D.12
5.一口锅一次可煎两张饼,饼的两面都要煎,煎一面需要2分钟,煎完3张饼至少需要( )分钟。
A.12 B.8 C.6
二、填空题
6.小小设计师。(请从下面两组瓷砖中选用一组设计一个图案)
(1)若用第1组图案铺满网格,用了( )块,所占面积是( )平方厘米;用了( )块,所占面积是( )平方厘米。
(2)若用第2组图案铺满网格,用了( )块,所占面积是( )平方厘米;用了( )块,所占面积是( )平方厘米。
7.下面这幅图( )密铺(填“是”或“不是”)。
8.下面这幅图( )密铺(填“是”或“不是”),因为彼此之间不留( ),但是( )。
9.妈妈准备午餐,需要做的事情是:买菜(20分)、洗菜(6分)、洗餐具(3分)、煮饭(25分)、炒菜(8分)、摆餐具(1分);妈妈做完午餐至少需要( )分。
10.下边的图片是从空中看到颁奖仪式的场景。判断下面四幅照片,分别是在①②③④哪个位置拍摄的?
( ) ( ) ( ) ( )
11.星期天娇娇想和妈妈学做西红柿炒鸡蛋,妈妈先给娇娇讲述了做这道菜的工序:敲蛋(1分钟),搅蛋(1分钟),切西红柿(2分钟),洗锅(2分钟),烧热锅(2分钟),烧热油(2分钟),炒菜(3分钟)。
怎样安排比较合理且最节省时间?填一填。
炒好这道菜至少需要( )分钟。
三、判断题
12.四条边相等的平行四边形能密铺。( )
13.今天早上我烧开水花了4分钟,洗脸花了2分钟,刷牙花了3分钟,干完这些事我至少花了9分钟。( )
14.张菊在家一边擦地板,一边用自动洗衣机洗衣服。( )
15.任意正多边形一定都能密铺。( )
四、解答题
16.在预防流感时,王老师为了了解同学们的体温情况,通知15名同学每天上报体温,每分钟通知1个人。要把15个人都通知到,最少需要多少分钟?
17.在2022年北京冬奥会男子速滑500米决赛中,韩国选手车旼奎、日本选手森重航的成绩分别是34秒39和34秒49,中国选手高亭宇滑出了34秒32的成绩。先比较大小,然后把他们的名字写在相应的领奖台上。
18.某旅社新“推出某某风景区一日游”。
成人票:240元/人 儿童票:130元/人 团体票(大于等于7人):180元/人
(1)儿童4人,成人6人,怎样买票合算?花多少钱?
(2)儿童6人,成人4人,怎样买票合算?花多少钱?
19.“自力更生、艰苦创业、团结协作、无私奉献”的红旗渠精神,是中华民族伟大精神的生动体现,是我们党的宝贵精神财富。为更好的学习、传承这种精神,花园小学组织同学们到红旗渠教育实践基地进行“红色研学”活动。参加这次活动的老师有18人,学生有352人。如果租车前往,怎样租车最省钱呢?
车型 小车 大车
限乘人数/人 36 60
租金/元 800 1200
20.某商场要把82吨货物从商场运往车站,现有大卡车和小卡车两种运输工具可供选择。
21.笑笑同学设计了如下四种形状的地砖。
A. B. C. D.
(1)能够进行密铺的地砖形状是( )。
(2)请你将密铺后的示意图画在右边方框里。
22.用直线上的点表示下面各数,并比较大小。
0.240.31 0.50.05
23.玩具厂用机器给玩具贴图案,每次只能同时贴2个玩具,每个玩具都要求贴正、反两面,贴一面需要5分钟。
(1)完成下面的表格。
贴玩具的个数 1 2 3 4 5
最少需要的时间/分
(2)你发现了什么?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】用形状、大小完全相同的几种或几十种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺,能密铺的图形在一个拼接点处的特点是:几个图形的内角拼接在一起时,其和等于360°,并使相等的边互相重合,据此选择即可。
【详解】A.正五边形不可以密铺,选项错误;
B.三角形内角和180°,可以密铺,选项正确;
C.平行四边形内角和为360°,可以密铺,选项正确。
图形不能密铺的是正五边形。
故答案为:A
2.B
【分析】
先观察做事情的顺序,考虑哪些事情可以同时做,写出做事情的顺序,计算所需时间。
【详解】洗衣服20分(洗衣服的同时可以扫地和擦拭家居),晾衣服4分。
20+4=24(分)
经过合理安排,做完这些事至少要花24分。
故答案为:B
3.C
【分析】图形之间没有空隙,也不重复,这种铺法在数学上叫图形的密铺,也叫图形的镶嵌。
【详解】A.等边三角形三个角都相等,每个角都是60°,在每个拼接点处正好能容纳6个内角。所以三角形可以密铺。
B.正六边形可以密铺,因为它的每个内角都是120°,在每个拼接点处正好能容纳3个内角。所以正六边形也可以密铺。
C.正五边形不可以密铺,因为它的每个内角都是108°,而360°不是108°的整数倍,在每个拼接点处的内角不能保证没有空隙或没有重叠现象。所以正五边形不可以密铺。
故答案为:C
4.D
【分析】如图所示,两个直角三角形可以拼成一个长80厘米宽40厘米的长方形。四个直角三角形可以拼成边长为80厘米的正方形。空白部分可以分成4个长80厘米宽40厘米的长方形,以及一个长80厘米的正方形。则一共需要(2×4+4)个直角三角形。
【详解】2×4+4
=8+4
=12(块)
空白部分还需要12块这样的瓷砖。
故答案为:D
5.C
【分析】一口锅一次可煎两张饼,饼有两面,煎完一面要2分钟,第一次放第1张的第一面和第2张的第一面,第二次放第1张的第二面和第3张的第一面,第三次放第2张的第二面和第3张的第二面,一共要花3个2分钟,据此计算。
【详解】3×2=6(分钟)
煎完3张饼至少需要6分钟。
故答案选:C
6.(1) 72 36 72 36
(2) 48 24 24 48
【分析】(1)用第一组图案中的,则每个小正方形的上半部分都需要一块,求出有多少个小正方形,即有多少个,进而即可得到面积; 用第一组图案中的,则每个小正方形的上半部分都需要一块,求出有多少个小正方形,即有多少个,进而即可得到面积。
(2)用第二组图案中的,则每3厘米用两个,据此即可求出有多少块,进而求得面积;用第二组图案中的,则每3厘米用一个,据此即可求出有多少块,进而求得面积。
【详解】(1)若用第1组图案,用了12×6=72块,所占面积是72÷2=36平方厘米,用了72块,所占面积是36平方厘米。
(2)若用第2组图案,用了8×6=48块,所占面积是48÷2=24平方厘米,用了4×6=24块,所占面积是24×2=48平方厘米。
7.是
【分析】平面图形密铺的特点:(1)用一种或几种全等图形进行拼接;(2)拼接处不留缝隙,不重叠;(3)连续铺成一片;据此判断。
【详解】此图即不留缝隙,也不重叠的铺满,所以这幅图是密铺。
【点睛】
8. 不是 空隙 重叠
【分析】
用一种或几种全等图形(规则图形或不规则图形)进行拼接,图形之间没有空隙,也不重复,这种铺法在数学上叫图形的密铺,也叫图形的镶嵌。图形之间没有空隙,也不重叠,是密铺。据此解答。
【详解】观察图形,平行四边形之间确实没留空隙,但是相互之间有重叠,所以不是密铺。故这幅图不是密铺,因为彼此之间不留空隙,但是重叠。
9.45
【分析】先买菜(20分钟),然后在煮饭25分钟内,可以同步完成洗菜(6分钟)+洗餐具(3分钟)+炒菜(8分钟)+摆餐具(1分钟),这样做完午餐至少需要的时间是买菜加上煮饭的时间;据此解答。
【详解】20+25=45(分钟)
即妈妈准备午餐,需要做的事情是:买菜(20分)、洗菜(6分)、洗餐具(3分)、煮饭(25分)、炒菜(8分)、摆餐具(1分).妈妈做完午餐至少需要45分钟。
10. ③ ④ ② ①
【分析】观察图形可知,第一幅图是从正面拍摄的 ,第二幅图是从右面拍摄的,第三幅图是从正面拍摄的,比第一幅图从正面拍摄的位置稍近一些,第四幅图是从左面拍摄的,据此结合图片中的位置进行判断即可。
【详解】第一幅图在③号位置拍摄,第二幅图在④号位置拍摄,第三幅图在②号位置拍摄,第四幅图在①号位置拍摄。
11.见详解
9
【分析】要使需要的时间最短,应先洗锅,然后烧热锅,在烧热锅的同时,可进行敲蛋和搅蛋。然后烧热油,在烧热油的同时,可进行切西红柿,最后炒菜。一共需要(2+2+2+3)分钟。
【详解】2+2+2+3=9(分钟)
炒好这道菜至少需要9分钟。
【点睛】本题考查优化问题,要想时间最短,应合理安排各项任务之间的顺序,注意同时进行的两项任务应互不干扰。
12.√
【分析】用形状、大小完全相同的图形进行拼接,如果能没有空隙、又不重叠地铺在同一个平面上,这种铺法就叫作“密铺”。能够密铺的图形特征是内角之和是360°。
【详解】四条边相等的平行四边形的两个锐角和两个钝角加起来恰好是360°,所以能密铺。
故答案为:√
【点睛】本题考查了密铺,掌握密铺的前提条件是解题的关键。
13.×
【分析】烧开水的同时,可以洗脸或者刷牙,需要(2+3)分钟 。
【详解】2+3=5(分)
故答案为:×
【点睛】此题属于合理安排时间问题,要本着既节约时间又不使每道工序相矛盾进行解答。
14.√
【分析】因为用自动洗衣机洗衣服可以腾出手完成擦地板的工作,所以张菊在家可以一边擦地板,一边用自动洗衣机洗衣服。
【详解】根据分析可知:
张菊在家一边擦地板,一边用自动洗衣机洗衣服,原题说法正确。
故答案为:√
【点睛】此题属于合理安排时间问题,要本着既节约时间又不使每道工序相矛盾进行解答。
15.×
【分析】平面图形密铺的特点:(1)用一种或几种全等图形进行拼接;(2)拼接处不留空隙、不重叠;(3)连续铺成一片。根据正多边形的组合能否密铺,关键是看位于同一顶点处的几个角之和能否为360°,如果能组成360°就能够密铺,反之不能。
【详解】反例:
正五边形每个内角是180°-360°÷5
=180°-72°
=108°
108°不能整除360°,不能密铺,所以任意正多边形一定都能密铺的说法错误。
故答案为:×
【点睛】本题考查平面图形的密铺。根据密铺的意义,掌握常见的密铺图形和不能密铺的图形种类是解题的关键。
16.4分钟
【分析】
王老师先通知一位同学,再和这位同学一起各再通知一位同学,所有接到通知的同学和王老师继续同时去通知其他同学,据此分析。
【详解】
第1分钟:1名
第2分钟:1+2=3(名)
第3分钟:3+4=7(名)
第4分钟:7+8=15(名)
答:最少需要4分钟。
17.见详解
【分析】
在速滑比赛中滑行的长度相同时,用的时间越少,则表示越靠前,比较三人滑行时间即可确定冠军、亚军和季军。
【详解】
34秒49>34秒39>34秒32
答:冠军是高亭宇,亚军是车旼奎,季军是森重航。
18.(1)买7张团体票和3张儿童票合算,花1650元钱;(2)买7张团体票和3张儿童票合算,花1650元钱
【分析】(1)①可以买6张成人票和4张儿童票。因为儿童票的单价小于团体票的单价,所以儿童应尽量买儿童票,那么还可以买7张团体票和3张儿童票。分别算出每种购买方式的总价,然后对它们的总价进行比较,花费最少的就是最合算的。
(2)可以买4张成人票和6张儿童票,或买7张团体票和3张儿童票。分别算出每种购买方式的总价,然后对它们的总价进行比较,花费最少的就是最合算的。
【详解】(1)购买方式一:6张成人票和4张儿童票
6×240+4×130
=1440+520
=1960(元)
购买方式二:7张团体票和3张儿童票
7×180+3×130
=1260+390
=1650(元)
1960>1650
答:买7张团体票和3张儿童票合算,花1650元钱。
(2)购买方式一:4张成人票和6张儿童票
4×240+6×130
=960+780
=1740(元)
购买方式二:7张团体票和3张儿童票
7×180+3×130
=1260+390
=1650(元)
1740>1650
答:买7张团体票和3张儿童票合算,花1650元钱。
19.见详解
【分析】先求出师生的总人数,把352与18相加,得总人数是370人。
方案一:全部租大车,计算出需要几辆大车,用总人数除以60,因为有余数,所以给商加1即为需要租车的数量,7乘60求出可以乘坐的总人数,再用车的数量乘1200即可求出总费用。
方案二:减少大车的数量,大车租6辆,其余的人租小车坐,6辆大车可以坐360人,其余的人坐小车,6乘60,所得积加36即可求出可以乘坐的总人数,再用1200乘6,所得积加800可以求出需要的总费用。
方案三:在方案二的基础上,减少大车的数量1辆,小船需要1辆,按照同样的计算方法求出总的费用,以及可以乘坐的总人数;
方案四:在方案三的基础上大车减少1辆,计算出大车可以乘坐的总人数,再用370减这个总人数,即可求出剩下的人数,再用这个人数除以36,若有余数,给商加1即为需要租小车的数量,给60乘大车数量,给36乘小车数量,再把两个积相加,即可求出可以乘坐的总人数,给大车数量乘1200,给小车数量乘800,最后相加即可求出需要租车的总费用;
方案五:在方案四的基础上大车减少1辆,计算出大车可以乘坐的总人数,用370减这个数可以求出剩下多少人,再用这个人数除以36,若有余数,给商加1即为需要租小车的数量,给60乘大车数量,给36乘小车数量,再把两个积相加,即可求出可以乘坐的总人数,给大车数量乘1200,给小车数量乘800,最后相加即可求出需要租车的总费用;
方案六:在方案五的基础上大车减少1辆,计算出大车可以乘坐的总人数,用370减这个数可以求出剩下多少人,再用这个人数除以36,若有余数,给商加1即为需要租小车的数量,给60乘大车数量,给36乘小车数量,再把两个积相加,即可求出可以乘坐的总人数,给大车数量乘1200,给小车数量乘800,最后相加即可求出需要租车的总费用;
方案七:在方案六的基础上大车减少1辆,计算出大车可以乘坐的总人数,用370减这个数可以求出剩下多少人,再用这个人数除以36,若有余数,给商加1即为需要租小车的数量,给60乘大车数量,给36乘小车数量,再把两个积相加,即可求出可以乘坐的总人数,给大车数量乘1200,给小车数量乘800,最后相加即可求出需要租车的总费用;
方案八:全部租小车,用总人数370除以36求出要租几辆小车还剩几人,再用商加1求需要租小车的数量,要求可以乘坐多少人,给小车的数量乘36即可,求费用把小车的数量与800相乘即可。
【详解】352+18=370(人)
方案一:全部租大车,370÷60=6(辆)……10(人)
6+1=7(辆)
1200×7=8400(元)
方案二:7-1=6(辆)
370-60×6
=370-360
=10(人)
6×60+36
=360+36
=396(人)
1200×6+800
=7200+800
=8000(元)
方案三:6-1=5(辆)
370-60×5
=370-300
=70(人)
70÷36=1(辆)……34(人)
1+1=2(辆)
36×2+60×5
=72+300
=372(人)
800×2+1200×5
=1600+6000
=7600(元)
方案四:5-1=4(辆)
370-60×4
=370-240
=130(人)
130÷36=3(辆)……22(人)
3+1=4(辆)
36×4+60×4
=144+240
=384(人)
800×4+1200×4
=3200+4800
=8000(元)
方案五:4-1=3(辆)
370-60×3
=370-180
=190(人)
190÷36=5(辆)……10(人)
5+1=6(辆)
36×6+60×3
=216+180
=396(人)
800×6+1200×3
=4800+3600
=8400(元)
方案六:3-1=2(辆)
370-60×2
=370-120
=250(人)
250÷36=6(辆)……34(人)
6+1=7(辆)
36×7+60×2
=252+120
=372(人)
800×7+1200×2
=5600+2400
=8000(元)
方案七:2-1=1(辆)
370-60=310(人)
310÷36=8(辆)……22(人)
8+1=9(辆)
36×9+60
=324+60
=384(人)
800×9+1200
=7200+1200
=8400(元)
方案八:370÷36=10(辆)……10(人)
10+1=11(辆)
11×36=396(人)
11×800=8800(元)
方案 大车/辆 小车/辆 可坐人数/人 总费用/元
方案一 7 0 420 8400
方案二 6 1 396 8000
方案三 5 2 372 7600
方案四 4 4 384 8000
方案五 3 6 396 8400
方案六 2 7 372 8000
方案七 1 9 384 8400
方案八 0 11 396 8800
答:租5辆大车和2辆小车最划算。
【点睛】根据1辆车可以乘坐的人数×车的数量,来求可以乘坐的总人数,根据租1辆车的费用×车的数量来求租车的费用。
20.一共租7辆大卡车和3辆小卡车运费最低,总运费为1670元
【分析】先算出大卡车运输每吨货物的运费为:200÷10=20(元),小卡车运输每吨货物的运费为:90÷4=22.5(元),因为22.5>20,所以选择尽可能多的大卡车并且车能得到完全利用,更划算点;第一种方案:租用大卡车8辆,小卡车1辆,总运费为:200×8+90=1690(元);第二种方案为:租用大卡车7辆,小卡车3辆,总运费为:200×7+90×3=1670(元);第三种方案为:租用大卡车6辆,小卡车6辆,总运费为:200×6+90×6=1740(元);因为1670<1690<1740,所以一共租7辆大卡车和3辆小卡车运费最低,总运费为1670元。
【详解】由分析可知:
租用大卡车7辆,小卡车3辆
总运费为:200×7+90×3
=1400+270
=1670(元)
答:一共租7辆大卡车和3辆小卡车运费最低,总运费为1670元。
【点睛】本题考查优化问题,需先算出大卡车和小卡车每吨的运费,看尽量多用哪种车运输更划算,还要考虑车是否得到完全利用。
21.(1)A、C、D;
(2)见详解
【分析】(1)用一种或几种全等图形(规则图形或不规则图形)进行拼接,图形之间没有空隙,也不重复,这种铺法在数学上叫图形的密铺,也叫图形的镶嵌。任何弧线图形不能密铺;除正三角形、正四边形和正六边形外,其他正多边形都不可以密铺平面;所有任意三角形与任意四边形都可以密铺。
(2)观察地砖的形状,先铺一铺,看平铺时砖块之间是否有空隙或砖块是否重叠,把密铺后的图形画在方框里即可。
【详解】(1)能够进行密铺的地砖形状是(A、C、D)。
(2)如图:
【点睛】本题考查平面图形的密铺。根据密铺的意义,掌握常见的密铺图形和不能密铺的图形种类是解题的关键。
22.画图见详解
<;>
【分析】直线上一大格表示0.1,一小格表示0.01,据此表示出0.24,0.31,0.5,0.05。小数比较大小时,先看它们的整数部分,整数部分大的那个数就大;如果整数部分相同,十分位上的数大的那个数就大;如果十分位上的数相同,百分位上的数大的那个数就大……
【详解】
0.24<0.31 0.5>0.05
【点睛】本题考查小数的意义以及小数比较大小的方法,小数比较大小的方法与整数基本相同,都是从高位起,依次把相同数位上的数进行比较。
23.(1)10;10;15;20;25
(2)见详解
【分析】若贴1个玩具,需要2个5分钟,即(2×5)分钟。若贴2个玩具,也需要2个5分钟,即(2×5)分钟。若贴3个玩具,假设这3个玩具分别为a、b、c;第一次贴a、b的正面;第二次贴a的反面和c的正面;第三次贴b、c的反面。所以贴3个玩具需要(3×5)分钟。若贴4个玩具,可以分成2组,每组2个玩具,需要(2×2×5)分钟。若贴5个玩具,可以分成2组,一组2个玩具,一组3个玩具,需要(2×5+3×5)分钟。
【详解】(1)2×5=10(分钟)
3×5=15(分钟)
4÷2×10
=2×10
=20(分钟)
2×5+3×5
=10+15
=25(分钟)
贴玩具的个数 1 2 3 4 5
最少需要的时间/分 10 10 15 20 25
(2)当贴玩具的个数大于或等于2个时,贴玩具的个数×贴一面的时间=最少需要的时间。
【点睛】在优化问题中,要统筹安排贴图案的顺序,使机器里始终没有空位,这样才能保证需要的时间最短。
答案第1页,共2页
答案第1页,共2页
