【北师大版九上同步练习】 第一章 特殊平行四边形(培优)检测题(含答案)
文档属性
| 名称 | 【北师大版九上同步练习】 第一章 特殊平行四边形(培优)检测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 12.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-10 16:45:39 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【北师大版九上同步练习】
第一章特殊平行四边形(培优)检测题
一、单选题
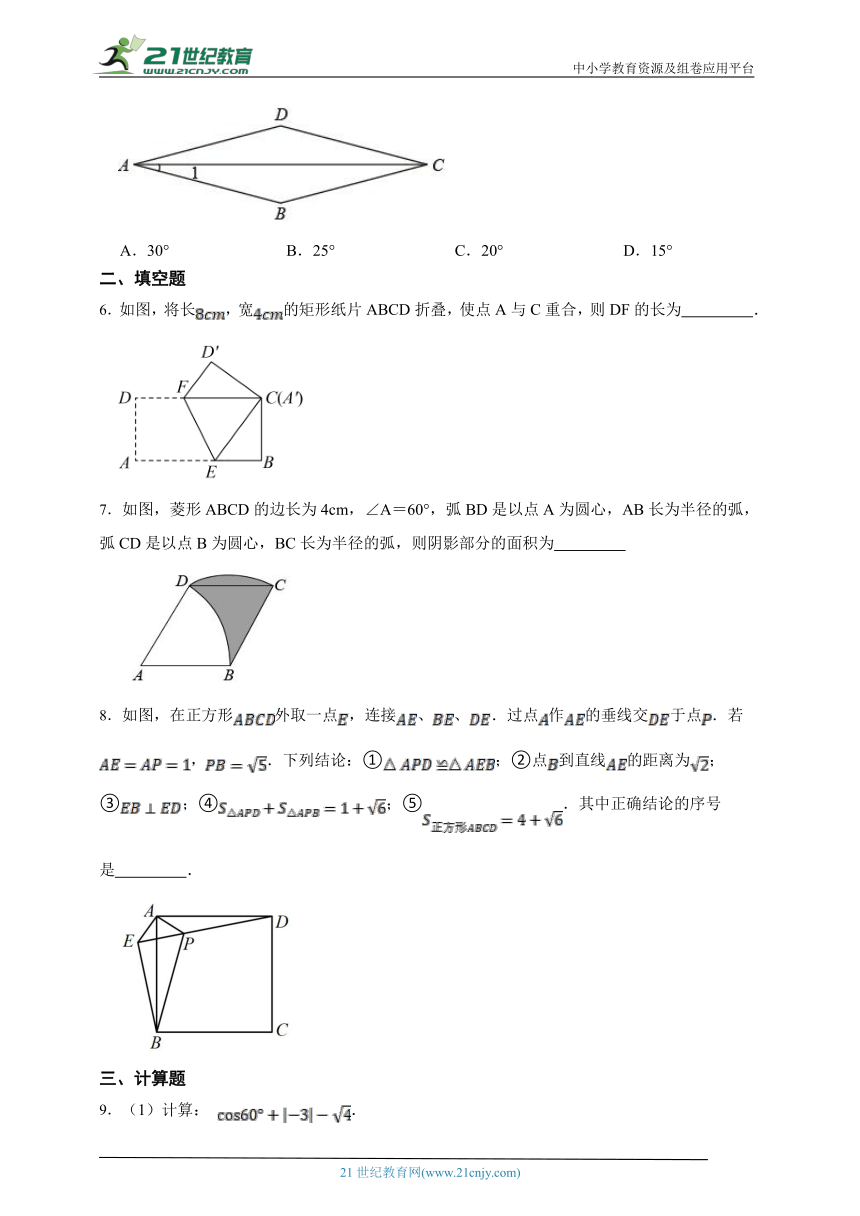
1.如图,在中,,则( )
A. B. C. D.
2.如图,中,,,,以点为圆心,长为半径作圆弧交于点,则长在( )
A.0与1之间 B.1与2之间 C.2与3之间 D.3与4之间
3.下列性质中正方形具有而矩形没有的( )
A.对角线互相平分 B.对角线相等
C.对角线互相垂直 D.四个角都是直角
4.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,点E为垂足,连接DF,则∠CDF为( )
A.80° B.70° C.65° D.60°
5.如图,菱形ABCD中, ,则 ( )
A.30° B.25° C.20° D.15°
二、填空题
6.如图,将长,宽的矩形纸片ABCD折叠,使点A与C重合,则DF的长为 .
7.如图,菱形ABCD的边长为4cm,∠A=60°,弧BD是以点A为圆心,AB长为半径的弧,弧CD是以点B为圆心,BC长为半径的弧,则阴影部分的面积为
8.如图,在正方形外取一点,连接、、.过点作的垂线交于点.若,.下列结论:①;②点到直线的距离为;③;④;⑤.其中正确结论的序号是 .
三、计算题
9.(1)计算: .
(2)解分式方程:.
四、解答题
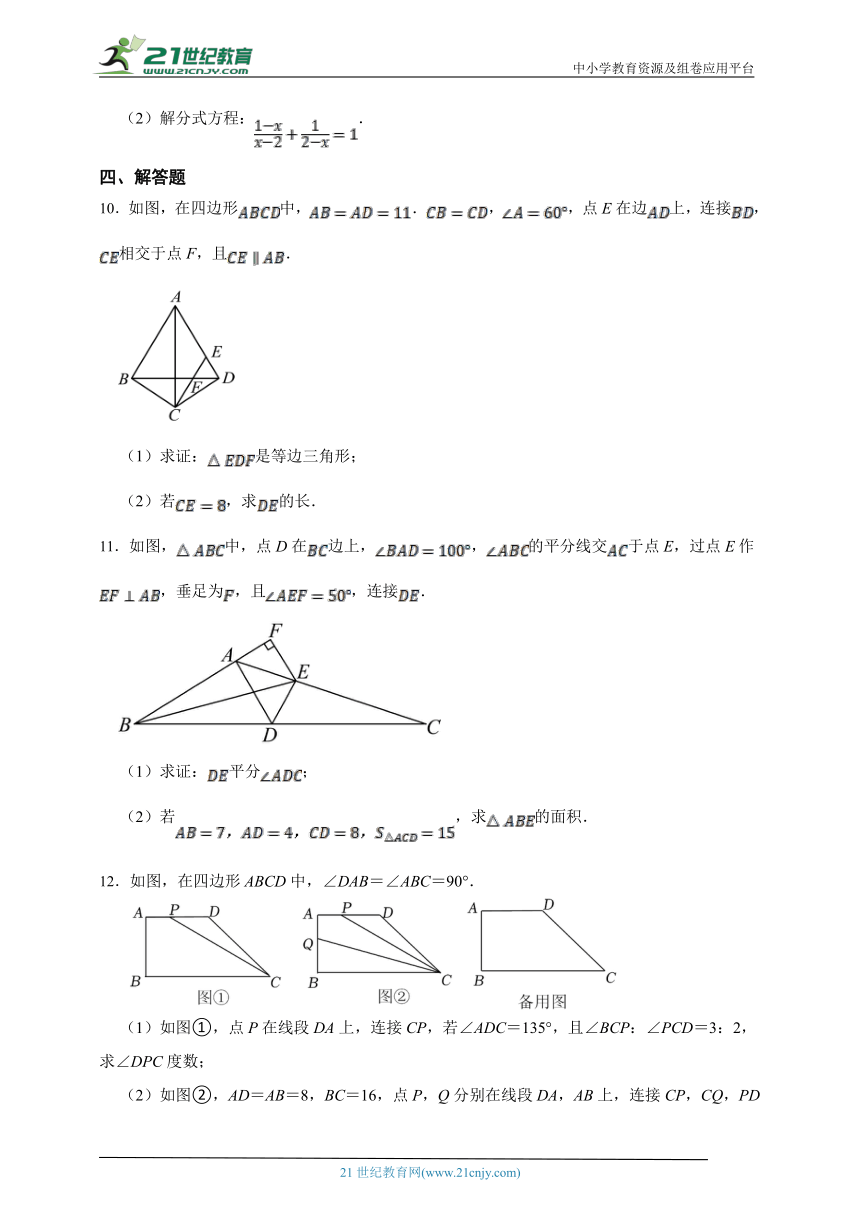
10.如图,在四边形中,.,,点E在边上,连接,相交于点F,且.
(1)求证:是等边三角形;
(2)若,求的长.
11.如图,中,点D在边上,,的平分线交于点E,过点E作,垂足为,且,连接.
(1)求证:平分;
(2)若,求的面积.
12.如图,在四边形ABCD中,∠DAB=∠ABC=90°.
(1)如图①,点P在线段DA上,连接CP,若∠ADC=135°,且∠BCP:∠PCD=3:2,求∠DPC度数;
(2)如图②,AD=AB=8,BC=16,点P,Q分别在线段DA,AB上,连接CP,CQ,PD=2AQ且满足S△DCP=S四边形APCQ,求AQ的长;
(3)点P,Q分别在线段DA,AB的延长线上,点M在线段BQ上,∠QPM=k∠APQ,∠QCM=k∠BCM,且∠APQ+∠BCM=100°,∠PMC﹣∠PQC=40°,请补全图形并求出k的值.
五、综合题
13.如图, 和 中, , , ,AB,DE相交于点F,AD,BC相交于点G.
(1)求证: ;
(2)若 , ,求DG的长.
14.如图, ABCD中,E为BC边的中点,连接AE并延长交DC的延长线于点F,延长EC至点G,使CG=CE,连接DG、DE、FG.
(1)求证:△ABE≌△FCE;
(2)若AD=2AB,求证:四边形DEFG是矩形.
15.如图,在平面直角坐标系中,O是坐标原点,长方形OABC的顶点A,C分别在x轴和y轴的正半轴上.已知,,点P从点C出发沿线段的方向运动,当点P与点A重合时停止运动.
(1)请写出点B的坐标,
(2)当点P到x轴和y轴的距离相等时,求点P的坐标;
(3)设点B关于x轴对称的点为,求点到直线CA的距离;
(4)已知,点P在运动过程中是否存在为等腰三角形的情况 若存在,请直接写出点P的坐标;若不存在,请说明理由.
六、实践探究题
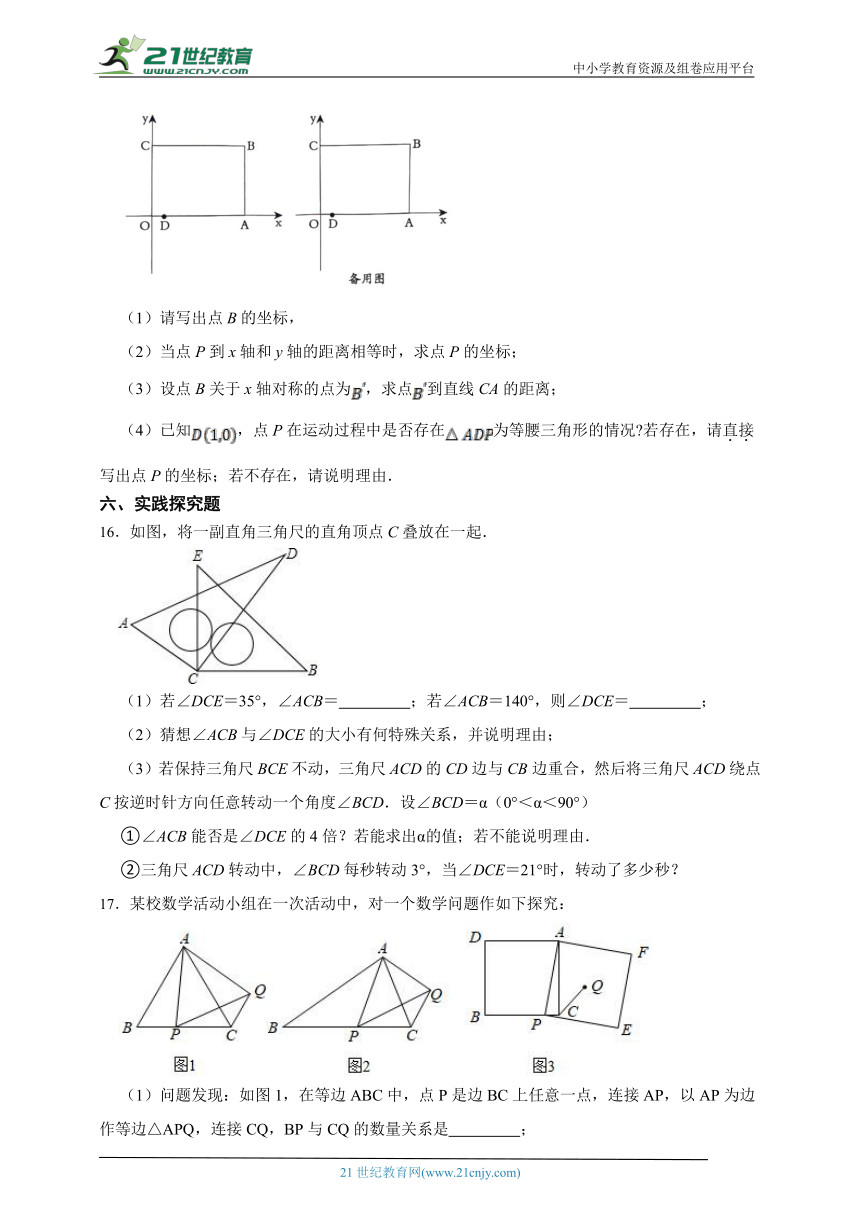
16.如图,将一副直角三角尺的直角顶点C叠放在一起.
(1)若∠DCE=35°,∠ACB= ;若∠ACB=140°,则∠DCE= ;
(2)猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(3)若保持三角尺BCE不动,三角尺ACD的CD边与CB边重合,然后将三角尺ACD绕点C按逆时针方向任意转动一个角度∠BCD.设∠BCD=α(0°<α<90°)
①∠ACB能否是∠DCE的4倍?若能求出α的值;若不能说明理由.
②三角尺ACD转动中,∠BCD每秒转动3°,当∠DCE=21°时,转动了多少秒?
17.某校数学活动小组在一次活动中,对一个数学问题作如下探究:
(1)问题发现:如图1,在等边ABC中,点P是边BC上任意一点,连接AP,以AP为边作等边△APQ,连接CQ,BP与CQ的数量关系是 ;
(2)变式探究:如图2,在等腰△ABC中,AB=BC,点P是边BC上任意一点,以AP为腰作等腰△APQ,使AP=PQ,∠APQ=∠ABC,连接CQ,判断∠ABC和∠ACQ的数量关系,并说明理由;
(3)解决问题:如图3,在正方形ADBC中,点P是边BC上一点,以AP为边作正方形APEF,Q是正方形APEF的中心,连接CQ.若正方形APEF的边长为5,CQ=,求正方形ADBC的边长.
18.【问题背景】光线照射到镜面会产生反射现象,小圳在做镜面反射实验时发现:当光线经过镜面反射时,入射光线、反射光线与镜面所夹的角对应相等.例如:在图1中,有.
(1)【初步探究】如图2,设镜子AB与BC的夹角,当 时,小圳发现入射光线EF与反射光线GH恰好平行.
(2)【深入探究】如图3,小圳渐渐改变两镜面之间夹角,使得是一个锐角,从F点发出一条光线EF经过2次反射又回到了点F,入射光线EF与第2次反射光线GF的夹角为.用含的式子表示.
(3)【拓展应用】如图4,小圳继续改变两镜面之间夹角,使得,若也是一个钝角,入射光线EF与镜面AB的夹角.已知入射光线EF从镜面AB开始反射,经过3次反射,当第3次反射光线与入射光线EF平行时,求出的度数.
答案解析部分
1.【答案】A
【知识点】平行四边形的性质
2.【答案】B
【知识点】无理数的估值;勾股定理
3.【答案】C
【知识点】矩形的性质;正方形的性质
4.【答案】D
【知识点】菱形的性质
5.【答案】D
【知识点】菱形的性质
6.【答案】3
【知识点】勾股定理;矩形的性质;翻折变换(折叠问题)
7.【答案】cm2
【知识点】菱形的性质;扇形面积的计算
8.【答案】①③⑤
【知识点】勾股定理;正方形的性质;几何图形的面积计算-割补法;三角形全等的判定(SAS)
9.【答案】(1);(2)
【知识点】解分式方程;特殊角的三角函数值
10.【答案】(1)证明:,,
是等边三角形,
,
,
,,
,
是等边三角形;
(2)解:,
在和中,
,
,
.
,
,
,
.
,
,
.
【知识点】平行线的性质;三角形全等及其性质;等边三角形的判定与性质;三角形全等的判定(SSS)
11.【答案】(1)证明:如图,过点E作于G,于H,
∵,
∴,
∵,
∴,
∴,
∴为的平分线,
又,
∴,
∵是的平分线,
∴,
∴,
∴点E在的平分线上,
∴平分;
(2)解:设,则,
∴,即:,
解得,,
∴,
∴的面积为.
【知识点】三角形的面积;三角形内角和定理;角平分线的性质
12.【答案】(1)解:∵∠DAB=∠ABC=90°,
∴∠ABC+∠ABC=180°,
∴AD∥CB,
∴∠DCB=180°﹣135°=45°,
∵∠BCP:∠PCD=3:2,
∴∠PCD=∠DCB=18°,
∴∠DPC=180°﹣135°﹣18°=27°;
(2)解:设AQ=x,则BQ=8﹣x,PD=2x,
∵S△DCP=S四边形APCQ,
∴×2x×8=×[×(8+16)×8﹣×16×(8﹣x)﹣×2x×8],
解得x=2,
∴AQ=2;
(3)解:如图③中,设∠APQ=x,∠BCM=y,则∠QPM=kx,∠QCM=ky,
∵∠APQ+∠BCM=100°,
∴x+y=100°,
∵∠CMP+∠MPQ=∠PQC+∠MCQ,
∴∠CMP﹣∠PQC=∠MCQ+∠MPQ=ky+kx=40°,
∴k=.
【知识点】平行线的判定与性质;三角形的面积;三角形内角和定理;三角形的外角性质
13.【答案】(1)证明: ,
,即 .
又 , ,
(ASA).
(2)解: , .
, .
又 , .
【知识点】全等三角形的判定与性质
14.【答案】(1)证明:∵四边形ABCD是平行四边形,再证明DF=EG,即可证明四边形DEFG是矩形.
∴ABCD,
∴∠EAB=∠CFE,
又∵E为BC的中点,
∴EC=EB,
∴在△ABE和△FCE中,
,
∴△ABE≌△FCE(AAS);
(2)证明:∵△ABE≌△FCE,
∴AB=CF,
∵四边形ABCD是平行四边形,
∴AB=DC,
∴DC=CF,
又∵CE=CG,
∴四边形DEFG是平行四边形,
∵E为BC的中点,CE=CG,
∴BC=EG,
又∵AD=BC=EG=2AB,DF=CD+CF=2CD=2AB,
∴DF=EG,
∴平行四边形DEFG是矩形.
【知识点】平行线的性质;平行四边形的判定与性质;矩形的判定;三角形全等的判定(AAS)
15.【答案】(1)解:点B的坐标是
(2)解:如图1,当点P到x轴和y轴的距离相等时,点P在边CB上,且OP平分,
即,,,
∴点P的坐标为
(3)解:由题意得点的坐标为,∴.
如图1,过点作,交CA的延长线于点E.
∵,,∴.
在中,∵,∴,
即点到直线CA的距离为4.8
(4)解:存在,点P的坐标为或或.
∵,∴,∴.
①当时,点P在边CB上,如图2,
∵,∴,∴;
②当时,点P在DA的垂直平分线上,此时;
③当时,点P在边CB上,如图3,
过点P作于点F,则,∴,
∴,∴
【知识点】点的坐标;三角形的面积;勾股定理;角平分线的定义;四边形-动点问题
16.【答案】(1)145°;40°
(2)解:∠ACB+∠DCE=180°或互补,
理由:∵∠ACE+∠ECD+∠DCB+∠ECD=180.
∵∠ACE+∠ECD+∠DCB=∠ACB,
∴∠ACB+∠DCE=180°,即∠ACB与∠DCE互补.
(3)解:①当∠ACB是∠DCE的4倍,
∴设∠ACB=4x,∠DCE=x,
∵∠ACB+∠DCE=180°,
∴4x+x=180°
解得:x=36°,
∴α=90°﹣36°=54°;
②设当∠DCE=21°时,转动了t秒,
∵∠BCD+∠DCE=90°,
∴3t+21=90,
t=23°,
答:当∠DCE=21°时,转动了23秒.
【知识点】角的运算;余角、补角及其性质;一元一次方程的实际应用-几何问题
17.【答案】(1)BP=CQ
(2)解:变式探究:∠ABC=∠ACQ,
理由如下:∵AB=BC,
∴∠BAC=,
∵AP=PQ,
∴∠PAQ=,
∵∠APQ=∠ABC,
∴∠BAC=∠PAQ,
∴△BAC∽△PAQ,
∴
∵∠BAP+∠PAC=∠PAC+∠CAQ,
∴∠BAP=∠CAQ,
∴△BAP∽△CAQ,
∴∠ABC=∠ACQ;
(3)解:解决问题:如图3,连接AB、AQ,
∵四边形ADBC是正方形,
∴=,∠BAC=45°,
∵Q是正方形APEF的中心,
∴=,∠PAQ=45°,
∴∠BAP+∠PAC=∠PAC+∠CAQ,即∠BAP=∠CAQ,
∵=,
∴△ABP∽△ACQ,
∴==,
∵CQ=,
∴BP=1,
设PC=x,则 BC=AC=1+x,
在Rt△APC中,AP2=AC2+PC2,即52=(1+x)2+x2,
解得,x1=﹣4(舍去),x2=3,
∴正方形ADBC的边长为:3+1=4.
【知识点】等边三角形的性质;勾股定理;正方形的性质;相似三角形的判定与性质;三角形全等的判定(SAS)
18.【答案】(1)90°
(2)解:如图3,∵∠1=∠2,∠3=∠4,∠3+∠2=180°-,
∴∠1+∠4=180°-,
∵∠1+∠2+∠FEG+∠3+∠4+∠EGH=360°,
∴∠FEG+∠EGF=2,
∵∠FEG+∠EGF+∠EFG=180°,
∴∠EFG=180°-;
(3)解:如图4,过点G作GM∥EF,
∵∠BEG=∠1=30°, ,
∴∠BGE=∠CGH=180°-110°-30°=40°,∠FEG=180°-2∠1=120°,
∴∠EGH=180°-2∠BGE=100°,
∵EF∥GM,EF∥HK,
∴GM∥HK,
∴∠FEG+∠EGM=∠MGH+∠KHG=180°,
∴∠FEG+∠EGH+∠GHK=360°,
∴∠GHK=360°-120°-100°=140°,
∴∠GHC=20°,
∵∠BCD+∠CGH+∠GHC=180°,
∴∠BCD=180°-40°-20°=120°.
【知识点】平行线的判定与性质;三角形内角和定理
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【北师大版九上同步练习】
第一章特殊平行四边形(培优)检测题
一、单选题
1.如图,在中,,则( )
A. B. C. D.
2.如图,中,,,,以点为圆心,长为半径作圆弧交于点,则长在( )
A.0与1之间 B.1与2之间 C.2与3之间 D.3与4之间
3.下列性质中正方形具有而矩形没有的( )
A.对角线互相平分 B.对角线相等
C.对角线互相垂直 D.四个角都是直角
4.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,点E为垂足,连接DF,则∠CDF为( )
A.80° B.70° C.65° D.60°
5.如图,菱形ABCD中, ,则 ( )
A.30° B.25° C.20° D.15°
二、填空题
6.如图,将长,宽的矩形纸片ABCD折叠,使点A与C重合,则DF的长为 .
7.如图,菱形ABCD的边长为4cm,∠A=60°,弧BD是以点A为圆心,AB长为半径的弧,弧CD是以点B为圆心,BC长为半径的弧,则阴影部分的面积为
8.如图,在正方形外取一点,连接、、.过点作的垂线交于点.若,.下列结论:①;②点到直线的距离为;③;④;⑤.其中正确结论的序号是 .
三、计算题
9.(1)计算: .
(2)解分式方程:.
四、解答题
10.如图,在四边形中,.,,点E在边上,连接,相交于点F,且.
(1)求证:是等边三角形;
(2)若,求的长.
11.如图,中,点D在边上,,的平分线交于点E,过点E作,垂足为,且,连接.
(1)求证:平分;
(2)若,求的面积.
12.如图,在四边形ABCD中,∠DAB=∠ABC=90°.
(1)如图①,点P在线段DA上,连接CP,若∠ADC=135°,且∠BCP:∠PCD=3:2,求∠DPC度数;
(2)如图②,AD=AB=8,BC=16,点P,Q分别在线段DA,AB上,连接CP,CQ,PD=2AQ且满足S△DCP=S四边形APCQ,求AQ的长;
(3)点P,Q分别在线段DA,AB的延长线上,点M在线段BQ上,∠QPM=k∠APQ,∠QCM=k∠BCM,且∠APQ+∠BCM=100°,∠PMC﹣∠PQC=40°,请补全图形并求出k的值.
五、综合题
13.如图, 和 中, , , ,AB,DE相交于点F,AD,BC相交于点G.
(1)求证: ;
(2)若 , ,求DG的长.
14.如图, ABCD中,E为BC边的中点,连接AE并延长交DC的延长线于点F,延长EC至点G,使CG=CE,连接DG、DE、FG.
(1)求证:△ABE≌△FCE;
(2)若AD=2AB,求证:四边形DEFG是矩形.
15.如图,在平面直角坐标系中,O是坐标原点,长方形OABC的顶点A,C分别在x轴和y轴的正半轴上.已知,,点P从点C出发沿线段的方向运动,当点P与点A重合时停止运动.
(1)请写出点B的坐标,
(2)当点P到x轴和y轴的距离相等时,求点P的坐标;
(3)设点B关于x轴对称的点为,求点到直线CA的距离;
(4)已知,点P在运动过程中是否存在为等腰三角形的情况 若存在,请直接写出点P的坐标;若不存在,请说明理由.
六、实践探究题
16.如图,将一副直角三角尺的直角顶点C叠放在一起.
(1)若∠DCE=35°,∠ACB= ;若∠ACB=140°,则∠DCE= ;
(2)猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(3)若保持三角尺BCE不动,三角尺ACD的CD边与CB边重合,然后将三角尺ACD绕点C按逆时针方向任意转动一个角度∠BCD.设∠BCD=α(0°<α<90°)
①∠ACB能否是∠DCE的4倍?若能求出α的值;若不能说明理由.
②三角尺ACD转动中,∠BCD每秒转动3°,当∠DCE=21°时,转动了多少秒?
17.某校数学活动小组在一次活动中,对一个数学问题作如下探究:
(1)问题发现:如图1,在等边ABC中,点P是边BC上任意一点,连接AP,以AP为边作等边△APQ,连接CQ,BP与CQ的数量关系是 ;
(2)变式探究:如图2,在等腰△ABC中,AB=BC,点P是边BC上任意一点,以AP为腰作等腰△APQ,使AP=PQ,∠APQ=∠ABC,连接CQ,判断∠ABC和∠ACQ的数量关系,并说明理由;
(3)解决问题:如图3,在正方形ADBC中,点P是边BC上一点,以AP为边作正方形APEF,Q是正方形APEF的中心,连接CQ.若正方形APEF的边长为5,CQ=,求正方形ADBC的边长.
18.【问题背景】光线照射到镜面会产生反射现象,小圳在做镜面反射实验时发现:当光线经过镜面反射时,入射光线、反射光线与镜面所夹的角对应相等.例如:在图1中,有.
(1)【初步探究】如图2,设镜子AB与BC的夹角,当 时,小圳发现入射光线EF与反射光线GH恰好平行.
(2)【深入探究】如图3,小圳渐渐改变两镜面之间夹角,使得是一个锐角,从F点发出一条光线EF经过2次反射又回到了点F,入射光线EF与第2次反射光线GF的夹角为.用含的式子表示.
(3)【拓展应用】如图4,小圳继续改变两镜面之间夹角,使得,若也是一个钝角,入射光线EF与镜面AB的夹角.已知入射光线EF从镜面AB开始反射,经过3次反射,当第3次反射光线与入射光线EF平行时,求出的度数.
答案解析部分
1.【答案】A
【知识点】平行四边形的性质
2.【答案】B
【知识点】无理数的估值;勾股定理
3.【答案】C
【知识点】矩形的性质;正方形的性质
4.【答案】D
【知识点】菱形的性质
5.【答案】D
【知识点】菱形的性质
6.【答案】3
【知识点】勾股定理;矩形的性质;翻折变换(折叠问题)
7.【答案】cm2
【知识点】菱形的性质;扇形面积的计算
8.【答案】①③⑤
【知识点】勾股定理;正方形的性质;几何图形的面积计算-割补法;三角形全等的判定(SAS)
9.【答案】(1);(2)
【知识点】解分式方程;特殊角的三角函数值
10.【答案】(1)证明:,,
是等边三角形,
,
,
,,
,
是等边三角形;
(2)解:,
在和中,
,
,
.
,
,
,
.
,
,
.
【知识点】平行线的性质;三角形全等及其性质;等边三角形的判定与性质;三角形全等的判定(SSS)
11.【答案】(1)证明:如图,过点E作于G,于H,
∵,
∴,
∵,
∴,
∴,
∴为的平分线,
又,
∴,
∵是的平分线,
∴,
∴,
∴点E在的平分线上,
∴平分;
(2)解:设,则,
∴,即:,
解得,,
∴,
∴的面积为.
【知识点】三角形的面积;三角形内角和定理;角平分线的性质
12.【答案】(1)解:∵∠DAB=∠ABC=90°,
∴∠ABC+∠ABC=180°,
∴AD∥CB,
∴∠DCB=180°﹣135°=45°,
∵∠BCP:∠PCD=3:2,
∴∠PCD=∠DCB=18°,
∴∠DPC=180°﹣135°﹣18°=27°;
(2)解:设AQ=x,则BQ=8﹣x,PD=2x,
∵S△DCP=S四边形APCQ,
∴×2x×8=×[×(8+16)×8﹣×16×(8﹣x)﹣×2x×8],
解得x=2,
∴AQ=2;
(3)解:如图③中,设∠APQ=x,∠BCM=y,则∠QPM=kx,∠QCM=ky,
∵∠APQ+∠BCM=100°,
∴x+y=100°,
∵∠CMP+∠MPQ=∠PQC+∠MCQ,
∴∠CMP﹣∠PQC=∠MCQ+∠MPQ=ky+kx=40°,
∴k=.
【知识点】平行线的判定与性质;三角形的面积;三角形内角和定理;三角形的外角性质
13.【答案】(1)证明: ,
,即 .
又 , ,
(ASA).
(2)解: , .
, .
又 , .
【知识点】全等三角形的判定与性质
14.【答案】(1)证明:∵四边形ABCD是平行四边形,再证明DF=EG,即可证明四边形DEFG是矩形.
∴ABCD,
∴∠EAB=∠CFE,
又∵E为BC的中点,
∴EC=EB,
∴在△ABE和△FCE中,
,
∴△ABE≌△FCE(AAS);
(2)证明:∵△ABE≌△FCE,
∴AB=CF,
∵四边形ABCD是平行四边形,
∴AB=DC,
∴DC=CF,
又∵CE=CG,
∴四边形DEFG是平行四边形,
∵E为BC的中点,CE=CG,
∴BC=EG,
又∵AD=BC=EG=2AB,DF=CD+CF=2CD=2AB,
∴DF=EG,
∴平行四边形DEFG是矩形.
【知识点】平行线的性质;平行四边形的判定与性质;矩形的判定;三角形全等的判定(AAS)
15.【答案】(1)解:点B的坐标是
(2)解:如图1,当点P到x轴和y轴的距离相等时,点P在边CB上,且OP平分,
即,,,
∴点P的坐标为
(3)解:由题意得点的坐标为,∴.
如图1,过点作,交CA的延长线于点E.
∵,,∴.
在中,∵,∴,
即点到直线CA的距离为4.8
(4)解:存在,点P的坐标为或或.
∵,∴,∴.
①当时,点P在边CB上,如图2,
∵,∴,∴;
②当时,点P在DA的垂直平分线上,此时;
③当时,点P在边CB上,如图3,
过点P作于点F,则,∴,
∴,∴
【知识点】点的坐标;三角形的面积;勾股定理;角平分线的定义;四边形-动点问题
16.【答案】(1)145°;40°
(2)解:∠ACB+∠DCE=180°或互补,
理由:∵∠ACE+∠ECD+∠DCB+∠ECD=180.
∵∠ACE+∠ECD+∠DCB=∠ACB,
∴∠ACB+∠DCE=180°,即∠ACB与∠DCE互补.
(3)解:①当∠ACB是∠DCE的4倍,
∴设∠ACB=4x,∠DCE=x,
∵∠ACB+∠DCE=180°,
∴4x+x=180°
解得:x=36°,
∴α=90°﹣36°=54°;
②设当∠DCE=21°时,转动了t秒,
∵∠BCD+∠DCE=90°,
∴3t+21=90,
t=23°,
答:当∠DCE=21°时,转动了23秒.
【知识点】角的运算;余角、补角及其性质;一元一次方程的实际应用-几何问题
17.【答案】(1)BP=CQ
(2)解:变式探究:∠ABC=∠ACQ,
理由如下:∵AB=BC,
∴∠BAC=,
∵AP=PQ,
∴∠PAQ=,
∵∠APQ=∠ABC,
∴∠BAC=∠PAQ,
∴△BAC∽△PAQ,
∴
∵∠BAP+∠PAC=∠PAC+∠CAQ,
∴∠BAP=∠CAQ,
∴△BAP∽△CAQ,
∴∠ABC=∠ACQ;
(3)解:解决问题:如图3,连接AB、AQ,
∵四边形ADBC是正方形,
∴=,∠BAC=45°,
∵Q是正方形APEF的中心,
∴=,∠PAQ=45°,
∴∠BAP+∠PAC=∠PAC+∠CAQ,即∠BAP=∠CAQ,
∵=,
∴△ABP∽△ACQ,
∴==,
∵CQ=,
∴BP=1,
设PC=x,则 BC=AC=1+x,
在Rt△APC中,AP2=AC2+PC2,即52=(1+x)2+x2,
解得,x1=﹣4(舍去),x2=3,
∴正方形ADBC的边长为:3+1=4.
【知识点】等边三角形的性质;勾股定理;正方形的性质;相似三角形的判定与性质;三角形全等的判定(SAS)
18.【答案】(1)90°
(2)解:如图3,∵∠1=∠2,∠3=∠4,∠3+∠2=180°-,
∴∠1+∠4=180°-,
∵∠1+∠2+∠FEG+∠3+∠4+∠EGH=360°,
∴∠FEG+∠EGF=2,
∵∠FEG+∠EGF+∠EFG=180°,
∴∠EFG=180°-;
(3)解:如图4,过点G作GM∥EF,
∵∠BEG=∠1=30°, ,
∴∠BGE=∠CGH=180°-110°-30°=40°,∠FEG=180°-2∠1=120°,
∴∠EGH=180°-2∠BGE=100°,
∵EF∥GM,EF∥HK,
∴GM∥HK,
∴∠FEG+∠EGM=∠MGH+∠KHG=180°,
∴∠FEG+∠EGH+∠GHK=360°,
∴∠GHK=360°-120°-100°=140°,
∴∠GHC=20°,
∵∠BCD+∠CGH+∠GHC=180°,
∴∠BCD=180°-40°-20°=120°.
【知识点】平行线的判定与性质;三角形内角和定理
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
