【北师大版九上同步练习】 2.1 认识一元二次方程(含答案)
文档属性
| 名称 | 【北师大版九上同步练习】 2.1 认识一元二次方程(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-10 16:32:30 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【北师大版九上同步练习】 2.1认识一元二次方程
一、单选题
1.一元二次方程的一次项系数是( )
A. B.-2 C.-7 D.2
2.若方程化为一元二次方程的一般形式后不含一次项,则的值为( )
A.0 B. C.3 D.
3.若关于的方程是一元二次方程,则的值是( )
A.-1 B.2 C.-1或3 D.3
4.《九章算术》是中国传统数学最重要的著作,书中有一个关于门和竹竿的问题,简译为:今有一扇门,不知门的高和宽.另有一竹竿,也不知竹竿的长短.竹竿横着放时比门的宽长4尺,竹竿竖着放时比门的高长2尺,竹竿斜着放时与门的对角线恰好相等,求门的对角线长.若设门的对角线长为尺,则可列方程为( )
A. B.
C. D.
5.下列各式中是一元二次方程的是( )
A.x2+x=2y B.x2=1 C.ax2+bx+c=0 D.x2﹣2=x2+1
二、填空题
6.将化成一元二次方程的一般形式的结果为+ =0.
7.若关于x的方程是一元二次方程,则m的值为
8.关于x的方程(1-m2)x2+2mx-1=0的所有根都是比1小的正实数,则实数m的取值范围是 .
三、计算题
9.若(m+1) +6-2=0是关于x的一元二次方程,求m的值.
10.已知分式 ,若n满足一元二次方程n2+n-2=0,先化简原分式,再求值。
四、解答题
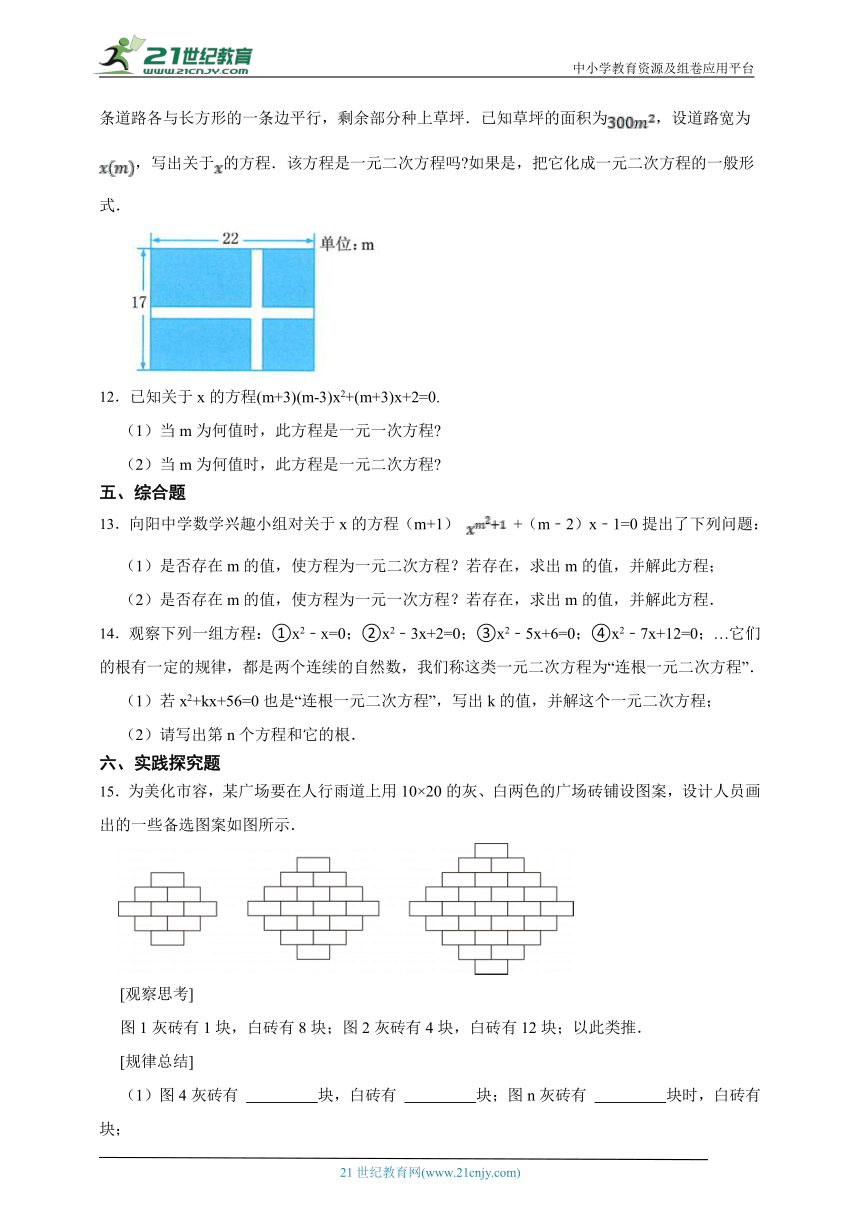
11.如图,在一块长为,宽为的长方形地面上,要修建同样宽的两条互相垂直的道路.两条道路各与长方形的一条边平行,剩余部分种上草坪.已知草坪的面积为,设道路宽为,写出关于的方程.该方程是一元二次方程吗 如果是,把它化成一元二次方程的一般形式.
12.已知关于x的方程(m+3)(m-3)x2+(m+3)x+2=0.
(1)当m为何值时,此方程是一元一次方程
(2)当m为何值时,此方程是一元二次方程
五、综合题
13.向阳中学数学兴趣小组对关于x的方程(m+1) +(m﹣2)x﹣1=0提出了下列问题:
(1)是否存在m的值,使方程为一元二次方程?若存在,求出m的值,并解此方程;
(2)是否存在m的值,使方程为一元一次方程?若存在,求出m的值,并解此方程.
14.观察下列一组方程:①x2﹣x=0;②x2﹣3x+2=0;③x2﹣5x+6=0;④x2﹣7x+12=0;…它们的根有一定的规律,都是两个连续的自然数,我们称这类一元二次方程为“连根一元二次方程”.
(1)若x2+kx+56=0也是“连根一元二次方程”,写出k的值,并解这个一元二次方程;
(2)请写出第n个方程和它的根.
六、实践探究题
15.为美化市容,某广场要在人行雨道上用10×20的灰、白两色的广场砖铺设图案,设计人员画出的一些备选图案如图所示.
[观察思考]
图1灰砖有1块,白砖有8块;图2灰砖有4块,白砖有12块;以此类推.
[规律总结]
(1)图4灰砖有 块,白砖有 块;图n灰砖有 块时,白砖有 块;
(2)[问题解决]
是否存在白砖数恰好比灰砖数少1的情形,请通过计算说明你的理由.
答案解析部分
1.【答案】B
【知识点】一元二次方程的定义及相关的量
2.【答案】C
【知识点】一元二次方程的定义及相关的量
3.【答案】A
【知识点】一元二次方程的定义及相关的量
4.【答案】C
【知识点】列一元二次方程
5.【答案】B
【知识点】一元二次方程的定义及相关的量
6.【答案】
【知识点】一元二次方程的定义及相关的量
7.【答案】-1
【知识点】一元二次方程的定义及相关的量
8.【答案】m=1或m>2
【知识点】一元二次方程的定义及相关的量
9.【答案】解:因为是关于x的一元二次方程,这个方程一定有一个二次项,则(m+1)x|m|+1一定是此二次项.
所以得到 ,
解得m=1.
【知识点】一元二次方程的定义及相关的量
10.【答案】解:原式化简得
n满足一元二次方程n2+n-2=0, n=1或n= -2.当n=1时,n-1=0,分式无意义,故n=1舍去.当n= -2
时,原式=
【知识点】分式的基本性质;一元二次方程的定义及相关的量
11.【答案】解:设道路的宽为x米,草坪的长为(22-x)米,宽为(17-x)米,
由题意得:
该方程是一元二次方程,
化为一般形式为:
【知识点】一元二次方程的定义及相关的量;列一元二次方程
12.【答案】(1)解:∵(m+3)(m-3)x2+(m+3)x+2=0,
∴如果此方程是一元一次方程,
则
解得m=3,
即当m=3时,此方程是一元一次方程.
(2)解:∵(m+3)(m-3)x2+(m+3)x+2=0,
∴如果此方程是一元二次方程,
则(m+3)(m-3)≠0,
解得m≠-3且m≠3,
即当m≠-3且m≠3时,此方程是一元二次方程.
【知识点】一元一次方程的定义;一元二次方程的定义及相关的量
13.【答案】(1)解:根据一元二次方程的定义可得 ,解得m=1,此时方程为2x2-x-1=0,解得x1=1,x2=- ;
(2)解:由题可知m2+1=1或m+1=0时方程为一元一次方程
当m2+1=1时,解得m=0,此时方程为-x-1=0,解得x=-1,
当m+1=0时,解得m=-1,此时方程为-3x-1=0,解得x=- .
【知识点】一元一次方程的定义;一元二次方程的定义及相关的量
14.【答案】(1)解:由题意可得:k=﹣15,
则原方程为:x2﹣15x+56=0,
则(x﹣7)(x﹣8)=0,
解得:x1=7,x2=8
(2)解:第n个方程为:x2﹣2(n﹣1)x+n(n﹣1)=0,
(x﹣n)(x﹣n+1)=0,
解得:x1=n﹣1,x2=n
【知识点】一元二次方程的定义及相关的量
15.【答案】(1)16;20;n2;(4n+4)
(2)解:存在,理由如下:根据题意得:n2-(4n+4)=1,
解得:n=-1(舍去)或n=5.
【知识点】列一元二次方程
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【北师大版九上同步练习】 2.1认识一元二次方程
一、单选题
1.一元二次方程的一次项系数是( )
A. B.-2 C.-7 D.2
2.若方程化为一元二次方程的一般形式后不含一次项,则的值为( )
A.0 B. C.3 D.
3.若关于的方程是一元二次方程,则的值是( )
A.-1 B.2 C.-1或3 D.3
4.《九章算术》是中国传统数学最重要的著作,书中有一个关于门和竹竿的问题,简译为:今有一扇门,不知门的高和宽.另有一竹竿,也不知竹竿的长短.竹竿横着放时比门的宽长4尺,竹竿竖着放时比门的高长2尺,竹竿斜着放时与门的对角线恰好相等,求门的对角线长.若设门的对角线长为尺,则可列方程为( )
A. B.
C. D.
5.下列各式中是一元二次方程的是( )
A.x2+x=2y B.x2=1 C.ax2+bx+c=0 D.x2﹣2=x2+1
二、填空题
6.将化成一元二次方程的一般形式的结果为+ =0.
7.若关于x的方程是一元二次方程,则m的值为
8.关于x的方程(1-m2)x2+2mx-1=0的所有根都是比1小的正实数,则实数m的取值范围是 .
三、计算题
9.若(m+1) +6-2=0是关于x的一元二次方程,求m的值.
10.已知分式 ,若n满足一元二次方程n2+n-2=0,先化简原分式,再求值。
四、解答题
11.如图,在一块长为,宽为的长方形地面上,要修建同样宽的两条互相垂直的道路.两条道路各与长方形的一条边平行,剩余部分种上草坪.已知草坪的面积为,设道路宽为,写出关于的方程.该方程是一元二次方程吗 如果是,把它化成一元二次方程的一般形式.
12.已知关于x的方程(m+3)(m-3)x2+(m+3)x+2=0.
(1)当m为何值时,此方程是一元一次方程
(2)当m为何值时,此方程是一元二次方程
五、综合题
13.向阳中学数学兴趣小组对关于x的方程(m+1) +(m﹣2)x﹣1=0提出了下列问题:
(1)是否存在m的值,使方程为一元二次方程?若存在,求出m的值,并解此方程;
(2)是否存在m的值,使方程为一元一次方程?若存在,求出m的值,并解此方程.
14.观察下列一组方程:①x2﹣x=0;②x2﹣3x+2=0;③x2﹣5x+6=0;④x2﹣7x+12=0;…它们的根有一定的规律,都是两个连续的自然数,我们称这类一元二次方程为“连根一元二次方程”.
(1)若x2+kx+56=0也是“连根一元二次方程”,写出k的值,并解这个一元二次方程;
(2)请写出第n个方程和它的根.
六、实践探究题
15.为美化市容,某广场要在人行雨道上用10×20的灰、白两色的广场砖铺设图案,设计人员画出的一些备选图案如图所示.
[观察思考]
图1灰砖有1块,白砖有8块;图2灰砖有4块,白砖有12块;以此类推.
[规律总结]
(1)图4灰砖有 块,白砖有 块;图n灰砖有 块时,白砖有 块;
(2)[问题解决]
是否存在白砖数恰好比灰砖数少1的情形,请通过计算说明你的理由.
答案解析部分
1.【答案】B
【知识点】一元二次方程的定义及相关的量
2.【答案】C
【知识点】一元二次方程的定义及相关的量
3.【答案】A
【知识点】一元二次方程的定义及相关的量
4.【答案】C
【知识点】列一元二次方程
5.【答案】B
【知识点】一元二次方程的定义及相关的量
6.【答案】
【知识点】一元二次方程的定义及相关的量
7.【答案】-1
【知识点】一元二次方程的定义及相关的量
8.【答案】m=1或m>2
【知识点】一元二次方程的定义及相关的量
9.【答案】解:因为是关于x的一元二次方程,这个方程一定有一个二次项,则(m+1)x|m|+1一定是此二次项.
所以得到 ,
解得m=1.
【知识点】一元二次方程的定义及相关的量
10.【答案】解:原式化简得
n满足一元二次方程n2+n-2=0, n=1或n= -2.当n=1时,n-1=0,分式无意义,故n=1舍去.当n= -2
时,原式=
【知识点】分式的基本性质;一元二次方程的定义及相关的量
11.【答案】解:设道路的宽为x米,草坪的长为(22-x)米,宽为(17-x)米,
由题意得:
该方程是一元二次方程,
化为一般形式为:
【知识点】一元二次方程的定义及相关的量;列一元二次方程
12.【答案】(1)解:∵(m+3)(m-3)x2+(m+3)x+2=0,
∴如果此方程是一元一次方程,
则
解得m=3,
即当m=3时,此方程是一元一次方程.
(2)解:∵(m+3)(m-3)x2+(m+3)x+2=0,
∴如果此方程是一元二次方程,
则(m+3)(m-3)≠0,
解得m≠-3且m≠3,
即当m≠-3且m≠3时,此方程是一元二次方程.
【知识点】一元一次方程的定义;一元二次方程的定义及相关的量
13.【答案】(1)解:根据一元二次方程的定义可得 ,解得m=1,此时方程为2x2-x-1=0,解得x1=1,x2=- ;
(2)解:由题可知m2+1=1或m+1=0时方程为一元一次方程
当m2+1=1时,解得m=0,此时方程为-x-1=0,解得x=-1,
当m+1=0时,解得m=-1,此时方程为-3x-1=0,解得x=- .
【知识点】一元一次方程的定义;一元二次方程的定义及相关的量
14.【答案】(1)解:由题意可得:k=﹣15,
则原方程为:x2﹣15x+56=0,
则(x﹣7)(x﹣8)=0,
解得:x1=7,x2=8
(2)解:第n个方程为:x2﹣2(n﹣1)x+n(n﹣1)=0,
(x﹣n)(x﹣n+1)=0,
解得:x1=n﹣1,x2=n
【知识点】一元二次方程的定义及相关的量
15.【答案】(1)16;20;n2;(4n+4)
(2)解:存在,理由如下:根据题意得:n2-(4n+4)=1,
解得:n=-1(舍去)或n=5.
【知识点】列一元二次方程
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
