数学人教A版(2019)必修第一册2.2基本不等式 课件(共37张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册2.2基本不等式 课件(共37张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-10 00:00:00 | ||
图片预览











文档简介
(共37张PPT)
基本不等式
一般地,对于任意实数a、b,总有
当且仅当a=b时,等号成立
文字叙述为:
两数的平方和不小于它们积的2倍.
适用范围:
a,b∈R
复习提问
重要不等式
替换后得到:
即:
即:
你能用不等式的性质直接推导这个不等式吗?
学习新知
证明:要证
只要证
①
要证①,只要证
②
要证②,只要证
③
显然, ③是成立的.当且仅当a=b时, ③中的等号成立.
分析法
证明不等式:
学习新知
基本不等式
1.如何理解“基本”呢?
对象少;
关系简;
应用广.
2.基本不等式的几何解释
如图, AB是圆的直径, 点C是AB上一点, AC=a, BC=b. 过点C作垂直于AB的弦DE,连接AD、BD.
易证Rt△ACD∽Rt△DCB,则
A
B
C
D
E
a
b
而这个圆的半径为 , 显然会大于或等于CD, 即
其中当且仅当点C与圆心重合,即a=b时, 等号成立.
特别地,若a>0,b>0,则
≥
通常我们把上式写作:
当且仅当a=b时取等号,这个不等式就叫做基本不等式.
基本不等式
在数学中,我们把 叫做正数a,b的算术平均数,
叫做正数a,b的几何平均数;
文字叙述为:
两个正数的算术平均数不小于它们的几何平均数.
适用范围:
a>0,b>0
学习新知
适用范围
文字叙述
“=”成立条件
a=b
a=b
两个正数的算术平均数不小于它们的几何平均数
两数的平方和不小于它们积的2倍
a,b∈R
a>0,b>0
填表比较:
注意从不同角度认识基本不等式
学习新知
基本不等式的应用
例1.已知x>0 ,求 的最小值和此时x的取值.
典型例题
基本不等式的应用
例1.已知x>0 ,求 的最小值和此时x的取值.
典型例题
变式1:把 改为 成立吗?
变式2:把 改为 成立吗?
不成立
不成立
练习课本P46T3,4,5
基本不等式的运用
典型例题
例2.已知 x, y 都是正数,求证:
(1)如果积 xy 等于定值P ,那么当 x=y 时,和x+y有最小值2 P.
(2)如果和x+y等于定值S ,那么当 x=y 时,积xy有最大值 S2.
1
4
积定和最小,
和定积最大.
一正、
二定、
三相等
练习课本P46T1,2,5
①各项皆为正数;
②和或积为定值;
③注意等号成立的条件.
一“正”
二“定”
三“相等”
利用基本不等式求最值时,要注意
归纳总结
已知 x, y 都是正数,求证:
(1)如果积 xy 等于定值P ,那么当 x=y 时,和x+y有最小值2 P.
(2)如果和x+y等于定值S ,那么当 x=y 时,积xy有最大值 S2.
1
4
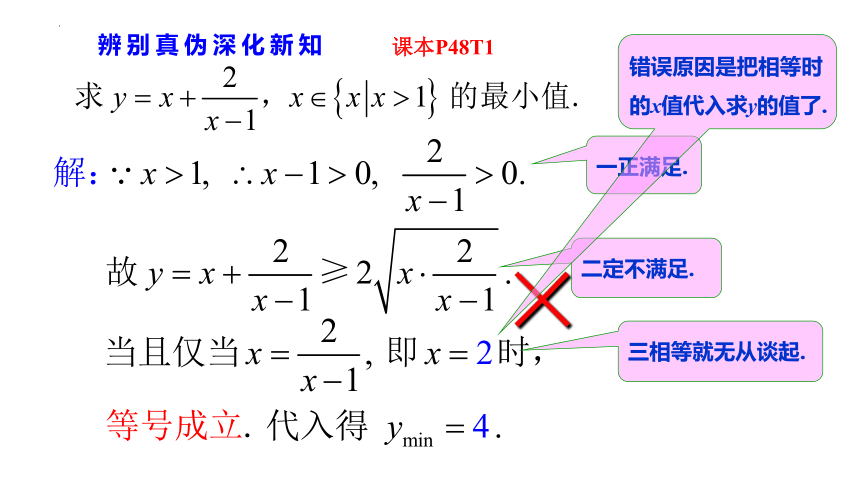
辨别真伪深化新知
×
一正满足.
二定不满足.
三相等就无从谈起.
错误原因是把相等时的x值代入求y的值了.
课本P48T1
去伪存真强化三识
一正满足.
二定也满足.
三相等也能成立.
课本P48T1
求最值时注意把握 “一正,二定,三相等”
3. 利用基本不等式求最值
1. 重要不等式
即时小结
2. 基本不等式
已知 x, y 都是正数,求证:
(1)如果积 xy 等于定值P ,那么当 x=y 时,和x+y有最小值2 P.
(2)如果和x+y等于定值S ,那么当 x=y 时,积xy有最大值 S2.
1
4
1.已知x>0, y>0, xy=24, 求4x+6y的最小值,并说明此时x,y的值.
当x=6,y=4时,最小值为48
2.已知x<0,求 的最大值.
巩固练习
3. 求x> -1时, 的最小值.
解: ∵ x>-1, ∴x+1>0.
=(x +1)+ -1
1
x+1
∴ x +
1
x+1
=1,
≥2 (x+1) -1
1
x+1
当且仅当 取“=”号.
∴当 x=0 时, 取最小值是 1.
x+1= , 即 x=0 时,
1
x+1
强化重点突破难点
提高练习
2. 已知x>0,y>0,且x+2y=1,求 的最小值.
3.已知x,y为正数,且2x+8y=xy,则x+y 的最小值是___.
18
4.已知x,y为正数,且x+y+3=xy,则xy 的取值范围是___.课本P58T5
xy≥9
强化重点突破难点
基本不等式
2.两个不等式中 “当且仅当a=b时,等号成立”这句话应从两方面来理解:
(1)当a=b时,等号成立.其含义为:如果a=b,那么
(2)仅当a=b时,等号成立.其含义为:如果 ,那么a=b.
综合起来,“当且仅当a=b时,等号成立.”
其含义是: a=b等价于
对于重要不等式 以及基本不等式 ,要注意
1.两不等式成立的条件不一样
深刻认识理解新知
充要条件.
问题解决应用新知
证明:
(1)因a,b均为正数,由基本不等式,可知
也即
当且仅当 时,等号成立
该不等式的几何解释
如图1,设
交⊙O上半圆于D,过C作
交OD于E,
在Rt△OCD中,由射影定理可知
即
由DC≥DE,得
当且仅当 时,等号成立
问题解决应用新知
(2)因为
不等式两边同时加上
由于两边都是正数,所以两边开方得:
问题解决应用新知
当且仅当 时,等号成立
该不等式的几何解释
当且仅当 时,等号成立
如图2,设
交⊙O上半圆于F,
由FC≥OF,得
问题解决应用新知
其中当且仅当a=b时取等号.
重要结论
问题解决应用新知
算术平均数
几何平均数
平方平均数
调和平均数
两个正数的倒数的算术平均数的倒数.
两个正数的平方的算术平均数的算术平方根.
(1)(2)(3)
练习:设a>0,b>0,给出下列不等式
其中恒成立的 .
课堂练习巩固新知
多项选择题是新高考新增加的题型
例2 已知a,b都是正实数,且ab=2,求证:(1+2a)(1+b)≥9.
求实际问题中最值的一般思路
(1)先读懂题意,设出变量,理清思路,列出函数关系式.
(2)把实际问题抽象成函数的最大值或最小值问题.
(3)在定义域内,求函数的最大值或最小值时,一般先考虑基本不等式,当基本不等式求最值的条件不具备时,再考虑函数的单调性.
(4)正确写出答案.
方法技巧
归纳总结概括新知
基本不等式
应用
证明
几何解释
代数认识
1.本节知识结构
归纳总结概括新知
2.用 基本不等式 能解决简单
的 函数最值 问题. 应注意:
一 正 (条件)
二 定
(前提)
三 相等
(保证)
积定相等和最小;
和定相等积最大.
归纳总结概括新知
1.知识层面上:基本不等式,函数最值
2.方法策略上:数形结合,变式训练,适度配凑
3.思想层面上:等价转化,模型构造,同化思维
4.意志品质上:逢山开道,遇水搭桥,知难而进
基本不等式
一般地,对于任意实数a、b,总有
当且仅当a=b时,等号成立
文字叙述为:
两数的平方和不小于它们积的2倍.
适用范围:
a,b∈R
复习提问
重要不等式
替换后得到:
即:
即:
你能用不等式的性质直接推导这个不等式吗?
学习新知
证明:要证
只要证
①
要证①,只要证
②
要证②,只要证
③
显然, ③是成立的.当且仅当a=b时, ③中的等号成立.
分析法
证明不等式:
学习新知
基本不等式
1.如何理解“基本”呢?
对象少;
关系简;
应用广.
2.基本不等式的几何解释
如图, AB是圆的直径, 点C是AB上一点, AC=a, BC=b. 过点C作垂直于AB的弦DE,连接AD、BD.
易证Rt△ACD∽Rt△DCB,则
A
B
C
D
E
a
b
而这个圆的半径为 , 显然会大于或等于CD, 即
其中当且仅当点C与圆心重合,即a=b时, 等号成立.
特别地,若a>0,b>0,则
≥
通常我们把上式写作:
当且仅当a=b时取等号,这个不等式就叫做基本不等式.
基本不等式
在数学中,我们把 叫做正数a,b的算术平均数,
叫做正数a,b的几何平均数;
文字叙述为:
两个正数的算术平均数不小于它们的几何平均数.
适用范围:
a>0,b>0
学习新知
适用范围
文字叙述
“=”成立条件
a=b
a=b
两个正数的算术平均数不小于它们的几何平均数
两数的平方和不小于它们积的2倍
a,b∈R
a>0,b>0
填表比较:
注意从不同角度认识基本不等式
学习新知
基本不等式的应用
例1.已知x>0 ,求 的最小值和此时x的取值.
典型例题
基本不等式的应用
例1.已知x>0 ,求 的最小值和此时x的取值.
典型例题
变式1:把 改为 成立吗?
变式2:把 改为 成立吗?
不成立
不成立
练习课本P46T3,4,5
基本不等式的运用
典型例题
例2.已知 x, y 都是正数,求证:
(1)如果积 xy 等于定值P ,那么当 x=y 时,和x+y有最小值2 P.
(2)如果和x+y等于定值S ,那么当 x=y 时,积xy有最大值 S2.
1
4
积定和最小,
和定积最大.
一正、
二定、
三相等
练习课本P46T1,2,5
①各项皆为正数;
②和或积为定值;
③注意等号成立的条件.
一“正”
二“定”
三“相等”
利用基本不等式求最值时,要注意
归纳总结
已知 x, y 都是正数,求证:
(1)如果积 xy 等于定值P ,那么当 x=y 时,和x+y有最小值2 P.
(2)如果和x+y等于定值S ,那么当 x=y 时,积xy有最大值 S2.
1
4
辨别真伪深化新知
×
一正满足.
二定不满足.
三相等就无从谈起.
错误原因是把相等时的x值代入求y的值了.
课本P48T1
去伪存真强化三识
一正满足.
二定也满足.
三相等也能成立.
课本P48T1
求最值时注意把握 “一正,二定,三相等”
3. 利用基本不等式求最值
1. 重要不等式
即时小结
2. 基本不等式
已知 x, y 都是正数,求证:
(1)如果积 xy 等于定值P ,那么当 x=y 时,和x+y有最小值2 P.
(2)如果和x+y等于定值S ,那么当 x=y 时,积xy有最大值 S2.
1
4
1.已知x>0, y>0, xy=24, 求4x+6y的最小值,并说明此时x,y的值.
当x=6,y=4时,最小值为48
2.已知x<0,求 的最大值.
巩固练习
3. 求x> -1时, 的最小值.
解: ∵ x>-1, ∴x+1>0.
=(x +1)+ -1
1
x+1
∴ x +
1
x+1
=1,
≥2 (x+1) -1
1
x+1
当且仅当 取“=”号.
∴当 x=0 时, 取最小值是 1.
x+1= , 即 x=0 时,
1
x+1
强化重点突破难点
提高练习
2. 已知x>0,y>0,且x+2y=1,求 的最小值.
3.已知x,y为正数,且2x+8y=xy,则x+y 的最小值是___.
18
4.已知x,y为正数,且x+y+3=xy,则xy 的取值范围是___.课本P58T5
xy≥9
强化重点突破难点
基本不等式
2.两个不等式中 “当且仅当a=b时,等号成立”这句话应从两方面来理解:
(1)当a=b时,等号成立.其含义为:如果a=b,那么
(2)仅当a=b时,等号成立.其含义为:如果 ,那么a=b.
综合起来,“当且仅当a=b时,等号成立.”
其含义是: a=b等价于
对于重要不等式 以及基本不等式 ,要注意
1.两不等式成立的条件不一样
深刻认识理解新知
充要条件.
问题解决应用新知
证明:
(1)因a,b均为正数,由基本不等式,可知
也即
当且仅当 时,等号成立
该不等式的几何解释
如图1,设
交⊙O上半圆于D,过C作
交OD于E,
在Rt△OCD中,由射影定理可知
即
由DC≥DE,得
当且仅当 时,等号成立
问题解决应用新知
(2)因为
不等式两边同时加上
由于两边都是正数,所以两边开方得:
问题解决应用新知
当且仅当 时,等号成立
该不等式的几何解释
当且仅当 时,等号成立
如图2,设
交⊙O上半圆于F,
由FC≥OF,得
问题解决应用新知
其中当且仅当a=b时取等号.
重要结论
问题解决应用新知
算术平均数
几何平均数
平方平均数
调和平均数
两个正数的倒数的算术平均数的倒数.
两个正数的平方的算术平均数的算术平方根.
(1)(2)(3)
练习:设a>0,b>0,给出下列不等式
其中恒成立的 .
课堂练习巩固新知
多项选择题是新高考新增加的题型
例2 已知a,b都是正实数,且ab=2,求证:(1+2a)(1+b)≥9.
求实际问题中最值的一般思路
(1)先读懂题意,设出变量,理清思路,列出函数关系式.
(2)把实际问题抽象成函数的最大值或最小值问题.
(3)在定义域内,求函数的最大值或最小值时,一般先考虑基本不等式,当基本不等式求最值的条件不具备时,再考虑函数的单调性.
(4)正确写出答案.
方法技巧
归纳总结概括新知
基本不等式
应用
证明
几何解释
代数认识
1.本节知识结构
归纳总结概括新知
2.用 基本不等式 能解决简单
的 函数最值 问题. 应注意:
一 正 (条件)
二 定
(前提)
三 相等
(保证)
积定相等和最小;
和定相等积最大.
归纳总结概括新知
1.知识层面上:基本不等式,函数最值
2.方法策略上:数形结合,变式训练,适度配凑
3.思想层面上:等价转化,模型构造,同化思维
4.意志品质上:逢山开道,遇水搭桥,知难而进
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
