第1章 空间向量与立体几何 测评 同步练(含解析) 2024-2025学年高二数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 第1章 空间向量与立体几何 测评 同步练(含解析) 2024-2025学年高二数学人教A版(2019)选择性必修第一册 |

|
|
| 格式 | docx | ||
| 文件大小 | 858.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-10 00:00:00 | ||
图片预览




文档简介
第一章测评
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在长方体ABCD-A1B1C1D1中,等于( )
A. B.
C. D.
2.已知a=(2,-1,3),b=(-1,4,-2),c=(1,3,λ),若a,b,c三向量共面,则实数λ等于( )
A.1 B.2
C.3 D.4
3.已知空间向量a=(1,n,2),b=(-2,1,2),若2a-b与b垂直,则|a|等于( )
A. B.
C. D.
4.[2024江苏淮安高二统考期末]已知四棱锥P-ABCD的底面为正方形,PA⊥平面ABCD,PA=AB=1,点E是BC的中点,则点E到直线PD的距离是( )
A. B.
C. D.
5.[2024江苏徐州高二统考]在正四面体APBC中,过点A作平面PBC的垂线,垂足为Q,点M满足,则=( )
A. B.
C. D.
6.如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AB⊥AD,BC∥AD,且AB=BC=2, AD=3,PA⊥平面ABCD,且PA=2,则PB与平面PCD所成角的正弦值为( )
A. B.
C. D.
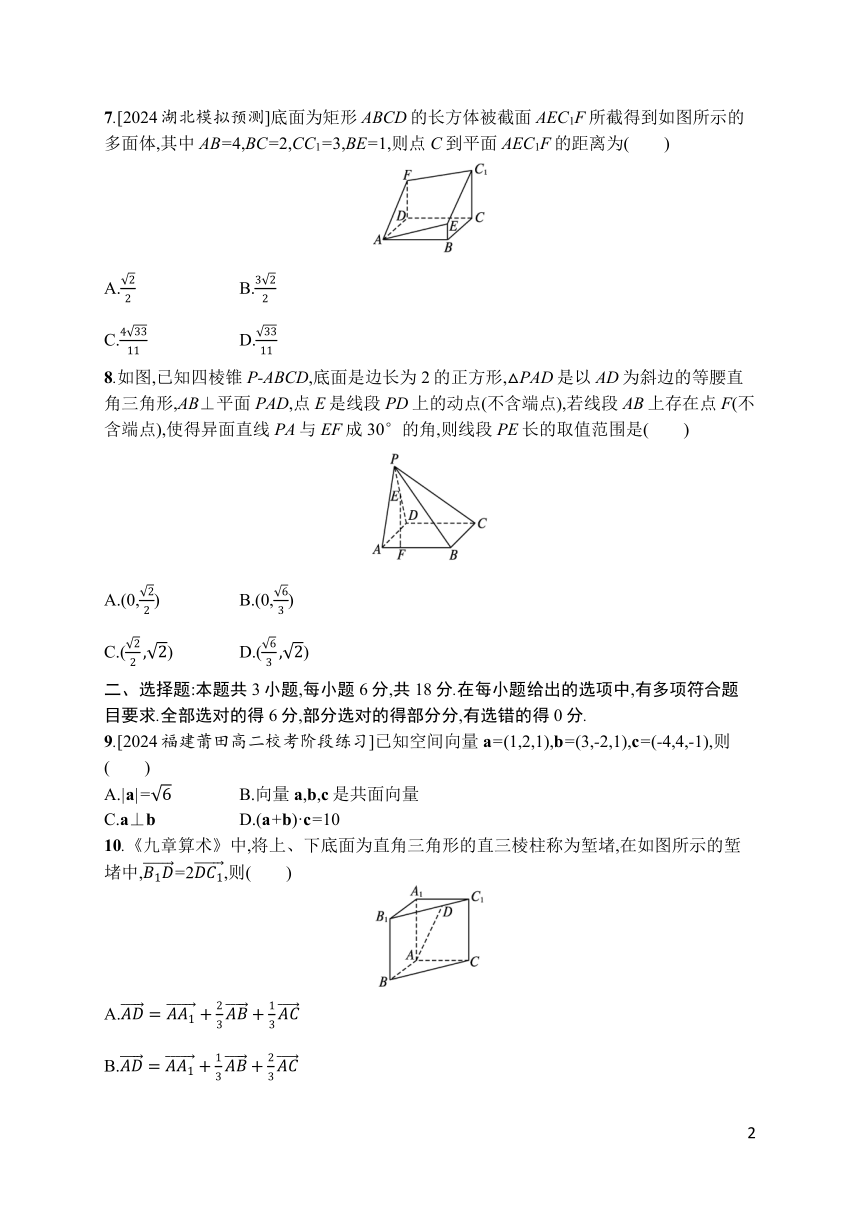
7.[2024湖北模拟预测]底面为矩形ABCD的长方体被截面AEC1F所截得到如图所示的多面体,其中AB=4,BC=2,CC1=3,BE=1,则点C到平面AEC1F的距离为( )
A. B.
C. D.
8.如图,已知四棱锥P-ABCD,底面是边长为2的正方形,△PAD是以AD为斜边的等腰直角三角形,AB⊥平面PAD,点E是线段PD上的动点(不含端点),若线段AB上存在点F(不含端点),使得异面直线PA与EF成30°的角,则线段PE长的取值范围是( )
A.(0,) B.(0,)
C.() D.()
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.[2024福建莆田高二校考阶段练习]已知空间向量a=(1,2,1),b=(3,-2,1),c=(-4,4,-1),则( )
A.|a|= B.向量a,b,c是共面向量
C.a⊥b D.(a+b)·c=10
10.《九章算术》中,将上、下底面为直角三角形的直三棱柱称为堑堵,在如图所示的堑堵中,=2,则( )
A.
B.
C.向量在向量上的投影向量为
D.向量在向量上的投影向量为
11.将正方形ABCD沿对角线BD翻折,使平面ABD与平面BCD的夹角为,以下四个结论正确的是( )
A.AC⊥BD
B.△ACD是等边三角形
C.直线AB与平面BCD所成的角为
D.AB与CD所成的角为
三、填空题:本题共3小题,每小题5分,共15分.
12.空间向量a=(2,2,-1)的单位向量的坐标是 .
13.已知a=(3,-2,-3),b=(-1,x-1,1),且向量a与b的夹角为钝角,则x的取值范围是 .
14.如图,正方形ABCD,ABEF的边长都是1,而且平面ABCD,ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)已知a=(x,4,1),b=(-2,y,-1),c=(3,-2,z),a∥b,b⊥c,求:
(1)a,b,c;
(2)向量a+c与b+c夹角的余弦值.
16.(15分)如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD, AB=AD=2,CD=4,M为CE的中点.求证:
(1)BM∥平面ADEF;
(2)BC⊥平面BDE.
17.(15分)如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥平面ABCD,AB∥DC,AB⊥AD,AD=CD=2,AA1=AB=4,E为棱AA1的中点.
(1)证明:BC⊥EC1.
(2)设=λ(0<λ<1),若点C1到平面BB1M的距离为,求λ.
18.(17分)如图1,四边形ABCD为等腰梯形,AB=2,AD=DC=CB=1,将△ADC沿AC折起,E为AB的中点,连接DE,DB,如图2,BC⊥AD.
(1)求线段BD的长;
(2)求直线BD与平面CDE所成的角的正弦值.
图1
图2
19.(17分)如图,在四棱锥S-ABCD中,∠DAB=∠ADC=2∠ABD=2∠BCD=90°, CB=BD=2,SB=SD=,SD⊥BC.
(1)求证:平面SBD⊥平面SBC;
(2)若点P在线段SC上,且=λ,平面ABP与平面SBD的夹角为60°,求λ的值.
答案:
1.A .
2.A 若向量a,b,c共面,则c=xa+yb,其中x,y∈R,
即(1,3,λ)=(2x,-x,3x)+(-y,4y,-2y)=(2x-y,-x+4y,3x-2y),
则有
解得
3.B 因为a=(1,n,2),b=(-2,1,2),
所以2a-b=(4,2n-1,2).
因为2a-b与b垂直,
所以(2a-b)·b=0,
所以-8+2n-1+4=0,
解得n=,
所以a=(1,,2),
所以|a|=.
4.D 以A为原点,AB,AD,AP所在直线为x轴、y轴、z轴建立如图所示的空间直角坐标系,则P(0,0,1),D(0,1,0),E,
所以=(0,1,-1),,
所以||=,||==-,
所以点E到直线PD的距离是.
故选D.
5.B 由题知,在正四面体APBC中,
因为AQ⊥平面PBC,
所以Q是△PBC的中心.
连接PQ,则),
所以×()
=)=.
故选B.
6.C 依题意,以A为坐标原点,分别以AB,AD,AP所在直线为x轴、y轴、z轴建立如图所示的空间直角坐标系,
因为AB=BC=2,AD=3,PA=2,
则P(0,0,2),B(2,0,0),C(2,2,0),D(0,3,0),
从而=(2,0,-2),=(2,2,-2),=(0,3,-2),
设平面PCD的法向量为n=(a,b,c),
则
不妨取c=3,则a=1,b=2,
所以平面PCD的一个法向量为n=(1,2,3),
设PB与平面PCD所成角为θ,
则sin θ=|cos<,n>|==.
7.C 以D为原点,DA,DC,DF所在直线为x轴、y轴、z轴建立如图所示的空间直角坐标系,
则D(0,0,0),A(2,0,0),C(0,4,0),E(2,4,1),C1(0,4,3),
∴=(-2,4,3),=(0,4,1).
设平面AEC1F的法向量为n=(x,y,z),
由
令z=1,则x=1,y=-,
所以n=.
又=(0,0,3),
∴点C到平面AEC1F的距离d=.
故选C.
8.B 由△PAD是以AD为斜边的等腰直角三角形,AB⊥平面PAD,底面ABCD为正方形,取AD的中点G,建立如图所示的空间直角坐标系,
则G(0,0,0),A(1,0,0),D(-1,0,0),B(1,2,0),P(0,0,1),设F(1,y,0),0设=x=x(1,0,1)=(x,0,x),0故E(x-1,0,x),=(2-x,y,-x),=(x-1,0,x-1).
又=(1,0,-1),异面直线PA与EF成30°的角,
故=||||cos 30°,
即2=,
即(x-1)2=y2,0∴(x-1)2∈(0,),
∴||2=2(x-1)2∈(0,),
∴||∈(0,).
9.ABC 由题得,|a|=,故A正确;
设a=mb+nc,
即
解得
即a=3b+2c,所以向量a,b,c共面,故B正确;
因为a·b=3-4+1=0,
所以a⊥b,故C正确;
(a+b)·c=(4,0,2)·(-4,4,-1)=-18,故D错误.
故选ABC.
10.BD 因为
)=,故A不正确,B正确.
如图所示,过点D作DU⊥BC,过点U作VU⊥AB,UW⊥AC,
故向量在向量上的投影向量为,向量在向量上的投影向量为,
由题意易得,故,故C不正确,D正确.
故选BD.
11.ABD 如图所示,以BD的中点O为坐标原点,OD,OA,OC所在直线分别为x轴、y轴、z轴,建立空间直角坐标系Oxyz,
设正方形ABCD的边长为,
则D(1,0,0),B(-1,0,0),C(0,0,1),A(0,1,0),
所以=(0,-1,1),=(2,0,0),=0.
故AC⊥BD,A正确.
又||=,||=,||=,
所以△ACD为等边三角形,B正确.
对于C,为平面BCD的一个法向量,=(-1,-1,0),
cos<>==-=-.
因为直线与平面所成的角的范围是[0,],
所以AB与平面BCD所成的角为,故C错误.
又cos<>==-,
因为异面直线所成的角为锐角或直角,所以AB与CD所成的角为,故D正确.
12. 由题可得|a|==3,
∴向量a的单位向量的坐标为(2,2,-1)=.
13. 因为向量a与b的夹角为钝角,
所以a·b=-3-2(x-1)-3<0,
解得x>-2.
由题意得a与b不共线,则,
解得x≠,
所以x的取值范围是.
14. 建立空间直角坐标系如图所示,则A(1,0,0),F(1,1,0),C(0,0,1).
因为CM=BN=a(0所以Ma,0,1-a,Na,a,0,
所以=0,a,a-1.
所以||=,
即MN的长为.
当a=时,||min=,即M,N分别为AC,BF的中点时,MN的长最小,最小值为.
15.解 (1)因为a∥b,易知y≠0,
所以,
解得x=2,y=-4,
则a=(2,4,1),b=(-2,-4,-1).
又b⊥c,所以b·c=0,
即-6+8-z=0,
解得z=2,于是c=(3,-2,2).
(2)由(1)得a+c=(5,2,3),b+c=(1,-6,1),
设向量a+c与b+c的夹角为θ,
因为cos θ==-,
所以向量a+c与b+c夹角的余弦值为-.
16.证明 ∵平面ADEF⊥平面ABCD,平面ADEF∩平面ABCD=AD,AD⊥ED,ED 平面ADEF,
∴ED⊥平面ABCD.
以D为原点,DA,DC,DE所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
则D(0,0,0),A(2,0,0),B(2,2,0),C(0,4,0),E(0,0,2),F(2,0,2).
(1)∵M为EC的中点,
∴M(0,2,1),
则=(-2,0,1),=(-2,0,0),=(0,0,2),
∴,故共面.
又BM 平面ADEF,
∴BM∥平面ADEF.
(2)=(-2,2,0),=(2,2,0),=(0,0,2),
∵=-4+4=0,∴BC⊥DB.
又=0,
∴BC⊥DE.
又DE∩DB=D,DE,DB 平面BDE,
∴BC⊥平面BDE.
17.(1)证明 以A为原点,AD,AA1,AB所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
则B(0,0,4),D(2,0,0),C(2,0,2),E(0,2,0),C1(2,4,2),B1(0,4,4),所以=(2,0,-2),=(2,2,2),
所以=2×2+0+2×(-2)=0,
所以,
即BC⊥EC1.
(2)解 因为=(0,4,0),=(-2,2,-2),
所以+λ=(2-2λ,2λ,-2-2λ).
设平面BB1M的法向量为n=(x,y,z),
所以
令x=1+λ,
则y=0,z=1-λ,得n=(1+λ,0,1-λ).
因为=(2,0,-2),
所以点C1到平面BB1M的距离d=,解得λ=.
18.解 (1)在题图1中作CH⊥AB,交AB于点H(图略),则BH=,
∴∠B=,∠D=,
AC=,
∴AC2+BC2=AB2,
∴BC⊥AC,
∴在题图2中,AC⊥BC.
又AD⊥BC,AD∩AC=A,AD,AC 平面ACD,
∴BC⊥平面ACD,
取AC中点F,连接DF,FE,则FA,FE,FD两两垂直,
以F为坐标原点,建立空间直角坐标系,如图,
D(0,0,),B(-,1,0),
∴线段BD的长为||=.
(2)=(,-1,),C(-,0,0),E(0,,0),=(,0,),=(,0),
设平面CDE的法向量为n=(x,y,z),
则取x=1,
得n=(1,-,-).
设直线BD与平面CDE所成的角为θ,
则直线BD与平面CDE所成的角的正弦值为
sin θ=.
19.(1)证明 因为CB=BD,2∠BCD=90°,故∠CBD=90°,
所以BC⊥BD.
又SD⊥BC,SD∩BD=D,SD,BD 平面SBD,
所以BC⊥平面SBD.
因为BC 平面SBC,
所以平面SBD⊥平面SBC.
(2)解 由(1)可得,平面ABCD⊥平面SBD,
设E为BD的中点,连接SE,
因为SB=SD=,
所以SE⊥BD,
故SE⊥平面ABCD.
如图,建立空间直角坐标系Axyz,则A(0,0,0),B(0,2,0),C(2,4,0),S(1,1,2).
因为=λ,
所以P(2-λ,4-3λ,2λ),
易得平面SBD的一个法向量为=(2,2,0).
设n=(x,y,z)为平面ABP的法向量,
=(0,2,0),=(2-λ,4-3λ,2λ),
由
不妨取n=(2λ,0,λ-2).
因为平面SBD与平面ABP的夹角为60°,
所以|cos<,n>|=,且λ>0,
解得λ=或λ=-2(舍去),
故λ的值为.
14
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在长方体ABCD-A1B1C1D1中,等于( )
A. B.
C. D.
2.已知a=(2,-1,3),b=(-1,4,-2),c=(1,3,λ),若a,b,c三向量共面,则实数λ等于( )
A.1 B.2
C.3 D.4
3.已知空间向量a=(1,n,2),b=(-2,1,2),若2a-b与b垂直,则|a|等于( )
A. B.
C. D.
4.[2024江苏淮安高二统考期末]已知四棱锥P-ABCD的底面为正方形,PA⊥平面ABCD,PA=AB=1,点E是BC的中点,则点E到直线PD的距离是( )
A. B.
C. D.
5.[2024江苏徐州高二统考]在正四面体APBC中,过点A作平面PBC的垂线,垂足为Q,点M满足,则=( )
A. B.
C. D.
6.如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AB⊥AD,BC∥AD,且AB=BC=2, AD=3,PA⊥平面ABCD,且PA=2,则PB与平面PCD所成角的正弦值为( )
A. B.
C. D.
7.[2024湖北模拟预测]底面为矩形ABCD的长方体被截面AEC1F所截得到如图所示的多面体,其中AB=4,BC=2,CC1=3,BE=1,则点C到平面AEC1F的距离为( )
A. B.
C. D.
8.如图,已知四棱锥P-ABCD,底面是边长为2的正方形,△PAD是以AD为斜边的等腰直角三角形,AB⊥平面PAD,点E是线段PD上的动点(不含端点),若线段AB上存在点F(不含端点),使得异面直线PA与EF成30°的角,则线段PE长的取值范围是( )
A.(0,) B.(0,)
C.() D.()
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.[2024福建莆田高二校考阶段练习]已知空间向量a=(1,2,1),b=(3,-2,1),c=(-4,4,-1),则( )
A.|a|= B.向量a,b,c是共面向量
C.a⊥b D.(a+b)·c=10
10.《九章算术》中,将上、下底面为直角三角形的直三棱柱称为堑堵,在如图所示的堑堵中,=2,则( )
A.
B.
C.向量在向量上的投影向量为
D.向量在向量上的投影向量为
11.将正方形ABCD沿对角线BD翻折,使平面ABD与平面BCD的夹角为,以下四个结论正确的是( )
A.AC⊥BD
B.△ACD是等边三角形
C.直线AB与平面BCD所成的角为
D.AB与CD所成的角为
三、填空题:本题共3小题,每小题5分,共15分.
12.空间向量a=(2,2,-1)的单位向量的坐标是 .
13.已知a=(3,-2,-3),b=(-1,x-1,1),且向量a与b的夹角为钝角,则x的取值范围是 .
14.如图,正方形ABCD,ABEF的边长都是1,而且平面ABCD,ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0
15.(13分)已知a=(x,4,1),b=(-2,y,-1),c=(3,-2,z),a∥b,b⊥c,求:
(1)a,b,c;
(2)向量a+c与b+c夹角的余弦值.
16.(15分)如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD, AB=AD=2,CD=4,M为CE的中点.求证:
(1)BM∥平面ADEF;
(2)BC⊥平面BDE.
17.(15分)如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥平面ABCD,AB∥DC,AB⊥AD,AD=CD=2,AA1=AB=4,E为棱AA1的中点.
(1)证明:BC⊥EC1.
(2)设=λ(0<λ<1),若点C1到平面BB1M的距离为,求λ.
18.(17分)如图1,四边形ABCD为等腰梯形,AB=2,AD=DC=CB=1,将△ADC沿AC折起,E为AB的中点,连接DE,DB,如图2,BC⊥AD.
(1)求线段BD的长;
(2)求直线BD与平面CDE所成的角的正弦值.
图1
图2
19.(17分)如图,在四棱锥S-ABCD中,∠DAB=∠ADC=2∠ABD=2∠BCD=90°, CB=BD=2,SB=SD=,SD⊥BC.
(1)求证:平面SBD⊥平面SBC;
(2)若点P在线段SC上,且=λ,平面ABP与平面SBD的夹角为60°,求λ的值.
答案:
1.A .
2.A 若向量a,b,c共面,则c=xa+yb,其中x,y∈R,
即(1,3,λ)=(2x,-x,3x)+(-y,4y,-2y)=(2x-y,-x+4y,3x-2y),
则有
解得
3.B 因为a=(1,n,2),b=(-2,1,2),
所以2a-b=(4,2n-1,2).
因为2a-b与b垂直,
所以(2a-b)·b=0,
所以-8+2n-1+4=0,
解得n=,
所以a=(1,,2),
所以|a|=.
4.D 以A为原点,AB,AD,AP所在直线为x轴、y轴、z轴建立如图所示的空间直角坐标系,则P(0,0,1),D(0,1,0),E,
所以=(0,1,-1),,
所以||=,||==-,
所以点E到直线PD的距离是.
故选D.
5.B 由题知,在正四面体APBC中,
因为AQ⊥平面PBC,
所以Q是△PBC的中心.
连接PQ,则),
所以×()
=)=.
故选B.
6.C 依题意,以A为坐标原点,分别以AB,AD,AP所在直线为x轴、y轴、z轴建立如图所示的空间直角坐标系,
因为AB=BC=2,AD=3,PA=2,
则P(0,0,2),B(2,0,0),C(2,2,0),D(0,3,0),
从而=(2,0,-2),=(2,2,-2),=(0,3,-2),
设平面PCD的法向量为n=(a,b,c),
则
不妨取c=3,则a=1,b=2,
所以平面PCD的一个法向量为n=(1,2,3),
设PB与平面PCD所成角为θ,
则sin θ=|cos<,n>|==.
7.C 以D为原点,DA,DC,DF所在直线为x轴、y轴、z轴建立如图所示的空间直角坐标系,
则D(0,0,0),A(2,0,0),C(0,4,0),E(2,4,1),C1(0,4,3),
∴=(-2,4,3),=(0,4,1).
设平面AEC1F的法向量为n=(x,y,z),
由
令z=1,则x=1,y=-,
所以n=.
又=(0,0,3),
∴点C到平面AEC1F的距离d=.
故选C.
8.B 由△PAD是以AD为斜边的等腰直角三角形,AB⊥平面PAD,底面ABCD为正方形,取AD的中点G,建立如图所示的空间直角坐标系,
则G(0,0,0),A(1,0,0),D(-1,0,0),B(1,2,0),P(0,0,1),设F(1,y,0),0
又=(1,0,-1),异面直线PA与EF成30°的角,
故=||||cos 30°,
即2=,
即(x-1)2=y2,0
∴||2=2(x-1)2∈(0,),
∴||∈(0,).
9.ABC 由题得,|a|=,故A正确;
设a=mb+nc,
即
解得
即a=3b+2c,所以向量a,b,c共面,故B正确;
因为a·b=3-4+1=0,
所以a⊥b,故C正确;
(a+b)·c=(4,0,2)·(-4,4,-1)=-18,故D错误.
故选ABC.
10.BD 因为
)=,故A不正确,B正确.
如图所示,过点D作DU⊥BC,过点U作VU⊥AB,UW⊥AC,
故向量在向量上的投影向量为,向量在向量上的投影向量为,
由题意易得,故,故C不正确,D正确.
故选BD.
11.ABD 如图所示,以BD的中点O为坐标原点,OD,OA,OC所在直线分别为x轴、y轴、z轴,建立空间直角坐标系Oxyz,
设正方形ABCD的边长为,
则D(1,0,0),B(-1,0,0),C(0,0,1),A(0,1,0),
所以=(0,-1,1),=(2,0,0),=0.
故AC⊥BD,A正确.
又||=,||=,||=,
所以△ACD为等边三角形,B正确.
对于C,为平面BCD的一个法向量,=(-1,-1,0),
cos<>==-=-.
因为直线与平面所成的角的范围是[0,],
所以AB与平面BCD所成的角为,故C错误.
又cos<>==-,
因为异面直线所成的角为锐角或直角,所以AB与CD所成的角为,故D正确.
12. 由题可得|a|==3,
∴向量a的单位向量的坐标为(2,2,-1)=.
13. 因为向量a与b的夹角为钝角,
所以a·b=-3-2(x-1)-3<0,
解得x>-2.
由题意得a与b不共线,则,
解得x≠,
所以x的取值范围是.
14. 建立空间直角坐标系如图所示,则A(1,0,0),F(1,1,0),C(0,0,1).
因为CM=BN=a(0
所以=0,a,a-1.
所以||=,
即MN的长为.
当a=时,||min=,即M,N分别为AC,BF的中点时,MN的长最小,最小值为.
15.解 (1)因为a∥b,易知y≠0,
所以,
解得x=2,y=-4,
则a=(2,4,1),b=(-2,-4,-1).
又b⊥c,所以b·c=0,
即-6+8-z=0,
解得z=2,于是c=(3,-2,2).
(2)由(1)得a+c=(5,2,3),b+c=(1,-6,1),
设向量a+c与b+c的夹角为θ,
因为cos θ==-,
所以向量a+c与b+c夹角的余弦值为-.
16.证明 ∵平面ADEF⊥平面ABCD,平面ADEF∩平面ABCD=AD,AD⊥ED,ED 平面ADEF,
∴ED⊥平面ABCD.
以D为原点,DA,DC,DE所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
则D(0,0,0),A(2,0,0),B(2,2,0),C(0,4,0),E(0,0,2),F(2,0,2).
(1)∵M为EC的中点,
∴M(0,2,1),
则=(-2,0,1),=(-2,0,0),=(0,0,2),
∴,故共面.
又BM 平面ADEF,
∴BM∥平面ADEF.
(2)=(-2,2,0),=(2,2,0),=(0,0,2),
∵=-4+4=0,∴BC⊥DB.
又=0,
∴BC⊥DE.
又DE∩DB=D,DE,DB 平面BDE,
∴BC⊥平面BDE.
17.(1)证明 以A为原点,AD,AA1,AB所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
则B(0,0,4),D(2,0,0),C(2,0,2),E(0,2,0),C1(2,4,2),B1(0,4,4),所以=(2,0,-2),=(2,2,2),
所以=2×2+0+2×(-2)=0,
所以,
即BC⊥EC1.
(2)解 因为=(0,4,0),=(-2,2,-2),
所以+λ=(2-2λ,2λ,-2-2λ).
设平面BB1M的法向量为n=(x,y,z),
所以
令x=1+λ,
则y=0,z=1-λ,得n=(1+λ,0,1-λ).
因为=(2,0,-2),
所以点C1到平面BB1M的距离d=,解得λ=.
18.解 (1)在题图1中作CH⊥AB,交AB于点H(图略),则BH=,
∴∠B=,∠D=,
AC=,
∴AC2+BC2=AB2,
∴BC⊥AC,
∴在题图2中,AC⊥BC.
又AD⊥BC,AD∩AC=A,AD,AC 平面ACD,
∴BC⊥平面ACD,
取AC中点F,连接DF,FE,则FA,FE,FD两两垂直,
以F为坐标原点,建立空间直角坐标系,如图,
D(0,0,),B(-,1,0),
∴线段BD的长为||=.
(2)=(,-1,),C(-,0,0),E(0,,0),=(,0,),=(,0),
设平面CDE的法向量为n=(x,y,z),
则取x=1,
得n=(1,-,-).
设直线BD与平面CDE所成的角为θ,
则直线BD与平面CDE所成的角的正弦值为
sin θ=.
19.(1)证明 因为CB=BD,2∠BCD=90°,故∠CBD=90°,
所以BC⊥BD.
又SD⊥BC,SD∩BD=D,SD,BD 平面SBD,
所以BC⊥平面SBD.
因为BC 平面SBC,
所以平面SBD⊥平面SBC.
(2)解 由(1)可得,平面ABCD⊥平面SBD,
设E为BD的中点,连接SE,
因为SB=SD=,
所以SE⊥BD,
故SE⊥平面ABCD.
如图,建立空间直角坐标系Axyz,则A(0,0,0),B(0,2,0),C(2,4,0),S(1,1,2).
因为=λ,
所以P(2-λ,4-3λ,2λ),
易得平面SBD的一个法向量为=(2,2,0).
设n=(x,y,z)为平面ABP的法向量,
=(0,2,0),=(2-λ,4-3λ,2λ),
由
不妨取n=(2λ,0,λ-2).
因为平面SBD与平面ABP的夹角为60°,
所以|cos<,n>|=,且λ>0,
解得λ=或λ=-2(舍去),
故λ的值为.
14
