小学数学北师大版四年级下册认识三角形和四边形作业(含解析)
文档属性
| 名称 | 小学数学北师大版四年级下册认识三角形和四边形作业(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 514.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-10 20:35:56 | ||
图片预览


文档简介
小学数学北师大版认识三角形和四边形作业
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下列三句话中正确的有( )个。
①在小数点的后面添上“0”或去掉“0”,小数的大小不变。
②大于2.6且小于2.8的小数只有一个。
③如果两个三角形能拼成一个平行四边形,那么它们一定完全相同。
A.1 B.2 C.3
2.甲、乙、丙三座通讯塔的位置构成一个三角形,已知甲与乙相距8千米,甲与丙相距5千米,那么乙和丙相距( )。
A.可能小于3千米 B.一定大于13千米
C.可能是15千米 D.可能是10千米
3.一个三角形中有一个内角是25°,它( )。
A.一定是锐角三角形 B.可能是等腰三角形
C.一定是直角三角形 D.一定是钝角三角形
4.下面几幅图中,不能判定三角形类型的是( )。
A. B. C.
5.两个图形有部分重叠(重叠部分涂色表示),( )个的重叠部分是梯形。
A.两个平行四边形 B.平行四边形与三角形
C.两个长方形 D.两个三角形
6.一个等腰三角形中,顶角是80°,它的一个底角是( )。
A.100 B.80° C.40° D.50°
7.如图,在方格纸上画了五个图形,其中是梯形的有( )。
A.①③⑤ B.①②④⑤ C.①③④⑤ D.①②③④⑤
8.如图,用两个完全一样的等腰梯形拼成一个平行四边形,每个梯形的周长是( )厘米。
A.35 B.50 C.55 D.70
9.等腰三角形是一种特殊的三角形,因为三角形中的两条边相等而得名。现在有一个等腰三角形,量得其中的两条边分别是3.45厘米和8.26厘米,那么另外一条边是( )厘米。
A.3.45 B.8.26
C.3.45或8.26都可以 D.3.45或8.26都不可以
10.如图,将图①折成图②,如果∠2+∠3=100°,那么∠4+∠5=( )°。
A.80 B.90 C.100 D.130
二、填空题
11.在三角形ABC中,∠A=65°,∠B=48°,则∠C=( )°,按角分,这是一个( )三角形。
12.用“正、长、平”分别代表正方形、长方形、平行四边形,填在如图的适当位置,正确表现三者之间的关系。
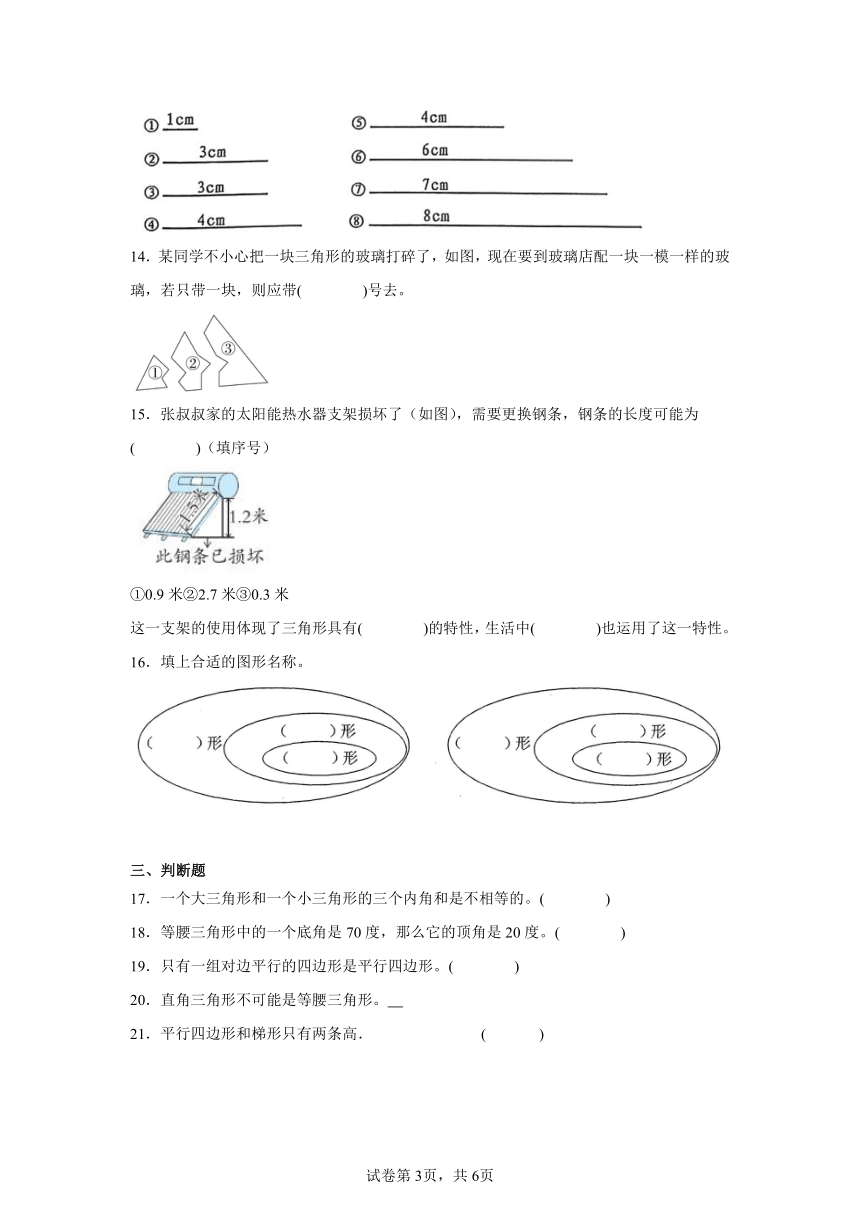
13.下面的线段中,能围成等腰三角形的3条线段有( )种选择方法,不能围成三角形的3条线段有( )种选择方法。能围成平行四边形的4条线段是( )。
14.某同学不小心把一块三角形的玻璃打碎了,如图,现在要到玻璃店配一块一模一样的玻璃,若只带一块,则应带( )号去。
15.张叔叔家的太阳能热水器支架损坏了(如图),需要更换钢条,钢条的长度可能为( )(填序号)
①0.9米②2.7米③0.3米
这一支架的使用体现了三角形具有( )的特性,生活中( )也运用了这一特性。
16.填上合适的图形名称。
三、判断题
17.一个大三角形和一个小三角形的三个内角和是不相等的。( )
18.等腰三角形中的一个底角是70度,那么它的顶角是20度。( )
19.只有一组对边平行的四边形是平行四边形。( )
20.直角三角形不可能是等腰三角形。
21.平行四边形和梯形只有两条高. ( )
四、计算题
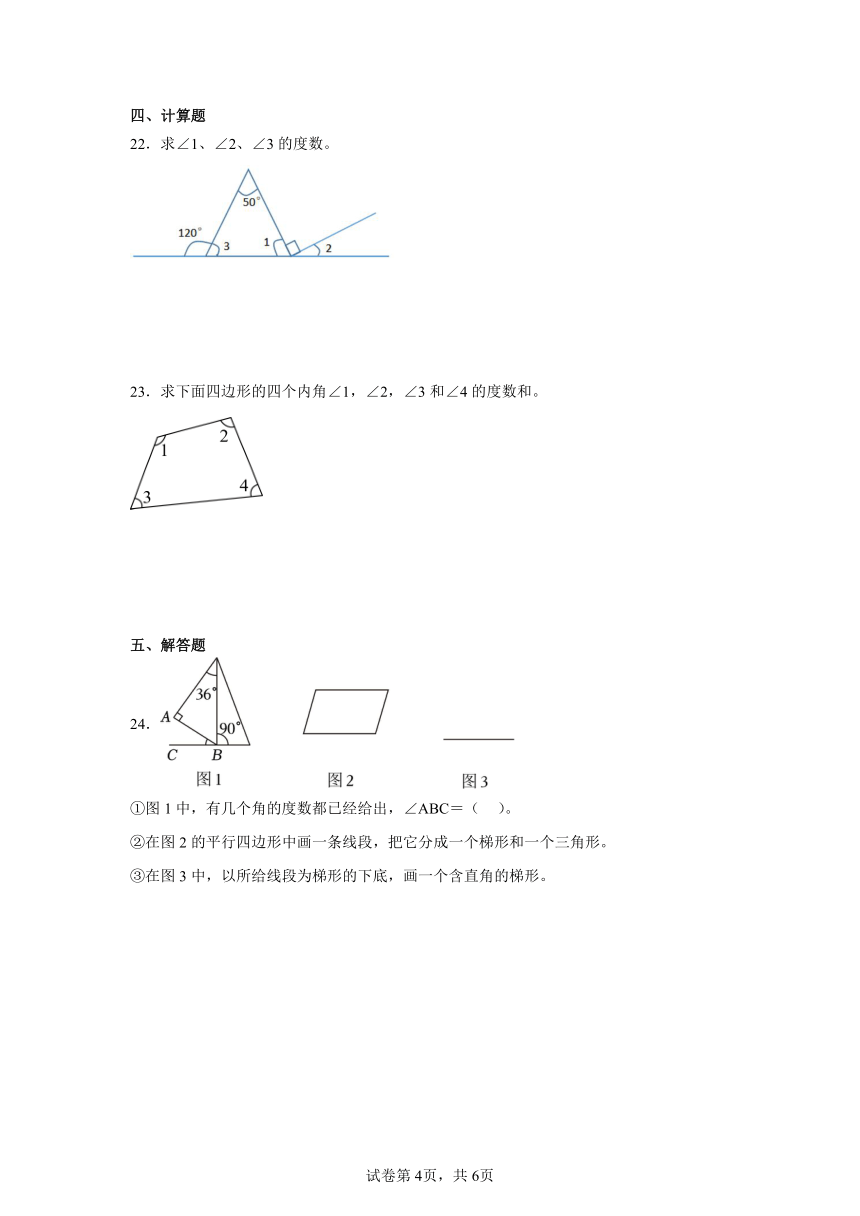
22.求∠1、∠2、∠3的度数。
23.求下面四边形的四个内角∠1,∠2,∠3和∠4的度数和。
五、解答题
24.
①图1中,有几个角的度数都已经给出,∠ABC=( )。
②在图2的平行四边形中画一条线段,把它分成一个梯形和一个三角形。
③在图3中,以所给线段为梯形的下底,画一个含直角的梯形。
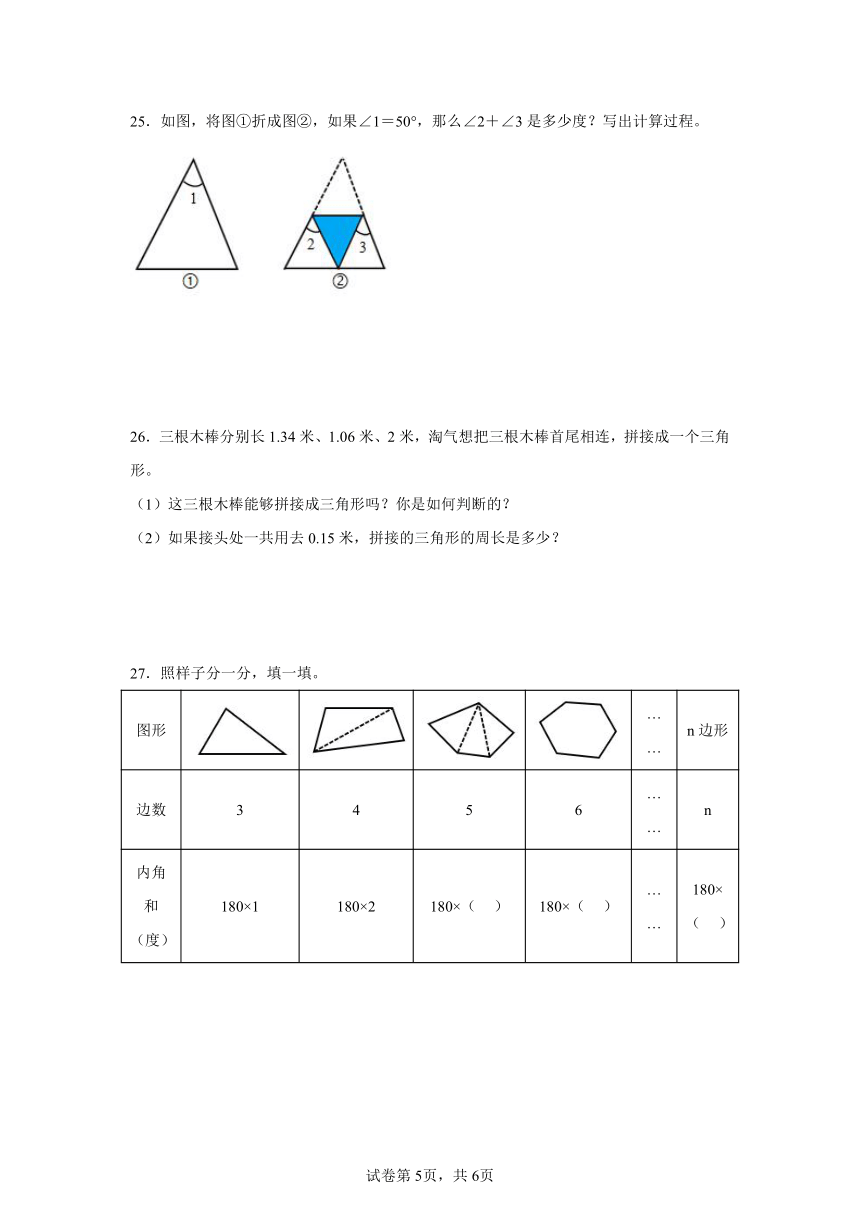
25.如图,将图①折成图②,如果∠1=50°,那么∠2+∠3是多少度?写出计算过程。
26.三根木棒分别长1.34米、1.06米、2米,淘气想把三根木棒首尾相连,拼接成一个三角形。
(1)这三根木棒能够拼接成三角形吗?你是如何判断的?
(2)如果接头处一共用去0.15米,拼接的三角形的周长是多少?
27.照样子分一分,填一填。
图形 …… n边形
边数 3 4 5 6 …… n
内角和(度) 180×1 180×2 180×( ) 180×( ) …… 180×( )
28.幸福村有一块梯形的土地(如下图),计划分出一块最大的正方形土地建造公园,使它为村民休闲娱乐的好场所,剩下的土地用来种植鲜花。
(1)请你根据题目中的要求先在图中,画一画,分一分。
(2)如果在用来种植鲜花的土地的一周围上篱笆,至少要准备多长的篱笆?
29.象棋是中国传统棋类益智游戏,在中国有着悠久的历史。下面是正在对弈的一盘象棋的情况。
(1)用数对表示下列棋子的位置。
( ),( ),( ),( ),( ),( )。
(2)根据象棋中“马”走“日”的规定,用“·”标出“马”下一步能走到的所有位置,并顺次连接这些点,得到的图形是( )边形。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】①根据小数的性质,在小数的末尾添上“0”或去掉“0”,小数的大小不变,但小数点后面的0不能随意修改;
②由题意可知要求大于2.6且小于2.8的小数,没有说明是几位小数,可以是一位小数、两位小数、三位小数……所以有无数个小数;
③两个完全一样的三角形可以拼成一个平行四边形;
【详解】①如:去掉2.06小数点后面的0变为2.6,此时2.6≠2.06,此时小数的大小已改变,选项说法错误;
②大于2.6且小于2.8的一位小数有2.7;大于2.6且小于2.8的两位小数有2.61、2.62、2.63、…;大于2.6且小于2.8的三位小数有2.611、2.621、2.631、…;…所以大于2.6且小于2.8的小数有无数个,选项说法不正确;
③如果两个三角形能拼成一个平行四边形,那么它们一定完全相同,选项说法正确;
故答案为:A
2.D
【分析】此题考查三角形的三边关系,即两边之和大于第三边,两边之差小于第三边;据此可解此题。
【详解】两边之和:8+5=13(千米)
两边之差:8-5=3(千米)
由此可知,乙和丙之间的距离大于3千米小于13千米。
A.可能小于3千米,不正确;
B.一定大于13千米,不正确;
C.可能是15千米,大于13千米,不正确;
D.可能是10千米,正确。
故答案为:D
3.B
【分析】当这个三角形中有一个内角是25°,假设它的另外两个角是25°和130°时,此时三角形是等腰三角形,也是钝角三角形;当这个三角形中有一个内角是25°,另外两个角是90°和65°时,三角形是直角三角形;当这个三角形中有一个内角是25°,假设它的另外两个角是85°和70°时,三角形是锐角三角形,据此作答。
【详解】根据上述分析可得:
一个三角形中有一个内角是25°,它可能是锐角三角形,等腰三角形,直角三角形或者是锐角三角形。
故答案为:B
4.C
【分析】根据三角形的分类,有一个角是钝角的三角形是钝角三角形,有一个角是直角的三角形是直角三角形,三个角都是锐角的三角形是锐角三角形。据此解答。
【详解】
A.露出的两个角都是锐角,且这两个锐角偏大,若把两边延长,就会出现第三个角,是一个锐角,这个三角形就是锐角三角形。
B.露出的角是一个直角,说明是一个直角三角形。
C.露出一个角是锐角,2个角的大小未知,因此不能判断三角形的种类。
故答案为:C
5.B
【分析】梯形是只有一组对边平行的四边形,平行四边形是两组对边分别平行的四边形,据此定义结合观察到的重叠图形特征进行判断即可。
【详解】
A.观察可知,由于平行四边形两组对边分别平行,故两个平行四边形重叠部分是一个平行四边形,不是梯形;
B.观察可知,由于平行四边形两组对边分别平行,平行四边形与三角形重叠部分是一个梯形;
C.观察可知,长方形是特殊的平行四边形,故两个长方形重叠部分是一个平行四边形,不是梯形;
D.观察可知,两个三角形重叠部分是一个四边形,不是梯形。
故答案为:B
6.D
【分析】等腰三角形的两个底角相等,根据三角形的内角和为180°可知,一个底角是(180°-80°)÷2。
【详解】(180°-80°)÷2
=100°÷2
=50°
它的一个底角是50°。
故答案为:D
7.C
【分析】两组对边分别平行且相等的四边形是平行四边形。只有一组对边平行的四边形是梯形。①是梯形,②是平行四边形,③是梯形,④是梯形,⑤是梯形。
【详解】其中是梯形的有①③④⑤。
故答案为:C
8.B
【分析】观察上图可知,等腰梯形的腰长为15厘米,梯形的上底加下底的和为20厘米,等腰梯形的周长=上底+下底+腰长×2,把数据代入计算即可解答。
【详解】20+15×2
=20+30
=50(厘米)
每个梯形的周长是50厘米。
故答案为:B
9.B
【分析】三角形的三边关系是:任意两边之和大于第三边,任意两边之差小于第三边,计算3.45与3.45的和,发现和比8.26小,那么两腰的长度不是3.45,两腰的长度是8.26,即第三条边的长度是8.26厘米。
【详解】3.45+3.45=6.9(厘米)
6.9<8.26
另外一条边是8.26厘米。
故答案为:B
10.C
【分析】将图①折成图②后,∠1与∠2和∠3组成了一个平角,1平角=180°,所以可得∠1=180°-(∠2+∠3),∠1、∠4和∠5是三角形的3个内角,三角形的内角和是180°,所以∠4+∠5=180°-∠1,据此解答即可。
【详解】∠1的度数是:
180°-(∠2+∠3)
=180°-100°
=80°
∠4+∠5=180°-∠1=180°-80°=100°
故答案为:C
11. 67 锐角
【分析】三角形内角和为180°,用180°减去∠A和∠B,即可求出∠C的度数;再根据最大角判断三角形的类型即可,若最大角>90°,则为钝角三角形,若最大角=90°,则为直角三角形,若最大角<90°,则为锐角三角形,据此解答。
【详解】根据上述分析可得:
180°-65°-48°
=115°-48°
=67°
90°>67°,这个三角形的最大角是个锐角。
所以在三角形ABC中,∠A=65°,∠B=48°,则∠C=67°,按角分,这是一个锐角三角形。
12.见详解
【分析】平行四边形是在同一个二维平面内,由两组平行线段组成的闭合图形。两组对边分别平行、四个角都是直角的四边形叫做长方形;长方形两组对边平行且相等,两条对角线相等且互相平分,长方形是特殊的平行四边形。四条边相等、四个角都是直角的四边形叫做正方形。正方形是特殊的长方形;据此可解此题。
【详解】
由分析可知:长方形是特殊的平行四边形,正方形是特殊的长方形;三者关系为:
13. 8 25 ②③④⑤
【分析】(1)要围成等腰三角形,那么三角形的三边中,就需要有两条线段的长度一样;即其中两条边是②和③或者④和⑤;再根据两边之和大于第三边以及两边之差小于第三边,来进行选择第三条边;能围成等腰三角形三条线段有:①②③、②③④、②③⑤、①④⑤、②④⑤、③④⑤、④⑤⑥、④⑤⑦;
(2)根据不满足两边之和大于第三边或两边之差小于第三边,不能围成三角形的3条线段有:①②④、①②⑤、①②⑥、①②⑦、①②⑧、①③④、①③⑤、①③⑥、①③⑦、①③⑧、①④⑥、①④⑦、①④⑧、①⑤⑥、①⑤⑦、①⑤⑧、①⑥⑦、①⑥⑧、①⑦⑧、②③⑥、②③⑦、②③⑧、③④⑦、③④⑧、④⑤⑧;据此可解此题;
(3)平行四边形对边平行且相等,要找出两组长度相等的线段为:②③④⑤;即可解此题。
【详解】根据分析:能围成等腰三角形的3条线段有8种搭配方法,不能围成三角形的3条线段有25种搭配方法。能围成平行四边形的4条线段是②③④⑤。
14.③
【分析】只要确定三角形的一条边和两个角,就能确定这个三角形的形状,据此即可解答。
【详解】①仅保留了原三角形的一个角和部分边,不能确定三角形的形状;②仅保留了原三角形的部分边,不能确定三角形的形状;③不但保留了原三角形的两个角还保留了其中一个边,可以确定三角形的形状,所以应该拿这块。
所以,应带③号去。
【点睛】本题主要考查学生对三角形知识的掌握和灵活运用。
15. ① 稳定性 自行车三角架
【分析】三角形的三边关系:两边之和大于第三条边,两边之差小于第三条边;
三角形具有稳定性,有着稳固、坚定、耐压的特点;平行四边形具有不稳定性,易变形。人们常利用三角形的稳定性,把自行车的支架做成三角形;
【详解】1.5+1.2=2.7(米),1.5-1.2=0.3(米),第三条边在0.3米和2.7米,只有0.9米符合要求。
张叔叔家的太阳能热水器支架损坏了(如上图),需要更换钢条,钢条的长度可能为①。
这一支架的使用体现了三角形具有稳定性的特性,生活中自行车三脚架也运用了这一特性。
【点睛】熟练掌握三角形的三边关系是解答此题的关键。
16.见详解
【分析】至少有2条边相等的三角形是等腰三角形,3条边相等的是等边三角形,等边三角形是特殊的等腰三角形;
有两组对边分别平行的四边形是平行四边形,正方形、长方形是特殊的平行四边形,正方形是特殊的长方形。
【详解】
【点睛】熟练掌握等腰三角形、等边三角形、平行四边形、长方形、正方形的特征是解答此题的关键。
17.×
【分析】三角形的内角和等于180度,据此即可解答。
【详解】根据分析可知,
一个大三角形和一个小三角形的三个内角和都等于180度,原说法错误。
故答案为:×
【点睛】本题主要考查学生对三角形内角和知识的掌握和灵活运用。
18.×
【分析】等腰三角形的特点是两个底角都相等,三角形的内角和是180°,依此判断即可。
【详解】假设等腰三角形中的一个底角是70°,顶角是20°;
70°+70°+20°=160°
故答案为:×
【点睛】熟记三角形的内角和度数是解答此题的关键。
19.×
【分析】只有一组对边平行的四边形是梯形,两组对边分别平行的四边形是梯形。
【详解】两组对边分别平行的四边形是平行四边形。
故答案为:×
【点睛】此题主要考查学生对梯形与平行四边形定义的掌握情况,根据定义直接解答。
20.×
【分析】三角形按角来分可分为锐角三角形、直角三角形和钝角三角形;按边来分可分为等腰三角形(含特殊情况等边三角形)和不等腰三角形。二者分类依据不同,直角三角形可能是等腰三角形。
【详解】在直角三角形中,当除直角外的另外两个角相等时,它们的对边也相等,也就是直角三角形也可以是等腰三角形,所以上面说法是错误的。
【点睛】此题考查了三角形的分类,按边分类和按角分类区分。
21.×
【详解】平行四边形的高是指对边之间的距离,那么,两组对边之间都可以画无数条垂直线段,所以,有无数条高.
22.∠1=70°
∠2=20°
∠3=60°
【分析】根据题图可知,∠3和120°的角组成一个平角,则∠3=180°-120°=60°。根据三角形的内角和为180°可知,∠1=180°-50°-∠3=70°。∠1、∠2和一个直角组成一个平角,则∠2=180°-90°-∠1=20°。
【详解】∠3=180°-120°=60°
∠1=180°-50°-∠3=180°-50°-60°=70°
∠2=180°-90°-∠1=180°-90°-70°=20°
23.360°
【分析】三角形的内角和是180°。如下图,四边形可以分成两个三角形。所以题图中的四边形四个内角的度数和是三角形内角和的2倍。
【详解】180°×2=360°
答:四边形的四个内角∠1,∠2,∠3和∠4的度数和为360°。
24.①36度
②③见详解
【分析】(1)图1中已知直角三角形中一个角为36度一个角为直角,根据三角形的内角和为180度,据此求出第三个角的度数;然后根据平角为180度,用平角减去90度再减去上述求出的第三个角的度数,即可求出∠ABC的度数。
(2)要将平行四边形分成一个梯形和一个三角形;过平行四边形的任意一个顶点,做一条线段,相交于与这个顶点不相邻的任意一条边即可将平行四边形分成把它分成一个梯形和一个三角形。
(3)只有一组对边平行的四边形叫做梯形,一腰垂直于底的梯形叫直角梯形。据此可知,先过已知线段的一个端点,做一条垂直于底的腰,再过腰的另一个顶点,做一条平行于下底的线段为上底,上底长度不等于下底,然后再连接上底的另一个端点和下底的另一个端点,即可画成一个直角梯形。
【详解】根据分析:
①180-90-(180-36-90)
=180-90-180+36+90
=36(度)
由此可知,∠ABC=36度。
②如下图所示:
③如下图所示:
25.100°
【分析】如下图所示:
根据折叠可知,∠4=∠5,∠6=∠7,∠5+∠7=180°-50°=130°,所以∠4+∠5+∠6+∠7=130°×2=260°。因为∠2+∠4+∠5=180°,∠3+∠6+∠7=180°,所以∠2+∠3=180°+180°-260°=100°。
【详解】(180°-50°)×2
=130°×2
=260°
∠2+∠3=180°+180°-260°=100°
答:∠2+∠3是100度。
【点睛】本题考查三角形内角度数的计算,三角形的内角和是180°。
26.(1)能;理由见详解
(2)4.25米
【分析】(1)三角形的三边关系:两边之和一定大于第三条边,据此解答。
(2)用这三根木棒的长度之和减去0.15,求出拼接的三角形的周长是多少。
【详解】(1)1.34+1.06=2.40(米)
2.40米>2米
答:这三根木棒能够拼接成三角形。
(2)1.34+1.06+2-0.15
=2.40+2-0.15
=4.40-0.15
=4.25(米)
答:拼接的三角形的周长是4.25米。
【点睛】本题考查了小数的加、减法计算及应用,计算时,小数点一定要对齐,再相加、减。
27.见详解
【分析】从图中可知:能把五边形分成3个三角形,那么五边形的内角和=180×3(度);先把六边形分成4个三角形,那么六边形的内角和=180×4(度);观察图形可知,n边形能分成的三角形的个数是(n-2)个,那么n边形的内角和是180×(n-2)度。
【详解】
图形 …… n边形
边数 3 4 5 6 …… n
内角和(度) 180×1 180×2 180×( 3 ) 180×( 4 ) …… 180×( n-2 )
【点睛】本题主要考查了多边形的内角和知识,解题的关键是先把多边形分成三角形,再根据三角形的内角和解答。
28.(1)见详解
(2)120米
【分析】(1)根据题目,图示是直角梯形,要划分出一块最大的正方形土地,那么正方形应该贴合直角梯形直角边的腰(高),也就是正方形的边长应该等于梯形的高,即40m。又梯形的上底长为40米,故实际就是从上底右边端点作一根垂线段垂直于下底,据此画出图即可。
(2)根据(1)的示意图可知剩下的土地是一个三角形,要围的篱笆长就是求其周长,将三边长相加即可得到要围的篱笆长。
【详解】(1)如图所示,左边的正方形是最大的正方形,用于建造公园,右边三角形用于种植鲜花。
(2)根据(1)的示意图可知剩下的土地是一个三角形,其中斜边长度为50米,两条直角边的长度分别为40米和(70-40)米,则要围的篱笆长=50+40+(70-40)=50+40+30=120(米)。
答:至少要准备120米的篱笆。
29.(1)将(0,4);象(2,4);兵(3,2);炮(1,3);车(7,1);士(8,4)
(2)见详解;八
【分析】(1)用数对表示位置,数对的前一个数表示第几列,后一个数表示第几行,据此可得出棋子对应位置;
(2)象棋中“马”走“日”的规定,经过两个方格的对角点处是下一步要走的位置,再将这几点连接起来得出答案。
【详解】(1)用数对表示为:将在第0列第4行即(0,4);象在第2列第4行即(2,4);兵在第3列第2行即(3,2);炮在第1列第3行即(1,3);车在第7列第1行即(7,1);士在第8列第4行即(8,4)。
(2)画出点表示如图:
这八个点依次连接组成八边形。
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下列三句话中正确的有( )个。
①在小数点的后面添上“0”或去掉“0”,小数的大小不变。
②大于2.6且小于2.8的小数只有一个。
③如果两个三角形能拼成一个平行四边形,那么它们一定完全相同。
A.1 B.2 C.3
2.甲、乙、丙三座通讯塔的位置构成一个三角形,已知甲与乙相距8千米,甲与丙相距5千米,那么乙和丙相距( )。
A.可能小于3千米 B.一定大于13千米
C.可能是15千米 D.可能是10千米
3.一个三角形中有一个内角是25°,它( )。
A.一定是锐角三角形 B.可能是等腰三角形
C.一定是直角三角形 D.一定是钝角三角形
4.下面几幅图中,不能判定三角形类型的是( )。
A. B. C.
5.两个图形有部分重叠(重叠部分涂色表示),( )个的重叠部分是梯形。
A.两个平行四边形 B.平行四边形与三角形
C.两个长方形 D.两个三角形
6.一个等腰三角形中,顶角是80°,它的一个底角是( )。
A.100 B.80° C.40° D.50°
7.如图,在方格纸上画了五个图形,其中是梯形的有( )。
A.①③⑤ B.①②④⑤ C.①③④⑤ D.①②③④⑤
8.如图,用两个完全一样的等腰梯形拼成一个平行四边形,每个梯形的周长是( )厘米。
A.35 B.50 C.55 D.70
9.等腰三角形是一种特殊的三角形,因为三角形中的两条边相等而得名。现在有一个等腰三角形,量得其中的两条边分别是3.45厘米和8.26厘米,那么另外一条边是( )厘米。
A.3.45 B.8.26
C.3.45或8.26都可以 D.3.45或8.26都不可以
10.如图,将图①折成图②,如果∠2+∠3=100°,那么∠4+∠5=( )°。
A.80 B.90 C.100 D.130
二、填空题
11.在三角形ABC中,∠A=65°,∠B=48°,则∠C=( )°,按角分,这是一个( )三角形。
12.用“正、长、平”分别代表正方形、长方形、平行四边形,填在如图的适当位置,正确表现三者之间的关系。
13.下面的线段中,能围成等腰三角形的3条线段有( )种选择方法,不能围成三角形的3条线段有( )种选择方法。能围成平行四边形的4条线段是( )。
14.某同学不小心把一块三角形的玻璃打碎了,如图,现在要到玻璃店配一块一模一样的玻璃,若只带一块,则应带( )号去。
15.张叔叔家的太阳能热水器支架损坏了(如图),需要更换钢条,钢条的长度可能为( )(填序号)
①0.9米②2.7米③0.3米
这一支架的使用体现了三角形具有( )的特性,生活中( )也运用了这一特性。
16.填上合适的图形名称。
三、判断题
17.一个大三角形和一个小三角形的三个内角和是不相等的。( )
18.等腰三角形中的一个底角是70度,那么它的顶角是20度。( )
19.只有一组对边平行的四边形是平行四边形。( )
20.直角三角形不可能是等腰三角形。
21.平行四边形和梯形只有两条高. ( )
四、计算题
22.求∠1、∠2、∠3的度数。
23.求下面四边形的四个内角∠1,∠2,∠3和∠4的度数和。
五、解答题
24.
①图1中,有几个角的度数都已经给出,∠ABC=( )。
②在图2的平行四边形中画一条线段,把它分成一个梯形和一个三角形。
③在图3中,以所给线段为梯形的下底,画一个含直角的梯形。
25.如图,将图①折成图②,如果∠1=50°,那么∠2+∠3是多少度?写出计算过程。
26.三根木棒分别长1.34米、1.06米、2米,淘气想把三根木棒首尾相连,拼接成一个三角形。
(1)这三根木棒能够拼接成三角形吗?你是如何判断的?
(2)如果接头处一共用去0.15米,拼接的三角形的周长是多少?
27.照样子分一分,填一填。
图形 …… n边形
边数 3 4 5 6 …… n
内角和(度) 180×1 180×2 180×( ) 180×( ) …… 180×( )
28.幸福村有一块梯形的土地(如下图),计划分出一块最大的正方形土地建造公园,使它为村民休闲娱乐的好场所,剩下的土地用来种植鲜花。
(1)请你根据题目中的要求先在图中,画一画,分一分。
(2)如果在用来种植鲜花的土地的一周围上篱笆,至少要准备多长的篱笆?
29.象棋是中国传统棋类益智游戏,在中国有着悠久的历史。下面是正在对弈的一盘象棋的情况。
(1)用数对表示下列棋子的位置。
( ),( ),( ),( ),( ),( )。
(2)根据象棋中“马”走“日”的规定,用“·”标出“马”下一步能走到的所有位置,并顺次连接这些点,得到的图形是( )边形。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】①根据小数的性质,在小数的末尾添上“0”或去掉“0”,小数的大小不变,但小数点后面的0不能随意修改;
②由题意可知要求大于2.6且小于2.8的小数,没有说明是几位小数,可以是一位小数、两位小数、三位小数……所以有无数个小数;
③两个完全一样的三角形可以拼成一个平行四边形;
【详解】①如:去掉2.06小数点后面的0变为2.6,此时2.6≠2.06,此时小数的大小已改变,选项说法错误;
②大于2.6且小于2.8的一位小数有2.7;大于2.6且小于2.8的两位小数有2.61、2.62、2.63、…;大于2.6且小于2.8的三位小数有2.611、2.621、2.631、…;…所以大于2.6且小于2.8的小数有无数个,选项说法不正确;
③如果两个三角形能拼成一个平行四边形,那么它们一定完全相同,选项说法正确;
故答案为:A
2.D
【分析】此题考查三角形的三边关系,即两边之和大于第三边,两边之差小于第三边;据此可解此题。
【详解】两边之和:8+5=13(千米)
两边之差:8-5=3(千米)
由此可知,乙和丙之间的距离大于3千米小于13千米。
A.可能小于3千米,不正确;
B.一定大于13千米,不正确;
C.可能是15千米,大于13千米,不正确;
D.可能是10千米,正确。
故答案为:D
3.B
【分析】当这个三角形中有一个内角是25°,假设它的另外两个角是25°和130°时,此时三角形是等腰三角形,也是钝角三角形;当这个三角形中有一个内角是25°,另外两个角是90°和65°时,三角形是直角三角形;当这个三角形中有一个内角是25°,假设它的另外两个角是85°和70°时,三角形是锐角三角形,据此作答。
【详解】根据上述分析可得:
一个三角形中有一个内角是25°,它可能是锐角三角形,等腰三角形,直角三角形或者是锐角三角形。
故答案为:B
4.C
【分析】根据三角形的分类,有一个角是钝角的三角形是钝角三角形,有一个角是直角的三角形是直角三角形,三个角都是锐角的三角形是锐角三角形。据此解答。
【详解】
A.露出的两个角都是锐角,且这两个锐角偏大,若把两边延长,就会出现第三个角,是一个锐角,这个三角形就是锐角三角形。
B.露出的角是一个直角,说明是一个直角三角形。
C.露出一个角是锐角,2个角的大小未知,因此不能判断三角形的种类。
故答案为:C
5.B
【分析】梯形是只有一组对边平行的四边形,平行四边形是两组对边分别平行的四边形,据此定义结合观察到的重叠图形特征进行判断即可。
【详解】
A.观察可知,由于平行四边形两组对边分别平行,故两个平行四边形重叠部分是一个平行四边形,不是梯形;
B.观察可知,由于平行四边形两组对边分别平行,平行四边形与三角形重叠部分是一个梯形;
C.观察可知,长方形是特殊的平行四边形,故两个长方形重叠部分是一个平行四边形,不是梯形;
D.观察可知,两个三角形重叠部分是一个四边形,不是梯形。
故答案为:B
6.D
【分析】等腰三角形的两个底角相等,根据三角形的内角和为180°可知,一个底角是(180°-80°)÷2。
【详解】(180°-80°)÷2
=100°÷2
=50°
它的一个底角是50°。
故答案为:D
7.C
【分析】两组对边分别平行且相等的四边形是平行四边形。只有一组对边平行的四边形是梯形。①是梯形,②是平行四边形,③是梯形,④是梯形,⑤是梯形。
【详解】其中是梯形的有①③④⑤。
故答案为:C
8.B
【分析】观察上图可知,等腰梯形的腰长为15厘米,梯形的上底加下底的和为20厘米,等腰梯形的周长=上底+下底+腰长×2,把数据代入计算即可解答。
【详解】20+15×2
=20+30
=50(厘米)
每个梯形的周长是50厘米。
故答案为:B
9.B
【分析】三角形的三边关系是:任意两边之和大于第三边,任意两边之差小于第三边,计算3.45与3.45的和,发现和比8.26小,那么两腰的长度不是3.45,两腰的长度是8.26,即第三条边的长度是8.26厘米。
【详解】3.45+3.45=6.9(厘米)
6.9<8.26
另外一条边是8.26厘米。
故答案为:B
10.C
【分析】将图①折成图②后,∠1与∠2和∠3组成了一个平角,1平角=180°,所以可得∠1=180°-(∠2+∠3),∠1、∠4和∠5是三角形的3个内角,三角形的内角和是180°,所以∠4+∠5=180°-∠1,据此解答即可。
【详解】∠1的度数是:
180°-(∠2+∠3)
=180°-100°
=80°
∠4+∠5=180°-∠1=180°-80°=100°
故答案为:C
11. 67 锐角
【分析】三角形内角和为180°,用180°减去∠A和∠B,即可求出∠C的度数;再根据最大角判断三角形的类型即可,若最大角>90°,则为钝角三角形,若最大角=90°,则为直角三角形,若最大角<90°,则为锐角三角形,据此解答。
【详解】根据上述分析可得:
180°-65°-48°
=115°-48°
=67°
90°>67°,这个三角形的最大角是个锐角。
所以在三角形ABC中,∠A=65°,∠B=48°,则∠C=67°,按角分,这是一个锐角三角形。
12.见详解
【分析】平行四边形是在同一个二维平面内,由两组平行线段组成的闭合图形。两组对边分别平行、四个角都是直角的四边形叫做长方形;长方形两组对边平行且相等,两条对角线相等且互相平分,长方形是特殊的平行四边形。四条边相等、四个角都是直角的四边形叫做正方形。正方形是特殊的长方形;据此可解此题。
【详解】
由分析可知:长方形是特殊的平行四边形,正方形是特殊的长方形;三者关系为:
13. 8 25 ②③④⑤
【分析】(1)要围成等腰三角形,那么三角形的三边中,就需要有两条线段的长度一样;即其中两条边是②和③或者④和⑤;再根据两边之和大于第三边以及两边之差小于第三边,来进行选择第三条边;能围成等腰三角形三条线段有:①②③、②③④、②③⑤、①④⑤、②④⑤、③④⑤、④⑤⑥、④⑤⑦;
(2)根据不满足两边之和大于第三边或两边之差小于第三边,不能围成三角形的3条线段有:①②④、①②⑤、①②⑥、①②⑦、①②⑧、①③④、①③⑤、①③⑥、①③⑦、①③⑧、①④⑥、①④⑦、①④⑧、①⑤⑥、①⑤⑦、①⑤⑧、①⑥⑦、①⑥⑧、①⑦⑧、②③⑥、②③⑦、②③⑧、③④⑦、③④⑧、④⑤⑧;据此可解此题;
(3)平行四边形对边平行且相等,要找出两组长度相等的线段为:②③④⑤;即可解此题。
【详解】根据分析:能围成等腰三角形的3条线段有8种搭配方法,不能围成三角形的3条线段有25种搭配方法。能围成平行四边形的4条线段是②③④⑤。
14.③
【分析】只要确定三角形的一条边和两个角,就能确定这个三角形的形状,据此即可解答。
【详解】①仅保留了原三角形的一个角和部分边,不能确定三角形的形状;②仅保留了原三角形的部分边,不能确定三角形的形状;③不但保留了原三角形的两个角还保留了其中一个边,可以确定三角形的形状,所以应该拿这块。
所以,应带③号去。
【点睛】本题主要考查学生对三角形知识的掌握和灵活运用。
15. ① 稳定性 自行车三角架
【分析】三角形的三边关系:两边之和大于第三条边,两边之差小于第三条边;
三角形具有稳定性,有着稳固、坚定、耐压的特点;平行四边形具有不稳定性,易变形。人们常利用三角形的稳定性,把自行车的支架做成三角形;
【详解】1.5+1.2=2.7(米),1.5-1.2=0.3(米),第三条边在0.3米和2.7米,只有0.9米符合要求。
张叔叔家的太阳能热水器支架损坏了(如上图),需要更换钢条,钢条的长度可能为①。
这一支架的使用体现了三角形具有稳定性的特性,生活中自行车三脚架也运用了这一特性。
【点睛】熟练掌握三角形的三边关系是解答此题的关键。
16.见详解
【分析】至少有2条边相等的三角形是等腰三角形,3条边相等的是等边三角形,等边三角形是特殊的等腰三角形;
有两组对边分别平行的四边形是平行四边形,正方形、长方形是特殊的平行四边形,正方形是特殊的长方形。
【详解】
【点睛】熟练掌握等腰三角形、等边三角形、平行四边形、长方形、正方形的特征是解答此题的关键。
17.×
【分析】三角形的内角和等于180度,据此即可解答。
【详解】根据分析可知,
一个大三角形和一个小三角形的三个内角和都等于180度,原说法错误。
故答案为:×
【点睛】本题主要考查学生对三角形内角和知识的掌握和灵活运用。
18.×
【分析】等腰三角形的特点是两个底角都相等,三角形的内角和是180°,依此判断即可。
【详解】假设等腰三角形中的一个底角是70°,顶角是20°;
70°+70°+20°=160°
故答案为:×
【点睛】熟记三角形的内角和度数是解答此题的关键。
19.×
【分析】只有一组对边平行的四边形是梯形,两组对边分别平行的四边形是梯形。
【详解】两组对边分别平行的四边形是平行四边形。
故答案为:×
【点睛】此题主要考查学生对梯形与平行四边形定义的掌握情况,根据定义直接解答。
20.×
【分析】三角形按角来分可分为锐角三角形、直角三角形和钝角三角形;按边来分可分为等腰三角形(含特殊情况等边三角形)和不等腰三角形。二者分类依据不同,直角三角形可能是等腰三角形。
【详解】在直角三角形中,当除直角外的另外两个角相等时,它们的对边也相等,也就是直角三角形也可以是等腰三角形,所以上面说法是错误的。
【点睛】此题考查了三角形的分类,按边分类和按角分类区分。
21.×
【详解】平行四边形的高是指对边之间的距离,那么,两组对边之间都可以画无数条垂直线段,所以,有无数条高.
22.∠1=70°
∠2=20°
∠3=60°
【分析】根据题图可知,∠3和120°的角组成一个平角,则∠3=180°-120°=60°。根据三角形的内角和为180°可知,∠1=180°-50°-∠3=70°。∠1、∠2和一个直角组成一个平角,则∠2=180°-90°-∠1=20°。
【详解】∠3=180°-120°=60°
∠1=180°-50°-∠3=180°-50°-60°=70°
∠2=180°-90°-∠1=180°-90°-70°=20°
23.360°
【分析】三角形的内角和是180°。如下图,四边形可以分成两个三角形。所以题图中的四边形四个内角的度数和是三角形内角和的2倍。
【详解】180°×2=360°
答:四边形的四个内角∠1,∠2,∠3和∠4的度数和为360°。
24.①36度
②③见详解
【分析】(1)图1中已知直角三角形中一个角为36度一个角为直角,根据三角形的内角和为180度,据此求出第三个角的度数;然后根据平角为180度,用平角减去90度再减去上述求出的第三个角的度数,即可求出∠ABC的度数。
(2)要将平行四边形分成一个梯形和一个三角形;过平行四边形的任意一个顶点,做一条线段,相交于与这个顶点不相邻的任意一条边即可将平行四边形分成把它分成一个梯形和一个三角形。
(3)只有一组对边平行的四边形叫做梯形,一腰垂直于底的梯形叫直角梯形。据此可知,先过已知线段的一个端点,做一条垂直于底的腰,再过腰的另一个顶点,做一条平行于下底的线段为上底,上底长度不等于下底,然后再连接上底的另一个端点和下底的另一个端点,即可画成一个直角梯形。
【详解】根据分析:
①180-90-(180-36-90)
=180-90-180+36+90
=36(度)
由此可知,∠ABC=36度。
②如下图所示:
③如下图所示:
25.100°
【分析】如下图所示:
根据折叠可知,∠4=∠5,∠6=∠7,∠5+∠7=180°-50°=130°,所以∠4+∠5+∠6+∠7=130°×2=260°。因为∠2+∠4+∠5=180°,∠3+∠6+∠7=180°,所以∠2+∠3=180°+180°-260°=100°。
【详解】(180°-50°)×2
=130°×2
=260°
∠2+∠3=180°+180°-260°=100°
答:∠2+∠3是100度。
【点睛】本题考查三角形内角度数的计算,三角形的内角和是180°。
26.(1)能;理由见详解
(2)4.25米
【分析】(1)三角形的三边关系:两边之和一定大于第三条边,据此解答。
(2)用这三根木棒的长度之和减去0.15,求出拼接的三角形的周长是多少。
【详解】(1)1.34+1.06=2.40(米)
2.40米>2米
答:这三根木棒能够拼接成三角形。
(2)1.34+1.06+2-0.15
=2.40+2-0.15
=4.40-0.15
=4.25(米)
答:拼接的三角形的周长是4.25米。
【点睛】本题考查了小数的加、减法计算及应用,计算时,小数点一定要对齐,再相加、减。
27.见详解
【分析】从图中可知:能把五边形分成3个三角形,那么五边形的内角和=180×3(度);先把六边形分成4个三角形,那么六边形的内角和=180×4(度);观察图形可知,n边形能分成的三角形的个数是(n-2)个,那么n边形的内角和是180×(n-2)度。
【详解】
图形 …… n边形
边数 3 4 5 6 …… n
内角和(度) 180×1 180×2 180×( 3 ) 180×( 4 ) …… 180×( n-2 )
【点睛】本题主要考查了多边形的内角和知识,解题的关键是先把多边形分成三角形,再根据三角形的内角和解答。
28.(1)见详解
(2)120米
【分析】(1)根据题目,图示是直角梯形,要划分出一块最大的正方形土地,那么正方形应该贴合直角梯形直角边的腰(高),也就是正方形的边长应该等于梯形的高,即40m。又梯形的上底长为40米,故实际就是从上底右边端点作一根垂线段垂直于下底,据此画出图即可。
(2)根据(1)的示意图可知剩下的土地是一个三角形,要围的篱笆长就是求其周长,将三边长相加即可得到要围的篱笆长。
【详解】(1)如图所示,左边的正方形是最大的正方形,用于建造公园,右边三角形用于种植鲜花。
(2)根据(1)的示意图可知剩下的土地是一个三角形,其中斜边长度为50米,两条直角边的长度分别为40米和(70-40)米,则要围的篱笆长=50+40+(70-40)=50+40+30=120(米)。
答:至少要准备120米的篱笆。
29.(1)将(0,4);象(2,4);兵(3,2);炮(1,3);车(7,1);士(8,4)
(2)见详解;八
【分析】(1)用数对表示位置,数对的前一个数表示第几列,后一个数表示第几行,据此可得出棋子对应位置;
(2)象棋中“马”走“日”的规定,经过两个方格的对角点处是下一步要走的位置,再将这几点连接起来得出答案。
【详解】(1)用数对表示为:将在第0列第4行即(0,4);象在第2列第4行即(2,4);兵在第3列第2行即(3,2);炮在第1列第3行即(1,3);车在第7列第1行即(7,1);士在第8列第4行即(8,4)。
(2)画出点表示如图:
这八个点依次连接组成八边形。
答案第1页,共2页
答案第1页,共2页
