辽宁省沈阳市期末模拟测试卷(试题)2023-2024学年数学六年级下册北师大版(含答案)
文档属性
| 名称 | 辽宁省沈阳市期末模拟测试卷(试题)2023-2024学年数学六年级下册北师大版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 447.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-11 08:25:17 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
辽宁省沈阳市期末模拟测试卷(试题)2023-2024学年数学六年级下册北师大版
一、选择题
1.在一个比例中,已知两个外项互为倒数,其中一个内项是最小的合数,另一个内项是( )。
A.4 B.0.5 C.2 D.0.25
2.A÷2=B×5,A和B的最简整数比是( )。(A和B都不为0)
A.5∶1 B.2∶5 C.5∶2 D.10∶1
3.下图是六(1)班的教室平面图,亮亮在平面图上量得教室的长为5cm,这间教室的实际长是10m,这幅平面图的比例尺是( )。
A.1∶2 B.2∶1 C.1∶200 D.200∶1
4.甲乙两轮均为圆形,甲轮滚动2周的距离,乙轮要滚动3周,甲轮半径与乙轮半径的比是( )。
A.4∶9 B.9∶4 C.2∶3 D.3∶2
5.等底等高的圆柱、正方体、长方体的体积相比,( )。
A.长方体最大 B.正方体最大 C.一样大 D.圆柱最大
6.体育课上,老师喊的口令是“向后转”,你的身体应该( )。
A.顺时针旋转90° B.逆时针旋转90°
C.顺时针旋转180° D.逆时针旋转180°
二、填空题
7.同一时间、同一地点,树高和它的影子长成( )比例关系。
8.工人叔叔要包一批书,如果每包20本,要捆18包。如果每包30本,要捆( )包。
9.在比例尺为1∶4000000的地图上,量得A,B两地的距离是3厘米,A、B两地的实际距离是( )千米。
10.如图,将一个高10厘米、底面半径5厘米的圆柱平均分成32份,拼成一个近似的长方体,长方体的体积是( )立方厘米,表面积比原来增加了( )平方分米。
11.一个圆柱和圆锥等底等高,它们的体积和是80cm3,那么圆柱的体积是( )cm3,圆锥的体积是( )cm3。
12.如图,把一个棱长是6分米的正方体木料削成一个最大的圆柱,圆柱的体积是( )立方分米;再将圆柱削成一个最大的圆锥,还要再削去( )立方分米。
三、判断题
13.2018年第一季度有90天. ( )
14.一个圆锥的体积是6立方厘米,那么圆柱的体积是18立方厘米。( )
15.工作总量一定,已完成的部分与未完成的部分成反比例. ( )
16.体积相等的圆柱,它们的表面积也相等。( )
17.某校平面图的比例尺为米。 ( )
四、计算题
18.直接写得数.
×= ÷= 1-= 0.13= (+)×8=
-= += ×= 0÷= ÷3×÷3=
19.计算(能简算的要简算)
90÷÷50%
25×1.6×12.5
20.解方程。
45%x=36 13x-8x=25 6∶0.5=x∶
21.计算下面图形的体积。(单位:立方厘米)
五、解答题
22.配制一种农药,药粉和水的质量比是1∶500,现有水5000千克,配制这种农药需要药粉多少千克?(用比例解)
23.在比例尺是1∶7500000的地图上,量得甲、乙两地相距12厘米,一辆汽车以每小时60千米的速度从甲地开往乙地,需要多少小时能走完全程?
24.一个圆锥体铁块,底面半径是5厘米,高是3厘米,将这个圆锥体铁块放入到装有水的圆柱形容器中,完全浸没且没有水溢出,已知圆柱从里面量直径是20厘米,铁块放入后水面会上升多少厘米?
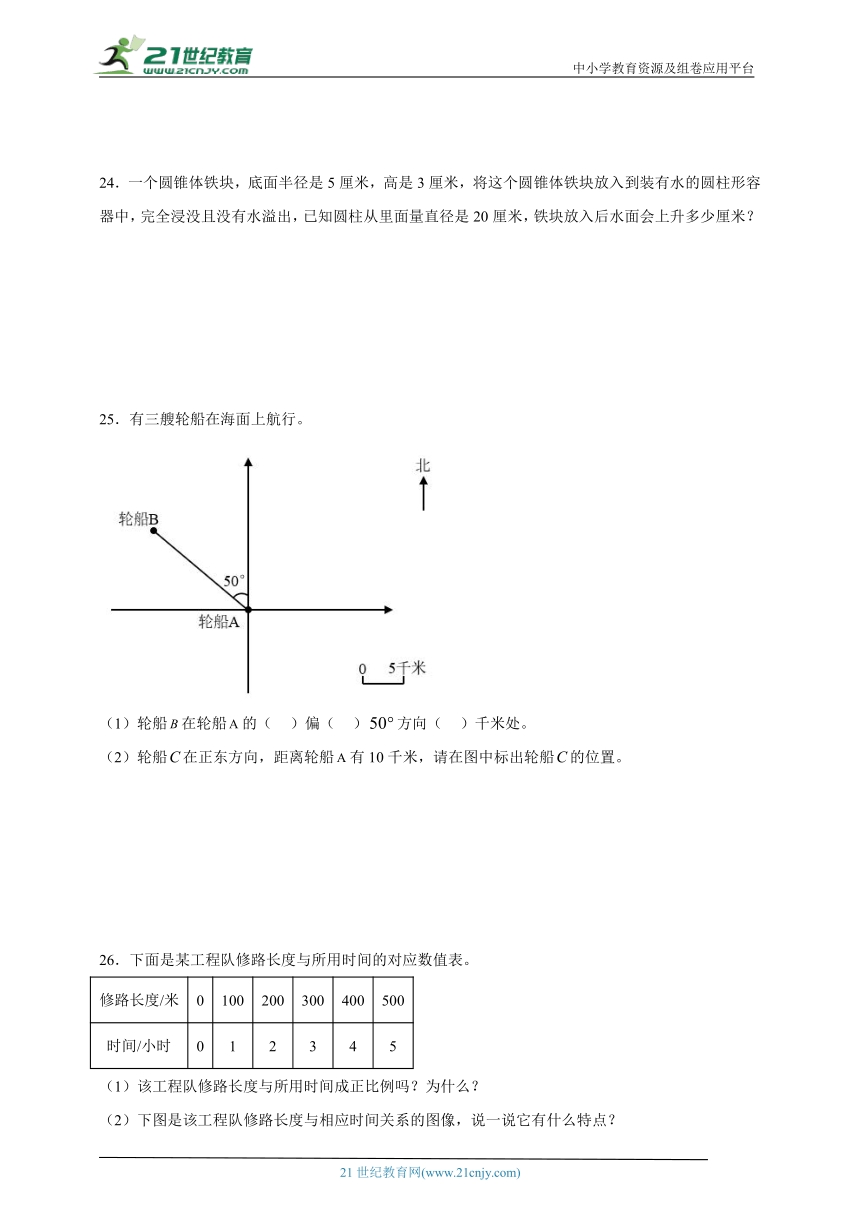
25.有三艘轮船在海面上航行。
(1)轮船在轮船的( )偏( )方向( )千米处。
(2)轮船在正东方向,距离轮船有10千米,请在图中标出轮船的位置。
26.下面是某工程队修路长度与所用时间的对应数值表。
修路长度/米 0 100 200 300 400 500
时间/小时 0 1 2 3 4 5
(1)该工程队修路长度与所用时间成正比例吗?为什么?
(2)下图是该工程队修路长度与相应时间关系的图像,说一说它有什么特点?
(3)照这样计算,该工程队9小时修路多少米?
参考答案:
1.D
【分析】根据比例的基本性质:两个外项之积等于两个内项之积;倒数的意义:乘积是1的两个数互为倒数;最小的合数是4;根据题意,两个外项互为倒数,即两个外项之积等于1,两个内项之积也等于1;其中一个内项是4,用1÷4,即可求出另一个内项。
【详解】1÷4=0.25
故答案为:D
【点睛】利用比例的基本性质、倒数的意义以及合数的认识进行解答。
2.D
【分析】由A÷2=B×5,可得A×=B×5,依据比例的基本性质,即两内项之积等于两外项之积,即可写出这个比例式,再化简即可。
【详解】由A÷2=B×5,可得A×=B×5
则:A∶B=5∶
5∶
=(5×2)∶(×2)
=10∶1
故答案为:D
【点睛】此题应根据比例的基本性质的逆运算进行解答。
3.C
【分析】根据比例尺=图上距离∶实际距离,代入数据,化简比即可;注意单位的换算:1m=100cm。
【详解】5cm∶10m
=5cm∶(10×100)cm
=5∶1000
=(5÷5)∶(1000÷5)
=1∶200
故答案为:C
【点睛】掌握图上距离、实际距离、比例尺三者之间的关系以及长度单位的换算是解题的关键。
4.D
【分析】设甲轮的半径为a,乙轮的半径为b;根据圆的周长公式:周长=π×半径×2;分别求出甲轮的周长是2πa和乙轮的周长2πb;又因为甲轮滚动2周的距离等于乙轮要滚动3周;列出等式,即2×2πa=3×2πb,再根据比例的基本性质:两个内项之积等于两个外项之积,求出两个滚轮的半径比,据此解答。
【详解】设甲滚轮的半径为a;乙滚轮的半径为b。
甲滚轮的周长:2πa
乙滚轮的周长:2πb
2×2πa=3×2πb
2πa=3πb
a∶b=3∶2
故答案为:D
【点睛】利用圆的周长公式和比例的基本性质进行解答。
5.C
【分析】圆柱、正方体、长方体的体积都等于底面积乘高,据此解答。
【详解】根据圆柱、正方体、长方体的体积公式,等底等高的圆柱、正方体、长方体的体积相比,它们的体积一样大。
故答案为:C
【点睛】牢固掌握圆柱、正方体和长方体的体积公式是解题的关键。
6.C
【分析】旋转是物体运动时,每一个点离同一个点(可以在物体外)的距离不变的运动,称为绕这个点的转动,这个点称为物体的转动中心,由此并结合实际可知:向左或向右转都是旋转了90°,向后转是旋转了180°;向左是逆时针,向右是顺时针,据此解答即可。
【详解】体育课上,老师喊的口令是“向后转”,你的身体应该顺时针旋转180°。
故答案为:C。
【点睛】解答此题的关键是明白:向左或向右转都是旋转了90°,向后转是旋转了180°。
7.正
【分析】判断两种相关联的量之间成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】在同一时间、同一地点,树的高和它的影长的比值是一定的,所以树的高和它的影长成正比例关系。
【点睛】此题属于辨识成正、反比例的量,就看这两种量是对应的比值一定,还是对应的乘积一定。
8.12
【分析】先判断哪两种相关联的量成何比例,即两个量的乘积一定则成反比例,两个量的比值一定则成正比例;根据题意,书的总量不变;每包的数量和包数成反比例;列出比例;解答即可。
【详解】解:设要捆x包。
30x=18×20
30x=360
x=360÷30
x=12
【点睛】根据正比例的应用和反比例的应用进行解答。
9.120
【分析】根据实际距离=图上距离÷比例尺,代入数据,即可解答。
【详解】3÷
=3×4000000
=12000000(厘米)
12000000厘米=120千米
【点睛】本题考查图上距离和实际距离的换算;注意单位名数的互换。
10. 785 1
【分析】根据圆柱体积公式的推导过程可知,把一个圆柱切拼成一个近似长方体体积不变,拼成的长方体的表面积比圆柱的表面积增加了两个切面(长方体的左右两个面)的面积,每个切面的长等于圆柱的高,宽等于圆柱的底面半径。根据圆柱的体积公式:V=πr2h,长方形的面积公式:S=ab,把数据代入公式解答。
【详解】3.14×52×10
=3.14×25×10
=785(立方厘米)
10×5×2=100(平方厘米)=1(平方分米)
【点睛】此题考查的目的是理解掌握圆柱体积公式的推导过程及应用,以及长方体的表面积、圆柱的体积公式及应用。
11. 60 20
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以等底等高的圆柱与圆锥的体积和相当于圆锥体积的(3+1)倍,根据已知一个数的几倍是多少,求这个数,用除法求出圆锥的体积,进而求出圆柱的体积。
【详解】圆锥的体积:80÷(3+1)
=80÷4
=20(cm3)
圆柱的体积:80-20=60(cm3)
【点睛】掌握等底等高的圆柱与圆锥体积的关系是解题的关键。
12. 169.56 113.04
【分析】根据题意,正方体削成一个最大的圆柱体,圆柱体的底面直径和高等于正方体的棱长;最大的圆锥体的底面直径等圆柱的底面直径;高等于圆柱的高;根据圆柱的体积公式:底面积×高;圆锥的体积公式:底面积×高×,代入数据,求出圆柱的体积和圆锥的体积,再用圆柱的体积减去圆锥的体积,即可解答。
【详解】圆柱的体积:3.14×(6÷2)2×6
=3.14×9×6
=28.26×6
=169.56(立方分米)
圆锥的体积:3.14×(6÷2)2×6×
=3.14×9×6×
=28.26×6×
=169.56×
=56.52(立方分米)
169.56-56.52=113.04(立方分米)
【点睛】利用圆柱的体积公式以及圆锥的体积公式进行解答,关键明确正方体内削最大的圆柱,圆柱的底面直径与高等于这个正方体的棱长。
13.√
【详解】略
14.×
【分析】等底等高的圆锥的体积是圆柱体积的,据此解答即可。
【详解】由分析可知:只有等底等高圆锥的体积是圆柱体积的,但题干中并没有强调圆柱和圆锥是等底等高的,所以原题干说法错误;
故答案为:×
【点睛】本题考查圆柱和圆锥的体积,明确圆柱和圆锥体积的关系是解题的关键。
15.错误
【详解】解:已完成的部分+未完成的部分=工作总量(一定),这两个相关联的量的和是定值,而它们没有乘除的关系,所以这两个相关联的量不成比例.原题说法错误.
故答案为错误
【分析】根据数量关系判断已完成的部分与未完成的部分的商一定还是积一定,如果商一定就成正比例,如果积一定就成反比例,否则不成比例.
16.×
【分析】圆柱的体积是由它的底面积和高两个条件决定的,而它的表面积=侧面积+底面积×2;除非它们的底面积和高分别相等,表面积才会相等,如果它们的底面积和高各不相等,表面积就不相等;可以举例来证明,由此解答即可。
【详解】比如,第一个圆柱体的底半径是r1=10,高是h1=1,
其体积为:V1=3.14×102×1
=3.14×100×1
=314
第二个圆柱的底半径是r2=5,高h2=4,
V2=3.14×52×4
=3.14×25×4
=78.5×4
=314
显然有V2=V1=314
但是S1=2×3.14×10×1+3.14×102×2
=6.28×10×1+314×2
=62.8+628
=690.8
S2=2×3.14×5×4+3.14×52×2
=6.28×5×4+78.5×2
=31.25×4+157
=125.6+157
=282.6
690.8≠282.6,表面积不相等;原题说法错误。
故答案为:×
【点睛】此题主要根据圆柱的体积和表面积的计算方法进行判断,可以通过举例来证明,更有说服力。
17.×
【详解】略
18.;2;;0.001;
;;;0;
【详解】略
19.300;12;7875;500
【详解】略
20.x=80;x=5;x=8
【分析】45%x=36,两边同时除以45%,方程得解;
13x-8x=25,合并成5x=25,两边同时除以5,即可求得方程的解;
6∶0.5=x∶利用比例的基本性质得:0.5x=6×,两边同时除以0.5,方程得解。
【详解】45%x=36
解:x=36÷45%
x=36÷0.45
x=80
13x-8x=25
解:5x=25
x=25÷5
x=5
6∶0.5=x∶
解:0.5x=6×
0.5x=4
x=4÷0.5
x=8
21.125.6立方厘米;3.14立方厘米
【分析】第一个是求圆柱的体积,已知底面半径和高,利用圆柱体积公式V=即可解答。
第二个是求圆锥的体积,也是已知底面半径和高,利用圆锥的体积公式V=,数值代入即可。
【详解】3.14××10
=3.14×4×10
=12.56×10
=125.6(立方厘米)
×3.14××3
=(×3)×3.14×1
=3.14(立方厘米)
22.10千克
【分析】根据题意可知,药粉∶水的质量比是1∶500;即药粉与水的比值一定,药粉与水的质量之间成正比例,等量关系:药粉∶水=1∶500,设配制这种农药需要药粉x千克,列比例:x∶5000=1∶500,解比例,即可解答。
【详解】解:设配制这种农药需要药粉x千克。
x∶5000=1∶500
500x=1×5000
500x=5000
x=5000÷500
x=10
答:配制这种农药需要药粉10千克。
【点睛】本题考查列方程解决问题和解比例,注意判断相关量的量是正比例还是反比例。
23.15小时
【分析】根据实际距离=图上距离÷比例尺,代入数据,求出甲、乙两地的实际距离,再根据时间=距离÷速度,代入数据,即可解答。
【详解】12÷
=12×7500000
=90000000(厘米)
90000000厘米=900千米
900÷60=15(小时)
答:需要15小时能走完全程。
【点睛】本题考查实际距离和图上距离的换算,以及利用速度、时间和距离三者关系进行解答,注意单位名数的换算。
24.0.25厘米
【分析】先根据圆锥的体积公式:V=,代入数据圆锥体铁块的体积,把铁块放入水中后,铁块的体积等于水面上升的体积,所以用铁块的体积除以圆柱的底面积,即可求出水面上升的高度。
【详解】
=
=
=(立方厘米)
=
=
=
=(厘米)
答:铁块放入后水面会上升0.25厘米。
【点睛】此题的解题关键是通过转化的数学思想,灵活运用圆柱和圆锥的体积公式求解。
25.(1)北;西;15
(2)见详解
【分析】(1)在地图上按照“上北下南,左西右东”确定方向,注意观测点是轮船A,测量出图上距离,然后根据图上距离和比例尺的关系确定实际距离。
(2)根据实际距离与比例尺的关系确定图上距离,再根据方位关系即可确定轮船C的位置。
【详解】(1)因为:经测量轮船B与轮船A之间的图上距离是3厘米,3×5=15(千米);
所以:轮船B在轮船A的北偏西50°方向15千米处。
(2)10÷5=2(厘米),画图如下:
【点睛】本题主要考查图上距离、实际距离与比例尺之间关系的灵活运用和根据方向、角度、距离确定物体位置的能力。
26.(1)成正比例,理由见解析。
(2)该工程队修路长度与相应时间关系的图像是一条直线,修路长度随着时间的增大而增大。
(3)900米。
【分析】(1)根据正比例的意义,求出修路长度与所用时间之间的关系,如果比值一定,就成正比例;据此解答。
(2)观察图像可知:正比例图像是一条直线,修路长度随着时间的增大而增大。
(3)根据“修路长度=每小时修路的长度×时间”,代入数据解答。
【详解】(1)该工程队修路长度与所用时间成正比例,
因为,是定值,所以该工程队修路长度与所用时间成正比例。
(2)由图可知:该工程队修路长度与相应时间关系的图像是一条直线,修路长度随着时间的增大而增大。
(3)9×100=900(米)
答:该工程队9小时修路900米。
【点睛】本题主要考查了正比例的判断、图像的认识、利用正比例关系解决实际问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
辽宁省沈阳市期末模拟测试卷(试题)2023-2024学年数学六年级下册北师大版
一、选择题
1.在一个比例中,已知两个外项互为倒数,其中一个内项是最小的合数,另一个内项是( )。
A.4 B.0.5 C.2 D.0.25
2.A÷2=B×5,A和B的最简整数比是( )。(A和B都不为0)
A.5∶1 B.2∶5 C.5∶2 D.10∶1
3.下图是六(1)班的教室平面图,亮亮在平面图上量得教室的长为5cm,这间教室的实际长是10m,这幅平面图的比例尺是( )。
A.1∶2 B.2∶1 C.1∶200 D.200∶1
4.甲乙两轮均为圆形,甲轮滚动2周的距离,乙轮要滚动3周,甲轮半径与乙轮半径的比是( )。
A.4∶9 B.9∶4 C.2∶3 D.3∶2
5.等底等高的圆柱、正方体、长方体的体积相比,( )。
A.长方体最大 B.正方体最大 C.一样大 D.圆柱最大
6.体育课上,老师喊的口令是“向后转”,你的身体应该( )。
A.顺时针旋转90° B.逆时针旋转90°
C.顺时针旋转180° D.逆时针旋转180°
二、填空题
7.同一时间、同一地点,树高和它的影子长成( )比例关系。
8.工人叔叔要包一批书,如果每包20本,要捆18包。如果每包30本,要捆( )包。
9.在比例尺为1∶4000000的地图上,量得A,B两地的距离是3厘米,A、B两地的实际距离是( )千米。
10.如图,将一个高10厘米、底面半径5厘米的圆柱平均分成32份,拼成一个近似的长方体,长方体的体积是( )立方厘米,表面积比原来增加了( )平方分米。
11.一个圆柱和圆锥等底等高,它们的体积和是80cm3,那么圆柱的体积是( )cm3,圆锥的体积是( )cm3。
12.如图,把一个棱长是6分米的正方体木料削成一个最大的圆柱,圆柱的体积是( )立方分米;再将圆柱削成一个最大的圆锥,还要再削去( )立方分米。
三、判断题
13.2018年第一季度有90天. ( )
14.一个圆锥的体积是6立方厘米,那么圆柱的体积是18立方厘米。( )
15.工作总量一定,已完成的部分与未完成的部分成反比例. ( )
16.体积相等的圆柱,它们的表面积也相等。( )
17.某校平面图的比例尺为米。 ( )
四、计算题
18.直接写得数.
×= ÷= 1-= 0.13= (+)×8=
-= += ×= 0÷= ÷3×÷3=
19.计算(能简算的要简算)
90÷÷50%
25×1.6×12.5
20.解方程。
45%x=36 13x-8x=25 6∶0.5=x∶
21.计算下面图形的体积。(单位:立方厘米)
五、解答题
22.配制一种农药,药粉和水的质量比是1∶500,现有水5000千克,配制这种农药需要药粉多少千克?(用比例解)
23.在比例尺是1∶7500000的地图上,量得甲、乙两地相距12厘米,一辆汽车以每小时60千米的速度从甲地开往乙地,需要多少小时能走完全程?
24.一个圆锥体铁块,底面半径是5厘米,高是3厘米,将这个圆锥体铁块放入到装有水的圆柱形容器中,完全浸没且没有水溢出,已知圆柱从里面量直径是20厘米,铁块放入后水面会上升多少厘米?
25.有三艘轮船在海面上航行。
(1)轮船在轮船的( )偏( )方向( )千米处。
(2)轮船在正东方向,距离轮船有10千米,请在图中标出轮船的位置。
26.下面是某工程队修路长度与所用时间的对应数值表。
修路长度/米 0 100 200 300 400 500
时间/小时 0 1 2 3 4 5
(1)该工程队修路长度与所用时间成正比例吗?为什么?
(2)下图是该工程队修路长度与相应时间关系的图像,说一说它有什么特点?
(3)照这样计算,该工程队9小时修路多少米?
参考答案:
1.D
【分析】根据比例的基本性质:两个外项之积等于两个内项之积;倒数的意义:乘积是1的两个数互为倒数;最小的合数是4;根据题意,两个外项互为倒数,即两个外项之积等于1,两个内项之积也等于1;其中一个内项是4,用1÷4,即可求出另一个内项。
【详解】1÷4=0.25
故答案为:D
【点睛】利用比例的基本性质、倒数的意义以及合数的认识进行解答。
2.D
【分析】由A÷2=B×5,可得A×=B×5,依据比例的基本性质,即两内项之积等于两外项之积,即可写出这个比例式,再化简即可。
【详解】由A÷2=B×5,可得A×=B×5
则:A∶B=5∶
5∶
=(5×2)∶(×2)
=10∶1
故答案为:D
【点睛】此题应根据比例的基本性质的逆运算进行解答。
3.C
【分析】根据比例尺=图上距离∶实际距离,代入数据,化简比即可;注意单位的换算:1m=100cm。
【详解】5cm∶10m
=5cm∶(10×100)cm
=5∶1000
=(5÷5)∶(1000÷5)
=1∶200
故答案为:C
【点睛】掌握图上距离、实际距离、比例尺三者之间的关系以及长度单位的换算是解题的关键。
4.D
【分析】设甲轮的半径为a,乙轮的半径为b;根据圆的周长公式:周长=π×半径×2;分别求出甲轮的周长是2πa和乙轮的周长2πb;又因为甲轮滚动2周的距离等于乙轮要滚动3周;列出等式,即2×2πa=3×2πb,再根据比例的基本性质:两个内项之积等于两个外项之积,求出两个滚轮的半径比,据此解答。
【详解】设甲滚轮的半径为a;乙滚轮的半径为b。
甲滚轮的周长:2πa
乙滚轮的周长:2πb
2×2πa=3×2πb
2πa=3πb
a∶b=3∶2
故答案为:D
【点睛】利用圆的周长公式和比例的基本性质进行解答。
5.C
【分析】圆柱、正方体、长方体的体积都等于底面积乘高,据此解答。
【详解】根据圆柱、正方体、长方体的体积公式,等底等高的圆柱、正方体、长方体的体积相比,它们的体积一样大。
故答案为:C
【点睛】牢固掌握圆柱、正方体和长方体的体积公式是解题的关键。
6.C
【分析】旋转是物体运动时,每一个点离同一个点(可以在物体外)的距离不变的运动,称为绕这个点的转动,这个点称为物体的转动中心,由此并结合实际可知:向左或向右转都是旋转了90°,向后转是旋转了180°;向左是逆时针,向右是顺时针,据此解答即可。
【详解】体育课上,老师喊的口令是“向后转”,你的身体应该顺时针旋转180°。
故答案为:C。
【点睛】解答此题的关键是明白:向左或向右转都是旋转了90°,向后转是旋转了180°。
7.正
【分析】判断两种相关联的量之间成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】在同一时间、同一地点,树的高和它的影长的比值是一定的,所以树的高和它的影长成正比例关系。
【点睛】此题属于辨识成正、反比例的量,就看这两种量是对应的比值一定,还是对应的乘积一定。
8.12
【分析】先判断哪两种相关联的量成何比例,即两个量的乘积一定则成反比例,两个量的比值一定则成正比例;根据题意,书的总量不变;每包的数量和包数成反比例;列出比例;解答即可。
【详解】解:设要捆x包。
30x=18×20
30x=360
x=360÷30
x=12
【点睛】根据正比例的应用和反比例的应用进行解答。
9.120
【分析】根据实际距离=图上距离÷比例尺,代入数据,即可解答。
【详解】3÷
=3×4000000
=12000000(厘米)
12000000厘米=120千米
【点睛】本题考查图上距离和实际距离的换算;注意单位名数的互换。
10. 785 1
【分析】根据圆柱体积公式的推导过程可知,把一个圆柱切拼成一个近似长方体体积不变,拼成的长方体的表面积比圆柱的表面积增加了两个切面(长方体的左右两个面)的面积,每个切面的长等于圆柱的高,宽等于圆柱的底面半径。根据圆柱的体积公式:V=πr2h,长方形的面积公式:S=ab,把数据代入公式解答。
【详解】3.14×52×10
=3.14×25×10
=785(立方厘米)
10×5×2=100(平方厘米)=1(平方分米)
【点睛】此题考查的目的是理解掌握圆柱体积公式的推导过程及应用,以及长方体的表面积、圆柱的体积公式及应用。
11. 60 20
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以等底等高的圆柱与圆锥的体积和相当于圆锥体积的(3+1)倍,根据已知一个数的几倍是多少,求这个数,用除法求出圆锥的体积,进而求出圆柱的体积。
【详解】圆锥的体积:80÷(3+1)
=80÷4
=20(cm3)
圆柱的体积:80-20=60(cm3)
【点睛】掌握等底等高的圆柱与圆锥体积的关系是解题的关键。
12. 169.56 113.04
【分析】根据题意,正方体削成一个最大的圆柱体,圆柱体的底面直径和高等于正方体的棱长;最大的圆锥体的底面直径等圆柱的底面直径;高等于圆柱的高;根据圆柱的体积公式:底面积×高;圆锥的体积公式:底面积×高×,代入数据,求出圆柱的体积和圆锥的体积,再用圆柱的体积减去圆锥的体积,即可解答。
【详解】圆柱的体积:3.14×(6÷2)2×6
=3.14×9×6
=28.26×6
=169.56(立方分米)
圆锥的体积:3.14×(6÷2)2×6×
=3.14×9×6×
=28.26×6×
=169.56×
=56.52(立方分米)
169.56-56.52=113.04(立方分米)
【点睛】利用圆柱的体积公式以及圆锥的体积公式进行解答,关键明确正方体内削最大的圆柱,圆柱的底面直径与高等于这个正方体的棱长。
13.√
【详解】略
14.×
【分析】等底等高的圆锥的体积是圆柱体积的,据此解答即可。
【详解】由分析可知:只有等底等高圆锥的体积是圆柱体积的,但题干中并没有强调圆柱和圆锥是等底等高的,所以原题干说法错误;
故答案为:×
【点睛】本题考查圆柱和圆锥的体积,明确圆柱和圆锥体积的关系是解题的关键。
15.错误
【详解】解:已完成的部分+未完成的部分=工作总量(一定),这两个相关联的量的和是定值,而它们没有乘除的关系,所以这两个相关联的量不成比例.原题说法错误.
故答案为错误
【分析】根据数量关系判断已完成的部分与未完成的部分的商一定还是积一定,如果商一定就成正比例,如果积一定就成反比例,否则不成比例.
16.×
【分析】圆柱的体积是由它的底面积和高两个条件决定的,而它的表面积=侧面积+底面积×2;除非它们的底面积和高分别相等,表面积才会相等,如果它们的底面积和高各不相等,表面积就不相等;可以举例来证明,由此解答即可。
【详解】比如,第一个圆柱体的底半径是r1=10,高是h1=1,
其体积为:V1=3.14×102×1
=3.14×100×1
=314
第二个圆柱的底半径是r2=5,高h2=4,
V2=3.14×52×4
=3.14×25×4
=78.5×4
=314
显然有V2=V1=314
但是S1=2×3.14×10×1+3.14×102×2
=6.28×10×1+314×2
=62.8+628
=690.8
S2=2×3.14×5×4+3.14×52×2
=6.28×5×4+78.5×2
=31.25×4+157
=125.6+157
=282.6
690.8≠282.6,表面积不相等;原题说法错误。
故答案为:×
【点睛】此题主要根据圆柱的体积和表面积的计算方法进行判断,可以通过举例来证明,更有说服力。
17.×
【详解】略
18.;2;;0.001;
;;;0;
【详解】略
19.300;12;7875;500
【详解】略
20.x=80;x=5;x=8
【分析】45%x=36,两边同时除以45%,方程得解;
13x-8x=25,合并成5x=25,两边同时除以5,即可求得方程的解;
6∶0.5=x∶利用比例的基本性质得:0.5x=6×,两边同时除以0.5,方程得解。
【详解】45%x=36
解:x=36÷45%
x=36÷0.45
x=80
13x-8x=25
解:5x=25
x=25÷5
x=5
6∶0.5=x∶
解:0.5x=6×
0.5x=4
x=4÷0.5
x=8
21.125.6立方厘米;3.14立方厘米
【分析】第一个是求圆柱的体积,已知底面半径和高,利用圆柱体积公式V=即可解答。
第二个是求圆锥的体积,也是已知底面半径和高,利用圆锥的体积公式V=,数值代入即可。
【详解】3.14××10
=3.14×4×10
=12.56×10
=125.6(立方厘米)
×3.14××3
=(×3)×3.14×1
=3.14(立方厘米)
22.10千克
【分析】根据题意可知,药粉∶水的质量比是1∶500;即药粉与水的比值一定,药粉与水的质量之间成正比例,等量关系:药粉∶水=1∶500,设配制这种农药需要药粉x千克,列比例:x∶5000=1∶500,解比例,即可解答。
【详解】解:设配制这种农药需要药粉x千克。
x∶5000=1∶500
500x=1×5000
500x=5000
x=5000÷500
x=10
答:配制这种农药需要药粉10千克。
【点睛】本题考查列方程解决问题和解比例,注意判断相关量的量是正比例还是反比例。
23.15小时
【分析】根据实际距离=图上距离÷比例尺,代入数据,求出甲、乙两地的实际距离,再根据时间=距离÷速度,代入数据,即可解答。
【详解】12÷
=12×7500000
=90000000(厘米)
90000000厘米=900千米
900÷60=15(小时)
答:需要15小时能走完全程。
【点睛】本题考查实际距离和图上距离的换算,以及利用速度、时间和距离三者关系进行解答,注意单位名数的换算。
24.0.25厘米
【分析】先根据圆锥的体积公式:V=,代入数据圆锥体铁块的体积,把铁块放入水中后,铁块的体积等于水面上升的体积,所以用铁块的体积除以圆柱的底面积,即可求出水面上升的高度。
【详解】
=
=
=(立方厘米)
=
=
=
=(厘米)
答:铁块放入后水面会上升0.25厘米。
【点睛】此题的解题关键是通过转化的数学思想,灵活运用圆柱和圆锥的体积公式求解。
25.(1)北;西;15
(2)见详解
【分析】(1)在地图上按照“上北下南,左西右东”确定方向,注意观测点是轮船A,测量出图上距离,然后根据图上距离和比例尺的关系确定实际距离。
(2)根据实际距离与比例尺的关系确定图上距离,再根据方位关系即可确定轮船C的位置。
【详解】(1)因为:经测量轮船B与轮船A之间的图上距离是3厘米,3×5=15(千米);
所以:轮船B在轮船A的北偏西50°方向15千米处。
(2)10÷5=2(厘米),画图如下:
【点睛】本题主要考查图上距离、实际距离与比例尺之间关系的灵活运用和根据方向、角度、距离确定物体位置的能力。
26.(1)成正比例,理由见解析。
(2)该工程队修路长度与相应时间关系的图像是一条直线,修路长度随着时间的增大而增大。
(3)900米。
【分析】(1)根据正比例的意义,求出修路长度与所用时间之间的关系,如果比值一定,就成正比例;据此解答。
(2)观察图像可知:正比例图像是一条直线,修路长度随着时间的增大而增大。
(3)根据“修路长度=每小时修路的长度×时间”,代入数据解答。
【详解】(1)该工程队修路长度与所用时间成正比例,
因为,是定值,所以该工程队修路长度与所用时间成正比例。
(2)由图可知:该工程队修路长度与相应时间关系的图像是一条直线,修路长度随着时间的增大而增大。
(3)9×100=900(米)
答:该工程队9小时修路900米。
【点睛】本题主要考查了正比例的判断、图像的认识、利用正比例关系解决实际问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
