第22章一元二次方程 章末复习 课件(共21张PPT)初中数学华师大版九年级上册
文档属性
| 名称 | 第22章一元二次方程 章末复习 课件(共21张PPT)初中数学华师大版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 110.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-10 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
章末复习
华东师大版九年级上册
复习目标:
掌握一元二次方程的基本概念及其解法;灵活运用一元二次方程知识解决一些实际问题.
复习重点:
一元二次方程的解法及应用.
复习难点:
一元二次方程的应用.
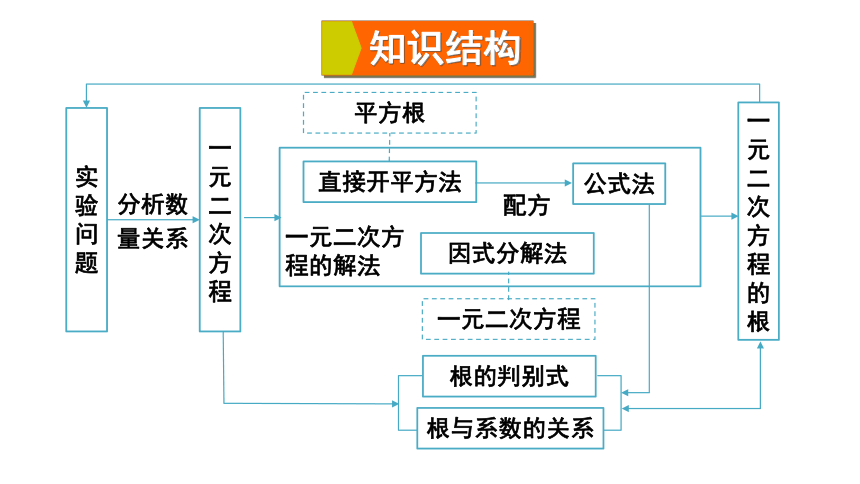
知识结构
实验问题
直接开平方法
公式法
因式分解法
一元二次方程
分析数量关系
配方
平方根
一元二次方程
一元二次方程的解法
一元二次方程的根
根的判别式
根与系数的关系
1.一元二次方程的解法
释疑解惑
方法名称 理论根据 使用方程的形式
直接开平方法
配方法
公式法
因式分解法
平方根的定义
完全平方公式
配方法
两个因式的积等于0,那么这两个因式至少有一个等于0
x2 = p 或 (mx + n)2 = p(p ≥ 0)
所有的一元二次方程
所有的一元二次方程
一边是0,另一边易于分解成两个一次因式的乘积的一元二次方程
①
②
③
优先选择
2. 一元二次方程根的判别式 Δ = b2 – 4ac
(1)当 Δ > 0 时,方程有两个不相等的实数根;
(2)当 Δ = 0 时,方程有两个相等的实数根;
(3)当 Δ < 0 时,方程无实数根.
在应用时,要根据根的情况限定 Δ 的取值,同时应注意二次项系数不为 0 这一条件.
3.一元二次方程 ax2 + bx + c = 0(a ≠ 0)的根与系数的关系,在应用时要注意变形. 同时要明确根与系数的关系成立的两个条件:
(1)a ≠ 0,(2)Δ ≥ 0
4. 应用一元二次方程解决实际问题,要注重分析实际问题中的等量关系,列出方程,求出方程的解,同时要注意检验其是否符合题意.
典例精析
用适当的方法解下列方程
(1)x2 + 12x + 27 = 0 (2)x(x – 2) + x – 2 = 0
(3)x2 + x – 2 = 4 (4)4(x + 2)2 = 9(2x – 1)2
例1
(1)(x + 3) (x + 9) = 0
x1 = – 3,x2 = – 9.
(2)(x + 1)(x – 2) = 0
x1 = – 1,x2 = 2.
解
(3)x2 + x – 6 = 0
(x – 2)(x + 3) = 0
解得 x1 = 2,x2 = – 3.
(4)32x2 – 52x – 7 = 0
(4x – 7)(8x + 1) = 0
关于 x 的方程 ax2 – (3a + 1)x + 2 (a + 1) = 0,有两个不相等的实数根 x1,x2,且有 x1 – x1x2 + x2 = 1 – a,则 a 的值是 ( ).
A.1 B. – 1 C.1或 – 1 D.2
例2
解得 a1 = 1,a2 = – 1.
a = 1 时 Δ = 0,方程有两个相等的实数根,与题意不符.
B
x1 – x1x2 + x2 = x1 + x2 – x1x2
为了倡导节能低碳生活,某公司对集体宿舍用电收费作如下规定:一间宿舍一个月用电量不超过 a 千瓦时,则一个月的电费为 20 元;若超过 a 千瓦时,则除交 20 元外,超过部分每千瓦
时要交 元,某宿舍 3 月份用电 80 千瓦时,交
电费 35 元;4 月份用电 45 千瓦时,交电费 20 元.
(1)求 a 的值;
(2)若该宿舍 5 月份交电费 45 元,那么 该宿舍当月用电量为多少千瓦时?
例3
a ≥ 45
解
(1)由题意得
20 + (80 – a)× = 35,
解得 a1 = 30,a2 = 50,
显然由题意可知 a ≥ 45,∴ a = 50.
(2)设 5 月份用电 x 千瓦时,依题意得
20 + (x – 50)× = 45,
解得 x = 100,
则该宿舍当月用电量为100千瓦时.
随堂演练
1.用配方法解方程 x2 + 4x + 1 = 0,配方后的方程是( )
A. (x + 2)2 = 3 B. (x – 2)2 = 3
C. (x – 2)2 = 5 D. (x + 2)2 = 5
A
2. 已知关于 x 的一元二次方程 (k – 2)2x2 + (2k + 1)x + 1 = 0 有两个不相等的实数根,则 k 的取值范围是( )
C
3.设 α,β 是一元二次方程 x2 + 3x – 7 = 0 的两个根,则 α2 + 4α + β = ____ .
α2 + 4α + β
= (α2 + 3α) + (α + β)
= 7 + (–3)
= 4
4
4.一学校为了绿化校园环境,向某园林公司购买了一批树苗,园林公司规定:如果购买树苗不超过 60 棵,每棵售价 120 元;如果购买树苗超过 60棵,每增加 1 棵,所出售的这批树苗每棵售价均降低 0.5 元,但每棵树苗最低售价不得少于 100 元.该校最终向园林公司支付树苗款 8800 元,请问该校共购买了多少棵树苗?
解:∵60 棵树苗的售价为 120×60 = 7200(元),而 7200 < 8800,
∴该校购买的树苗超过 60 棵.
设该校共购买了 x 棵树苗,由题意得
x[120 – 0.5(x – 60)] = 8800,
解得 x1 = 220,x2 = 80.
当 x1 = 220 时,120 – 0.5× ( 220 – 60 ) = 40 < 100,∴x = 220 不合题意,舍去;
当 x2 = 80 时,120 – 0.5× ( 80 – 60 ) = 110 > 100,∴ x = 80,即该校共购买了 80 棵树苗.
本堂课你能完整地回顾本章所学的有关一元二次方程的知识吗?你还有哪些困惑与疑问?
课堂小结
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
本课时通过学习归纳本章内容,让学生进一步系统掌握一元二次方程的解法及其应用,让学生懂得了如何应用一元二次方程的知识来解决生活中的实际问题,激发学生的学习兴趣.
章末复习
华东师大版九年级上册
复习目标:
掌握一元二次方程的基本概念及其解法;灵活运用一元二次方程知识解决一些实际问题.
复习重点:
一元二次方程的解法及应用.
复习难点:
一元二次方程的应用.
知识结构
实验问题
直接开平方法
公式法
因式分解法
一元二次方程
分析数量关系
配方
平方根
一元二次方程
一元二次方程的解法
一元二次方程的根
根的判别式
根与系数的关系
1.一元二次方程的解法
释疑解惑
方法名称 理论根据 使用方程的形式
直接开平方法
配方法
公式法
因式分解法
平方根的定义
完全平方公式
配方法
两个因式的积等于0,那么这两个因式至少有一个等于0
x2 = p 或 (mx + n)2 = p(p ≥ 0)
所有的一元二次方程
所有的一元二次方程
一边是0,另一边易于分解成两个一次因式的乘积的一元二次方程
①
②
③
优先选择
2. 一元二次方程根的判别式 Δ = b2 – 4ac
(1)当 Δ > 0 时,方程有两个不相等的实数根;
(2)当 Δ = 0 时,方程有两个相等的实数根;
(3)当 Δ < 0 时,方程无实数根.
在应用时,要根据根的情况限定 Δ 的取值,同时应注意二次项系数不为 0 这一条件.
3.一元二次方程 ax2 + bx + c = 0(a ≠ 0)的根与系数的关系,在应用时要注意变形. 同时要明确根与系数的关系成立的两个条件:
(1)a ≠ 0,(2)Δ ≥ 0
4. 应用一元二次方程解决实际问题,要注重分析实际问题中的等量关系,列出方程,求出方程的解,同时要注意检验其是否符合题意.
典例精析
用适当的方法解下列方程
(1)x2 + 12x + 27 = 0 (2)x(x – 2) + x – 2 = 0
(3)x2 + x – 2 = 4 (4)4(x + 2)2 = 9(2x – 1)2
例1
(1)(x + 3) (x + 9) = 0
x1 = – 3,x2 = – 9.
(2)(x + 1)(x – 2) = 0
x1 = – 1,x2 = 2.
解
(3)x2 + x – 6 = 0
(x – 2)(x + 3) = 0
解得 x1 = 2,x2 = – 3.
(4)32x2 – 52x – 7 = 0
(4x – 7)(8x + 1) = 0
关于 x 的方程 ax2 – (3a + 1)x + 2 (a + 1) = 0,有两个不相等的实数根 x1,x2,且有 x1 – x1x2 + x2 = 1 – a,则 a 的值是 ( ).
A.1 B. – 1 C.1或 – 1 D.2
例2
解得 a1 = 1,a2 = – 1.
a = 1 时 Δ = 0,方程有两个相等的实数根,与题意不符.
B
x1 – x1x2 + x2 = x1 + x2 – x1x2
为了倡导节能低碳生活,某公司对集体宿舍用电收费作如下规定:一间宿舍一个月用电量不超过 a 千瓦时,则一个月的电费为 20 元;若超过 a 千瓦时,则除交 20 元外,超过部分每千瓦
时要交 元,某宿舍 3 月份用电 80 千瓦时,交
电费 35 元;4 月份用电 45 千瓦时,交电费 20 元.
(1)求 a 的值;
(2)若该宿舍 5 月份交电费 45 元,那么 该宿舍当月用电量为多少千瓦时?
例3
a ≥ 45
解
(1)由题意得
20 + (80 – a)× = 35,
解得 a1 = 30,a2 = 50,
显然由题意可知 a ≥ 45,∴ a = 50.
(2)设 5 月份用电 x 千瓦时,依题意得
20 + (x – 50)× = 45,
解得 x = 100,
则该宿舍当月用电量为100千瓦时.
随堂演练
1.用配方法解方程 x2 + 4x + 1 = 0,配方后的方程是( )
A. (x + 2)2 = 3 B. (x – 2)2 = 3
C. (x – 2)2 = 5 D. (x + 2)2 = 5
A
2. 已知关于 x 的一元二次方程 (k – 2)2x2 + (2k + 1)x + 1 = 0 有两个不相等的实数根,则 k 的取值范围是( )
C
3.设 α,β 是一元二次方程 x2 + 3x – 7 = 0 的两个根,则 α2 + 4α + β = ____ .
α2 + 4α + β
= (α2 + 3α) + (α + β)
= 7 + (–3)
= 4
4
4.一学校为了绿化校园环境,向某园林公司购买了一批树苗,园林公司规定:如果购买树苗不超过 60 棵,每棵售价 120 元;如果购买树苗超过 60棵,每增加 1 棵,所出售的这批树苗每棵售价均降低 0.5 元,但每棵树苗最低售价不得少于 100 元.该校最终向园林公司支付树苗款 8800 元,请问该校共购买了多少棵树苗?
解:∵60 棵树苗的售价为 120×60 = 7200(元),而 7200 < 8800,
∴该校购买的树苗超过 60 棵.
设该校共购买了 x 棵树苗,由题意得
x[120 – 0.5(x – 60)] = 8800,
解得 x1 = 220,x2 = 80.
当 x1 = 220 时,120 – 0.5× ( 220 – 60 ) = 40 < 100,∴x = 220 不合题意,舍去;
当 x2 = 80 时,120 – 0.5× ( 80 – 60 ) = 110 > 100,∴ x = 80,即该校共购买了 80 棵树苗.
本堂课你能完整地回顾本章所学的有关一元二次方程的知识吗?你还有哪些困惑与疑问?
课堂小结
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
本课时通过学习归纳本章内容,让学生进一步系统掌握一元二次方程的解法及其应用,让学生懂得了如何应用一元二次方程的知识来解决生活中的实际问题,激发学生的学习兴趣.
