22.2.3. 公式法 课件(共22张PPT)初中数学华师大版九年级上册
文档属性
| 名称 | 22.2.3. 公式法 课件(共22张PPT)初中数学华师大版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 198.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-10 23:22:24 | ||
图片预览




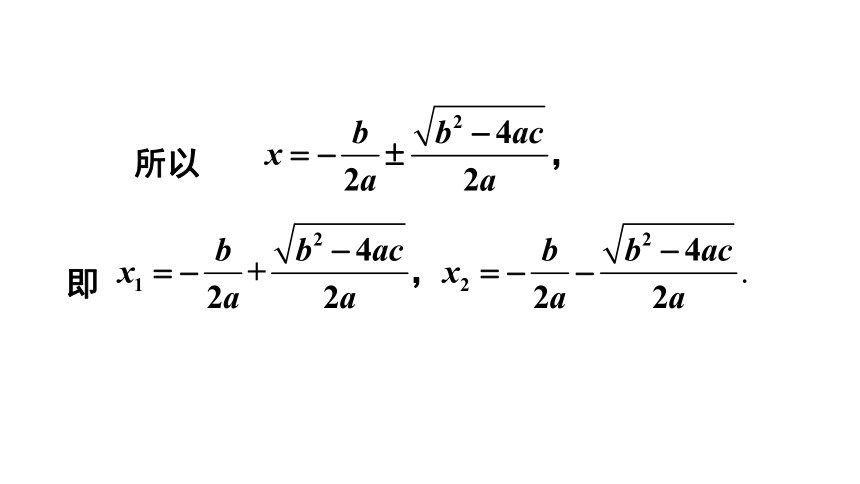




文档简介
(共22张PPT)
华东师大版九年级上册
22.2.3. 公式法
学习目标:
1. 理解一元二次方程求根公式的推导过程,了解公式法的概念.
2. 会熟练应用公式法解一元二次方程.
学习重点:
求根公式的推导和公式法的应用.
学习难点:
一元二次方程求根公式的推导.
探索
我们用配方法来解一般形式的一元二次方程
ax2 + bx + c = 0 (a ≠ 0).
因为 a ≠ 0,方程两边除以 a,得
移项,得
新课导入
配方,得
即
因为a ≠ 0,所以4a2 > 0.当 b2 – 4ac ≥ 0时,直接开平方,得
所以
即
由以上研究,得到了一元二次方程 ax2 + bx + c = 0 的求根公式.
将一元二次方程中系数 a、b、c 的值,直接代入这个公式,就可以求得方程的根.这种解一元二次方程的方法叫做公式法.
这里为什么要强调 b2 – 4ac ≥ 0 ?如果 b2 – 4ac < 0会怎样?
无解
推进新课
解下列方程:
(1)2x2 + x – 6 = 0; (2)x2 + 4x = 2;
(3)5x2 – 4x – 12 = 0;
(4)4x2 + 4x + 10 =1 – 8x.
例6
解
(1)a = 2,b = 1,c = – 6,
b2 – 4ac = 12 – 4×2×( – 6)
= 1 + 48 = 49 > 0,
所以
即
用公式法解一元二次方程的一般步骤:
1、把方程化成一般形式,并写出 a、b、c 的值.
2、求出 b2 – 4ac 的值.
3、代入求根公式 :
4、写出方程的解:x1、x2.
特别注意:当 b2 – 4ac < 0 时无解.
解
(2)将方程化为一般形式,得
x2 + 4x – 2 = 0.
因为 b2 – 4ac = 24,
所以
即
(3)因为 b2 – 4ac = 256,
所以
即
(4)整理,得
4x2 + 12x + 9 = 0.
因为 b2 – 4ac = 0,
所以
即
这里b2 – 4ac = 0 ,方程有两个相等 的实数根.
思考
根据你学习的体会小结一下:解一元二次方程有哪几种方法?通常你是如何选用的?和同学交流一下.
直接开平方法
因式分解法
配方法
公式法
应用
现在我们来解决 22.1 节中的问题 1:
x(x + 10) = 900,
x2 + 10x – 900 = 0,
它们都是所列方程的根,但负数根 x2 不符合题意,应舍去.
x + 10 ≈ 35.4,
符合题意,因此绿地的宽约为 25.4 米,长约为35.4 米.
随堂演练
用公式法解下列方程:
(1)x2 + x – 12=0
(3)x2 + 4x + 8 = 2x + 11
(4)x(x – 4) = 2 – 8x
(3)x2 + 4x + 8 = 2x + 11
解:移项化简,得
x2 + 2x – 3 = 0
(4)x(x – 4) = 2 – 8x
解:移项化简,得
x2 + 4x – 2 = 0
课堂小结
一元二次方程 ax2 + bx + c = 0 的求根公式.
将一元二次方程中系数 a、b、c 的值,直接代入这个公式,就可以求得方程的根.这种解一元二次方程的方法叫做公式法.
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
在学习活动中,要求学生主动参与,认真思考,比较观察,交流与表述,体验知识的获取的过程,激发学生的学习兴趣,利用师生的双边活动,适时调试,从而提高学习效率.
华东师大版九年级上册
22.2.3. 公式法
学习目标:
1. 理解一元二次方程求根公式的推导过程,了解公式法的概念.
2. 会熟练应用公式法解一元二次方程.
学习重点:
求根公式的推导和公式法的应用.
学习难点:
一元二次方程求根公式的推导.
探索
我们用配方法来解一般形式的一元二次方程
ax2 + bx + c = 0 (a ≠ 0).
因为 a ≠ 0,方程两边除以 a,得
移项,得
新课导入
配方,得
即
因为a ≠ 0,所以4a2 > 0.当 b2 – 4ac ≥ 0时,直接开平方,得
所以
即
由以上研究,得到了一元二次方程 ax2 + bx + c = 0 的求根公式.
将一元二次方程中系数 a、b、c 的值,直接代入这个公式,就可以求得方程的根.这种解一元二次方程的方法叫做公式法.
这里为什么要强调 b2 – 4ac ≥ 0 ?如果 b2 – 4ac < 0会怎样?
无解
推进新课
解下列方程:
(1)2x2 + x – 6 = 0; (2)x2 + 4x = 2;
(3)5x2 – 4x – 12 = 0;
(4)4x2 + 4x + 10 =1 – 8x.
例6
解
(1)a = 2,b = 1,c = – 6,
b2 – 4ac = 12 – 4×2×( – 6)
= 1 + 48 = 49 > 0,
所以
即
用公式法解一元二次方程的一般步骤:
1、把方程化成一般形式,并写出 a、b、c 的值.
2、求出 b2 – 4ac 的值.
3、代入求根公式 :
4、写出方程的解:x1、x2.
特别注意:当 b2 – 4ac < 0 时无解.
解
(2)将方程化为一般形式,得
x2 + 4x – 2 = 0.
因为 b2 – 4ac = 24,
所以
即
(3)因为 b2 – 4ac = 256,
所以
即
(4)整理,得
4x2 + 12x + 9 = 0.
因为 b2 – 4ac = 0,
所以
即
这里b2 – 4ac = 0 ,方程有两个相等 的实数根.
思考
根据你学习的体会小结一下:解一元二次方程有哪几种方法?通常你是如何选用的?和同学交流一下.
直接开平方法
因式分解法
配方法
公式法
应用
现在我们来解决 22.1 节中的问题 1:
x(x + 10) = 900,
x2 + 10x – 900 = 0,
它们都是所列方程的根,但负数根 x2 不符合题意,应舍去.
x + 10 ≈ 35.4,
符合题意,因此绿地的宽约为 25.4 米,长约为35.4 米.
随堂演练
用公式法解下列方程:
(1)x2 + x – 12=0
(3)x2 + 4x + 8 = 2x + 11
(4)x(x – 4) = 2 – 8x
(3)x2 + 4x + 8 = 2x + 11
解:移项化简,得
x2 + 2x – 3 = 0
(4)x(x – 4) = 2 – 8x
解:移项化简,得
x2 + 4x – 2 = 0
课堂小结
一元二次方程 ax2 + bx + c = 0 的求根公式.
将一元二次方程中系数 a、b、c 的值,直接代入这个公式,就可以求得方程的根.这种解一元二次方程的方法叫做公式法.
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
在学习活动中,要求学生主动参与,认真思考,比较观察,交流与表述,体验知识的获取的过程,激发学生的学习兴趣,利用师生的双边活动,适时调试,从而提高学习效率.
