22.2.5. 一元二次方程的根与系数的关系 课件(共17张PPT)初中数学华师大版九年级上册
文档属性
| 名称 | 22.2.5. 一元二次方程的根与系数的关系 课件(共17张PPT)初中数学华师大版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 117.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-10 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
华东师大版九年级上册
22.2.5. 一元二次方程的根与系数的关系
学习目标:
1. 能运用根的判别式,判断方程根的情况和进行有关的推理论证;
2. 会运用根的判别式求一元二次方程中字母系数的取值范围.
学习重点:
根的判别式的正确理解与运用.
学习难点:
含字母系数的一元二次方程根的判别式的应用.
求出一元二次方程 x2 + 3x – 4 = 0的两根 x1 和 x2,计算 x1 + x2 和 x1·x2 的值. 它们与方程的系数有什么关系?
新课导入
试 一 试
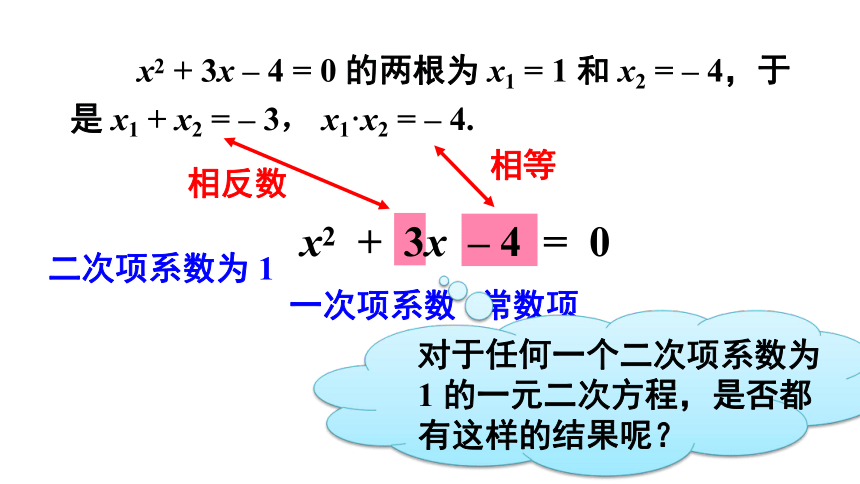
x2 + 3x – 4 = 0 的两根为 x1 = 1 和 x2 = – 4,于是 x1 + x2 = – 3, x1·x2 = – 4.
x2 + 3x – 4 = 0
二次项系数为 1
一次项系数
常数项
相反数
相等
对于任何一个二次项系数为 1 的一元二次方程,是否都有这样的结果呢?
探索
我们来考察方程 x2 + px + q = 0(p2 – 4q ≥ 0).
由一元二次方程的求根公式,得到方程的两根分别为
推进新课
所以
概括
二次项系数为 1 的一元二次方程根与系数的关系:
设一元二次方程 x2 + px + q = 0 的两根为x1、x2,那么
x1 + x2 = – p ,x1·x2 = q.
不解方程,求出方程的两根之和和两根之积:
(1)x2 + 3x – 5 = 0;
(2)2x2 – 3x – 5 = 0;
例8
解
(1)设两根为 x1、x2,由上述二次项系数为 1 的一元二次方程根与系数的关系,可得
x1 + x2 = – 3 ,x1·x2 = – 5 .
(2)方程两边同除以 2 ,得
设两根为 x1、x2 ,可得
试探索一元二次方程 ax2 + bx + c = 0 (a ≠ 0,b2 – 4ac ≥ 0)的根与系数的关系.
例9
解
方程两边同除以 a ,得
由二次项系数为 1 的一元二次方程根与系数的关系,可得
这就是一般情形下一元二次方程的根与系数的关系.
前面概括的结论是它的特例(二次项系数为1).
随堂演练
1. 不解方程,求下列方程的两根之和与两根之积:
(1)(x + 1)(x – 2) = 0;
(2)3x2 + 7x = 6.
(1)x1 + x2 = 1,x1·x2 = – 2 .
x2 – x – 2 = 0
3x2 + 7x – 6 = 0
2. 两根均为负数的一元二次方程是( )
A. 7x2 – 12x + 5 = 0
B. 6x2 – 13x – 5 = 0
C. 4x2 + 21x + 5 = 0
D. x2 + 15x – 8 = 0
C
x1 + x2 < 0,x1·x2 > 0.
3.已知 α,β 是方程 x2 – 3x – 5 = 0的两根,不解方程,求下列代数式的值.
(2) α2 + β2 (3) α – β
(2)α2 + β2 = (α + β)2 – 2αβ = 32 – 2× (–5) = 19;
(3)(α – β)2 = (α + β)2 – 4αβ = 29,
课堂小结
一元二次方程 ax2 + bx + c = 0 (a ≠ 0,b2 – 4ac ≥ 0)的根与系数的关系:
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
本节课先由学生探究特殊一元二次方程的根与系数的关系,再猜想一般一元二次方程的根与系数的关系,并从理论上加以推导证明,加深学生对知识的理解,培养学生严密的逻辑思维能力.
华东师大版九年级上册
22.2.5. 一元二次方程的根与系数的关系
学习目标:
1. 能运用根的判别式,判断方程根的情况和进行有关的推理论证;
2. 会运用根的判别式求一元二次方程中字母系数的取值范围.
学习重点:
根的判别式的正确理解与运用.
学习难点:
含字母系数的一元二次方程根的判别式的应用.
求出一元二次方程 x2 + 3x – 4 = 0的两根 x1 和 x2,计算 x1 + x2 和 x1·x2 的值. 它们与方程的系数有什么关系?
新课导入
试 一 试
x2 + 3x – 4 = 0 的两根为 x1 = 1 和 x2 = – 4,于是 x1 + x2 = – 3, x1·x2 = – 4.
x2 + 3x – 4 = 0
二次项系数为 1
一次项系数
常数项
相反数
相等
对于任何一个二次项系数为 1 的一元二次方程,是否都有这样的结果呢?
探索
我们来考察方程 x2 + px + q = 0(p2 – 4q ≥ 0).
由一元二次方程的求根公式,得到方程的两根分别为
推进新课
所以
概括
二次项系数为 1 的一元二次方程根与系数的关系:
设一元二次方程 x2 + px + q = 0 的两根为x1、x2,那么
x1 + x2 = – p ,x1·x2 = q.
不解方程,求出方程的两根之和和两根之积:
(1)x2 + 3x – 5 = 0;
(2)2x2 – 3x – 5 = 0;
例8
解
(1)设两根为 x1、x2,由上述二次项系数为 1 的一元二次方程根与系数的关系,可得
x1 + x2 = – 3 ,x1·x2 = – 5 .
(2)方程两边同除以 2 ,得
设两根为 x1、x2 ,可得
试探索一元二次方程 ax2 + bx + c = 0 (a ≠ 0,b2 – 4ac ≥ 0)的根与系数的关系.
例9
解
方程两边同除以 a ,得
由二次项系数为 1 的一元二次方程根与系数的关系,可得
这就是一般情形下一元二次方程的根与系数的关系.
前面概括的结论是它的特例(二次项系数为1).
随堂演练
1. 不解方程,求下列方程的两根之和与两根之积:
(1)(x + 1)(x – 2) = 0;
(2)3x2 + 7x = 6.
(1)x1 + x2 = 1,x1·x2 = – 2 .
x2 – x – 2 = 0
3x2 + 7x – 6 = 0
2. 两根均为负数的一元二次方程是( )
A. 7x2 – 12x + 5 = 0
B. 6x2 – 13x – 5 = 0
C. 4x2 + 21x + 5 = 0
D. x2 + 15x – 8 = 0
C
x1 + x2 < 0,x1·x2 > 0.
3.已知 α,β 是方程 x2 – 3x – 5 = 0的两根,不解方程,求下列代数式的值.
(2) α2 + β2 (3) α – β
(2)α2 + β2 = (α + β)2 – 2αβ = 32 – 2× (–5) = 19;
(3)(α – β)2 = (α + β)2 – 4αβ = 29,
课堂小结
一元二次方程 ax2 + bx + c = 0 (a ≠ 0,b2 – 4ac ≥ 0)的根与系数的关系:
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
本节课先由学生探究特殊一元二次方程的根与系数的关系,再猜想一般一元二次方程的根与系数的关系,并从理论上加以推导证明,加深学生对知识的理解,培养学生严密的逻辑思维能力.
