23.3.2 第1课时 相似三角形的判定(1) 课件(共21张PPT)初中数学华师大版九年级上册
文档属性
| 名称 | 23.3.2 第1课时 相似三角形的判定(1) 课件(共21张PPT)初中数学华师大版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 227.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-10 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
2.相似三角形的判定
华东师大版九年级上册
第1课时 相似三角形的判定(1)
学习目标:
会说判定两个三角形相似的方法:两角分别相等的两个三角形相似.会用这种方法判断两个三角形是否相似.
学习重点:
相似三角形的判定定理 1 以及推导过程,并会用判定定理 1 来证明和计算.
学习难点:
相似三角形的判定定理 1 的运用.
如何判断两个三角形是否相似?
复习导入
根据定义:对应角相等,对应边成比例.
是否存在判定两个三角形相似的简便方法?
推进新课
在判定两个三角形全等时,我们得到了SSS,SAS,ASA,AAS的简便方法.
那么,对于相似三角形的判定,是否也存在类似的分类与判定方法呢?
回顾
从直观来看,一个三角形的三个角分别与另一个三角形的三个角对应相等时,它们就“应该”相似了.确实是这样吗?
直角三角尺
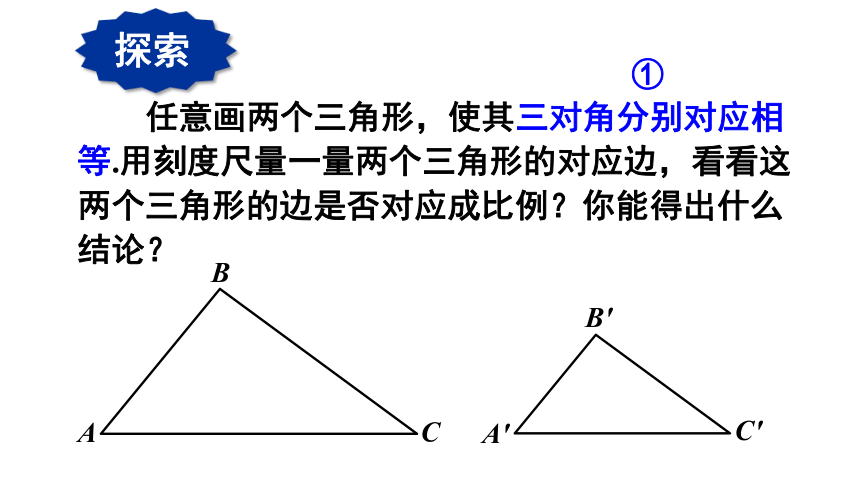
任意画两个三角形,使其三对角分别对应相等.用刻度尺量一量两个三角形的对应边,看看这两个三角形的边是否对应成比例?你能得出什么结论?
探索
B
A
C
B'
A'
C'
①
于是这两个三角形相似.
B
A
C
B'
A'
C'
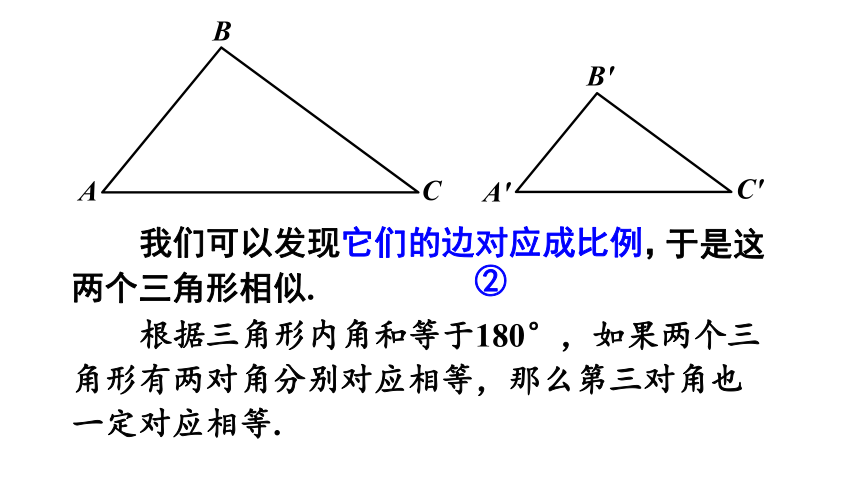
我们可以发现它们的边对应成比例,
根据三角形内角和等于180°,如果两个三角形有两对角分别对应相等,那么第三对角也 一定对应相等.
②
相似三角形的判定定理1 两角分别相等的两个三角形相似.
判定两个三角形相似的一个较简便的方法:
A
B
C
已知:如图,在△ABC 和△A1B1C1中,∠A = ∠A1,∠B =∠B1 .
求证:△ABC ∽ △A1B1C1.
A1
B1
C1
在边 AB 或它的延长线上截取 AD = A1B1,过点 D 作 BC 的平行线交 AC 于点 E,得
△ADE ∽ △ABC .
证明
A
B
C
D
E
A1
B1
C1
∵ DE∥BC ,
∴ ∠ADE = ∠B .
在△ADE 与△A1B1C1 中,
∵ ∠A =∠A1,∠ADE =∠B =∠B1 ,AD = A1B1 ,
∴ △ADE ≌△A1B1C1.
∴ △ABC ∽ △A1B1C1.
全等变换
如果两个三角形仅有一对角是对应相等的,那么它们是否一定相似?
思考
如图,在Rt△ABC 和Rt△A′B′C′ 中,∠C 与∠C′ 都是直角,∠A =∠A′.求证:△ABC ∽△A′B′C′ .
例2
解
∵ ∠C =∠C′ = 90°,
∠A =∠A′ ,
∴ △ABC ∽△A′B′C′ (两角分别相等的两个三角形相似).
两个直角三角形,若有一对锐角对应相等,则它们一定相似.
A
B
C
D
E
F
如图,在△ABC 中,DE∥BC,EF∥AB,求证:△ADE ∽ △EFC.
例3
∵ DE∥BC ,
∴ ∠ADE = ∠B,∠AED = ∠C,
又∵ EF∥AB,
∴∠EFC =∠B ,
∴∠ADE =∠EFC,
∴△ADE∽△EFC (两角分别相等的两个三角形相似).
证明
想 一 想
在例3 中,如果点 D 恰好在边AB 的中点,那么点 E 是边 AC 的中点吗?此时,DE 和 BC 有什么关系?△ADE 与 △EFC 又有什么特殊关系呢?
A
B
C
E 是边 AC 的中点,
△ADE ≌ △EFC .
D
E
F
D
E
F
随堂演练
1. △ABC 中,∠ACB = 90°,CD⊥AB 于 D,找出图中所有的相似三角形.
A
B
C
D
△ABC ∽△ACD∽△CBD
2.△ABC中,D 是 AB 的边上一点,过点 D 作一直线与 AC 相交于 E,要使 △ADE 与 △ABC 相似,你怎样画这条直线?说明理由. 和你的同伴交流作法是否一样.
A
C
B
D
A
C
B
D
有两种不同的画法:
①过 D 点作 DE∥BC,DE 交 AC 于点 E;
②以 AD 为一边在△ABC 内部作∠ADE =∠C,另一边 DE 交 AC 于点 E.
E
E
课堂小结
判定两个三角形相似的一个较简便的方法:
相似三角形的判定定理1 两角分别相等的两个三角形相似.
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
本课时从学生所熟悉的特殊三角板入手,通过学生动手操作探究相似三角形的判定定理 1,从中感受学习几何的乐趣,从而激发学生学习兴趣,培养学生的几何推理能力.
2.相似三角形的判定
华东师大版九年级上册
第1课时 相似三角形的判定(1)
学习目标:
会说判定两个三角形相似的方法:两角分别相等的两个三角形相似.会用这种方法判断两个三角形是否相似.
学习重点:
相似三角形的判定定理 1 以及推导过程,并会用判定定理 1 来证明和计算.
学习难点:
相似三角形的判定定理 1 的运用.
如何判断两个三角形是否相似?
复习导入
根据定义:对应角相等,对应边成比例.
是否存在判定两个三角形相似的简便方法?
推进新课
在判定两个三角形全等时,我们得到了SSS,SAS,ASA,AAS的简便方法.
那么,对于相似三角形的判定,是否也存在类似的分类与判定方法呢?
回顾
从直观来看,一个三角形的三个角分别与另一个三角形的三个角对应相等时,它们就“应该”相似了.确实是这样吗?
直角三角尺
任意画两个三角形,使其三对角分别对应相等.用刻度尺量一量两个三角形的对应边,看看这两个三角形的边是否对应成比例?你能得出什么结论?
探索
B
A
C
B'
A'
C'
①
于是这两个三角形相似.
B
A
C
B'
A'
C'
我们可以发现它们的边对应成比例,
根据三角形内角和等于180°,如果两个三角形有两对角分别对应相等,那么第三对角也 一定对应相等.
②
相似三角形的判定定理1 两角分别相等的两个三角形相似.
判定两个三角形相似的一个较简便的方法:
A
B
C
已知:如图,在△ABC 和△A1B1C1中,∠A = ∠A1,∠B =∠B1 .
求证:△ABC ∽ △A1B1C1.
A1
B1
C1
在边 AB 或它的延长线上截取 AD = A1B1,过点 D 作 BC 的平行线交 AC 于点 E,得
△ADE ∽ △ABC .
证明
A
B
C
D
E
A1
B1
C1
∵ DE∥BC ,
∴ ∠ADE = ∠B .
在△ADE 与△A1B1C1 中,
∵ ∠A =∠A1,∠ADE =∠B =∠B1 ,AD = A1B1 ,
∴ △ADE ≌△A1B1C1.
∴ △ABC ∽ △A1B1C1.
全等变换
如果两个三角形仅有一对角是对应相等的,那么它们是否一定相似?
思考
如图,在Rt△ABC 和Rt△A′B′C′ 中,∠C 与∠C′ 都是直角,∠A =∠A′.求证:△ABC ∽△A′B′C′ .
例2
解
∵ ∠C =∠C′ = 90°,
∠A =∠A′ ,
∴ △ABC ∽△A′B′C′ (两角分别相等的两个三角形相似).
两个直角三角形,若有一对锐角对应相等,则它们一定相似.
A
B
C
D
E
F
如图,在△ABC 中,DE∥BC,EF∥AB,求证:△ADE ∽ △EFC.
例3
∵ DE∥BC ,
∴ ∠ADE = ∠B,∠AED = ∠C,
又∵ EF∥AB,
∴∠EFC =∠B ,
∴∠ADE =∠EFC,
∴△ADE∽△EFC (两角分别相等的两个三角形相似).
证明
想 一 想
在例3 中,如果点 D 恰好在边AB 的中点,那么点 E 是边 AC 的中点吗?此时,DE 和 BC 有什么关系?△ADE 与 △EFC 又有什么特殊关系呢?
A
B
C
E 是边 AC 的中点,
△ADE ≌ △EFC .
D
E
F
D
E
F
随堂演练
1. △ABC 中,∠ACB = 90°,CD⊥AB 于 D,找出图中所有的相似三角形.
A
B
C
D
△ABC ∽△ACD∽△CBD
2.△ABC中,D 是 AB 的边上一点,过点 D 作一直线与 AC 相交于 E,要使 △ADE 与 △ABC 相似,你怎样画这条直线?说明理由. 和你的同伴交流作法是否一样.
A
C
B
D
A
C
B
D
有两种不同的画法:
①过 D 点作 DE∥BC,DE 交 AC 于点 E;
②以 AD 为一边在△ABC 内部作∠ADE =∠C,另一边 DE 交 AC 于点 E.
E
E
课堂小结
判定两个三角形相似的一个较简便的方法:
相似三角形的判定定理1 两角分别相等的两个三角形相似.
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
本课时从学生所熟悉的特殊三角板入手,通过学生动手操作探究相似三角形的判定定理 1,从中感受学习几何的乐趣,从而激发学生学习兴趣,培养学生的几何推理能力.
