2023-2024学年青岛版小学数学六年级下册《期末常考易错检测卷》试题(含答案解析)
文档属性
| 名称 | 2023-2024学年青岛版小学数学六年级下册《期末常考易错检测卷》试题(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 241.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-10 21:39:26 | ||
图片预览




文档简介
期末常考易错检测卷(试题)2023-2024学年数学六年级下册青岛版
一、选择题
1.在下面各比中,能组成比例的是( )。
A.4∶3和∶3 B.3∶4和∶ C.3∶4和∶3 D.4∶3和∶
2.下面两种相关联的量成反比例的是( )。
A.互为倒数关系的A和B B.圆柱的高一定,它的体积和底面积
C.被减数一定,减数与差 D.长方形的宽一定,它的长和面积
3.“争创文明城,共建新枣庄”,六、2班有15人参加创城志愿者服务,比六、1班志愿者人数少4人,以下问题能用算式(15+4)÷15解决的是( )。
A.六、1班志愿者人数是六、2班志愿者人数的百分之几?
B.六、2班志愿者人数是六、1班志愿者人数的百分之几?
C.六、1班志愿者人数比六、2班志愿者人数多百分之几?
D.六、2班志愿者人数比六、1班志愿者人数少百分之几?
4.把一个棱长4分米的正方体木块削成一个最大的圆柱体,体积是( )立方分米。
A.200.96 B.100.48 C.64 D.50.24
5.一种商品先提价20%,再打八折,现价与原价相比,( )。
A.比原价高 B.比原价低 C.与原价相等 D.无法比较
6.我国逐渐完善养老金制度,居民可自行缴纳养老金。甲、乙两人计划用相同的年数分别缴纳养老金18万元和12万元。甲计划每年比乙多缴纳保险金0.2万元。若乙每年缴纳保险金x万元,则根据题意可列出比例为( )。
A. B.
C. D.
二、填空题
7.0.6=( )%=( )成=( )÷( )。
8.一支钢笔,打八折卖出亏10元,打九折卖出赚15元,则这件商品的标价是( )元,若卖218元,可赚( )元。
9.明明把2000元钱存入银行,定期两年,年利率是2.25%,到期后一共可以取回( )元。
10.如表中,如果x和y成正比例,空格里的数是( );如果x和y成反比例,空格里的数是( )。
y 2.4 6
x 10
11.把一段圆柱体木材料削成一个最大的圆锥,削去部分的体积是16立方厘米,这个圆锥的体积是( )立方厘米。
12.一个圆柱和圆锥的底面半径和高分别相等,已知圆锥体积比圆柱的体积少16立方米,圆柱的体积( )立方米,圆柱的体积比圆锥的体积多( )%。
三、判断题
13.如果a∶b=,那么4a=3b。( )
14.一件商品,降价20元后卖180元,这件商品折扣是八折。( )
15.在一个比例中,两个外项的积减去两个内项的积,差为0。( )
16.有一个圆柱的底面直径和高相等,它的侧面可以展开成一个正方形。( )
17.从圆锥的顶点沿高切成两部分,得到的截面一定是等腰三角形。( )
四、计算题
18.直接写得数。
19.计算下面各题。
20.解比例。
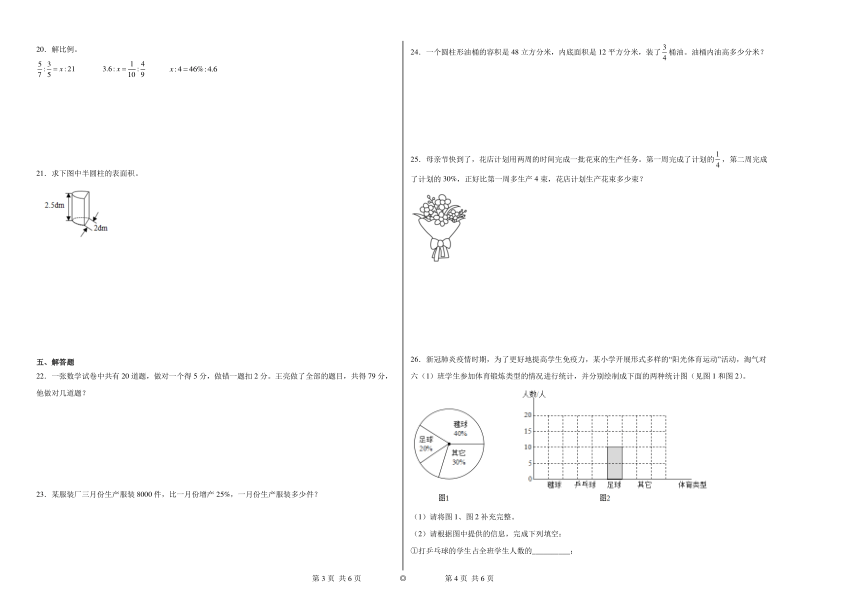
21.求下图中半圆柱的表面积。
五、解答题
22.一张数学试卷中共有20道题,做对一个得5分,做错一题扣2分。王亮做了全部的题目,共得79分,他做对几道题?
23.某服装厂三月份生产服装8000件,比一月份增产25%,一月份生产服装多少件?
24.一个圆柱形油桶的容积是48立方分米,内底面积是12平方分米,装了桶油。油桶内油高多少分米?
25.母亲节快到了,花店计划用两周的时间完成一批花束的生产任务。第一周完成了计划的,第二周完成了计划的30%,正好比第一周多生产4束,花店计划生产花束多少束?
26.新冠肺炎疫情时期,为了更好地提高学生免疫力,某小学开展形式多样的“阳光体育运动”活动,淘气对六(1)班学生参加体育锻炼类型的情况进行统计,并分别绘制成下面的两种统计图(见图1和图2)。
(1)请将图1、图2补充完整。
(2)请根据图中提供的信息,完成下列填空:
①打乒乓球的学生占全班学生人数的__________;
②六(1)班学生共有__________人;
③踢毽球的学生人数比打乒乓球的人数多__________人。
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】判断两个比能不能组成比例,可以分别求出比值,比值相等,能组成比例,否则,不能组成比例,据此解答。
【详解】A.4∶3
=4÷3
=
∶3
=÷3
=×
=
≠,所以4∶3和∶3不能组成比例;
B.3∶4
=3÷4
=
∶
=÷
=×3
=
=,所以3∶4=∶,能组成比例;
C.3∶4
=3÷4
=
∶3
=÷3
=×
=
≠,所以3∶4和∶3不能组成比例;
D.4∶3
=4÷3
=
∶
=÷
=×3
=
≠,所以4∶3和∶不能组成比例;
故答案为:B
2.A
【分析】两种相关联的量,若两种量的比值一定,两种量成正比例;若两种量的乘积一定,两种量成反比例;若两种量既不存在比值一定,又不存在乘积一定,两种量不成比例。据此解答。
【详解】A.A和B互为倒数,则AB=1,A和B的乘积一定,A和B成反比例;
B.圆柱的高=体积÷底面积,圆柱的高一定时,它的体积和底面积成正比例;
C.被减数=减数+差,被减数一定时,减数与差不成比例;
D.长方形的宽=面积÷长,长方形的宽一定时,它的长和面积成正比例。
故答案为:A
【点睛】辨识两种相关联的量成正比例还是成反比例,就看这两种量是比值一定,还是乘积一定。
3.A
【分析】根据题意可知,(15+4)求的是六、1班志愿者的人数,是被除数;除数15是六、2班的人数,把15看作单位“1”,所以此算式求的是六、1班志愿者人数是六、2班志愿者人数的百分之几据此即可解答。
【详解】能用算式(15+4)÷15解决的是六、1班志愿者人数是六、2班志愿者人数的百分之几?
故答案为:A
【点睛】本题是求一个数是另一个数的百分之几,关键是看把谁当成了单位“1”,单位“1”的量为除数。
4.D
【分析】正方体内削出的最大圆柱的底面直径和高都等于这个正方体的棱长,由此利用圆柱的体积公式:,即可解答。
【详解】3.14×(4÷2)2×4
=3.14×4×4
=50.24(立方分米)
故答案为:D
5.B
【分析】假设这种商品的价格1,并把它看成单位“1”,提高后的价格是原价的(1+20%),由此用乘法求出提高后的价格;
再把提高后的价格看成单位“1”,再打八折出售即现价是提高后价格的80%,由此用乘法求出现价,再比较原价和现价即可。
【详解】假设原价是1;
1×(1+20%)×80%
=1×120%×80%
=0.96
1>0.96
现价比原价低。
故答案为:B
6.B
【分析】设乙每年缴纳养老保险为x万元,则甲每年缴纳养老保险金为(x+0.2)万元,根据甲、乙两人计划用相同的年数分别缴纳养老保险金18万元和12万元可知,18比上(x+0.2)万元等于12比上x万元。
【详解】根据题意可列出比例为。
故答案为:B
7.21;60;六;3;5
【分析】分数的分子相当于被除数,分母相当于除数,分数的分子和分母,同时乘或除以相同的数(0除外),分数的大小不变。据此先将小数化成分数,根据分数与除法的关系,以及它们通用的基本性质进行填空,小数化百分数,小数点向右移动两位,添上百分号即可,根据几成就是百分之几十,确定成数。
【详解】0.6==3÷5,35÷5×3=21;0.6=60%=六成
0.6=60%=六成=3÷5
8. 250 8
【分析】由题意可知,标价的80%加上10,与标价的90%减去15都表示钢笔的进价。根据这一数量关系求商品的标价,可以列方程解答。然后用标价乘80%再加10求出进价,最后用218减去进价,可算出赚了多少钱。据此解答。
【详解】解:设钢笔的标价为x元。
90%x-15=80%x+10
0.9x-0.8x=15+10
0.1x=25
x=250
218-(250×80%+10)
=218-(200+10)
=218-210
=8(元)
所以,这件商品的标价是250元,若卖218元,可赚8元。
9.2090
【分析】取回的钱包括本金和利息,利息=本金×利率×存期,本金+利息=可以取回的钱,据此列式计算。
【详解】2000+2000×2.25%×2
=2000+2000×0.0225×2
=2000+90
=2090(元)
到期后一共可以取回2090元。
10. 4 25
【分析】因为x和y成正比例,所以y∶x是定值,而y∶x=6∶10=0.6,由此求出x的值;因为x和y成反比例,所以x与y的乘积是定值,而xy=6×10=60,由此求出x的值。
【详解】y∶x
=6∶10
=0.6
所以x=2.4÷0.6=4;
因为xy=6×10=60,所以x=60÷2.4=25。
11.8
【分析】圆柱内最大的圆锥与原来圆柱是等底等高的,所以圆锥的体积是圆柱的体积是的,则圆锥的体积就是削去部分的体积的,由此即可解答。
【详解】16×=8(立方厘米)
这个圆锥的体积是8立方厘米。
12. 24 200
【分析】等底等高的圆锥的体积是圆柱的,所以这里的体积之差就是圆柱的,由此可得圆柱的体积就是16÷=24(立方厘米),再用圆柱体积与圆锥体积的差除以圆锥的体积,计算圆柱比圆锥体积多百分之几即可。
【详解】16÷(1-)
=16÷
=24(立方厘米)
24×=8(立方米)
(24-8)÷8
=16÷8
=200%
圆柱的体积是(24)立方厘米,圆柱的体积比圆锥的体积多(200)%。
13.√
【分析】将分数写成比的形式,根据比例的基本性质,比例的两内项积=两外项积,进行分析。
【详解】=3∶4,a∶b=3∶4,根据比例的基本性质,可得4a=3b,原题说法正确。
故答案为:√
14.×
【分析】先求出原价,降价后价格÷原价=现价是原价的百分之几,根据几折就是百分之几十,确定折数。
【详解】180÷(180+20)
=180÷200
=0.9
=90%
一件商品,降价20元后卖180元,这件商品折扣是九折,原题说法错误。
故答案为:×
15.√
【分析】比例的基本性质:在比例里,两个外项的积等于两个内项的积。
【详解】在一个比例中,两个外项的积等于两个内项的积,所以两个外项的积减去两个内项的积,差为0。
原题说法正确。
故答案为:√
16.×
【分析】圆柱侧面展开图是个正方形,说明圆柱底面周长=圆柱的高,据此分析。
【详解】有一个圆柱的底面直径和高相等,沿着直径切开的剖面是个正方形,侧面展开是个长方形,原题说法错误。
故答案为:×
【点睛】关键是熟悉圆柱特征,理解圆柱侧面展开图和圆柱之间的关系。
17.√
【分析】根据圆锥的特征,圆锥沿高切成两部分,切面是以底面直径为底、以圆锥的高为高的等腰三角形。
【详解】
如图所示:从圆锥的顶点沿高切成两部分,得到的截面是等腰三角形。
故答案为:√
【点睛】掌握圆锥的特征以及圆锥切割的特点是解题的关键。
18.180;0.2;1.9;60;
;300;;36
【解析】略
19.;10;
【分析】,同时算出两边小括号里的减法和除法,最后算括号外的除法,除以一个数等于乘这个数的倒数;
,利用乘法分配律进行简算,乘法分配律:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加;
,将百分数化成分数,逆用乘法分配律进行简算。
【详解】
20.x=25;x=16;x=0.4
【分析】,根据比例的基本性质,先写成的形式,两边同时÷即可;
,根据比例的基本性质,先写成的形式,两边同时÷即可;
,根据比例的基本性质,先写成的形式,两边同时÷4.6即可。
【详解】
解:
解:
解:
21.15.99dm2
【分析】两个半圆组合成一整个圆,侧面积等于整个圆柱的侧面积的一半,整个半圆柱的面积=整个圆柱的侧面积的一半+圆的面积+长方形的面积。
【详解】
(dm2)
22.17道
【分析】假设所有题全部做对,则分数是20×5=100(分)。与实际相差:100-79=21(分)。每做错一道题相差的分数:5+2=7(分),所以做错题数是21÷7=3(道),用做题总数量减去错题数量,求出做对题数量。
【详解】(20×5-79)÷(5+2)
=(100-79)÷7
=21÷7
=3(道)
20-3=17(道)
答:他做对了17道题。
23.6400件
【分析】把一月份生产服装的件数看作单位“1”,已知三月份生产服装8000件,比一月份增产25%,则三月份生产服装的件数是一月份的(1+25%),单位“1”未知,用三月份生产服装的件数除以(1+25%),即可求出一月份生产服装的件数。
【详解】8000÷(1+25%)
=8000÷1.25
=6400(件)
答:一月份生产服装6400件。
24.3分米
【分析】已知圆柱体的容积和底面积,根据高=圆柱体积÷底面积代入数据求出高,再乘即可。
【详解】
=
=3(分米)
答:油桶内油高为3分米。
25.80束
【分析】把这批花束的总数看作单位“1”,第一周、第二周分别完成了计划的、30%,那么第二周比第一周多生产的数量占总数的(30%-),单位“1”未知,用多生产的数量除以(30%-),即可求出这批花束的总数。
【详解】4÷(30%-)
=4÷(0.3-0.25)
=4÷0.05
=80(束)
答:花店计划生产花束80束。
26.(1)见详解
(2)①10% ②50 ③15
【分析】(1)通过统计图可知,参加足球运动的人数是10人,占全班人数的20%,用10÷20%即可求出全班的人数,把全班人数看作单位“1”也就是100%,用1-40%-30%-20%=10%即为乒乓球所占的比重。用全班人数乘对应的百分率即可求出参加其他体育运动的人数,然后完成统计图即可。
(2)①把全班人数看作单位“1”也就是100%,用1-40%-30%-20%=10%即为乒乓球所占的比重。
②参加足球运动的人数是10人,占全班人数的20%,用10÷20%即可求出全班的人数。
③分别求出踢毽球的学生人数和打乒乓球的人数,然后相减即可。
【详解】(1)1-40%-30%-20%
=60%-30%-20%
=30%-20%
=10%
全班人数:10÷20%=50(人)
毽球:50×40%=20(人),乒乓球:50×10%=5(人),其他:50×30%=15(人)
(2)①打乒乓球的学生占全班学生人数的10%;
②六(1)班学生共有50人。
③50×40%-50×10%
=20-5
=15(人)
踢毽球的学生人数比打乒乓球的人数多15人。
【点睛】本题考查已知一个数的百分之几是多少,求这个数,明确用除法是解题关键。
答案第1页,共2页
答案第1页,共2页
一、选择题
1.在下面各比中,能组成比例的是( )。
A.4∶3和∶3 B.3∶4和∶ C.3∶4和∶3 D.4∶3和∶
2.下面两种相关联的量成反比例的是( )。
A.互为倒数关系的A和B B.圆柱的高一定,它的体积和底面积
C.被减数一定,减数与差 D.长方形的宽一定,它的长和面积
3.“争创文明城,共建新枣庄”,六、2班有15人参加创城志愿者服务,比六、1班志愿者人数少4人,以下问题能用算式(15+4)÷15解决的是( )。
A.六、1班志愿者人数是六、2班志愿者人数的百分之几?
B.六、2班志愿者人数是六、1班志愿者人数的百分之几?
C.六、1班志愿者人数比六、2班志愿者人数多百分之几?
D.六、2班志愿者人数比六、1班志愿者人数少百分之几?
4.把一个棱长4分米的正方体木块削成一个最大的圆柱体,体积是( )立方分米。
A.200.96 B.100.48 C.64 D.50.24
5.一种商品先提价20%,再打八折,现价与原价相比,( )。
A.比原价高 B.比原价低 C.与原价相等 D.无法比较
6.我国逐渐完善养老金制度,居民可自行缴纳养老金。甲、乙两人计划用相同的年数分别缴纳养老金18万元和12万元。甲计划每年比乙多缴纳保险金0.2万元。若乙每年缴纳保险金x万元,则根据题意可列出比例为( )。
A. B.
C. D.
二、填空题
7.0.6=( )%=( )成=( )÷( )。
8.一支钢笔,打八折卖出亏10元,打九折卖出赚15元,则这件商品的标价是( )元,若卖218元,可赚( )元。
9.明明把2000元钱存入银行,定期两年,年利率是2.25%,到期后一共可以取回( )元。
10.如表中,如果x和y成正比例,空格里的数是( );如果x和y成反比例,空格里的数是( )。
y 2.4 6
x 10
11.把一段圆柱体木材料削成一个最大的圆锥,削去部分的体积是16立方厘米,这个圆锥的体积是( )立方厘米。
12.一个圆柱和圆锥的底面半径和高分别相等,已知圆锥体积比圆柱的体积少16立方米,圆柱的体积( )立方米,圆柱的体积比圆锥的体积多( )%。
三、判断题
13.如果a∶b=,那么4a=3b。( )
14.一件商品,降价20元后卖180元,这件商品折扣是八折。( )
15.在一个比例中,两个外项的积减去两个内项的积,差为0。( )
16.有一个圆柱的底面直径和高相等,它的侧面可以展开成一个正方形。( )
17.从圆锥的顶点沿高切成两部分,得到的截面一定是等腰三角形。( )
四、计算题
18.直接写得数。
19.计算下面各题。
20.解比例。
21.求下图中半圆柱的表面积。
五、解答题
22.一张数学试卷中共有20道题,做对一个得5分,做错一题扣2分。王亮做了全部的题目,共得79分,他做对几道题?
23.某服装厂三月份生产服装8000件,比一月份增产25%,一月份生产服装多少件?
24.一个圆柱形油桶的容积是48立方分米,内底面积是12平方分米,装了桶油。油桶内油高多少分米?
25.母亲节快到了,花店计划用两周的时间完成一批花束的生产任务。第一周完成了计划的,第二周完成了计划的30%,正好比第一周多生产4束,花店计划生产花束多少束?
26.新冠肺炎疫情时期,为了更好地提高学生免疫力,某小学开展形式多样的“阳光体育运动”活动,淘气对六(1)班学生参加体育锻炼类型的情况进行统计,并分别绘制成下面的两种统计图(见图1和图2)。
(1)请将图1、图2补充完整。
(2)请根据图中提供的信息,完成下列填空:
①打乒乓球的学生占全班学生人数的__________;
②六(1)班学生共有__________人;
③踢毽球的学生人数比打乒乓球的人数多__________人。
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】判断两个比能不能组成比例,可以分别求出比值,比值相等,能组成比例,否则,不能组成比例,据此解答。
【详解】A.4∶3
=4÷3
=
∶3
=÷3
=×
=
≠,所以4∶3和∶3不能组成比例;
B.3∶4
=3÷4
=
∶
=÷
=×3
=
=,所以3∶4=∶,能组成比例;
C.3∶4
=3÷4
=
∶3
=÷3
=×
=
≠,所以3∶4和∶3不能组成比例;
D.4∶3
=4÷3
=
∶
=÷
=×3
=
≠,所以4∶3和∶不能组成比例;
故答案为:B
2.A
【分析】两种相关联的量,若两种量的比值一定,两种量成正比例;若两种量的乘积一定,两种量成反比例;若两种量既不存在比值一定,又不存在乘积一定,两种量不成比例。据此解答。
【详解】A.A和B互为倒数,则AB=1,A和B的乘积一定,A和B成反比例;
B.圆柱的高=体积÷底面积,圆柱的高一定时,它的体积和底面积成正比例;
C.被减数=减数+差,被减数一定时,减数与差不成比例;
D.长方形的宽=面积÷长,长方形的宽一定时,它的长和面积成正比例。
故答案为:A
【点睛】辨识两种相关联的量成正比例还是成反比例,就看这两种量是比值一定,还是乘积一定。
3.A
【分析】根据题意可知,(15+4)求的是六、1班志愿者的人数,是被除数;除数15是六、2班的人数,把15看作单位“1”,所以此算式求的是六、1班志愿者人数是六、2班志愿者人数的百分之几据此即可解答。
【详解】能用算式(15+4)÷15解决的是六、1班志愿者人数是六、2班志愿者人数的百分之几?
故答案为:A
【点睛】本题是求一个数是另一个数的百分之几,关键是看把谁当成了单位“1”,单位“1”的量为除数。
4.D
【分析】正方体内削出的最大圆柱的底面直径和高都等于这个正方体的棱长,由此利用圆柱的体积公式:,即可解答。
【详解】3.14×(4÷2)2×4
=3.14×4×4
=50.24(立方分米)
故答案为:D
5.B
【分析】假设这种商品的价格1,并把它看成单位“1”,提高后的价格是原价的(1+20%),由此用乘法求出提高后的价格;
再把提高后的价格看成单位“1”,再打八折出售即现价是提高后价格的80%,由此用乘法求出现价,再比较原价和现价即可。
【详解】假设原价是1;
1×(1+20%)×80%
=1×120%×80%
=0.96
1>0.96
现价比原价低。
故答案为:B
6.B
【分析】设乙每年缴纳养老保险为x万元,则甲每年缴纳养老保险金为(x+0.2)万元,根据甲、乙两人计划用相同的年数分别缴纳养老保险金18万元和12万元可知,18比上(x+0.2)万元等于12比上x万元。
【详解】根据题意可列出比例为。
故答案为:B
7.21;60;六;3;5
【分析】分数的分子相当于被除数,分母相当于除数,分数的分子和分母,同时乘或除以相同的数(0除外),分数的大小不变。据此先将小数化成分数,根据分数与除法的关系,以及它们通用的基本性质进行填空,小数化百分数,小数点向右移动两位,添上百分号即可,根据几成就是百分之几十,确定成数。
【详解】0.6==3÷5,35÷5×3=21;0.6=60%=六成
0.6=60%=六成=3÷5
8. 250 8
【分析】由题意可知,标价的80%加上10,与标价的90%减去15都表示钢笔的进价。根据这一数量关系求商品的标价,可以列方程解答。然后用标价乘80%再加10求出进价,最后用218减去进价,可算出赚了多少钱。据此解答。
【详解】解:设钢笔的标价为x元。
90%x-15=80%x+10
0.9x-0.8x=15+10
0.1x=25
x=250
218-(250×80%+10)
=218-(200+10)
=218-210
=8(元)
所以,这件商品的标价是250元,若卖218元,可赚8元。
9.2090
【分析】取回的钱包括本金和利息,利息=本金×利率×存期,本金+利息=可以取回的钱,据此列式计算。
【详解】2000+2000×2.25%×2
=2000+2000×0.0225×2
=2000+90
=2090(元)
到期后一共可以取回2090元。
10. 4 25
【分析】因为x和y成正比例,所以y∶x是定值,而y∶x=6∶10=0.6,由此求出x的值;因为x和y成反比例,所以x与y的乘积是定值,而xy=6×10=60,由此求出x的值。
【详解】y∶x
=6∶10
=0.6
所以x=2.4÷0.6=4;
因为xy=6×10=60,所以x=60÷2.4=25。
11.8
【分析】圆柱内最大的圆锥与原来圆柱是等底等高的,所以圆锥的体积是圆柱的体积是的,则圆锥的体积就是削去部分的体积的,由此即可解答。
【详解】16×=8(立方厘米)
这个圆锥的体积是8立方厘米。
12. 24 200
【分析】等底等高的圆锥的体积是圆柱的,所以这里的体积之差就是圆柱的,由此可得圆柱的体积就是16÷=24(立方厘米),再用圆柱体积与圆锥体积的差除以圆锥的体积,计算圆柱比圆锥体积多百分之几即可。
【详解】16÷(1-)
=16÷
=24(立方厘米)
24×=8(立方米)
(24-8)÷8
=16÷8
=200%
圆柱的体积是(24)立方厘米,圆柱的体积比圆锥的体积多(200)%。
13.√
【分析】将分数写成比的形式,根据比例的基本性质,比例的两内项积=两外项积,进行分析。
【详解】=3∶4,a∶b=3∶4,根据比例的基本性质,可得4a=3b,原题说法正确。
故答案为:√
14.×
【分析】先求出原价,降价后价格÷原价=现价是原价的百分之几,根据几折就是百分之几十,确定折数。
【详解】180÷(180+20)
=180÷200
=0.9
=90%
一件商品,降价20元后卖180元,这件商品折扣是九折,原题说法错误。
故答案为:×
15.√
【分析】比例的基本性质:在比例里,两个外项的积等于两个内项的积。
【详解】在一个比例中,两个外项的积等于两个内项的积,所以两个外项的积减去两个内项的积,差为0。
原题说法正确。
故答案为:√
16.×
【分析】圆柱侧面展开图是个正方形,说明圆柱底面周长=圆柱的高,据此分析。
【详解】有一个圆柱的底面直径和高相等,沿着直径切开的剖面是个正方形,侧面展开是个长方形,原题说法错误。
故答案为:×
【点睛】关键是熟悉圆柱特征,理解圆柱侧面展开图和圆柱之间的关系。
17.√
【分析】根据圆锥的特征,圆锥沿高切成两部分,切面是以底面直径为底、以圆锥的高为高的等腰三角形。
【详解】
如图所示:从圆锥的顶点沿高切成两部分,得到的截面是等腰三角形。
故答案为:√
【点睛】掌握圆锥的特征以及圆锥切割的特点是解题的关键。
18.180;0.2;1.9;60;
;300;;36
【解析】略
19.;10;
【分析】,同时算出两边小括号里的减法和除法,最后算括号外的除法,除以一个数等于乘这个数的倒数;
,利用乘法分配律进行简算,乘法分配律:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加;
,将百分数化成分数,逆用乘法分配律进行简算。
【详解】
20.x=25;x=16;x=0.4
【分析】,根据比例的基本性质,先写成的形式,两边同时÷即可;
,根据比例的基本性质,先写成的形式,两边同时÷即可;
,根据比例的基本性质,先写成的形式,两边同时÷4.6即可。
【详解】
解:
解:
解:
21.15.99dm2
【分析】两个半圆组合成一整个圆,侧面积等于整个圆柱的侧面积的一半,整个半圆柱的面积=整个圆柱的侧面积的一半+圆的面积+长方形的面积。
【详解】
(dm2)
22.17道
【分析】假设所有题全部做对,则分数是20×5=100(分)。与实际相差:100-79=21(分)。每做错一道题相差的分数:5+2=7(分),所以做错题数是21÷7=3(道),用做题总数量减去错题数量,求出做对题数量。
【详解】(20×5-79)÷(5+2)
=(100-79)÷7
=21÷7
=3(道)
20-3=17(道)
答:他做对了17道题。
23.6400件
【分析】把一月份生产服装的件数看作单位“1”,已知三月份生产服装8000件,比一月份增产25%,则三月份生产服装的件数是一月份的(1+25%),单位“1”未知,用三月份生产服装的件数除以(1+25%),即可求出一月份生产服装的件数。
【详解】8000÷(1+25%)
=8000÷1.25
=6400(件)
答:一月份生产服装6400件。
24.3分米
【分析】已知圆柱体的容积和底面积,根据高=圆柱体积÷底面积代入数据求出高,再乘即可。
【详解】
=
=3(分米)
答:油桶内油高为3分米。
25.80束
【分析】把这批花束的总数看作单位“1”,第一周、第二周分别完成了计划的、30%,那么第二周比第一周多生产的数量占总数的(30%-),单位“1”未知,用多生产的数量除以(30%-),即可求出这批花束的总数。
【详解】4÷(30%-)
=4÷(0.3-0.25)
=4÷0.05
=80(束)
答:花店计划生产花束80束。
26.(1)见详解
(2)①10% ②50 ③15
【分析】(1)通过统计图可知,参加足球运动的人数是10人,占全班人数的20%,用10÷20%即可求出全班的人数,把全班人数看作单位“1”也就是100%,用1-40%-30%-20%=10%即为乒乓球所占的比重。用全班人数乘对应的百分率即可求出参加其他体育运动的人数,然后完成统计图即可。
(2)①把全班人数看作单位“1”也就是100%,用1-40%-30%-20%=10%即为乒乓球所占的比重。
②参加足球运动的人数是10人,占全班人数的20%,用10÷20%即可求出全班的人数。
③分别求出踢毽球的学生人数和打乒乓球的人数,然后相减即可。
【详解】(1)1-40%-30%-20%
=60%-30%-20%
=30%-20%
=10%
全班人数:10÷20%=50(人)
毽球:50×40%=20(人),乒乓球:50×10%=5(人),其他:50×30%=15(人)
(2)①打乒乓球的学生占全班学生人数的10%;
②六(1)班学生共有50人。
③50×40%-50×10%
=20-5
=15(人)
踢毽球的学生人数比打乒乓球的人数多15人。
【点睛】本题考查已知一个数的百分之几是多少,求这个数,明确用除法是解题关键。
答案第1页,共2页
答案第1页,共2页
同课章节目录
