第一讲不等式和绝对值不等式(一)
文档属性
| 名称 | 第一讲不等式和绝对值不等式(一) |

|
|
| 格式 | rar | ||
| 文件大小 | 591.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-18 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
思考一
重要不等式的应用举例
引入
重要不等式的推广
练习
下面我们来系统且更进一步地认识不等式,从而进一步提高分析问题、处理问题的能力。
这一结论虽很简单,却是我们推导或证明不等式的基础.
不等式的基本性质
基本不等式
解不等式的过程就是对不等式进行一系列同解变形的过程,同解变形的依据是什么?
证明不等式的最基本的思考是分析法——很多时候就是对要证的不等式进行变形转化。
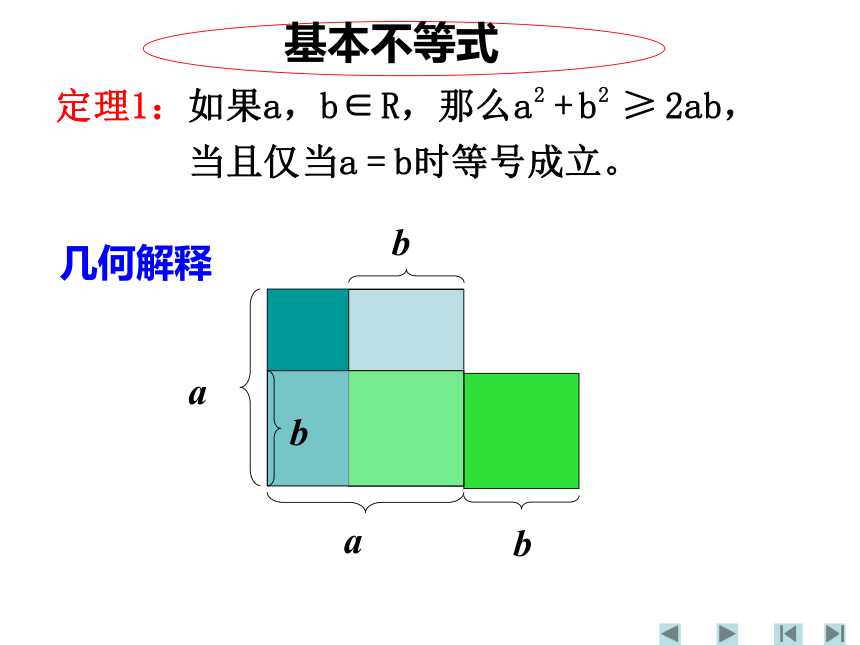
基本不等式
a
a
b
b
b
几何解释
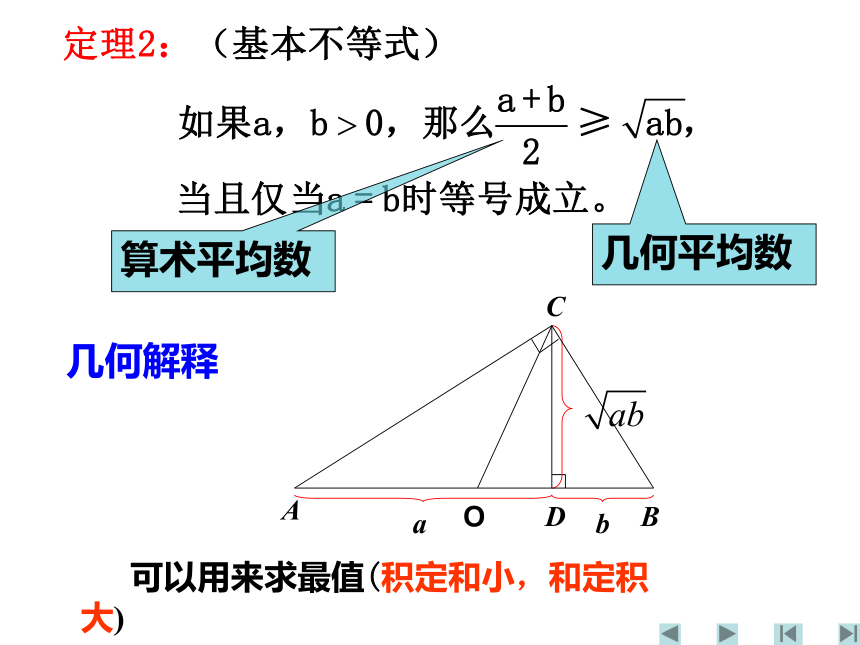
几何平均数 (a 、b 的)
算术平均数(a 、b 的)
算术平均数
几何平均数
几何解释
O
a
b
D
A
C
B
可以用来求最值(积定和小,和定积大)
例3答案
例4
例 3求证:(1)在所有周长相同的矩形中,正方 --------------形的面积最大;
(2)在所有面积相同的矩形中,正方 ---------------形的周长最短.
例 3求证:(1)在所有周长相同的矩形中,正方 --------------形的面积最大;
(2)在所有面积相同的矩形中,正方 ---------------形的周长最短.
x
y
S
周长L=2x+2y
设矩形周长为L,面积为S,一边长为x,一边长为y,
例4: 某居民小区要建一做八边形的休闲场所,它的主体造型平面图是由两个相同的矩形ABCD和EFGH构成的面积为200平方米的十字型地域.计划在正方形MNPQ上建一座花坛,造价为每平方米4300元,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价没平方米210元,再在四个空角(图中四个三角形)上铺草坪,每平方米造价80元. (1)设总造价为S元,AD长 x 为米,试建立S关于x的函数关系式; (2)当为何值时S最小, 并求出这个最小值.
Q
D
B
C
F
A
E
H
G
P
M
N
解:设AM=y米
2答案
3答案
四:三个正数的算术—几何平均不等式
类比基本不等式得
例1 求函数 在 上的最大值.
问题 求证:在表面积一定的长方体中,以正方体的体积最大.
x
y
z
解:设长方体的三边长度分别为x、y、z,则长方体的体积为
而
略
例2: 如图,把一块边长是a 的正方形铁 片的各角切 去大小相同的小正方形, 再把它的边沿着虚线折转作成一个无盖方底的盒子,问切去的正方形边长是多小时?才能使盒子的容积最大?
a
x
题
试证明:已知a、b、c∈R+,
求证
求证:
思考一
重要不等式的应用举例
引入
重要不等式的推广
练习
下面我们来系统且更进一步地认识不等式,从而进一步提高分析问题、处理问题的能力。
这一结论虽很简单,却是我们推导或证明不等式的基础.
不等式的基本性质
基本不等式
解不等式的过程就是对不等式进行一系列同解变形的过程,同解变形的依据是什么?
证明不等式的最基本的思考是分析法——很多时候就是对要证的不等式进行变形转化。
基本不等式
a
a
b
b
b
几何解释
几何平均数 (a 、b 的)
算术平均数(a 、b 的)
算术平均数
几何平均数
几何解释
O
a
b
D
A
C
B
可以用来求最值(积定和小,和定积大)
例3答案
例4
例 3求证:(1)在所有周长相同的矩形中,正方 --------------形的面积最大;
(2)在所有面积相同的矩形中,正方 ---------------形的周长最短.
例 3求证:(1)在所有周长相同的矩形中,正方 --------------形的面积最大;
(2)在所有面积相同的矩形中,正方 ---------------形的周长最短.
x
y
S
周长L=2x+2y
设矩形周长为L,面积为S,一边长为x,一边长为y,
例4: 某居民小区要建一做八边形的休闲场所,它的主体造型平面图是由两个相同的矩形ABCD和EFGH构成的面积为200平方米的十字型地域.计划在正方形MNPQ上建一座花坛,造价为每平方米4300元,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价没平方米210元,再在四个空角(图中四个三角形)上铺草坪,每平方米造价80元. (1)设总造价为S元,AD长 x 为米,试建立S关于x的函数关系式; (2)当为何值时S最小, 并求出这个最小值.
Q
D
B
C
F
A
E
H
G
P
M
N
解:设AM=y米
2答案
3答案
四:三个正数的算术—几何平均不等式
类比基本不等式得
例1 求函数 在 上的最大值.
问题 求证:在表面积一定的长方体中,以正方体的体积最大.
x
y
z
解:设长方体的三边长度分别为x、y、z,则长方体的体积为
而
略
例2: 如图,把一块边长是a 的正方形铁 片的各角切 去大小相同的小正方形, 再把它的边沿着虚线折转作成一个无盖方底的盒子,问切去的正方形边长是多小时?才能使盒子的容积最大?
a
x
题
试证明:已知a、b、c∈R+,
求证
求证:
