3.1 勾股定理 同步测试卷(无答案) 苏科版八年级数学上册
文档属性
| 名称 | 3.1 勾股定理 同步测试卷(无答案) 苏科版八年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 252.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-11 00:00:00 | ||
图片预览

文档简介
3.1 勾股定理 同步测试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共8小题,共24分。在每小题列出的选项中,选出符合题目的一项)
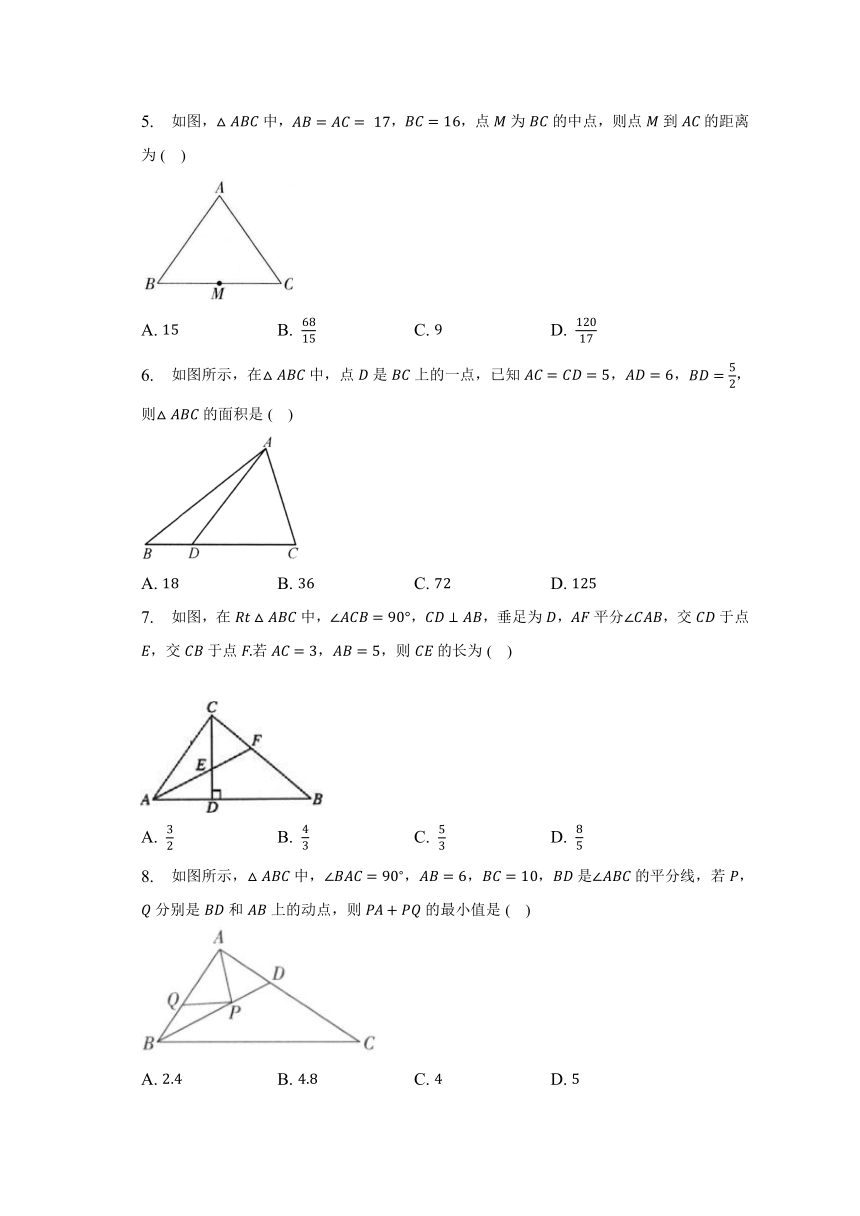
1. 在中,,,,则的长为( )
A. B. C. D.
2. 勾股定理是人类最伟大的科学发现之一,在我国古算书周髀算经中早有记载如图,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图的方式放置在最大正方形内,则图中阴影部分的面积等于( )
A. 直角三角形的面积 B. 最大正方形的面积
C. 较小两个正方形重叠部分的面积 D. 最大正方形与直角三角形的面积和
3. 如图,在中,于点,,,,则的长为( )
A. B. C. D.
4. 如图,有一张直角三角形纸片,两条直角边,,将折叠,使点和点重合,折痕为,则的长为 ( )
A. B. C. D.
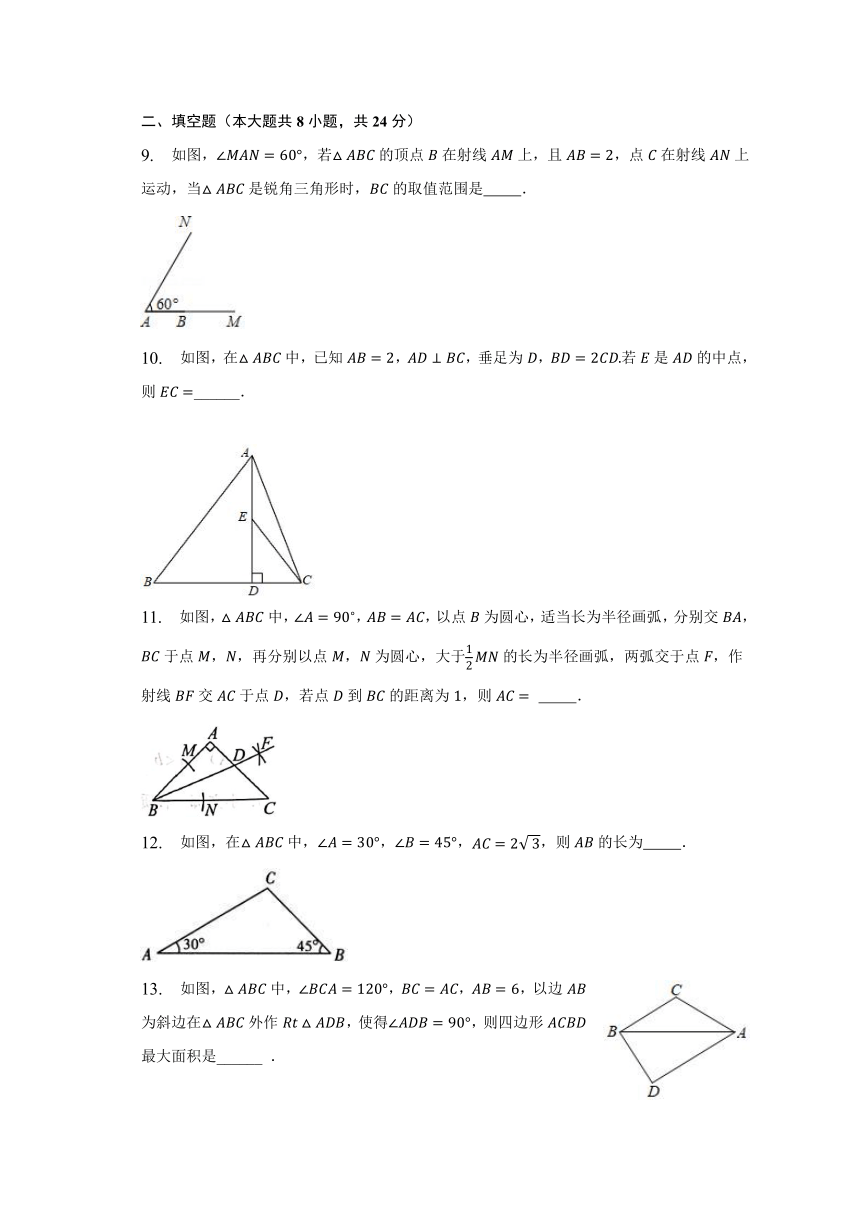
5. 如图,中,,,点为的中点,则点到的距离为( )
A. B. C. D.
6. 如图所示,在中,点是上的一点,已知,,,则的面积是( )
A. B. C. D.
7. 如图,在中,,,垂足为,平分,交于点,交于点若,,则的长为( )
A. B. C. D.
8. 如图所示,中,,,,是的平分线,若,分别是和上的动点,则的最小值是( )
A. B. C. D.
二、填空题(本大题共8小题,共24分)
9. 如图,,若的顶点在射线上,且,点在射线上运动,当是锐角三角形时,的取值范围是 .
10. 如图,在中,已知,,垂足为,若是的中点,则______.
11. 如图,中,,,以点为圆心,适当长为半径画弧,分别交,于点,,再分别以点,为圆心,大于的长为半径画弧,两弧交于点,作射线交于点,若点到的距离为,则 .
12. 如图,在中,,,,则的长为 .
13. 如图,中,,,,以边为斜边在外作,使得,则四边形最大面积是______ .
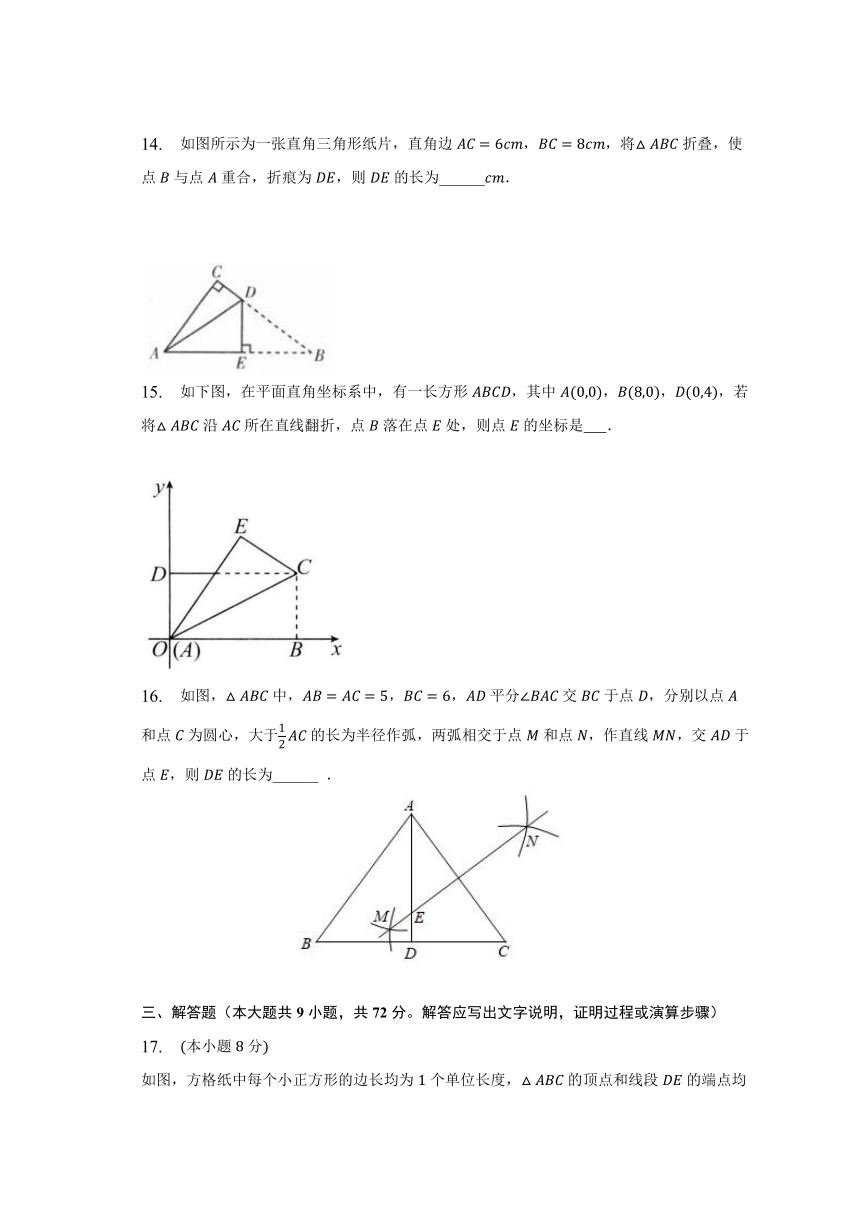
14. 如图所示为一张直角三角形纸片,直角边,,将折叠,使点与点重合,折痕为,则的长为______.
15. 如下图,在平面直角坐标系中,有一长方形,其中,,,若将沿所在直线翻折,点落在点处,则点的坐标是 .
16. 如图,中,,,平分交于点,分别以点和点为圆心,大于的长为半径作弧,两弧相交于点和点,作直线,交于点,则的长为______ .
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
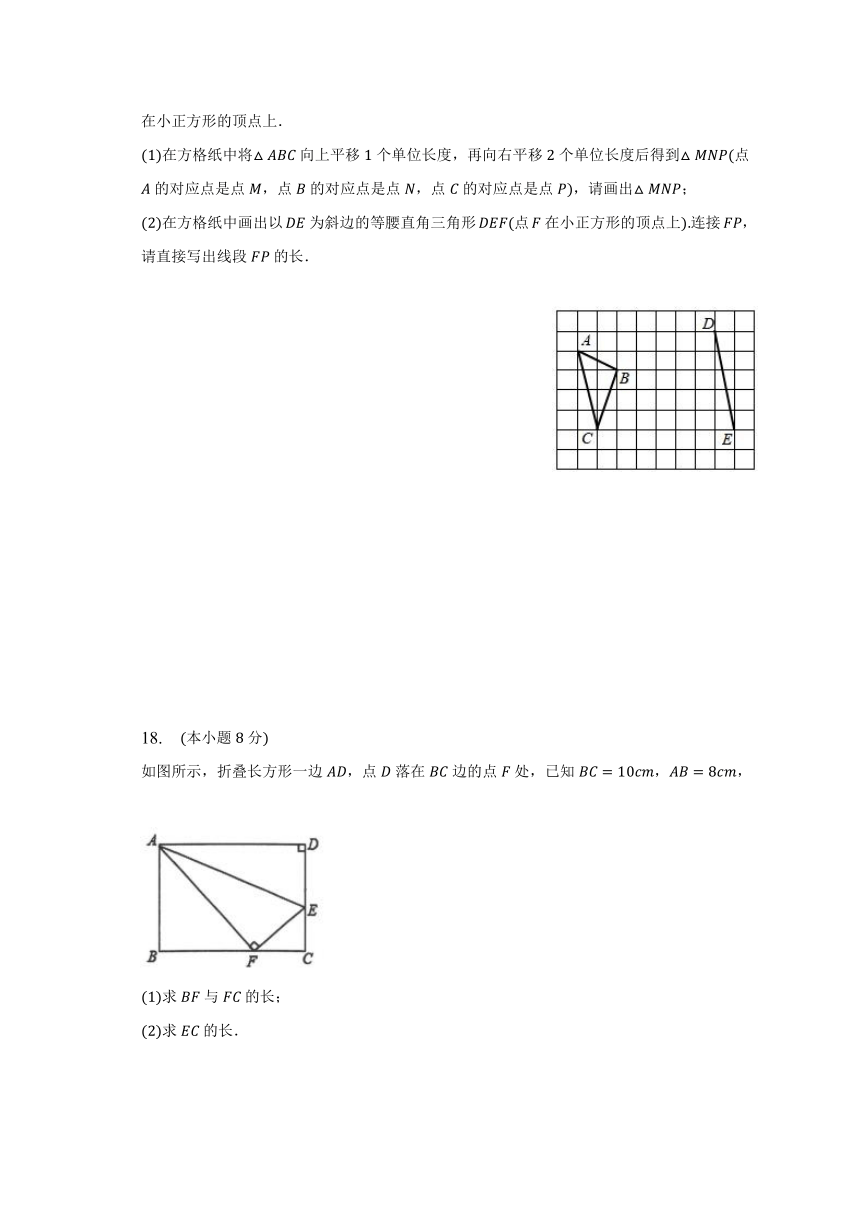
如图,方格纸中每个小正方形的边长均为个单位长度,的顶点和线段的端点均在小正方形的顶点上.
在方格纸中将向上平移个单位长度,再向右平移个单位长度后得到点的对应点是点,点的对应点是点,点的对应点是点,请画出;
在方格纸中画出以为斜边的等腰直角三角形点在小正方形的顶点上连接,请直接写出线段的长.
18. 本小题分
如图所示,折叠长方形一边,点落在边的点处,已知,,
求与的长;
求的长.
19. 本小题分
一块等腰直角三角尺按照如图所示方式放置.直角顶点在直线上,分别过点,作直线于点,直线于点.
求证:.
若设三边分别为,,,利用此图证明勾股定理.
20. 本小题分
如图,在长方形中,,.
若是边上的一个动点,当点在什么位置时,?
在第题中,当点在点时,有,是边上的一个动点.当时,与垂直吗?为什么?
21. 本小题分
如图,在中,,,,求的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路,完成解答过程.
作于点,设,用含的代数式表示,则________.
请根据勾股定理,利用作为“桥梁”建立方程,并求出的值.
利用勾股定理求出的长,再计算三角形的面积.
22. 本小题分
求下列直角三角形中未知的边长.
23. 本小题分
如图,在中,,,,求斜边的长.
24. 本小题分
勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪灵感他惊喜地发现,当两个全等的直角三角形按如图所示的方式摆放时,都可以用“面积法”来证明勾股定理下面是小聪利用图证明勾股定理的过程:
将两个全等的直角三角形按如图所示的方式摆放,其中求证:.
证明:连接,过点作边上的高,交的延长线于点,则.
,
又,
.
.
请参照上述证法,利用图完成下面的证明.
将两个全等的直角三角形按如图所示的方式摆放,其中.
求证:.
证明:连接 .
,
又 ,
.
.
25. 本小题分
如图,在中,,,,若点从点出发,以每秒的速度沿折线运动,设运动时间为秒.
若点在上,且满足时,求出此时的值;
若点恰好在的角平分线上,求的值;
在运动过程中,直接写出当为何值时,为等腰三角形.
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共8小题,共24分。在每小题列出的选项中,选出符合题目的一项)
1. 在中,,,,则的长为( )
A. B. C. D.
2. 勾股定理是人类最伟大的科学发现之一,在我国古算书周髀算经中早有记载如图,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图的方式放置在最大正方形内,则图中阴影部分的面积等于( )
A. 直角三角形的面积 B. 最大正方形的面积
C. 较小两个正方形重叠部分的面积 D. 最大正方形与直角三角形的面积和
3. 如图,在中,于点,,,,则的长为( )
A. B. C. D.
4. 如图,有一张直角三角形纸片,两条直角边,,将折叠,使点和点重合,折痕为,则的长为 ( )
A. B. C. D.
5. 如图,中,,,点为的中点,则点到的距离为( )
A. B. C. D.
6. 如图所示,在中,点是上的一点,已知,,,则的面积是( )
A. B. C. D.
7. 如图,在中,,,垂足为,平分,交于点,交于点若,,则的长为( )
A. B. C. D.
8. 如图所示,中,,,,是的平分线,若,分别是和上的动点,则的最小值是( )
A. B. C. D.
二、填空题(本大题共8小题,共24分)
9. 如图,,若的顶点在射线上,且,点在射线上运动,当是锐角三角形时,的取值范围是 .
10. 如图,在中,已知,,垂足为,若是的中点,则______.
11. 如图,中,,,以点为圆心,适当长为半径画弧,分别交,于点,,再分别以点,为圆心,大于的长为半径画弧,两弧交于点,作射线交于点,若点到的距离为,则 .
12. 如图,在中,,,,则的长为 .
13. 如图,中,,,,以边为斜边在外作,使得,则四边形最大面积是______ .
14. 如图所示为一张直角三角形纸片,直角边,,将折叠,使点与点重合,折痕为,则的长为______.
15. 如下图,在平面直角坐标系中,有一长方形,其中,,,若将沿所在直线翻折,点落在点处,则点的坐标是 .
16. 如图,中,,,平分交于点,分别以点和点为圆心,大于的长为半径作弧,两弧相交于点和点,作直线,交于点,则的长为______ .
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
如图,方格纸中每个小正方形的边长均为个单位长度,的顶点和线段的端点均在小正方形的顶点上.
在方格纸中将向上平移个单位长度,再向右平移个单位长度后得到点的对应点是点,点的对应点是点,点的对应点是点,请画出;
在方格纸中画出以为斜边的等腰直角三角形点在小正方形的顶点上连接,请直接写出线段的长.
18. 本小题分
如图所示,折叠长方形一边,点落在边的点处,已知,,
求与的长;
求的长.
19. 本小题分
一块等腰直角三角尺按照如图所示方式放置.直角顶点在直线上,分别过点,作直线于点,直线于点.
求证:.
若设三边分别为,,,利用此图证明勾股定理.
20. 本小题分
如图,在长方形中,,.
若是边上的一个动点,当点在什么位置时,?
在第题中,当点在点时,有,是边上的一个动点.当时,与垂直吗?为什么?
21. 本小题分
如图,在中,,,,求的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路,完成解答过程.
作于点,设,用含的代数式表示,则________.
请根据勾股定理,利用作为“桥梁”建立方程,并求出的值.
利用勾股定理求出的长,再计算三角形的面积.
22. 本小题分
求下列直角三角形中未知的边长.
23. 本小题分
如图,在中,,,,求斜边的长.
24. 本小题分
勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪灵感他惊喜地发现,当两个全等的直角三角形按如图所示的方式摆放时,都可以用“面积法”来证明勾股定理下面是小聪利用图证明勾股定理的过程:
将两个全等的直角三角形按如图所示的方式摆放,其中求证:.
证明:连接,过点作边上的高,交的延长线于点,则.
,
又,
.
.
请参照上述证法,利用图完成下面的证明.
将两个全等的直角三角形按如图所示的方式摆放,其中.
求证:.
证明:连接 .
,
又 ,
.
.
25. 本小题分
如图,在中,,,,若点从点出发,以每秒的速度沿折线运动,设运动时间为秒.
若点在上,且满足时,求出此时的值;
若点恰好在的角平分线上,求的值;
在运动过程中,直接写出当为何值时,为等腰三角形.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
