第一讲不等式和绝对值不等式(三)
文档属性
| 名称 | 第一讲不等式和绝对值不等式(三) |
|
|
| 格式 | rar | ||
| 文件大小 | 338.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-18 00:00:00 | ||
图片预览





文档简介
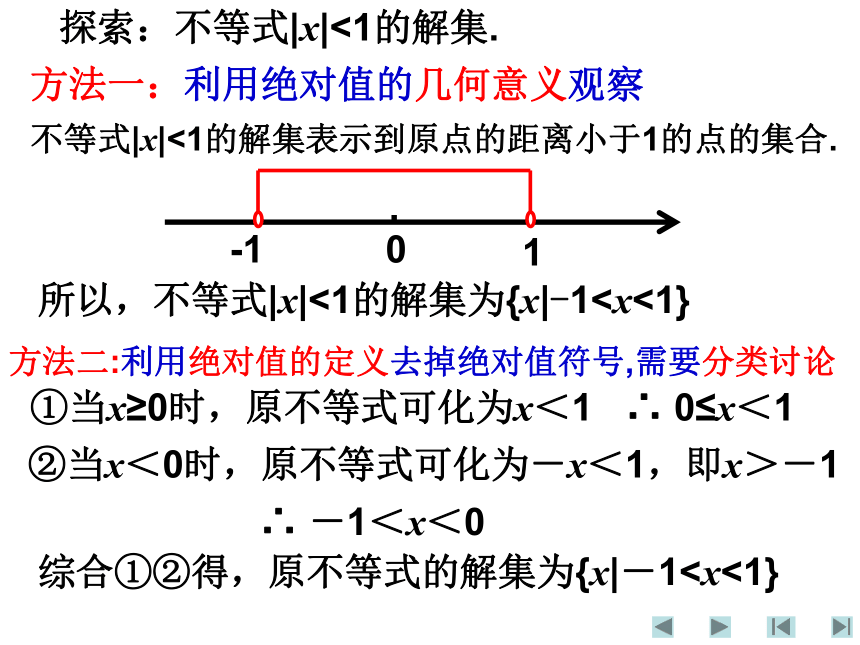
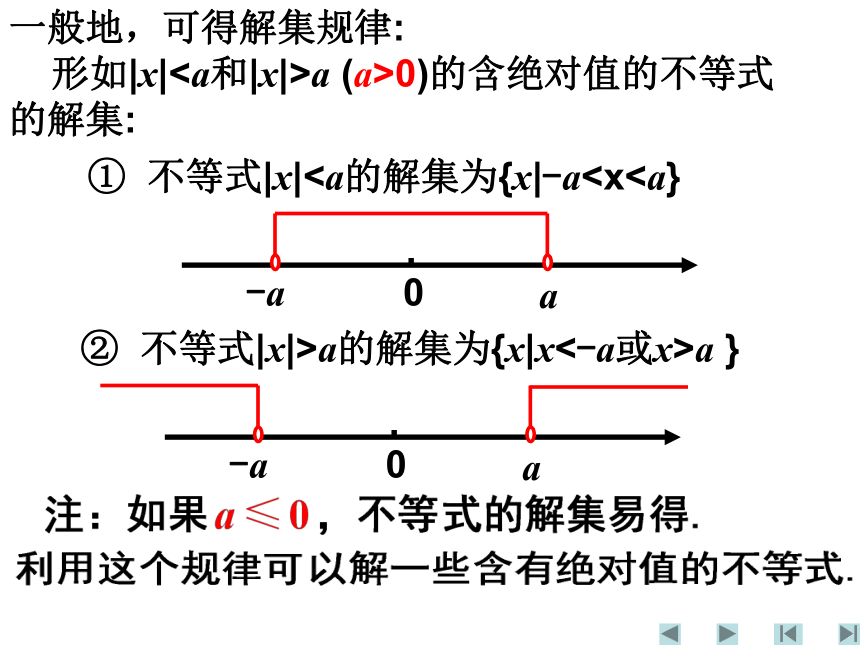
课件15张PPT。尝试练习一练习二问题引入解法公式本课小结补充练习方法一: 利用绝对值的几何意义观察;方法二: 利用绝对值的定义去掉绝对值符号,需要分类讨论;方法三: 两边同时平方去掉绝对值符号;方法四: 利用函数图象观察.这也是解其他含绝对值不等式的四种常用思路.主要方法有:0-1不等式|x|<1的解集表示到原点的距离小于1的点的集合.1所以,不等式|x|<1的解集为{x|-1 形如|x|a (a>0)的含绝对值的不等式的解集:① 不等式|x|a的解集为{x|x<-a或x>a }解法公式拓广挑战题试解下列不等式:课堂练习一:1答案2答案课堂练习二(挑战):2.试解不等式|x-1|+|x+2|≥5 解绝对值不等式关键是去绝对值符号,你有什么方法解决这个问题?还有没有其他方法?2.试解不等式|x-1|+|x+2|≥5方法一:利用绝对值的几何意义,体现了数形结合的思想.方法小结2.解不等式|x-1|+|x+2|≥5方法二:利用|x-1|=0,|x+2|=0的零点,将数轴分为三个区间,然后在这三个区间上将原不等式分别化为不含绝对值符号的不等式求解.体现了分类讨论的思想.2.解不等式|x-1|+|x+2|≥5方法三:通过构造函数,利用函数的图象,体现了函数与方程的思想.方法小结3.不等式 有解的条件是( )1.解不等式|2x-4|-|3x+9|<1B1.解不等式|2x-4|-|3x+9|<1解:10当x>2时,原不等式同解于x>230当x<-3时,原不等式同解于20当-3≤x≤2时,原不等式同解于x<-13综合上述知不等式的解集为
