高中数列复习讲义
图片预览




文档简介
学科教师辅导讲义
讲义编号:____________ 学生签名:
学员编号: 年 级: 课时数:2学员姓名: 辅导科目: 学科教师:
课 题
授课日期及时段
教学内容
教学内容
数列概念1.数列的定义:按照一定顺序排列的一列数称为数列,数列中的每个数称为该数列的项.2.通项公式:如果数列的第项与序号之间可以用一个式子表示,那么这个公式叫做这个数列的通项公式,即. 3.递推公式:如果已知数列的第一项(或前几项),且任何一项与它的前一项(或前几项)间的关系可以用一个式子来表示,即或,那么这个式子叫做数列的递推公式. 如数列中,,其中是数列的递推公式.4.数列的前项和与通项的公式①; ②.5. 数列的表示方法:解析法、图像法、列举法、递推法.6. 数列的分类:有穷数列,无穷数列;递增数列,递减数列,摆动数列,常数数列;有界数列,无界数列.①递增数列:对于任何,均有.②递减数列:对于任何,均有.③摆动数列:例如: ④常数数列:例如:6,6,6,6,…….⑤有界数列:存在正数使.⑥无界数列:对于任何正数,总有项使得. 等差数列1.等差数列的概念如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,这个数列叫做等差数列,常数称为等差数列的公差. 2.通项公式与前项和公式⑴通项公式,为首项,为公差.⑵前项和公式或.3.等差中项如果成等差数列,那么叫做与的等差中项.即:是与的等差中项,,成等差数列.4.等差数列的判定方法⑴定义法:(,是常数)是等差数列;⑵中项法:()是等差数列.5.等差数列的常用性质⑴数列是等差数列,则数列、(是常数)都是等差数列;⑵在等差数列中,等距离取出若干项也构成一个等差数列,即为等差数列,公差为.⑶;(,是常数);(,是常数,)⑷若,则;⑸若等差数列的前项和,则是等差数列;⑹当项数为,则; 当项数为,则.等比数列1.等比数列的概念如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,这个数列叫做等比数列,常数称为等比数列的公比. 2.通项公式与前项和公式⑴通项公式:,为首项,为公比 .⑵前项和公式:①当时,②当时,.3.等比中项如果成等比数列,那么叫做与的等比中项.即:是与的等差中项,,成等差数列.4.等比数列的判定方法⑴定义法:(,是常数)是等比数列;⑵中项法:()且是等比数列.5.等比数列的常用性质⑴数列是等比数列,则数列、(是常数)都是等比数列;⑵在等比数列中,等距离取出若干项也构成一个等比数列,即为等比数列,公比为.⑶⑷若,则;⑸若等比数列的前项和,则、、、是等比数列.二、典型例题A、求值类的计算题(多关于等差等比数列)1)根据基本量求解(方程的思想)1、已知为等差数列的前项和,,求;
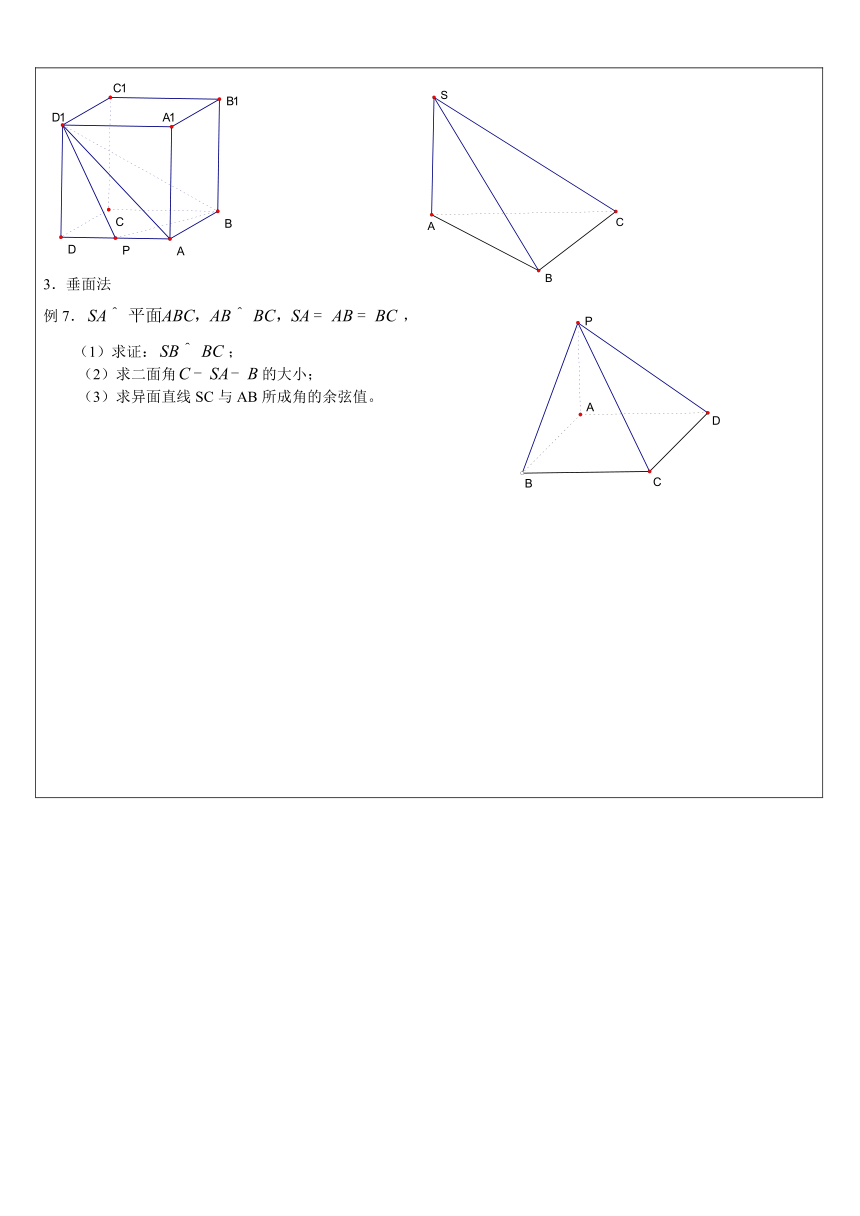
2、等差数列 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )中,且成等 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )比数列,求数列前20项的和.3、设是公比为正数的等比数列,若,求数列前7项的和.4、已知四个实数,前三个数成等差数列,后三个数成等比数列,首末两数之和为,中间两数之和为,求这四个数.2)根据数列的性质求解(整体思想)1、已知为等差数列的前项和,,则 ;2、设、分别是等差数列、的前项和,,则 .3、设是等差数列的前n项和,若( )4、等差数列,的前项和分别为,,若,则=( )5、已知为等差数列的前项和,,则 .6、在正项等比数列中,,则_______。7、已知数列是等差数列,若 ,且,则_________。8、已知为等比数列前项和,,,则 .9、在等差数列中,若,则的值为( )10、在等比数列中,已知,,则 . 11、已知为等差数列,,则 12、等差数列中,已知一、平面与平面的垂直关系1.判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。例1.在空间四边形ABCD中,AB=CB,AD=CD,E、F、G分别是AD、DC、CA的中点。 求证:。例2.,,E、F分别是AC、AD的中点。 求证: 。2.性质定理:若两个平面互相垂直,则在一个平面内垂直于它们交线的直线垂直于另一个平面。例3.在正方体ABCD—A1B1C1D1中,求A1B和平面A1B1CD所成的角.。二、二面角的基本求法1.定义法:在棱上取点,分别在两面内引两条射线与棱垂直。例4.在正方体ABCD—A1B1C1D1中, 求(1)二面角的大小; (2)平面与平面所成角的正切值。练习:过正方形ABCD的顶点A作,设PA=AB=,求二面角的大小。2.三垂线法例5.是正方形,ABEF是矩形且AF=AD=,G是EF的中点,(1)求证:;(2)求GB与平面AGC所成角的正弦值;(3)求二面角的大小。例6.点P在平面ABC外,是等腰直角三角形,,是正三角形,。(1)求证:;(2)求二面角的大小。练习:正方体ABCD—A1B1C1D1的棱长为1,P是AD的中点,求二面角的大小。3.垂面法例7., (1)求证:;(2)求二面角的大小;(3)求异面直线SC与AB所成角的余弦值。
讲义编号:____________ 学生签名:
学员编号: 年 级: 课时数:2学员姓名: 辅导科目: 学科教师:
课 题
授课日期及时段
教学内容
教学内容
数列概念1.数列的定义:按照一定顺序排列的一列数称为数列,数列中的每个数称为该数列的项.2.通项公式:如果数列的第项与序号之间可以用一个式子表示,那么这个公式叫做这个数列的通项公式,即. 3.递推公式:如果已知数列的第一项(或前几项),且任何一项与它的前一项(或前几项)间的关系可以用一个式子来表示,即或,那么这个式子叫做数列的递推公式. 如数列中,,其中是数列的递推公式.4.数列的前项和与通项的公式①; ②.5. 数列的表示方法:解析法、图像法、列举法、递推法.6. 数列的分类:有穷数列,无穷数列;递增数列,递减数列,摆动数列,常数数列;有界数列,无界数列.①递增数列:对于任何,均有.②递减数列:对于任何,均有.③摆动数列:例如: ④常数数列:例如:6,6,6,6,…….⑤有界数列:存在正数使.⑥无界数列:对于任何正数,总有项使得. 等差数列1.等差数列的概念如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,这个数列叫做等差数列,常数称为等差数列的公差. 2.通项公式与前项和公式⑴通项公式,为首项,为公差.⑵前项和公式或.3.等差中项如果成等差数列,那么叫做与的等差中项.即:是与的等差中项,,成等差数列.4.等差数列的判定方法⑴定义法:(,是常数)是等差数列;⑵中项法:()是等差数列.5.等差数列的常用性质⑴数列是等差数列,则数列、(是常数)都是等差数列;⑵在等差数列中,等距离取出若干项也构成一个等差数列,即为等差数列,公差为.⑶;(,是常数);(,是常数,)⑷若,则;⑸若等差数列的前项和,则是等差数列;⑹当项数为,则; 当项数为,则.等比数列1.等比数列的概念如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,这个数列叫做等比数列,常数称为等比数列的公比. 2.通项公式与前项和公式⑴通项公式:,为首项,为公比 .⑵前项和公式:①当时,②当时,.3.等比中项如果成等比数列,那么叫做与的等比中项.即:是与的等差中项,,成等差数列.4.等比数列的判定方法⑴定义法:(,是常数)是等比数列;⑵中项法:()且是等比数列.5.等比数列的常用性质⑴数列是等比数列,则数列、(是常数)都是等比数列;⑵在等比数列中,等距离取出若干项也构成一个等比数列,即为等比数列,公比为.⑶⑷若,则;⑸若等比数列的前项和,则、、、是等比数列.二、典型例题A、求值类的计算题(多关于等差等比数列)1)根据基本量求解(方程的思想)1、已知为等差数列的前项和,,求;
2、等差数列 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )中,且成等 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )比数列,求数列前20项的和.3、设是公比为正数的等比数列,若,求数列前7项的和.4、已知四个实数,前三个数成等差数列,后三个数成等比数列,首末两数之和为,中间两数之和为,求这四个数.2)根据数列的性质求解(整体思想)1、已知为等差数列的前项和,,则 ;2、设、分别是等差数列、的前项和,,则 .3、设是等差数列的前n项和,若( )4、等差数列,的前项和分别为,,若,则=( )5、已知为等差数列的前项和,,则 .6、在正项等比数列中,,则_______。7、已知数列是等差数列,若 ,且,则_________。8、已知为等比数列前项和,,,则 .9、在等差数列中,若,则的值为( )10、在等比数列中,已知,,则 . 11、已知为等差数列,,则 12、等差数列中,已知一、平面与平面的垂直关系1.判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。例1.在空间四边形ABCD中,AB=CB,AD=CD,E、F、G分别是AD、DC、CA的中点。 求证:。例2.,,E、F分别是AC、AD的中点。 求证: 。2.性质定理:若两个平面互相垂直,则在一个平面内垂直于它们交线的直线垂直于另一个平面。例3.在正方体ABCD—A1B1C1D1中,求A1B和平面A1B1CD所成的角.。二、二面角的基本求法1.定义法:在棱上取点,分别在两面内引两条射线与棱垂直。例4.在正方体ABCD—A1B1C1D1中, 求(1)二面角的大小; (2)平面与平面所成角的正切值。练习:过正方形ABCD的顶点A作,设PA=AB=,求二面角的大小。2.三垂线法例5.是正方形,ABEF是矩形且AF=AD=,G是EF的中点,(1)求证:;(2)求GB与平面AGC所成角的正弦值;(3)求二面角的大小。例6.点P在平面ABC外,是等腰直角三角形,,是正三角形,。(1)求证:;(2)求二面角的大小。练习:正方体ABCD—A1B1C1D1的棱长为1,P是AD的中点,求二面角的大小。3.垂面法例7., (1)求证:;(2)求二面角的大小;(3)求异面直线SC与AB所成角的余弦值。
