河南省洛阳市中成外国语学校人教版高二数学选修2-1课件:2-3 双曲线(共31张PPT)
文档属性
| 名称 | 河南省洛阳市中成外国语学校人教版高二数学选修2-1课件:2-3 双曲线(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 612.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-15 00:00:00 | ||
图片预览








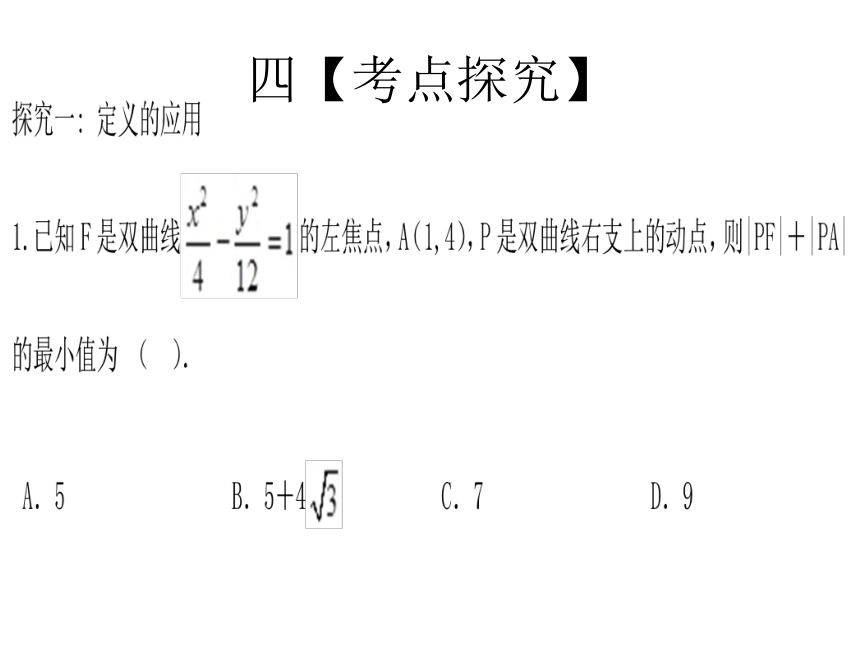



文档简介
课件31张PPT。双曲线高洪海 15年11月一【考纲要求】1.了解双曲线的实际背景,了解双曲线在刻画现实世界和解决实际问题中的作用.
2.了解双曲线的定义、几何图形和标准方程,知道它的简单几何性质(范围、对称性、顶点、离心率、渐近线).
3.了解双曲线的简单应用.
4.理解数形结合的思想.
二【知识重温】3.常用结论:三【复习自测】错误较多的有:2,5
原因:1.分不清a与2a;
2.没注意PF最小值为c-a.四【考点探究】【归纳总结】(1)双曲线定义的集合语言:P={M|||MF1|-|MF2||=2a,0<2a<|F1F2|}是解决与焦点三角形有关的计算问题的关键,切记对所求结果进行必要的检验.
(2)利用定义解决双曲线上的点与焦点的距离有关问题时,弄清点在双曲线的哪支上.
探究二: 求双曲线的标准方程【归纳总结】(1)双曲线标准方程的确定,一要考虑焦点所在的坐标轴从而确定方程形式;二要根据两个独立条件求出a2、b2.并且注意a>0,b>0,a2+b2=c2及它们的含义.
(2)在解题过程中要熟悉各元素(a,b,c,e)之间的关系,做到灵活转换,注意方程思想的使用.如果已知双曲线的渐近线:bx±ay=0,则可设双曲线方程为b2x2±a2y2=λ(λ≠0);如果双曲线过两个已知点,则可设方程为mx2+ny2=1(mn<0).
探究三: 双曲线的性质【归纳总结】1.双曲线的几何性质的实质是围绕双曲线中的“六点”(两个焦点、两个顶点、两个虚轴的端点),“四线”(两条对称轴、两条渐近线),“两形”(中心、焦点以及虚轴端点构成的三角形,双曲线上一点和两焦点构成的三角形)研究它们之间的相互联系.
2.双曲线的形状与e的关系:k=ba=c2-a2a=c2a2-1=e2-1,e越大,即渐近线的斜率的绝对值就越大,这时双曲线的形状就从扁狭逐渐变得开阔.由此可知,双曲线的离心率越大,它的开口就越阔.
3.双曲线的几何性质重要的就是渐近线和离心率,求解双曲线的离心率其关键是建立其一个关于a,b,c的方程,通过这个方程和b与a,c的关系消掉b后,建立a,c之间的方程,通过这个方程只要能求出ca即可,不一定具体求出a,c的数值.求双曲线的离心率的取值范围其关键是建立其一个关于a,b,c的不等式。
探究四: 双曲线的综合【归纳总结】直线和双曲线公共点问题,可以转化为它们的方程所组成的方程组求解的问题, 从而用代数方法判断直线与曲线的位置关系。 解题步骤是: (1)直线的斜率不存在,直线的斜率存,(2)联立直线和曲线的方程组; (3)讨论类一元二次方程(4)一元二次方程的判别式(5)韦达定理,同类坐标变换 (6)同点纵横坐标变换(7)x,y,k(斜率)的取值范围 (8)目标:弦长,中点,垂直,角度,向量,面积,范围等等五【随堂检测】
2.了解双曲线的定义、几何图形和标准方程,知道它的简单几何性质(范围、对称性、顶点、离心率、渐近线).
3.了解双曲线的简单应用.
4.理解数形结合的思想.
二【知识重温】3.常用结论:三【复习自测】错误较多的有:2,5
原因:1.分不清a与2a;
2.没注意PF最小值为c-a.四【考点探究】【归纳总结】(1)双曲线定义的集合语言:P={M|||MF1|-|MF2||=2a,0<2a<|F1F2|}是解决与焦点三角形有关的计算问题的关键,切记对所求结果进行必要的检验.
(2)利用定义解决双曲线上的点与焦点的距离有关问题时,弄清点在双曲线的哪支上.
探究二: 求双曲线的标准方程【归纳总结】(1)双曲线标准方程的确定,一要考虑焦点所在的坐标轴从而确定方程形式;二要根据两个独立条件求出a2、b2.并且注意a>0,b>0,a2+b2=c2及它们的含义.
(2)在解题过程中要熟悉各元素(a,b,c,e)之间的关系,做到灵活转换,注意方程思想的使用.如果已知双曲线的渐近线:bx±ay=0,则可设双曲线方程为b2x2±a2y2=λ(λ≠0);如果双曲线过两个已知点,则可设方程为mx2+ny2=1(mn<0).
探究三: 双曲线的性质【归纳总结】1.双曲线的几何性质的实质是围绕双曲线中的“六点”(两个焦点、两个顶点、两个虚轴的端点),“四线”(两条对称轴、两条渐近线),“两形”(中心、焦点以及虚轴端点构成的三角形,双曲线上一点和两焦点构成的三角形)研究它们之间的相互联系.
2.双曲线的形状与e的关系:k=ba=c2-a2a=c2a2-1=e2-1,e越大,即渐近线的斜率的绝对值就越大,这时双曲线的形状就从扁狭逐渐变得开阔.由此可知,双曲线的离心率越大,它的开口就越阔.
3.双曲线的几何性质重要的就是渐近线和离心率,求解双曲线的离心率其关键是建立其一个关于a,b,c的方程,通过这个方程和b与a,c的关系消掉b后,建立a,c之间的方程,通过这个方程只要能求出ca即可,不一定具体求出a,c的数值.求双曲线的离心率的取值范围其关键是建立其一个关于a,b,c的不等式。
探究四: 双曲线的综合【归纳总结】直线和双曲线公共点问题,可以转化为它们的方程所组成的方程组求解的问题, 从而用代数方法判断直线与曲线的位置关系。 解题步骤是: (1)直线的斜率不存在,直线的斜率存,(2)联立直线和曲线的方程组; (3)讨论类一元二次方程(4)一元二次方程的判别式(5)韦达定理,同类坐标变换 (6)同点纵横坐标变换(7)x,y,k(斜率)的取值范围 (8)目标:弦长,中点,垂直,角度,向量,面积,范围等等五【随堂检测】
