人教版数学七年级下册5.1.1 相交线 教案
文档属性
| 名称 | 人教版数学七年级下册5.1.1 相交线 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-11 14:57:32 | ||
图片预览

文档简介
5.1.1相交线
【教学目标】
1、知识与技能:
(1)学生能够理解相交线的定义,掌握相交线的性质。
(2)学会识别相交线所形成的角,并能正确命名。
(3)理解并掌握对顶角和邻补角的概念及性质。
2、过程与方法:
(1)通过观察、操作和归纳,让学生经历探究相交线性质的过程。
(2)培养学生的空间观念和几何直觉,提高分析问题和解决问题的能力。,
3、情感态度与价值观:
(1)激发学生对几何学习的兴趣和好奇心,培养积极探究的学习态度。
(2)让学生在探究过程中体验成功的喜悦,增强自信心和合作精神。
【教学重点】
相交线的定义和性质。
对顶角和邻补角的概念及性质。
【教学难点】
理解相交线所形成的角的种类及其命名规则。
掌握对顶角和邻补角性质的灵活运用。
【教学流程】
一、情境引入
1、观察下面的图片,你有什么发现?
这一组图片有什么共同特点?
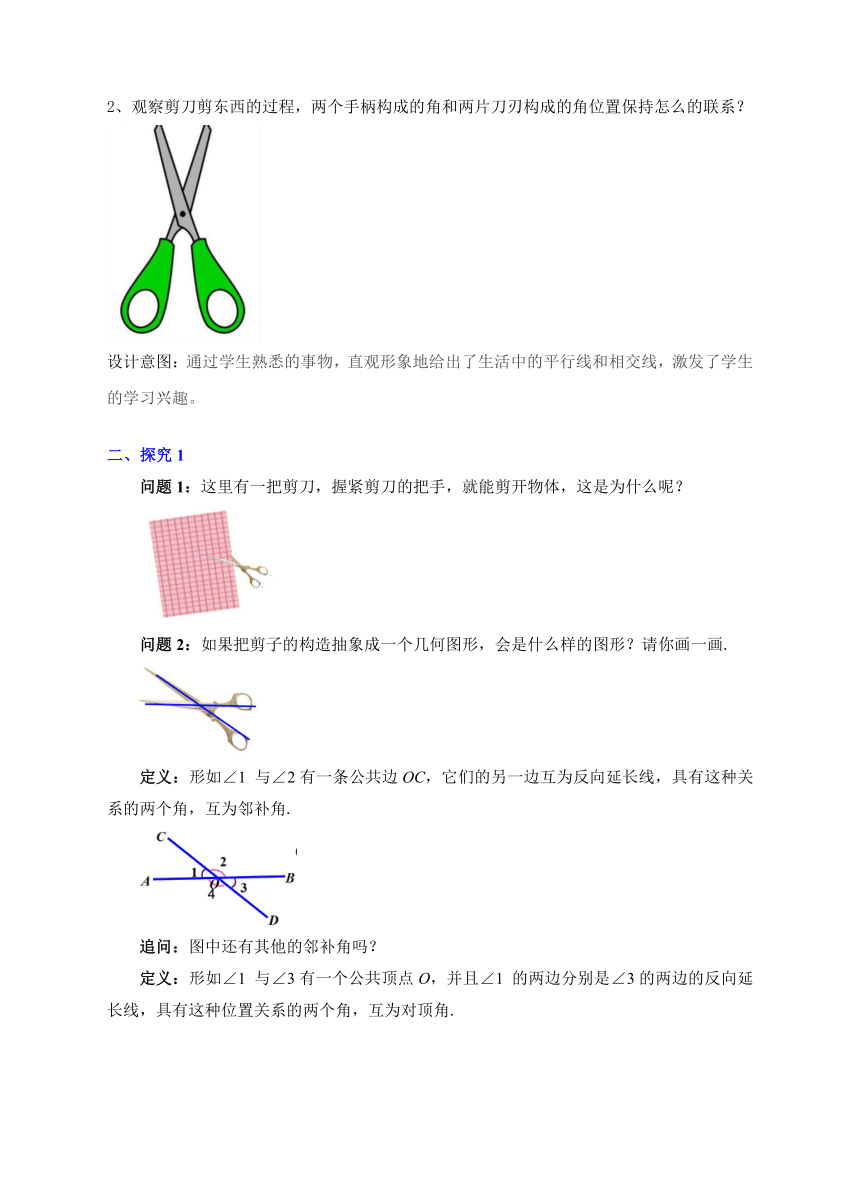
2、观察剪刀剪东西的过程,两个手柄构成的角和两片刀刃构成的角位置保持怎么的联系?
设计意图:通过学生熟悉的事物,直观形象地给出了生活中的平行线和相交线,激发了学生的学习兴趣。
二、探究1
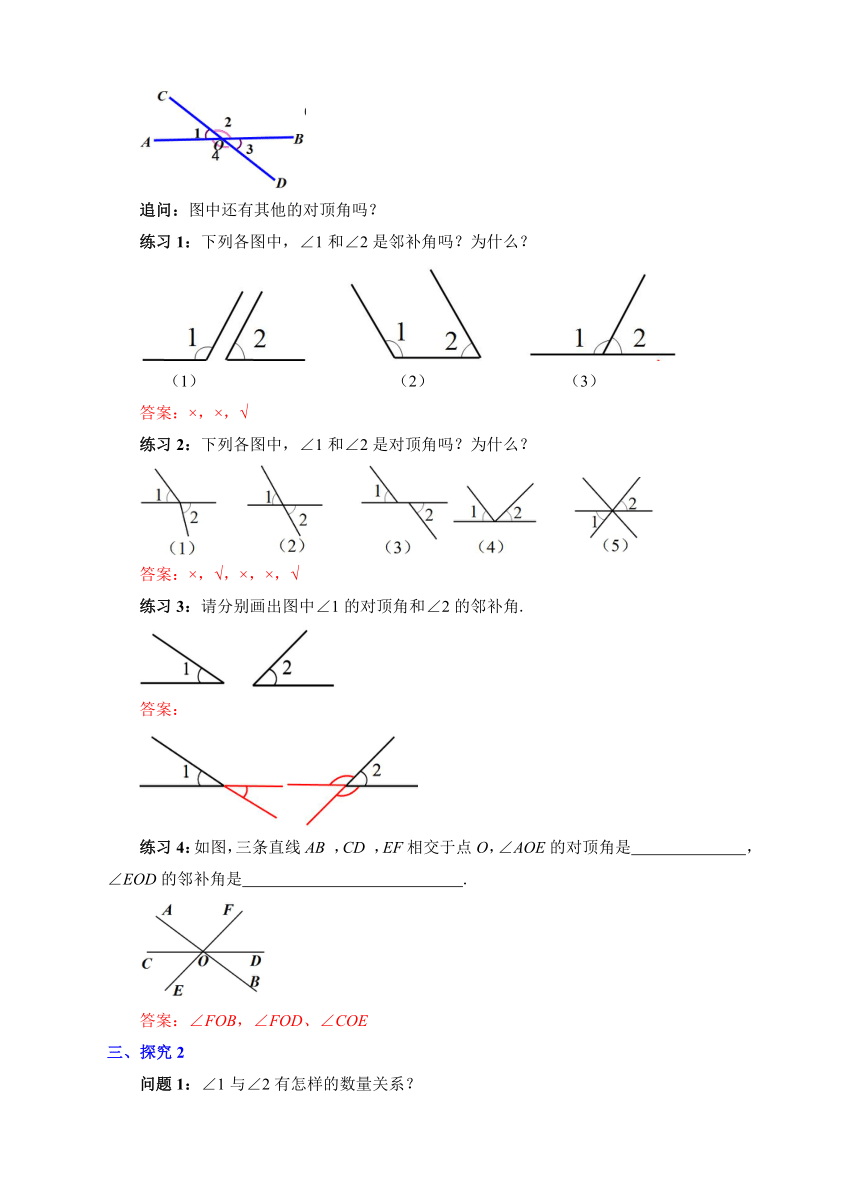
问题1:这里有一把剪刀,握紧剪刀的把手,就能剪开物体,这是为什么呢?
问题2:如果把剪子的构造抽象成一个几何图形,会是什么样的图形?请你画一画.
定义:形如∠1 与∠2有一条公共边OC,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
追问:图中还有其他的邻补角吗?
定义:形如∠1 与∠3有一个公共顶点O,并且∠1 的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
追问:图中还有其他的对顶角吗?
练习1:下列各图中,∠1和∠2是邻补角吗?为什么?
(1) (2) (3)
答案:×,×,√
练习2:下列各图中,∠1和∠2是对顶角吗?为什么?
答案:×,√,×,×,√
练习3:请分别画出图中∠1的对顶角和∠2的邻补角.
答案:
练习4:如图,三条直线AB ,CD ,EF相交于点O,∠AOE的对顶角是 , ∠EOD的邻补角是 .
答案:∠FOB,∠FOD、∠COE
三、探究2
问题1:∠1与∠2有怎样的数量关系?
性质:一对邻补角的和等于1800.
符号语言:
∵ ∠1与∠2是邻补角
∴ ∠1+∠2=1800
问题2:∠1与∠3有怎样的数量关系?
对顶角的性质:对顶角相等.
符号语言:
∵ ∠1与∠3是对顶角
∴ ∠1 =∠3
四、应用提高
例1:如图,直线a,b相交于点O,∠1=400,求∠2 ,∠3 ,∠4 的度数.
解:由邻补角定义,可得
由对顶角相等,可得
,
练习5:如图,直线a,b相交于点O,∠1+∠3=800,求∠1, ∠2 ,∠3 ,∠4 的度数.
答案:,
练习6:如图,直线a,b相交于点O,∠2是∠1的 3.5倍, 求∠1, ∠2 ,∠3 ,∠4 的度数.
答案:,
练习7:如图,直线a,b相交于点O,∠1:∠2 = 2: 7 , 求∠1, ∠2 ,∠3 ,∠4 的度数.
答案:,
五、体验收获
今天我们学习了哪些知识?
1.什么是邻补角?邻补角与补角有什么区别?
2.什么是对顶角?对顶角有什么性质?
六、达标测评
1.如图1,三条直线AB、CD、EF两两相交,在这个图形中,有对顶角_____对,邻补角____ 对.
答案:6,12
2.如图2,直线AB、CD相交于O,OE是射线.则
∠3的对顶角是_____________,
∠1的对顶角是_____________,
∠1的邻补角是_____________,
∠2的邻补角是_____________.
答案:∠AOD,∠BOD,∠3、∠AOD,∠COE
3.直线AB、CD交于点O,∠AOE= ∠DOE,∠AOC=50°求∠DOE的度数.
解: 由邻补角的定义,可得
∠AOD=180°-∠AOC
=180°-50°
=130°
因为∠AOE= ∠DOE(已知)
所以∠DOE=∠AOD÷2
=130°÷2
=65°
状元网
【教学目标】
1、知识与技能:
(1)学生能够理解相交线的定义,掌握相交线的性质。
(2)学会识别相交线所形成的角,并能正确命名。
(3)理解并掌握对顶角和邻补角的概念及性质。
2、过程与方法:
(1)通过观察、操作和归纳,让学生经历探究相交线性质的过程。
(2)培养学生的空间观念和几何直觉,提高分析问题和解决问题的能力。,
3、情感态度与价值观:
(1)激发学生对几何学习的兴趣和好奇心,培养积极探究的学习态度。
(2)让学生在探究过程中体验成功的喜悦,增强自信心和合作精神。
【教学重点】
相交线的定义和性质。
对顶角和邻补角的概念及性质。
【教学难点】
理解相交线所形成的角的种类及其命名规则。
掌握对顶角和邻补角性质的灵活运用。
【教学流程】
一、情境引入
1、观察下面的图片,你有什么发现?
这一组图片有什么共同特点?
2、观察剪刀剪东西的过程,两个手柄构成的角和两片刀刃构成的角位置保持怎么的联系?
设计意图:通过学生熟悉的事物,直观形象地给出了生活中的平行线和相交线,激发了学生的学习兴趣。
二、探究1
问题1:这里有一把剪刀,握紧剪刀的把手,就能剪开物体,这是为什么呢?
问题2:如果把剪子的构造抽象成一个几何图形,会是什么样的图形?请你画一画.
定义:形如∠1 与∠2有一条公共边OC,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
追问:图中还有其他的邻补角吗?
定义:形如∠1 与∠3有一个公共顶点O,并且∠1 的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
追问:图中还有其他的对顶角吗?
练习1:下列各图中,∠1和∠2是邻补角吗?为什么?
(1) (2) (3)
答案:×,×,√
练习2:下列各图中,∠1和∠2是对顶角吗?为什么?
答案:×,√,×,×,√
练习3:请分别画出图中∠1的对顶角和∠2的邻补角.
答案:
练习4:如图,三条直线AB ,CD ,EF相交于点O,∠AOE的对顶角是 , ∠EOD的邻补角是 .
答案:∠FOB,∠FOD、∠COE
三、探究2
问题1:∠1与∠2有怎样的数量关系?
性质:一对邻补角的和等于1800.
符号语言:
∵ ∠1与∠2是邻补角
∴ ∠1+∠2=1800
问题2:∠1与∠3有怎样的数量关系?
对顶角的性质:对顶角相等.
符号语言:
∵ ∠1与∠3是对顶角
∴ ∠1 =∠3
四、应用提高
例1:如图,直线a,b相交于点O,∠1=400,求∠2 ,∠3 ,∠4 的度数.
解:由邻补角定义,可得
由对顶角相等,可得
,
练习5:如图,直线a,b相交于点O,∠1+∠3=800,求∠1, ∠2 ,∠3 ,∠4 的度数.
答案:,
练习6:如图,直线a,b相交于点O,∠2是∠1的 3.5倍, 求∠1, ∠2 ,∠3 ,∠4 的度数.
答案:,
练习7:如图,直线a,b相交于点O,∠1:∠2 = 2: 7 , 求∠1, ∠2 ,∠3 ,∠4 的度数.
答案:,
五、体验收获
今天我们学习了哪些知识?
1.什么是邻补角?邻补角与补角有什么区别?
2.什么是对顶角?对顶角有什么性质?
六、达标测评
1.如图1,三条直线AB、CD、EF两两相交,在这个图形中,有对顶角_____对,邻补角____ 对.
答案:6,12
2.如图2,直线AB、CD相交于O,OE是射线.则
∠3的对顶角是_____________,
∠1的对顶角是_____________,
∠1的邻补角是_____________,
∠2的邻补角是_____________.
答案:∠AOD,∠BOD,∠3、∠AOD,∠COE
3.直线AB、CD交于点O,∠AOE= ∠DOE,∠AOC=50°求∠DOE的度数.
解: 由邻补角的定义,可得
∠AOD=180°-∠AOC
=180°-50°
=130°
因为∠AOE= ∠DOE(已知)
所以∠DOE=∠AOD÷2
=130°÷2
=65°
状元网
