人教版数学七年级上册 第2章 整式的加减 单元设计
文档属性
| 名称 | 人教版数学七年级上册 第2章 整式的加减 单元设计 |
|
|
| 格式 | doc | ||
| 文件大小 | 250.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-11 15:17:20 | ||
图片预览




文档简介
人教版 七年级上册
第二章 整式的加减
一、教材分析:
本章是上一章有理数等知识的延伸,内容主要包括整式、单项式、多项式;合并同类项,去括号;整式的加减法.这些内容既是对有理数的概括与抽象,又是后继学习整式的乘除、分式和根式的运算、方程、不等式、函数等知识的基础,也是学习物理、化学等学科及其他科学技术不可缺少的工具.
整式的加减实际上是对整式施行两种重要的恒等变形:一种是合并同类项;另一种是去括号.整式的恒等变形是数学中符号运算的基础,是解方程的工具,后继学习的代数内容几乎都与本章有关.同时,本章也是培养和发展学生符号感的重要素材.合并同类项是整式加减的基础,整式的加减主要是通过合并同类项把整式化简,去括号是多项式的一种恒等变形,要根据去括号的法则进行,掌握法则的关键是将括号与括号前面的符号看成统一体,不能拆开,这一点学生不容易理解,要结合例题进行分析.
有理数的省略加号的和、运算律,比较集中地体现在本章的合并同类项和去括号中,对此应有足够的认识,弄清算理,也就抓住了本章的关键.本章是初中阶段要求学生重点掌握的内容之一,是中考必考内容,主要考查用字母表示数、运算能力、观察能力、解决实际问题的能力,题型以填空题、选择题为主,单独命题较少.创新性的题目,比如规律探索题,考查学生从特殊到一般的思维意识.
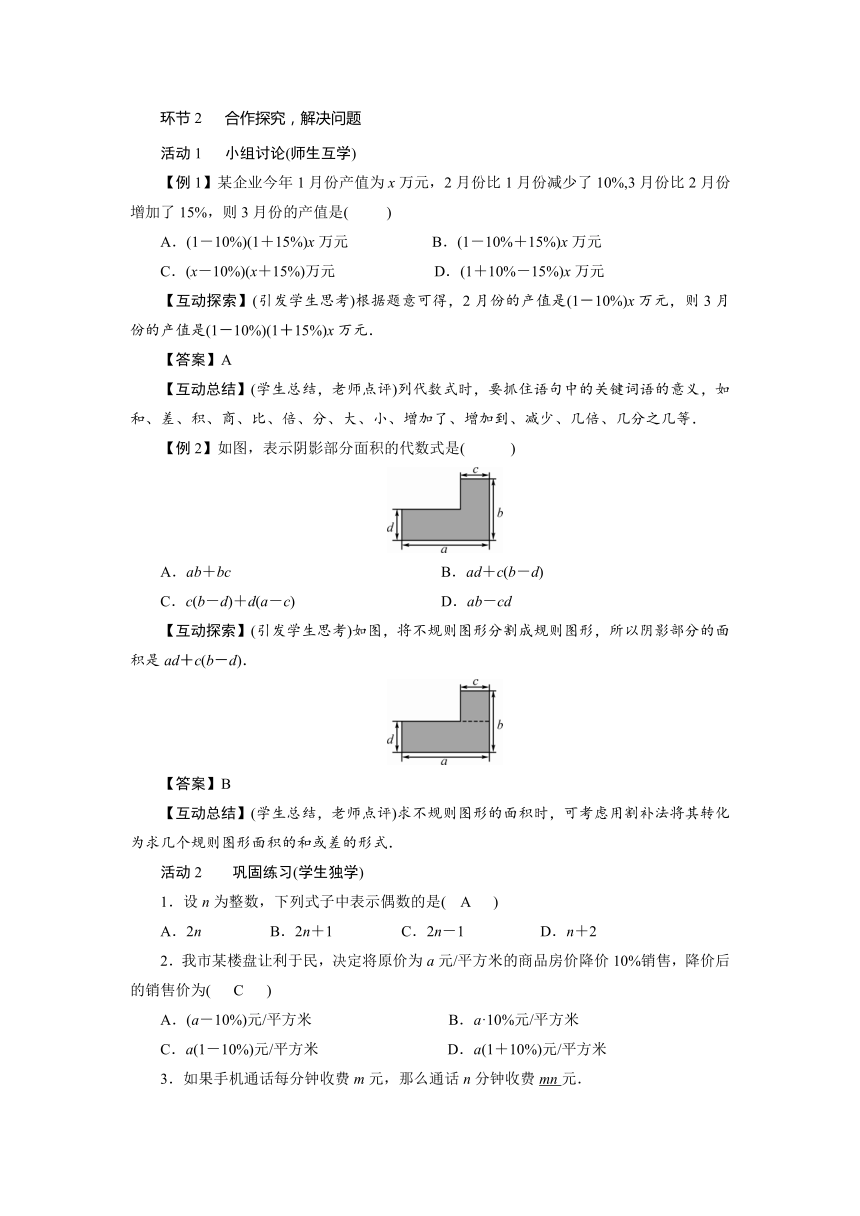
思维导图:
学情分析:
数学基础知识不扎实,主要表现在全班有四分之三的学生混合计算能力不过关,有二分之一的学生在小学时就没有好好学习,深层次的代数式无法自我探究,而全班学生的口头表达能力和实际操作都很薄弱。
四、教学目标:
1.理解同类项的概念,并能正确辨别同类项。
2.掌握合并同类项的方法。
3.掌握整式加减的方法。
4.培养学生合作交流的意识和探索精神。重点整式加减运算的一般步骤,能正确地进行整式的加减运算。难点利用整式的加减运算,解决简单的实际问题。
五、课时计划:
2.1 整式 3课时
2.2 整式的加减 3课时
六、教学过程:
2.1 整式
第1课时 用字母表示数
一、基本目标
1.使学生理解用字母表示数的意义.
2.掌握用字母表示数量关系的方法和技巧.
3.在探索现实世界数量关系的过程中,建立符号意识,初步体会数学中的抽象思维.
二、重难点目标
【教学重点】
理解用字母表示数的意义.
【教学难点】
用含有字母的式子表示实际问题中的数量关系.
三、教学过程:
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P54~P55的内容,完成下面练习.
【3 min反馈】
1.用字母表示:
(1)有理数减法法则:a-b=a+(-b);
(2)有理数除法法则:a÷b=a·(b≠0).
2.客车每小时行v千米,t小时行的路程为vt千米.
3.一本名著有a页,王红读了b天,还剩c页未读,王红平均每天读了页.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】某企业今年1月份产值为x万元,2月份比1月份减少了10%,3月份比2月份增加了15%,则3月份的产值是( )
A.(1-10%)(1+15%)x万元 B.(1-10%+15%)x万元
C.(x-10%)(x+15%)万元 D.(1+10%-15%)x万元
【互动探索】(引发学生思考)根据题意可得,2月份的产值是(1-10%)x万元,则3月份的产值是(1-10%)(1+15%)x万元.
【答案】A
【互动总结】(学生总结,老师点评)列代数式时,要抓住语句中的关键词语的意义,如和、差、积、商、比、倍、分、大、小、增加了、增加到、减少、几倍、几分之几等.
【例2】如图,表示阴影部分面积的代数式是( )
A.ab+bc B.ad+c(b-d)
C.c(b-d)+d(a-c) D.ab-cd
【互动探索】(引发学生思考)如图,将不规则图形分割成规则图形,所以阴影部分的面积是ad+c(b-d).
【答案】B
【互动总结】(学生总结,老师点评)求不规则图形的面积时,可考虑用割补法将其转化为求几个规则图形面积的和或差的形式.
活动2 巩固练习(学生独学)
1.设n为整数,下列式子中表示偶数的是( A )
A.2n B.2n+1 C.2n-1 D.n+2
2.我市某楼盘让利于民,决定将原价为a元/平方米的商品房价降价10%销售,降价后的销售价为( C )
A.(a-10%)元/平方米 B.a·10%元/平方米
C.a(1-10%)元/平方米 D.a(1+10%)元/平方米
3.如果手机通话每分钟收费m元,那么通话n分钟收费mn元.
4.用代数式表示:
(1)a与3的和的2倍;
(2)a、b的平方的和;
(3)n与1的和除以n与a的差;
(4)某厂1月份产量为a吨,以后每个月比上一个月增产x%,求该厂3月份的产量.
解:(1)2(a+3). (2)a2+b2. (3). (4)a(1+x%)2吨.
活动3 拓展延伸(学生对学)
【例3】如图是用长度相等的小棒按一定规律摆成的一组图案,第1个图案中有6根小棒,第2个图案中有11根小棒,…,则第n个图案中有________根小棒.
【互动探索】由图可知,第1个图案中有5+1=6(根)小棒;第2个图案中有2×5+1=11(根)小棒;第3个图案中有3×5+1=16(根)小棒;…;由此得出第n个图案中有5n+1根小棒.
【答案】5n+1
【互动总结】(学生总结,老师点评)要先观察图形,找出图形之间的联系,得出规律,利用规律解决问题.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
用字母表示数
四、练习设计:
请完成本课时对应练习!
第2课时 单项式
一、基本目标
1.使学生理解单项式及单项式的系数、次数的概念,并能找出单项式的系数、次数.
2.初步学会观察、对比、归纳的方法;发展学生的观察能力、思维能力及分析能力.
二、重难点目标
【教学重点】
掌握单项式及单项式的系数、次数的概念.
【教学难点】
能正确识别单项式的系数、次数.
三、教学过程:
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P56~P57的内容,完成下面练习.
【3 min反馈】
1.由数与字母或字母与字母相乘组成的代数式叫做单项式.
2.单项式中的数字因数叫做这个单项式的系数.
3.单项式中所有字母的指数的和叫做单项式的次数.
4.在式子1,a2,a-b,y,x,中,是单项式的有1,a2,y,x.
5.(1)-a的系数是-1,次数是1;
(2)单项式-3x2的系数是-3,次数是2;
(3)的系数是,次数是5.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】用单项式填空,并指出它们的系数和次数.
(1)每包书有12册,n包书有________册;
(2)底边长为a cm,高为h cm的三角形的面积是________ cm2;
(3)棱长为a cm的正方体的体积是________ cm3;
(4)一台电视机原价b元,现按原价的9折出售,这台电视机现在的售价是________元;
(5)一个长方形的长是0.9 m,宽是b m,这个长方形的面积是________m2.
【解答】见教材第57页例3.
【教师点拨】用字母表示数后,同一个式子可以表示不同的含义.
【例2】的系数与次数分别为( )
A.,7 B.,6 C.4π,6 D.,4
【互动探索】(引发学生思考)单项式中系数是什么?怎样求单项式的次数呢?
的系数为,次数为6.
【答案】B
【互动总结】(学生总结,老师点评)注意π是一个常数,不是字母.
活动2 巩固练习(学生独学)
1.下列各式中,次数为3的单项式是( B )
A.x3+y3 B.x2y C.x3y D.3xy
2.下列代数式中,属于单项式的是( D )
A.a+1 B.a2-b C. D.
3.填表:
单项式 2a2 -1.2h 3xy2 -2t2 -0.3vt
系数
次数
解:如下表:
单项式 2a2 -1.2h 3xy2 -2t2 -0.3vt
系数 2 -1.2 3 -2 -0.3
次数 2 1 3 2 2
4.若关于x、y的单项式2xym与-ax2y2的系数、次数相同,试求a、m的值.
解:因为关于x、y的单项式2xym与-ax2y2系数、次数相同,
所以-a=2,1+m=4,
解得a=-2,m=3.
活动3 拓展延伸(学生对学)
【例3】观察下列各式:
-a,a2,-a3,a4,-a5,a6,…
(1)写出第2017个和2018个单项式;
(2)写出第n个单项式.
【互动探索】由-a,a2,-a3,a4,-a5,a6,…可得第n项的表达式为(-1)n.将2017和2018分别代入表达式即可得解.
【解答】(1)第2017个单项式为-,第2018个单项式为.
(2)第n个单项式为(-1)n.
【互动总结】(学生总结,老师点评)本题主要考查了单项式,解题的关键是求出单项式的排列规律.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
单项式
四、练习设计:
请完成本课时对应练习!
第3课时 多项式
一、基本目标
1.掌握多项式、整式的概念.
2.能熟练说出多项式的项数和次数.
3.通过观察、讨论、自主探究等形式,发展学生的抽象概括能力.
二、重难点目标
【教学重点】
多项式的概念及多项式的项数、次数的概念.
【教学难点】
多项式的次数.
三、教学过程:
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P57~P58的内容,完成下面练习.
【3 min反馈】
1.几个单项式的和叫做多项式,每个单项式叫做多项式的项,次数最高项的次数叫做多项式的次数,不含字母的项叫做多项式的常数项.
2.单项式和多项式统称为整式.
3.多项式3a3-中,常数项是( D )
A.1 B.-1 C. D.-
4.多项式3x2y-4xy-1由单项式3x2y,-4xy,-1组成,它是三次三项式,其中二次项是-4xy,常数项是-1.
5.多项式-m2n2+m3-2n-3是四次四项式,最高次项的系数为-1,常数项是-3.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】指出下列多项式的项和次数:
(1)a3-a2b+ab2-b3; (2)3n4-2n2+1.
【互动探索】(引发学生思考)什么是多项式的项?什么是多项式的次数?
【解答】(1)多项式的项:a3,-a2b,ab2,-b3,多项式的次数是3.
(2)多项式的项:3n4,-2n2,1,多项式的次数是4.
【互动总结】(学生总结,老师点评)此题考查的是多项式的定义,多项式中每个单项式叫做多项式的项.多项式里,次数最高项的次数,叫做多项式的次数.
【例2】下列代数式中,哪些是整式?哪些是单项式?哪些是多项式?
,,,2x+y,-2xy2,,ab,π,-2x+y2,.
【互动探索】(引发学生思考)多项式与单项式的区别在哪里?单项式都属于整式吗?多项式呢?
【解答】整式有:,2x+y,-2xy2,ab,π,-2x+y2,.
单项式有:,-2xy2,ab,π.
多项式有:2x+y,-2x+y2,.
【互动总结】(学生总结,老师点评)既不是单项式,也不是多项式的代数式,一定不是整式.
活动2 巩固练习(学生独学)
1.已知多项式4x3-3x2+x-5,下列说法错误的是( B )
A.三次项的系数是4 B.二次项的系数是3
C.一次项的系数是1 D.常数项是-5
2.下列说法中正确的有( A )
①单项式-πx2y的系数是-;
②多项式a+3b+ab是一次多项式;
③多项式3a2b3-4ab+2的第二项是4ab;
④2x2+-3是多项式.
A.0个 B.1个 C.2个 D.3个
3.下列各式中是整式的是①②③④⑤⑥⑦⑧,是多项式的是③⑥,是单项式的是①②④⑤⑦⑧.(填序号)
①0;②x2;③-x2-2x+5;④;⑤xy;⑥8+;⑦-5;⑧.
4.指出下列多项式的项和次数.
(1)x3-x+1;
(2)3x3-2x2y2+3y2.
解:(1)多项式的项:x3,-x,1,多项式的次数是3.
(2)多项式的项:3x3,-2x2y2,3y2,多项式的次数是4.
活动3 拓展延伸(学生对学)
【例3】已知多项式xm+1y2+2xy2-4x3+1是六次四项式,单项式26x2ny5-m的次数与该多项式的次数相同,求(-m)3+2n的值.
【互动探索】利用多项式与单项式的次数与系数的确定方法得出关于m与n的方程进而得出答案.
【解答】因为多项式是六次四项式,
所以m+1+2=6,解得m=3.
故单项式26x2ny5-m=26x2ny2,
所以2n+2=6,解得n=2.
故(-m)3+2n=(-3)3+2×2=-23.
【互动总结】(学生总结,老师点评)利用多项式、单项式的次数的定义,正确得出待定的字母的取值后,代入代数式求值即可.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
整式
四、练习设计:
请完成本课时对应练习!
2.2 整式的加减
第1课时 合并同类项
一、基本目标
1.理解同类项的概念,在具体情境中认识同类项.
2.理解合并同类项的概念,掌握合并同类项的法则.
二、重难点目标
【教学重点】
理解同类项的概念,掌握合并同类项的法则.
【教学难点】
根据同类项的概念在多项式中找同类项,并能正确地合并.
三、教学过程:
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P62~P65的内容,完成下面练习.
【3 min反馈】
1.把多项式中的同类项合并成一项叫做合并同类项.
2.合并同类项的法则:系数相加,字母和字母指数不变.
3.判断下列各组中的两项是不是同类项,并说出原因.
(1)2a2b与2ab2; (2)3a与3b; (3)-7与; (4)-x2y3与6y3x2.
解:(1)不是,原因略. (2)不是,原因略. (3)是,原因略. (4)是,原因略.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】合并同类项:
(1)x3-2x2-x3-5+5x2+4; (2)a2-2ab+b2-2a2+2ab-4b2.
【互动探索】(引发学生思考)先找出同类项,再进行合并.
【解答】(1)原式=(x3-x3)+(5x2-2x2)+4-5
=(1-1)x3+(-2+5)x2+(4-5)
=3x2-1.
(2)原式=(a2-2a2)+(-2ab+2ab)+(b2-4b2)
=-a2-3b2.
【互动总结】(学生总结,老师点评)合并同类项时,只能把同类项合并成一项,不是同类项的不能合并;不能合并的项,在每步运算时不能漏掉.
【例2】(1)求多项式2x2-5x+x2+4x-3x2-2的值,其中x=;
(2)求多项式3a+abc-c2-3a+c2的值,其中a=-,b=2,c=-3.
【解答】见教材第64页例2.
活动2 巩固练习(学生独学)
1.下列各组式子中是同类项的有( B )
①-2xy3与3xy3;②-acb与-6xyz;③0与-;④3ab2与-6a2b;⑤-xy2与y2x;⑥-πm2n与5m2n.
A.3组 B.4组 C.5组 D.6组
2.若2x2yn与-3xmy4是同类项,则m=2,n=4.
3.合并同类项.
(1)2xy2-3xy2-6xy2; (2)2a2-3a-3a2+5a.
解:(1)原式=(2-3-6)xy2
=-7xy2.
(2)原式=(2-3)a2+(-3+5)a
=-a2+2a.
4.若a2xb3y与3a4b6是同类项,求3y3-4x3y-4y3+2x3y的值.
解:由a2xb3y与3a4b6是同类项,知2x=4,3y=6,可得x=2,y=2.
故原式=3y3-4y3-4x3y+2x3y
=-y3-2x3y
=-23-2×23×2
=-40.
活动3 拓展延伸(学生对学)
【例3】已知关于x、y多项式mx2+4xy-x-2x2+2nxy-3y合并后不含有二次项,求nm的值.
【互动探索】该多项式合并后不含二次项是指该多相式中二次项的系数为0.
【解答】由于多项式mx2+4xy-x-2x2+2nxy-3y=(m-2)x2+(4+2n)xy-x-3y合并后不含有二次项,
即二次项系数为0,
所以m-2=0,2n+4=0,
解得m=2,n=-2,
故nm=(-2)2=4.
【互动总结】(学生总结,老师点评)在多项式中不含哪一项,则哪一项的系数为0,由此建立方程,解方程即可求得待定系数的值.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
合并同类项
四、练习设计:
请完成本课时对应练习!
第2课时 去括号
一、基本目标
1.能运用运算律探究去括号法则,并且利用去括号法则将整式化简.
2.经历带有括号的有理数的运算,发现去括号时符号变化的规律,归纳出去括号法则,培养学生观察、分析、归纳能力.
二、重难点目标
【教学重点】
准确应用去括号法则将整式化简.
【教学难点】
去括号法则的理解;括号前面是负号时,去括号后各项符号的变化.
三、教学过程:
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P65~P67的内容,完成下面练习.
【3 min反馈】
1.去括号时,如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
2.去括号:
(1)-(-a+b)+(-c+d)=a-b-c+d;
(2)x-3(y-1)=x-3y+3;
(3)-2(-y+8x)=2y-16x.
3.下列去括号过程是否正确?若不正确,请改正.
(1)a-(-b+c-d)=a+b+c-d;
(2)a+(b-c-d)=a+b+c+d;
(3)-(a-b)+(c-d)=-a-b+c-d.
解:(1)不正确,改正:a-(-b+c-d)=a+b-c+d.
(2)不正确,改正:a+(b-c-d)=a+b-c-d.
(3)不正确,改正:-(a-b)+(c-d)=-a+b+c-d.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】去括号,合并同类项:
(1)-3(2x-3)+7x+8; (2)3-(4x2-3y2).
【互动探索】(引发学生思考)去括号时,括号外的因数是正数,去括号后原括号内各项的符号变化吗?负数呢?
【解答】(1)原式=-6x+9+7x+8
=(-6x+7x)+(9+8)
=x+17.
(2)原式=3x2-y2-2x2+y2
=3x2-2x2+
=x2.
【互动总结】(学生总结,老师点评)本题主要考查了去括号与添括号及合并同类项,解题的关键是熟记去括号与添括号及合并同类项的法则.
【例2】已知x+4y=-1,xy=5,求(6xy+7y)+[8x-(5xy-y+6x)]的值.
【互动探索】(引发学生思考)先化简整式,再根据化简后整式的特点利用整体代入法求值.
【解答】
原式=(6xy+7y)+[8x-5xy+y-6x]
=6xy+7y+8x-5xy+y-6x
=xy+8y+2x
=xy+2(x+4y)
=5+2×(-1)
=3.
【互动总结】(学生总结,老师点评)本题是求整式的值,注意一定要先化简,再求值.化简即先去括号,再合并同类项.对于本题应运用整体代入的思想求解.
活动2 巩固练习(学生独学)
1.当a=5时,则(a2-a)-(a2-2a+1)的值为( A )
A.4 B.-4 C.-14 D.1
2.去括号,并合并同类项:
(1)-(5m+n)-7(m-3n); (2)-2(xy-3y2)-[2y2-(5xy+x2)+2xy].
解:(1)-12m+20n. (2)xy+4y2+x2.
活动3 拓展延伸(学生对学)
【例3】有这样一道题:计算(2x3-3x2y-2xy2)-(x3-2xy2+y3)+(-x3+3x2y-y3)的值,其中x=2,y=-1.甲同学把x=2误抄成x=-2,但他计算的结果也是正确的,试说明理由,并求出这个结果.
【互动探索】将原式去括号合并同类项得到最简结果,根据题意判断即可.
【解答】原式=2x3-3x2y-2xy2-x3+2xy2-y3-x3+3x2y-y3=-2y3.
结果与x取值无关,故甲同学把x=2误抄成x=-2,但他计算的结果也是正确的.当y=-1时,原式=2.
【互动总结】(学生总结,老师点评)此题考查了整式的加减——化简求值,熟练掌握运算法则是解本题的关键.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
去括号
四、练习设计:
请完成本课时对应练习!
第3课时 整式的加减
一、基本目标
1.掌握整式的加减的运算法则,会进行整式的加减运算.
2.能运用整式的加减运算解决一些简单的问题.
二、重难点目标
【教学重点】
整式加减的运算法则.
【教学难点】
概括整式加减的运算法则并灵活、准确地运用法则.
三、教学过程:
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P67~P70的内容,完成下面练习.
【3 min反馈】
1.整式加减混合运算法则:一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
2.多项式-a2-1与3a2-2a+1的和为( A )
A.2a2-2a B.4a2-2a+2 C.4a2-2a-2 D.2a2+2a
3.计算:5ab2+2ab2-(-6ab2)=13ab2.
4.如果长方形的周长为10a+6b,宽为2a-b,那么长为3a+4b.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】先化简,再求值:-m2n+(2mn2-3m2n)-2(mn2-3m2n),其中m=-1,n=2.
【互动探索】(引发学生思考)先对整式化简,再代入求值.
【解答】原式=-m2n+2mn2-3m2n-2mn2+3m2n=-m2n.
当m=-1,n=2时,
原式=-(-1)2×2=-2.
【互动总结】(学生总结,老师点评)此题主要考查了整式的加减——化简求值问题,要熟练掌握,一般要先化简,再把给定字母的值代入计算,得出整式的值,不能把数值直接代入整式中计算.
【例2】已知A=-4x2-4xy+1,B=x2+xy-5,求2B-A的值.
【互动探索】(引发学生思考)题中2B怎样表示?计算时要注意些什么?
【解答】2B-A=2(x2+xy-5)-(-4x2-4xy+1)
=2x2+2xy-10+4x2+4xy-1
=6x2+6xy-11.
【互动总结】(学生总结,老师点评)本题考查的是整式的加减运算,掌握合并同类项法则是解题的关键.
活动2 巩固练习(学生独学)
1.化简a-(5a-3b)+(2b-a)的结果是( B )
A.7a-b B.-5a+5b C.7a+5b D.-5a-b
2.若A=x2-xy,B=2xy+2y2,则2A+B为( A )
A.2x2+2y2 B.4xy C.-4xy D.2x2-2y2
3.x2-x+5减去3x2-4的结果是-2x2-x+9.
4.(1)化简:3a3-(3a2+b2-5b)+a2-5b+b2;
(2)先化简,再求值:x-2(x-y2)+(-x+y2),其中x=2,y=-.
解:(1)原式=3a3-3a2-b2+5b+a2-5b+b2
=3a3-2a2.
(2)原式=x-2x+2y2-x+y2
=-2x+3y2.
当x=2,y=-时,
原式=-2×2+3×2
=-4+
=-
活动3 拓展延伸(学生对学)
【例3】某天数学课上老师讲了整式的加减运算,小颖回家后拿出自己的课堂笔记,复习老师在课堂上所讲的内容,她突然发现一道题目:5(2a2+3ab-b2)-(-3+ab+5a2+b2)=5a2-6b2+3被墨水弄脏了,则被墨水弄脏的一项是( )
A.+14ab B.+3ab
C.+16ab D.+2ab
【互动探索】此题涉及整式加减运算,解答时只要把求出5(2a2+3ab-b2)-(-3+ab+5a2+b2)的值,再减去5a2-6b2+3即可知道被墨水弄脏的一项.
设被墨水弄脏的这一项为M,则M=5(2a2+3ab-b2)-(-3+ab+5a2+b2)-(5a2-6b2+3)=14ab.
【答案】A
【互动总结】(学生总结,老师点评)解决此类题目的关键是熟练运用去括号、合并同类项,括号前是负数,括号里的各项要变号.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
整式的加减
四、练习设计:
请完成本课时对应练习!
第二章 整式的加减
一、教材分析:
本章是上一章有理数等知识的延伸,内容主要包括整式、单项式、多项式;合并同类项,去括号;整式的加减法.这些内容既是对有理数的概括与抽象,又是后继学习整式的乘除、分式和根式的运算、方程、不等式、函数等知识的基础,也是学习物理、化学等学科及其他科学技术不可缺少的工具.
整式的加减实际上是对整式施行两种重要的恒等变形:一种是合并同类项;另一种是去括号.整式的恒等变形是数学中符号运算的基础,是解方程的工具,后继学习的代数内容几乎都与本章有关.同时,本章也是培养和发展学生符号感的重要素材.合并同类项是整式加减的基础,整式的加减主要是通过合并同类项把整式化简,去括号是多项式的一种恒等变形,要根据去括号的法则进行,掌握法则的关键是将括号与括号前面的符号看成统一体,不能拆开,这一点学生不容易理解,要结合例题进行分析.
有理数的省略加号的和、运算律,比较集中地体现在本章的合并同类项和去括号中,对此应有足够的认识,弄清算理,也就抓住了本章的关键.本章是初中阶段要求学生重点掌握的内容之一,是中考必考内容,主要考查用字母表示数、运算能力、观察能力、解决实际问题的能力,题型以填空题、选择题为主,单独命题较少.创新性的题目,比如规律探索题,考查学生从特殊到一般的思维意识.
思维导图:
学情分析:
数学基础知识不扎实,主要表现在全班有四分之三的学生混合计算能力不过关,有二分之一的学生在小学时就没有好好学习,深层次的代数式无法自我探究,而全班学生的口头表达能力和实际操作都很薄弱。
四、教学目标:
1.理解同类项的概念,并能正确辨别同类项。
2.掌握合并同类项的方法。
3.掌握整式加减的方法。
4.培养学生合作交流的意识和探索精神。重点整式加减运算的一般步骤,能正确地进行整式的加减运算。难点利用整式的加减运算,解决简单的实际问题。
五、课时计划:
2.1 整式 3课时
2.2 整式的加减 3课时
六、教学过程:
2.1 整式
第1课时 用字母表示数
一、基本目标
1.使学生理解用字母表示数的意义.
2.掌握用字母表示数量关系的方法和技巧.
3.在探索现实世界数量关系的过程中,建立符号意识,初步体会数学中的抽象思维.
二、重难点目标
【教学重点】
理解用字母表示数的意义.
【教学难点】
用含有字母的式子表示实际问题中的数量关系.
三、教学过程:
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P54~P55的内容,完成下面练习.
【3 min反馈】
1.用字母表示:
(1)有理数减法法则:a-b=a+(-b);
(2)有理数除法法则:a÷b=a·(b≠0).
2.客车每小时行v千米,t小时行的路程为vt千米.
3.一本名著有a页,王红读了b天,还剩c页未读,王红平均每天读了页.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】某企业今年1月份产值为x万元,2月份比1月份减少了10%,3月份比2月份增加了15%,则3月份的产值是( )
A.(1-10%)(1+15%)x万元 B.(1-10%+15%)x万元
C.(x-10%)(x+15%)万元 D.(1+10%-15%)x万元
【互动探索】(引发学生思考)根据题意可得,2月份的产值是(1-10%)x万元,则3月份的产值是(1-10%)(1+15%)x万元.
【答案】A
【互动总结】(学生总结,老师点评)列代数式时,要抓住语句中的关键词语的意义,如和、差、积、商、比、倍、分、大、小、增加了、增加到、减少、几倍、几分之几等.
【例2】如图,表示阴影部分面积的代数式是( )
A.ab+bc B.ad+c(b-d)
C.c(b-d)+d(a-c) D.ab-cd
【互动探索】(引发学生思考)如图,将不规则图形分割成规则图形,所以阴影部分的面积是ad+c(b-d).
【答案】B
【互动总结】(学生总结,老师点评)求不规则图形的面积时,可考虑用割补法将其转化为求几个规则图形面积的和或差的形式.
活动2 巩固练习(学生独学)
1.设n为整数,下列式子中表示偶数的是( A )
A.2n B.2n+1 C.2n-1 D.n+2
2.我市某楼盘让利于民,决定将原价为a元/平方米的商品房价降价10%销售,降价后的销售价为( C )
A.(a-10%)元/平方米 B.a·10%元/平方米
C.a(1-10%)元/平方米 D.a(1+10%)元/平方米
3.如果手机通话每分钟收费m元,那么通话n分钟收费mn元.
4.用代数式表示:
(1)a与3的和的2倍;
(2)a、b的平方的和;
(3)n与1的和除以n与a的差;
(4)某厂1月份产量为a吨,以后每个月比上一个月增产x%,求该厂3月份的产量.
解:(1)2(a+3). (2)a2+b2. (3). (4)a(1+x%)2吨.
活动3 拓展延伸(学生对学)
【例3】如图是用长度相等的小棒按一定规律摆成的一组图案,第1个图案中有6根小棒,第2个图案中有11根小棒,…,则第n个图案中有________根小棒.
【互动探索】由图可知,第1个图案中有5+1=6(根)小棒;第2个图案中有2×5+1=11(根)小棒;第3个图案中有3×5+1=16(根)小棒;…;由此得出第n个图案中有5n+1根小棒.
【答案】5n+1
【互动总结】(学生总结,老师点评)要先观察图形,找出图形之间的联系,得出规律,利用规律解决问题.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
用字母表示数
四、练习设计:
请完成本课时对应练习!
第2课时 单项式
一、基本目标
1.使学生理解单项式及单项式的系数、次数的概念,并能找出单项式的系数、次数.
2.初步学会观察、对比、归纳的方法;发展学生的观察能力、思维能力及分析能力.
二、重难点目标
【教学重点】
掌握单项式及单项式的系数、次数的概念.
【教学难点】
能正确识别单项式的系数、次数.
三、教学过程:
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P56~P57的内容,完成下面练习.
【3 min反馈】
1.由数与字母或字母与字母相乘组成的代数式叫做单项式.
2.单项式中的数字因数叫做这个单项式的系数.
3.单项式中所有字母的指数的和叫做单项式的次数.
4.在式子1,a2,a-b,y,x,中,是单项式的有1,a2,y,x.
5.(1)-a的系数是-1,次数是1;
(2)单项式-3x2的系数是-3,次数是2;
(3)的系数是,次数是5.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】用单项式填空,并指出它们的系数和次数.
(1)每包书有12册,n包书有________册;
(2)底边长为a cm,高为h cm的三角形的面积是________ cm2;
(3)棱长为a cm的正方体的体积是________ cm3;
(4)一台电视机原价b元,现按原价的9折出售,这台电视机现在的售价是________元;
(5)一个长方形的长是0.9 m,宽是b m,这个长方形的面积是________m2.
【解答】见教材第57页例3.
【教师点拨】用字母表示数后,同一个式子可以表示不同的含义.
【例2】的系数与次数分别为( )
A.,7 B.,6 C.4π,6 D.,4
【互动探索】(引发学生思考)单项式中系数是什么?怎样求单项式的次数呢?
的系数为,次数为6.
【答案】B
【互动总结】(学生总结,老师点评)注意π是一个常数,不是字母.
活动2 巩固练习(学生独学)
1.下列各式中,次数为3的单项式是( B )
A.x3+y3 B.x2y C.x3y D.3xy
2.下列代数式中,属于单项式的是( D )
A.a+1 B.a2-b C. D.
3.填表:
单项式 2a2 -1.2h 3xy2 -2t2 -0.3vt
系数
次数
解:如下表:
单项式 2a2 -1.2h 3xy2 -2t2 -0.3vt
系数 2 -1.2 3 -2 -0.3
次数 2 1 3 2 2
4.若关于x、y的单项式2xym与-ax2y2的系数、次数相同,试求a、m的值.
解:因为关于x、y的单项式2xym与-ax2y2系数、次数相同,
所以-a=2,1+m=4,
解得a=-2,m=3.
活动3 拓展延伸(学生对学)
【例3】观察下列各式:
-a,a2,-a3,a4,-a5,a6,…
(1)写出第2017个和2018个单项式;
(2)写出第n个单项式.
【互动探索】由-a,a2,-a3,a4,-a5,a6,…可得第n项的表达式为(-1)n.将2017和2018分别代入表达式即可得解.
【解答】(1)第2017个单项式为-,第2018个单项式为.
(2)第n个单项式为(-1)n.
【互动总结】(学生总结,老师点评)本题主要考查了单项式,解题的关键是求出单项式的排列规律.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
单项式
四、练习设计:
请完成本课时对应练习!
第3课时 多项式
一、基本目标
1.掌握多项式、整式的概念.
2.能熟练说出多项式的项数和次数.
3.通过观察、讨论、自主探究等形式,发展学生的抽象概括能力.
二、重难点目标
【教学重点】
多项式的概念及多项式的项数、次数的概念.
【教学难点】
多项式的次数.
三、教学过程:
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P57~P58的内容,完成下面练习.
【3 min反馈】
1.几个单项式的和叫做多项式,每个单项式叫做多项式的项,次数最高项的次数叫做多项式的次数,不含字母的项叫做多项式的常数项.
2.单项式和多项式统称为整式.
3.多项式3a3-中,常数项是( D )
A.1 B.-1 C. D.-
4.多项式3x2y-4xy-1由单项式3x2y,-4xy,-1组成,它是三次三项式,其中二次项是-4xy,常数项是-1.
5.多项式-m2n2+m3-2n-3是四次四项式,最高次项的系数为-1,常数项是-3.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】指出下列多项式的项和次数:
(1)a3-a2b+ab2-b3; (2)3n4-2n2+1.
【互动探索】(引发学生思考)什么是多项式的项?什么是多项式的次数?
【解答】(1)多项式的项:a3,-a2b,ab2,-b3,多项式的次数是3.
(2)多项式的项:3n4,-2n2,1,多项式的次数是4.
【互动总结】(学生总结,老师点评)此题考查的是多项式的定义,多项式中每个单项式叫做多项式的项.多项式里,次数最高项的次数,叫做多项式的次数.
【例2】下列代数式中,哪些是整式?哪些是单项式?哪些是多项式?
,,,2x+y,-2xy2,,ab,π,-2x+y2,.
【互动探索】(引发学生思考)多项式与单项式的区别在哪里?单项式都属于整式吗?多项式呢?
【解答】整式有:,2x+y,-2xy2,ab,π,-2x+y2,.
单项式有:,-2xy2,ab,π.
多项式有:2x+y,-2x+y2,.
【互动总结】(学生总结,老师点评)既不是单项式,也不是多项式的代数式,一定不是整式.
活动2 巩固练习(学生独学)
1.已知多项式4x3-3x2+x-5,下列说法错误的是( B )
A.三次项的系数是4 B.二次项的系数是3
C.一次项的系数是1 D.常数项是-5
2.下列说法中正确的有( A )
①单项式-πx2y的系数是-;
②多项式a+3b+ab是一次多项式;
③多项式3a2b3-4ab+2的第二项是4ab;
④2x2+-3是多项式.
A.0个 B.1个 C.2个 D.3个
3.下列各式中是整式的是①②③④⑤⑥⑦⑧,是多项式的是③⑥,是单项式的是①②④⑤⑦⑧.(填序号)
①0;②x2;③-x2-2x+5;④;⑤xy;⑥8+;⑦-5;⑧.
4.指出下列多项式的项和次数.
(1)x3-x+1;
(2)3x3-2x2y2+3y2.
解:(1)多项式的项:x3,-x,1,多项式的次数是3.
(2)多项式的项:3x3,-2x2y2,3y2,多项式的次数是4.
活动3 拓展延伸(学生对学)
【例3】已知多项式xm+1y2+2xy2-4x3+1是六次四项式,单项式26x2ny5-m的次数与该多项式的次数相同,求(-m)3+2n的值.
【互动探索】利用多项式与单项式的次数与系数的确定方法得出关于m与n的方程进而得出答案.
【解答】因为多项式是六次四项式,
所以m+1+2=6,解得m=3.
故单项式26x2ny5-m=26x2ny2,
所以2n+2=6,解得n=2.
故(-m)3+2n=(-3)3+2×2=-23.
【互动总结】(学生总结,老师点评)利用多项式、单项式的次数的定义,正确得出待定的字母的取值后,代入代数式求值即可.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
整式
四、练习设计:
请完成本课时对应练习!
2.2 整式的加减
第1课时 合并同类项
一、基本目标
1.理解同类项的概念,在具体情境中认识同类项.
2.理解合并同类项的概念,掌握合并同类项的法则.
二、重难点目标
【教学重点】
理解同类项的概念,掌握合并同类项的法则.
【教学难点】
根据同类项的概念在多项式中找同类项,并能正确地合并.
三、教学过程:
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P62~P65的内容,完成下面练习.
【3 min反馈】
1.把多项式中的同类项合并成一项叫做合并同类项.
2.合并同类项的法则:系数相加,字母和字母指数不变.
3.判断下列各组中的两项是不是同类项,并说出原因.
(1)2a2b与2ab2; (2)3a与3b; (3)-7与; (4)-x2y3与6y3x2.
解:(1)不是,原因略. (2)不是,原因略. (3)是,原因略. (4)是,原因略.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】合并同类项:
(1)x3-2x2-x3-5+5x2+4; (2)a2-2ab+b2-2a2+2ab-4b2.
【互动探索】(引发学生思考)先找出同类项,再进行合并.
【解答】(1)原式=(x3-x3)+(5x2-2x2)+4-5
=(1-1)x3+(-2+5)x2+(4-5)
=3x2-1.
(2)原式=(a2-2a2)+(-2ab+2ab)+(b2-4b2)
=-a2-3b2.
【互动总结】(学生总结,老师点评)合并同类项时,只能把同类项合并成一项,不是同类项的不能合并;不能合并的项,在每步运算时不能漏掉.
【例2】(1)求多项式2x2-5x+x2+4x-3x2-2的值,其中x=;
(2)求多项式3a+abc-c2-3a+c2的值,其中a=-,b=2,c=-3.
【解答】见教材第64页例2.
活动2 巩固练习(学生独学)
1.下列各组式子中是同类项的有( B )
①-2xy3与3xy3;②-acb与-6xyz;③0与-;④3ab2与-6a2b;⑤-xy2与y2x;⑥-πm2n与5m2n.
A.3组 B.4组 C.5组 D.6组
2.若2x2yn与-3xmy4是同类项,则m=2,n=4.
3.合并同类项.
(1)2xy2-3xy2-6xy2; (2)2a2-3a-3a2+5a.
解:(1)原式=(2-3-6)xy2
=-7xy2.
(2)原式=(2-3)a2+(-3+5)a
=-a2+2a.
4.若a2xb3y与3a4b6是同类项,求3y3-4x3y-4y3+2x3y的值.
解:由a2xb3y与3a4b6是同类项,知2x=4,3y=6,可得x=2,y=2.
故原式=3y3-4y3-4x3y+2x3y
=-y3-2x3y
=-23-2×23×2
=-40.
活动3 拓展延伸(学生对学)
【例3】已知关于x、y多项式mx2+4xy-x-2x2+2nxy-3y合并后不含有二次项,求nm的值.
【互动探索】该多项式合并后不含二次项是指该多相式中二次项的系数为0.
【解答】由于多项式mx2+4xy-x-2x2+2nxy-3y=(m-2)x2+(4+2n)xy-x-3y合并后不含有二次项,
即二次项系数为0,
所以m-2=0,2n+4=0,
解得m=2,n=-2,
故nm=(-2)2=4.
【互动总结】(学生总结,老师点评)在多项式中不含哪一项,则哪一项的系数为0,由此建立方程,解方程即可求得待定系数的值.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
合并同类项
四、练习设计:
请完成本课时对应练习!
第2课时 去括号
一、基本目标
1.能运用运算律探究去括号法则,并且利用去括号法则将整式化简.
2.经历带有括号的有理数的运算,发现去括号时符号变化的规律,归纳出去括号法则,培养学生观察、分析、归纳能力.
二、重难点目标
【教学重点】
准确应用去括号法则将整式化简.
【教学难点】
去括号法则的理解;括号前面是负号时,去括号后各项符号的变化.
三、教学过程:
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P65~P67的内容,完成下面练习.
【3 min反馈】
1.去括号时,如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
2.去括号:
(1)-(-a+b)+(-c+d)=a-b-c+d;
(2)x-3(y-1)=x-3y+3;
(3)-2(-y+8x)=2y-16x.
3.下列去括号过程是否正确?若不正确,请改正.
(1)a-(-b+c-d)=a+b+c-d;
(2)a+(b-c-d)=a+b+c+d;
(3)-(a-b)+(c-d)=-a-b+c-d.
解:(1)不正确,改正:a-(-b+c-d)=a+b-c+d.
(2)不正确,改正:a+(b-c-d)=a+b-c-d.
(3)不正确,改正:-(a-b)+(c-d)=-a+b+c-d.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】去括号,合并同类项:
(1)-3(2x-3)+7x+8; (2)3-(4x2-3y2).
【互动探索】(引发学生思考)去括号时,括号外的因数是正数,去括号后原括号内各项的符号变化吗?负数呢?
【解答】(1)原式=-6x+9+7x+8
=(-6x+7x)+(9+8)
=x+17.
(2)原式=3x2-y2-2x2+y2
=3x2-2x2+
=x2.
【互动总结】(学生总结,老师点评)本题主要考查了去括号与添括号及合并同类项,解题的关键是熟记去括号与添括号及合并同类项的法则.
【例2】已知x+4y=-1,xy=5,求(6xy+7y)+[8x-(5xy-y+6x)]的值.
【互动探索】(引发学生思考)先化简整式,再根据化简后整式的特点利用整体代入法求值.
【解答】
原式=(6xy+7y)+[8x-5xy+y-6x]
=6xy+7y+8x-5xy+y-6x
=xy+8y+2x
=xy+2(x+4y)
=5+2×(-1)
=3.
【互动总结】(学生总结,老师点评)本题是求整式的值,注意一定要先化简,再求值.化简即先去括号,再合并同类项.对于本题应运用整体代入的思想求解.
活动2 巩固练习(学生独学)
1.当a=5时,则(a2-a)-(a2-2a+1)的值为( A )
A.4 B.-4 C.-14 D.1
2.去括号,并合并同类项:
(1)-(5m+n)-7(m-3n); (2)-2(xy-3y2)-[2y2-(5xy+x2)+2xy].
解:(1)-12m+20n. (2)xy+4y2+x2.
活动3 拓展延伸(学生对学)
【例3】有这样一道题:计算(2x3-3x2y-2xy2)-(x3-2xy2+y3)+(-x3+3x2y-y3)的值,其中x=2,y=-1.甲同学把x=2误抄成x=-2,但他计算的结果也是正确的,试说明理由,并求出这个结果.
【互动探索】将原式去括号合并同类项得到最简结果,根据题意判断即可.
【解答】原式=2x3-3x2y-2xy2-x3+2xy2-y3-x3+3x2y-y3=-2y3.
结果与x取值无关,故甲同学把x=2误抄成x=-2,但他计算的结果也是正确的.当y=-1时,原式=2.
【互动总结】(学生总结,老师点评)此题考查了整式的加减——化简求值,熟练掌握运算法则是解本题的关键.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
去括号
四、练习设计:
请完成本课时对应练习!
第3课时 整式的加减
一、基本目标
1.掌握整式的加减的运算法则,会进行整式的加减运算.
2.能运用整式的加减运算解决一些简单的问题.
二、重难点目标
【教学重点】
整式加减的运算法则.
【教学难点】
概括整式加减的运算法则并灵活、准确地运用法则.
三、教学过程:
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P67~P70的内容,完成下面练习.
【3 min反馈】
1.整式加减混合运算法则:一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
2.多项式-a2-1与3a2-2a+1的和为( A )
A.2a2-2a B.4a2-2a+2 C.4a2-2a-2 D.2a2+2a
3.计算:5ab2+2ab2-(-6ab2)=13ab2.
4.如果长方形的周长为10a+6b,宽为2a-b,那么长为3a+4b.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】先化简,再求值:-m2n+(2mn2-3m2n)-2(mn2-3m2n),其中m=-1,n=2.
【互动探索】(引发学生思考)先对整式化简,再代入求值.
【解答】原式=-m2n+2mn2-3m2n-2mn2+3m2n=-m2n.
当m=-1,n=2时,
原式=-(-1)2×2=-2.
【互动总结】(学生总结,老师点评)此题主要考查了整式的加减——化简求值问题,要熟练掌握,一般要先化简,再把给定字母的值代入计算,得出整式的值,不能把数值直接代入整式中计算.
【例2】已知A=-4x2-4xy+1,B=x2+xy-5,求2B-A的值.
【互动探索】(引发学生思考)题中2B怎样表示?计算时要注意些什么?
【解答】2B-A=2(x2+xy-5)-(-4x2-4xy+1)
=2x2+2xy-10+4x2+4xy-1
=6x2+6xy-11.
【互动总结】(学生总结,老师点评)本题考查的是整式的加减运算,掌握合并同类项法则是解题的关键.
活动2 巩固练习(学生独学)
1.化简a-(5a-3b)+(2b-a)的结果是( B )
A.7a-b B.-5a+5b C.7a+5b D.-5a-b
2.若A=x2-xy,B=2xy+2y2,则2A+B为( A )
A.2x2+2y2 B.4xy C.-4xy D.2x2-2y2
3.x2-x+5减去3x2-4的结果是-2x2-x+9.
4.(1)化简:3a3-(3a2+b2-5b)+a2-5b+b2;
(2)先化简,再求值:x-2(x-y2)+(-x+y2),其中x=2,y=-.
解:(1)原式=3a3-3a2-b2+5b+a2-5b+b2
=3a3-2a2.
(2)原式=x-2x+2y2-x+y2
=-2x+3y2.
当x=2,y=-时,
原式=-2×2+3×2
=-4+
=-
活动3 拓展延伸(学生对学)
【例3】某天数学课上老师讲了整式的加减运算,小颖回家后拿出自己的课堂笔记,复习老师在课堂上所讲的内容,她突然发现一道题目:5(2a2+3ab-b2)-(-3+ab+5a2+b2)=5a2-6b2+3被墨水弄脏了,则被墨水弄脏的一项是( )
A.+14ab B.+3ab
C.+16ab D.+2ab
【互动探索】此题涉及整式加减运算,解答时只要把求出5(2a2+3ab-b2)-(-3+ab+5a2+b2)的值,再减去5a2-6b2+3即可知道被墨水弄脏的一项.
设被墨水弄脏的这一项为M,则M=5(2a2+3ab-b2)-(-3+ab+5a2+b2)-(5a2-6b2+3)=14ab.
【答案】A
【互动总结】(学生总结,老师点评)解决此类题目的关键是熟练运用去括号、合并同类项,括号前是负数,括号里的各项要变号.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
整式的加减
四、练习设计:
请完成本课时对应练习!
