【北师大版九上同步练习】 4.2 平行线分线断成比例(含答案)
文档属性
| 名称 | 【北师大版九上同步练习】 4.2 平行线分线断成比例(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 9.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-11 16:14:25 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【北师大版九上同步练习】
4.2平行线分线断成比例
一、单选题
1.如图,,直线、与这三条平行线分别交于点A、B、C和点D、E、F,,,,则的长是( )
A.8 B.9 C.11 D.12
2.如图,若,则下列各式错误的是( )
A. B. C. D.
3.如图,,点B,E分别在,上,,,的长( )
A.3 B.4 C.5 D.10
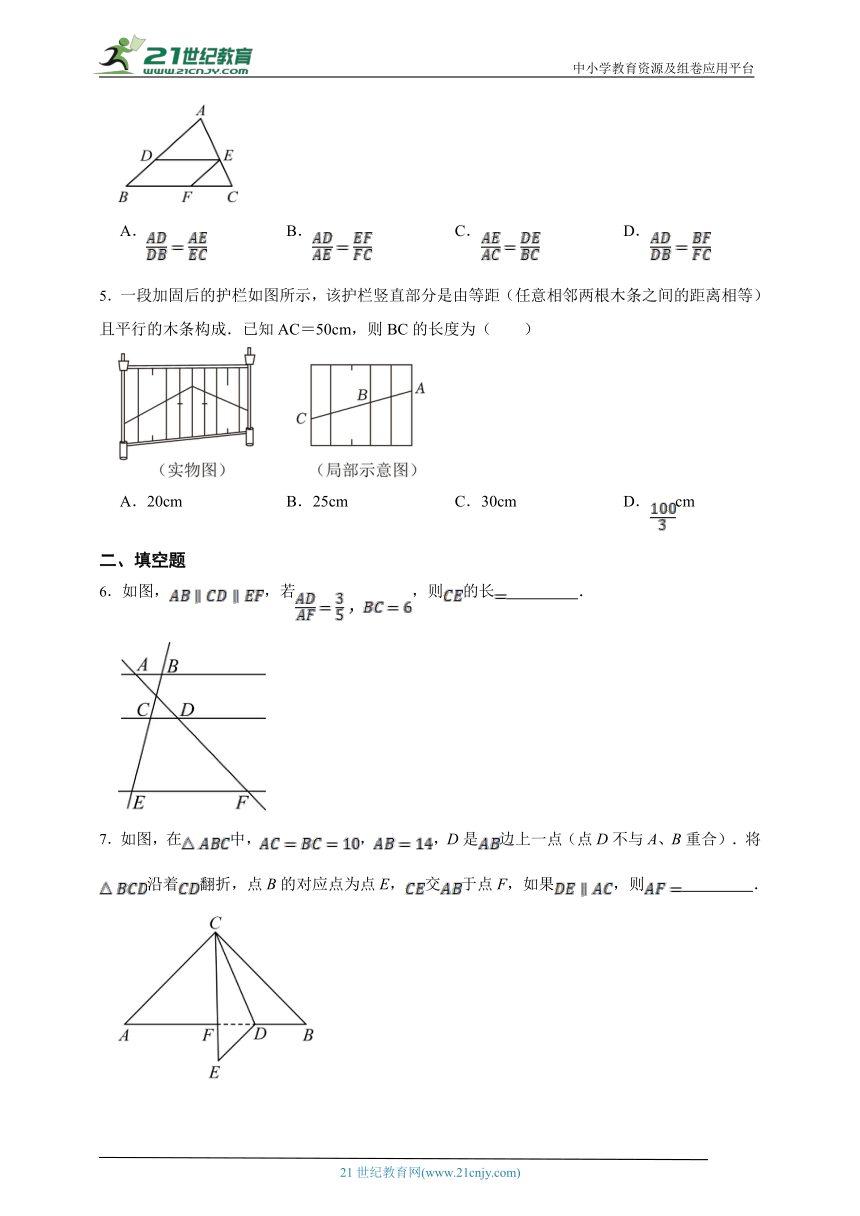
4.如图,,,则下列比例式不正确的是( )
A. B. C. D.
5.一段加固后的护栏如图所示,该护栏竖直部分是由等距(任意相邻两根木条之间的距离相等)且平行的木条构成.已知AC=50cm,则BC的长度为( )
A.20cm B.25cm C.30cm D.cm
二、填空题
6.如图,,若,则的长 .
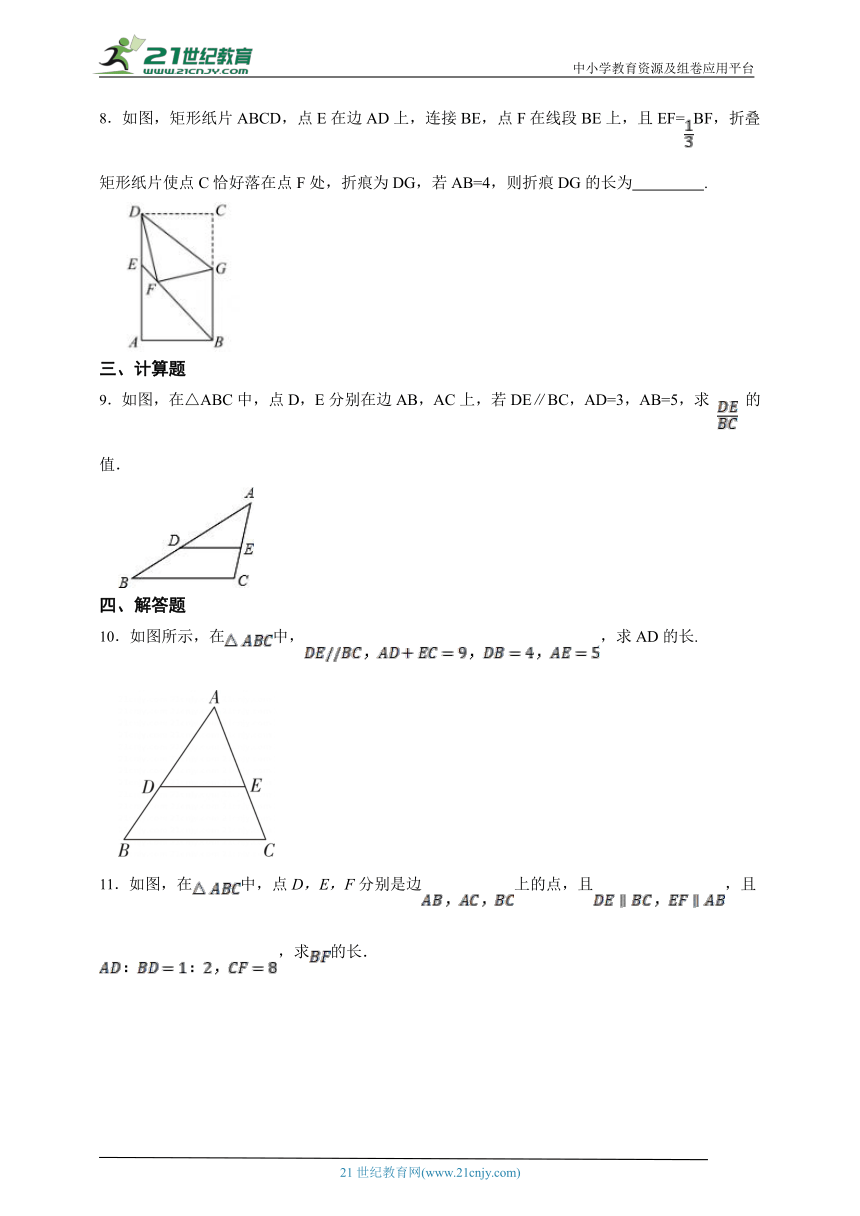
7.如图,在中,,,D是边上一点(点D不与A、B重合).将沿着翻折,点B的对应点为点E,交于点F,如果,则 .
8.如图,矩形纸片ABCD,点E在边AD上,连接BE,点F在线段BE上,且EF=BF,折叠矩形纸片使点C恰好落在点F处,折痕为DG,若AB=4,则折痕DG的长为 .
三、计算题
9.如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,AD=3,AB=5,求 的值.
四、解答题
10.如图所示,在中,,求AD的长.
11.如图,在中,点D,E,F分别是边上的点,且,且,求的长.
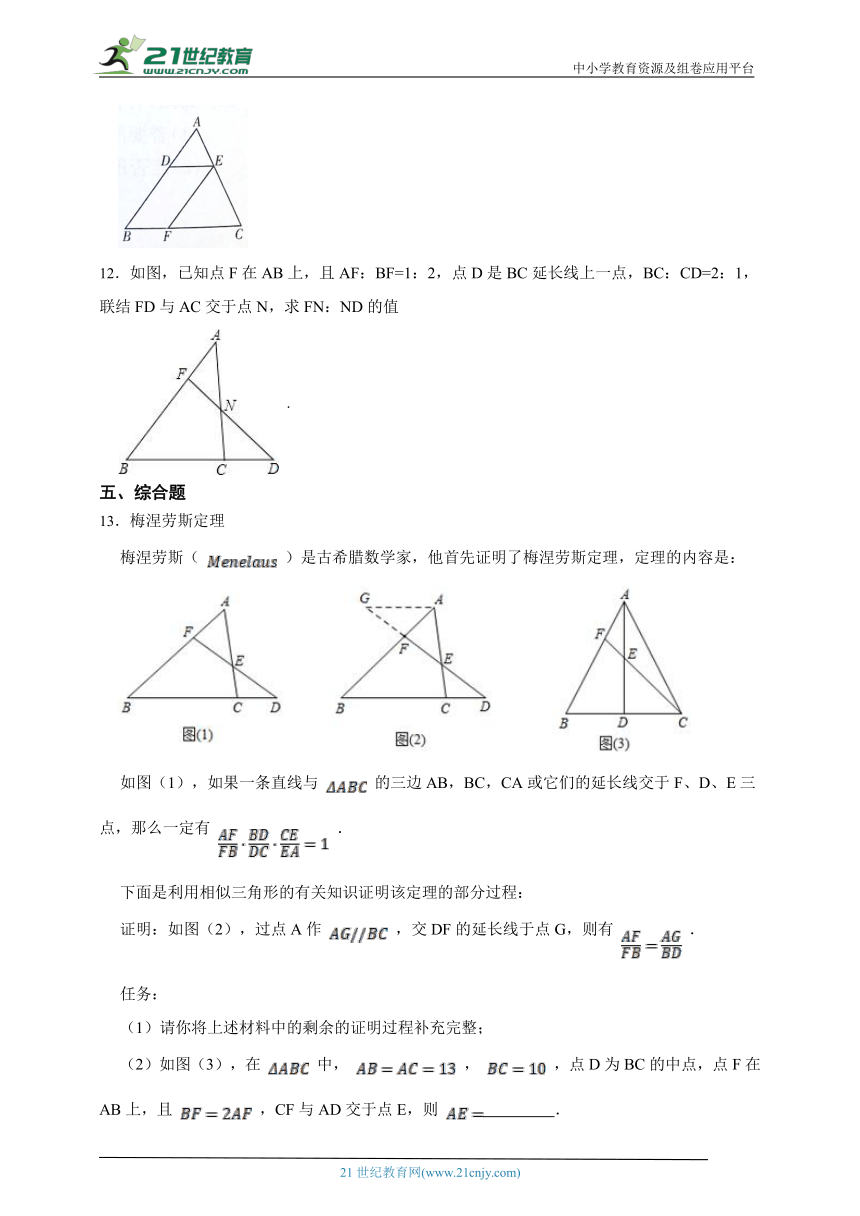
12.如图,已知点F在AB上,且AF:BF=1:2,点D是BC延长线上一点,BC:CD=2:1,联结FD与AC交于点N,求FN:ND的值
.
五、综合题
13.梅涅劳斯定理
梅涅劳斯( )是古希腊数学家,他首先证明了梅涅劳斯定理,定理的内容是:
如图(1),如果一条直线与 的三边AB,BC,CA或它们的延长线交于F、D、E三点,那么一定有 .
下面是利用相似三角形的有关知识证明该定理的部分过程:
证明:如图(2),过点A作 ,交DF的延长线于点G,则有 .
任务:
(1)请你将上述材料中的剩余的证明过程补充完整;
(2)如图(3),在 中, , ,点D为BC的中点,点F在AB上,且 ,CF与AD交于点E,则 .
14.如图,在矩形ABCD中,AB=12,BC=9,点E是射线AD上一动点且以每秒3个单位的速度从A出发向右运动,连结BE交AC于点F,作EM⊥BC于M交直线AC于N,设E点运动时间为1秒.
(1)若将线段EN绕点F旋转后恰好落在直线AB上,则t=
(2)当点E在线段AD上运动时,若FN=5t-3,求t的值.
(3)连结FM,点E在运动过程中,是否存在t的值,使△FMN为等腰三角形?若存在,请求出t的值:若不存在,请说明理由.
六、实践探究题
15.阅读材料解答问题:如图,在菱形ABCD中,AB=AC,过点C作一条直线,分别交AB,AD的延长线于M,N,则
(1)试证明: ;
(2)如图,O为直线AB上一点,OC,OD将平角AOB三等分,点P1,P2,P3分别在射线OA,OD,OB上,0P1=r1,0P2=r2,OP3=r3,r与r′分别满足 ,用直尺在图中分别作出长度r,r′的线段.
16.课本再现
思考我们知道,菱形的对角线互相垂直.反过来,对角线互相垂直的平行四边形是菱形吗 可以发现并证明菱形的一个判定定理:对角线互相垂直的平行四边形是菱形.
(1)定理证明:
为了证明该定理,小明同学画出了图形(如图1),并写出了“已知”和“求证”,请你完成证明过程.已知:在 ABCD中,对角线BD⊥AC,垂足为O.求证: ABCD是菱形.
(2)知识应用:
如图2,在 ABCD中,对角线AC和BD 相交于点O,AD=5,AC=8,BD=6.
①求证: ABCD是菱形.
②延长BC至点E,连结OE交CD于点F,若∠E,求的值.
17.
(1)问题情境:
数学活动课上,小明向同学们提出了这样一个问题:如图(1),在矩形中,分别是的中点,作射线,连接,请直接写出线段与之间的数量关系;
(2)解决问题:
小亮受此问题启发,将矩形变为平行四边形,其中为锐角,如图(2),分别是的中点,过点作交射线于点,交射线于点,连接,则,请你证明小亮的结论;
(3)拓展探究:
小宇在小亮结论的基础上进行了探究,并提出了一个新问题:与有怎样的数量关系?请你回答小宇提出的这个问题,并证明你的结论.
答案解析部分
1.【答案】D
【知识点】平行线分线段成比例
2.【答案】D
【知识点】平行线分线段成比例
3.【答案】D
【知识点】平行线分线段成比例
4.【答案】B
【知识点】平行线分线段成比例
5.【答案】C
【知识点】平行线分线段成比例
6.【答案】4
【知识点】平行线分线段成比例
7.【答案】
【知识点】平行线的性质;等腰三角形的性质;翻折变换(折叠问题);平行线分线段成比例
8.【答案】
【知识点】勾股定理;矩形的性质;翻折变换(折叠问题);平行线分线段成比例
9.【答案】解:∵DE∥BC,
∴ = ,
∵AD=3,AB=5,
∴ =
【知识点】平行线分线段成比例
10.【答案】解:∵DE∥BC,
∴,
∵AD+EC=9,
∴EC=9-AD,
又DB=4,AE=5,
∴
解得AD=4或5.
【知识点】平行线分线段成比例
11.【答案】解:,
.
,
.
,
.
【知识点】平行线分线段成比例
12.【答案】解:过点F作FE∥BD,交AC于点E,∴ ,∵AF:BF=1:2,∴ ,∴ ,即FE= BC,∵BC:CD=2:1,∴CD= BC,∵FE∥BD,∴ .即FN:ND=2:3
【知识点】平行线分线段成比例
13.【答案】(1)解:补充的证明过程如下:
,
,
(2)6
【知识点】平行线分线段成比例;定义新运算
14.【答案】(1)3
(2)解:在Rt△ABC中,
∵EM∥CD,
∴
∴,
∴AF=AN-FN=5t-(5t-3)=3
∵EN∥AB,
∴
∴
解之:.
(3)解:存在,
当0≤t≤3时
在△FMN中,∠MNC<90°,
∴∠FNM>90°,
∵△FMN是等腰三角形,
∴MN=FN;
由(2)可知MN=12-4t,
∵EN∥AB,
∴即
解之:,
∴
解之:t1=2,t2=-2(舍去);
当t>3时,延长MF交AB于点H,
∵∠CMN=90°,
∴∠FMN>90°,
∴FM=MN=EN-EM=4t-12,AN=5t,AE=3t,
∵AB∥EN
∴即
∴
在Rt△HBM中
∴
解之:,(舍去).
∴t的值为2或时△FMN是等腰三角形.
【知识点】等腰三角形的判定;勾股定理;矩形的性质;平行线分线段成比例;旋转的性质
15.【答案】(1)证明:∵四边形ABCD是菱形,
∴BC∥AD,
∴ ,
又∵CD∥AM,
∴ ,
∴ ,
又∵AB=AD=AC,
∴ ;
(2)解:连接P1,P2交OC于点E,则0E=r,
连接EP3交OD于点F,则0F=﹣r′.
【知识点】菱形的性质;平行线分线段成比例
16.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AO=CO,AB=DC,
∵BD⊥AC
∴∠AOB=∠COB=90°,
∵AO=CO,∠AOB=∠COB,BO=BO
∴△AOB≌△COB(SAS),
∴AB=CB,
同理可得△DOA≌△ODC,
则DA=DC,
又∵AB=CD,
∴AB=BC=CD=DA,
∴四边形ABCD是菱形.
(2)证明:①证明:四边形ABCD是平行四边形,AD=5,AC=8,BD=6,
∴,,
在△AOD中,AD2=25,AO2+OD2=32+42=25,
∴AD2=AO2+OD2,
∴△AOD是直角三角形,即∠AOD=90°,
∴AC⊥BD,
∴四边形ABCD是菱形;
②解:如图,过点O作OG∥CD交BC于点G,
∵四边形ABCD是菱形,
∴∠ACB=∠ACD,OC=AO=4,
∵,
∴,
∵∠ACB=∠E+∠COE,
∴∠E=∠COE,
∴,
∵OG∥CD,
则,,
∴,
∴.
【知识点】勾股定理的逆定理;平行四边形的性质;菱形的判定与性质;平行线分线段成比例;三角形全等的判定(SAS)
17.【答案】(1)解:
(2)解:分别是的中点,.
四边形为平行四边形.
四边形为平行四边形即.
如图,连接∵CE⊥AD,N是CD的中点∴CN=EN∴MF垂直平分CE∴ME=MC.
(3)解:∠BME=3∠AEM,证明如下:
∵四边形AMND和四边形ABCD为平行四边形
∴
∴∠AEM=∠EMF,∠NCM=∠BMC.
∵AB=2BC,AB=CD=2CN∴CN=MN∴∠NCM=∠NMC
∴∠BMC=∠NMC∵ME=MC,MF⊥CE∴∠EMF=∠NMC
∴∠BME=∠EMF+∠NMC+∠BMC=3∠EMF=3∠AEM即∠BME=3∠AEM
【知识点】线段垂直平分线的性质;等腰三角形的性质;平行四边形的判定与性质;矩形的性质;平行线分线段成比例;三角形全等的判定(SAS)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【北师大版九上同步练习】
4.2平行线分线断成比例
一、单选题
1.如图,,直线、与这三条平行线分别交于点A、B、C和点D、E、F,,,,则的长是( )
A.8 B.9 C.11 D.12
2.如图,若,则下列各式错误的是( )
A. B. C. D.
3.如图,,点B,E分别在,上,,,的长( )
A.3 B.4 C.5 D.10
4.如图,,,则下列比例式不正确的是( )
A. B. C. D.
5.一段加固后的护栏如图所示,该护栏竖直部分是由等距(任意相邻两根木条之间的距离相等)且平行的木条构成.已知AC=50cm,则BC的长度为( )
A.20cm B.25cm C.30cm D.cm
二、填空题
6.如图,,若,则的长 .
7.如图,在中,,,D是边上一点(点D不与A、B重合).将沿着翻折,点B的对应点为点E,交于点F,如果,则 .
8.如图,矩形纸片ABCD,点E在边AD上,连接BE,点F在线段BE上,且EF=BF,折叠矩形纸片使点C恰好落在点F处,折痕为DG,若AB=4,则折痕DG的长为 .
三、计算题
9.如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,AD=3,AB=5,求 的值.
四、解答题
10.如图所示,在中,,求AD的长.
11.如图,在中,点D,E,F分别是边上的点,且,且,求的长.
12.如图,已知点F在AB上,且AF:BF=1:2,点D是BC延长线上一点,BC:CD=2:1,联结FD与AC交于点N,求FN:ND的值
.
五、综合题
13.梅涅劳斯定理
梅涅劳斯( )是古希腊数学家,他首先证明了梅涅劳斯定理,定理的内容是:
如图(1),如果一条直线与 的三边AB,BC,CA或它们的延长线交于F、D、E三点,那么一定有 .
下面是利用相似三角形的有关知识证明该定理的部分过程:
证明:如图(2),过点A作 ,交DF的延长线于点G,则有 .
任务:
(1)请你将上述材料中的剩余的证明过程补充完整;
(2)如图(3),在 中, , ,点D为BC的中点,点F在AB上,且 ,CF与AD交于点E,则 .
14.如图,在矩形ABCD中,AB=12,BC=9,点E是射线AD上一动点且以每秒3个单位的速度从A出发向右运动,连结BE交AC于点F,作EM⊥BC于M交直线AC于N,设E点运动时间为1秒.
(1)若将线段EN绕点F旋转后恰好落在直线AB上,则t=
(2)当点E在线段AD上运动时,若FN=5t-3,求t的值.
(3)连结FM,点E在运动过程中,是否存在t的值,使△FMN为等腰三角形?若存在,请求出t的值:若不存在,请说明理由.
六、实践探究题
15.阅读材料解答问题:如图,在菱形ABCD中,AB=AC,过点C作一条直线,分别交AB,AD的延长线于M,N,则
(1)试证明: ;
(2)如图,O为直线AB上一点,OC,OD将平角AOB三等分,点P1,P2,P3分别在射线OA,OD,OB上,0P1=r1,0P2=r2,OP3=r3,r与r′分别满足 ,用直尺在图中分别作出长度r,r′的线段.
16.课本再现
思考我们知道,菱形的对角线互相垂直.反过来,对角线互相垂直的平行四边形是菱形吗 可以发现并证明菱形的一个判定定理:对角线互相垂直的平行四边形是菱形.
(1)定理证明:
为了证明该定理,小明同学画出了图形(如图1),并写出了“已知”和“求证”,请你完成证明过程.已知:在 ABCD中,对角线BD⊥AC,垂足为O.求证: ABCD是菱形.
(2)知识应用:
如图2,在 ABCD中,对角线AC和BD 相交于点O,AD=5,AC=8,BD=6.
①求证: ABCD是菱形.
②延长BC至点E,连结OE交CD于点F,若∠E,求的值.
17.
(1)问题情境:
数学活动课上,小明向同学们提出了这样一个问题:如图(1),在矩形中,分别是的中点,作射线,连接,请直接写出线段与之间的数量关系;
(2)解决问题:
小亮受此问题启发,将矩形变为平行四边形,其中为锐角,如图(2),分别是的中点,过点作交射线于点,交射线于点,连接,则,请你证明小亮的结论;
(3)拓展探究:
小宇在小亮结论的基础上进行了探究,并提出了一个新问题:与有怎样的数量关系?请你回答小宇提出的这个问题,并证明你的结论.
答案解析部分
1.【答案】D
【知识点】平行线分线段成比例
2.【答案】D
【知识点】平行线分线段成比例
3.【答案】D
【知识点】平行线分线段成比例
4.【答案】B
【知识点】平行线分线段成比例
5.【答案】C
【知识点】平行线分线段成比例
6.【答案】4
【知识点】平行线分线段成比例
7.【答案】
【知识点】平行线的性质;等腰三角形的性质;翻折变换(折叠问题);平行线分线段成比例
8.【答案】
【知识点】勾股定理;矩形的性质;翻折变换(折叠问题);平行线分线段成比例
9.【答案】解:∵DE∥BC,
∴ = ,
∵AD=3,AB=5,
∴ =
【知识点】平行线分线段成比例
10.【答案】解:∵DE∥BC,
∴,
∵AD+EC=9,
∴EC=9-AD,
又DB=4,AE=5,
∴
解得AD=4或5.
【知识点】平行线分线段成比例
11.【答案】解:,
.
,
.
,
.
【知识点】平行线分线段成比例
12.【答案】解:过点F作FE∥BD,交AC于点E,∴ ,∵AF:BF=1:2,∴ ,∴ ,即FE= BC,∵BC:CD=2:1,∴CD= BC,∵FE∥BD,∴ .即FN:ND=2:3
【知识点】平行线分线段成比例
13.【答案】(1)解:补充的证明过程如下:
,
,
(2)6
【知识点】平行线分线段成比例;定义新运算
14.【答案】(1)3
(2)解:在Rt△ABC中,
∵EM∥CD,
∴
∴,
∴AF=AN-FN=5t-(5t-3)=3
∵EN∥AB,
∴
∴
解之:.
(3)解:存在,
当0≤t≤3时
在△FMN中,∠MNC<90°,
∴∠FNM>90°,
∵△FMN是等腰三角形,
∴MN=FN;
由(2)可知MN=12-4t,
∵EN∥AB,
∴即
解之:,
∴
解之:t1=2,t2=-2(舍去);
当t>3时,延长MF交AB于点H,
∵∠CMN=90°,
∴∠FMN>90°,
∴FM=MN=EN-EM=4t-12,AN=5t,AE=3t,
∵AB∥EN
∴即
∴
在Rt△HBM中
∴
解之:,(舍去).
∴t的值为2或时△FMN是等腰三角形.
【知识点】等腰三角形的判定;勾股定理;矩形的性质;平行线分线段成比例;旋转的性质
15.【答案】(1)证明:∵四边形ABCD是菱形,
∴BC∥AD,
∴ ,
又∵CD∥AM,
∴ ,
∴ ,
又∵AB=AD=AC,
∴ ;
(2)解:连接P1,P2交OC于点E,则0E=r,
连接EP3交OD于点F,则0F=﹣r′.
【知识点】菱形的性质;平行线分线段成比例
16.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AO=CO,AB=DC,
∵BD⊥AC
∴∠AOB=∠COB=90°,
∵AO=CO,∠AOB=∠COB,BO=BO
∴△AOB≌△COB(SAS),
∴AB=CB,
同理可得△DOA≌△ODC,
则DA=DC,
又∵AB=CD,
∴AB=BC=CD=DA,
∴四边形ABCD是菱形.
(2)证明:①证明:四边形ABCD是平行四边形,AD=5,AC=8,BD=6,
∴,,
在△AOD中,AD2=25,AO2+OD2=32+42=25,
∴AD2=AO2+OD2,
∴△AOD是直角三角形,即∠AOD=90°,
∴AC⊥BD,
∴四边形ABCD是菱形;
②解:如图,过点O作OG∥CD交BC于点G,
∵四边形ABCD是菱形,
∴∠ACB=∠ACD,OC=AO=4,
∵,
∴,
∵∠ACB=∠E+∠COE,
∴∠E=∠COE,
∴,
∵OG∥CD,
则,,
∴,
∴.
【知识点】勾股定理的逆定理;平行四边形的性质;菱形的判定与性质;平行线分线段成比例;三角形全等的判定(SAS)
17.【答案】(1)解:
(2)解:分别是的中点,.
四边形为平行四边形.
四边形为平行四边形即.
如图,连接∵CE⊥AD,N是CD的中点∴CN=EN∴MF垂直平分CE∴ME=MC.
(3)解:∠BME=3∠AEM,证明如下:
∵四边形AMND和四边形ABCD为平行四边形
∴
∴∠AEM=∠EMF,∠NCM=∠BMC.
∵AB=2BC,AB=CD=2CN∴CN=MN∴∠NCM=∠NMC
∴∠BMC=∠NMC∵ME=MC,MF⊥CE∴∠EMF=∠NMC
∴∠BME=∠EMF+∠NMC+∠BMC=3∠EMF=3∠AEM即∠BME=3∠AEM
【知识点】线段垂直平分线的性质;等腰三角形的性质;平行四边形的判定与性质;矩形的性质;平行线分线段成比例;三角形全等的判定(SAS)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
