【北师大版九上同步练习】 4.4 探索三角形相似的条件(含答案)
文档属性
| 名称 | 【北师大版九上同步练习】 4.4 探索三角形相似的条件(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-11 16:16:28 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
【北师大版九上同步练习】
4.4探索三角形相似的条件
一、单选题
1.黄金分割由于其美学性质,受到摄影爱好者和艺术家的喜爱,摄影中有一种拍摄手法叫黄金构图法,其原理是:如图,将正方形ABCD的底边BC取中点E,以E为圆心,线段DE为半径作圆,其与底边BC的延长线交于点F,这样就把正方形ABCD延伸为矩形ABFG,称其为黄金矩形,若CF=4a,则AB=( ).
A.(﹣1)a B.(2﹣2)a C.(+1)a D.(2+2)a
2.若P是线段AB的黄金分割点,且AP>BP,若AP=4-4,则线段AB的长为( )
A.2 B.4 C.6 D.8
3.如图,是著名画家达·芬奇的名画《蒙娜丽莎》.画中的脸部被包在矩形ABCD内,点E是AB的黄金分割点,BE>AE,若AB=2,则BE长为( )
A. B. C. D.
4.如图,在四边形ABCD中,已知∠ADC=∠BAC,那么补充下列条件后不能判定△ADC和△BAC相似的是( )
A.CA平分∠BCD B.∠DAC=∠ABC
C.AC2=BC CD D.
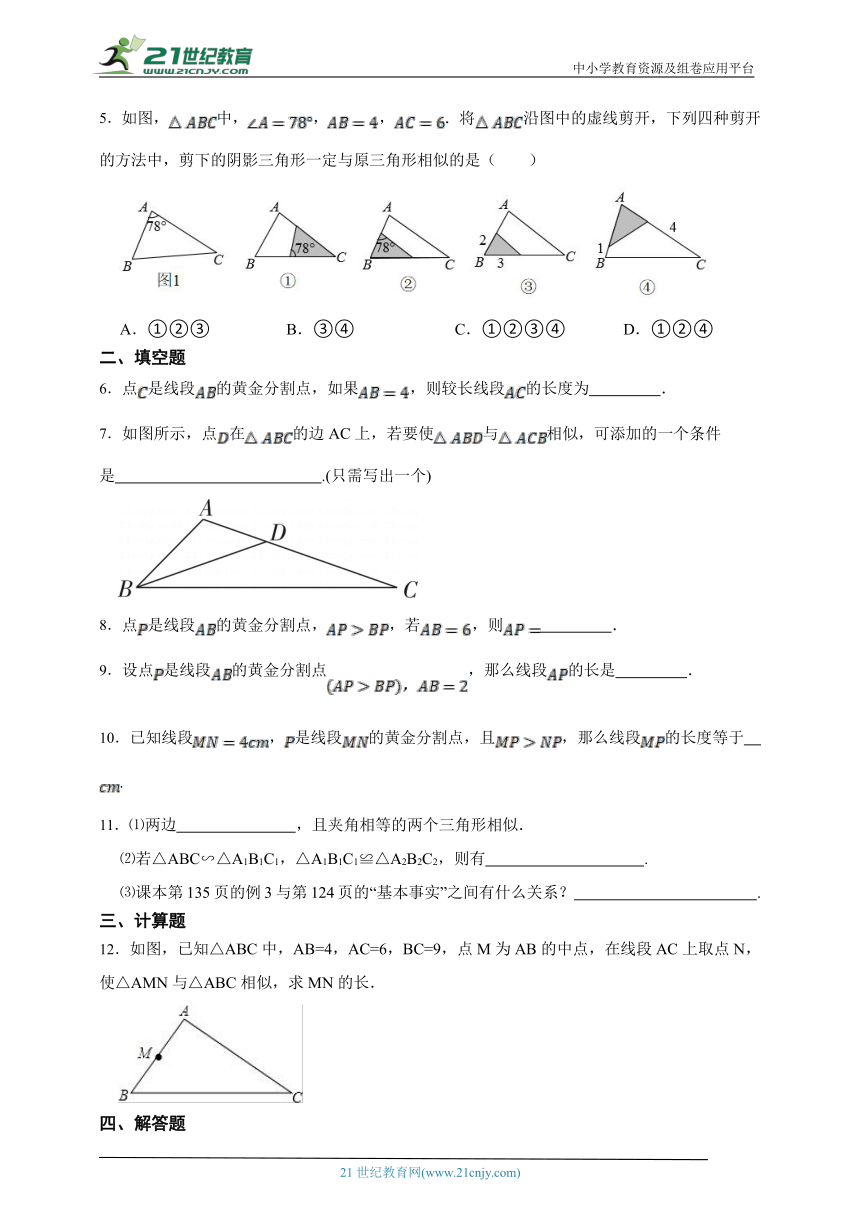
5.如图,中,,,.将沿图中的虚线剪开,下列四种剪开的方法中,剪下的阴影三角形一定与原三角形相似的是( )
A.①②③ B.③④ C.①②③④ D.①②④
二、填空题
6.点是线段的黄金分割点,如果,则较长线段的长度为 .
7.如图所示,点在的边AC上,若要使与相似,可添加的一个条件是 .(只需写出一个)
8.点是线段的黄金分割点,,若,则 .
9.设点是线段的黄金分割点,那么线段的长是 .
10.已知线段,是线段的黄金分割点,且,那么线段的长度等于 .
11.⑴两边 ,且夹角相等的两个三角形相似.
⑵若△ABC∽△A1B1C1,△A1B1C1≌△A2B2C2,则有 .
⑶课本第135页的例3与第124页的“基本事实”之间有什么关系? .
三、计算题
12.如图,已知△ABC中,AB=4,AC=6,BC=9,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求MN的长.
四、解答题
13.如图,在△ABC和OACD中,AD⊥CD于点D,AC⊥BC于点C.请再添加一个条件,使△ABC∽△CAD,并加以证明.
答案解析部分
1.【答案】D
【知识点】勾股定理;正方形的性质;黄金分割
2.【答案】D
【知识点】黄金分割
3.【答案】B
【知识点】黄金分割
4.【答案】C
【知识点】相似三角形的判定
5.【答案】D
【知识点】相似三角形的判定
6.【答案】
【知识点】黄金分割
7.【答案】(答案不 一)
【知识点】相似三角形的判定
8.【答案】
【知识点】黄金分割
9.【答案】
【知识点】黄金分割
10.【答案】
【知识点】黄金分割
11.【答案】对应成比例;△ABC∽△A2B2C2;两个命题是互逆关系
【知识点】相似三角形的判定
12.【答案】解:∵△ABC中,AB=4,点M为AB的中点,
∴AM=2.
当△AMN∽△ABC时, = ,即 = ,解得MN= ;
当△AMN∽△ACB时, = ,即 = ,解得MN=3.
∴MN的长为: 或3
【知识点】相似三角形的判定
13.【答案】添加条件:AB∥CD.
证明:∵AD⊥CD,AC⊥BC,
∴∠ADC=∠ACB=90°,
∵AB∥CD,
∴∠CAB=∠DCA
∴△ABC∽△CAD.
【知识点】相似三角形的判定
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【北师大版九上同步练习】
4.4探索三角形相似的条件
一、单选题
1.黄金分割由于其美学性质,受到摄影爱好者和艺术家的喜爱,摄影中有一种拍摄手法叫黄金构图法,其原理是:如图,将正方形ABCD的底边BC取中点E,以E为圆心,线段DE为半径作圆,其与底边BC的延长线交于点F,这样就把正方形ABCD延伸为矩形ABFG,称其为黄金矩形,若CF=4a,则AB=( ).
A.(﹣1)a B.(2﹣2)a C.(+1)a D.(2+2)a
2.若P是线段AB的黄金分割点,且AP>BP,若AP=4-4,则线段AB的长为( )
A.2 B.4 C.6 D.8
3.如图,是著名画家达·芬奇的名画《蒙娜丽莎》.画中的脸部被包在矩形ABCD内,点E是AB的黄金分割点,BE>AE,若AB=2,则BE长为( )
A. B. C. D.
4.如图,在四边形ABCD中,已知∠ADC=∠BAC,那么补充下列条件后不能判定△ADC和△BAC相似的是( )
A.CA平分∠BCD B.∠DAC=∠ABC
C.AC2=BC CD D.
5.如图,中,,,.将沿图中的虚线剪开,下列四种剪开的方法中,剪下的阴影三角形一定与原三角形相似的是( )
A.①②③ B.③④ C.①②③④ D.①②④
二、填空题
6.点是线段的黄金分割点,如果,则较长线段的长度为 .
7.如图所示,点在的边AC上,若要使与相似,可添加的一个条件是 .(只需写出一个)
8.点是线段的黄金分割点,,若,则 .
9.设点是线段的黄金分割点,那么线段的长是 .
10.已知线段,是线段的黄金分割点,且,那么线段的长度等于 .
11.⑴两边 ,且夹角相等的两个三角形相似.
⑵若△ABC∽△A1B1C1,△A1B1C1≌△A2B2C2,则有 .
⑶课本第135页的例3与第124页的“基本事实”之间有什么关系? .
三、计算题
12.如图,已知△ABC中,AB=4,AC=6,BC=9,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求MN的长.
四、解答题
13.如图,在△ABC和OACD中,AD⊥CD于点D,AC⊥BC于点C.请再添加一个条件,使△ABC∽△CAD,并加以证明.
答案解析部分
1.【答案】D
【知识点】勾股定理;正方形的性质;黄金分割
2.【答案】D
【知识点】黄金分割
3.【答案】B
【知识点】黄金分割
4.【答案】C
【知识点】相似三角形的判定
5.【答案】D
【知识点】相似三角形的判定
6.【答案】
【知识点】黄金分割
7.【答案】(答案不 一)
【知识点】相似三角形的判定
8.【答案】
【知识点】黄金分割
9.【答案】
【知识点】黄金分割
10.【答案】
【知识点】黄金分割
11.【答案】对应成比例;△ABC∽△A2B2C2;两个命题是互逆关系
【知识点】相似三角形的判定
12.【答案】解:∵△ABC中,AB=4,点M为AB的中点,
∴AM=2.
当△AMN∽△ABC时, = ,即 = ,解得MN= ;
当△AMN∽△ACB时, = ,即 = ,解得MN=3.
∴MN的长为: 或3
【知识点】相似三角形的判定
13.【答案】添加条件:AB∥CD.
证明:∵AD⊥CD,AC⊥BC,
∴∠ADC=∠ACB=90°,
∵AB∥CD,
∴∠CAB=∠DCA
∴△ABC∽△CAD.
【知识点】相似三角形的判定
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
