第二十二章 二次函数单元测试卷(含答案)
文档属性
| 名称 | 第二十二章 二次函数单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 475.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-11 15:49:08 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025人教版九年级数学上册
第二十二章 二次函数
时间 90分钟 满分 100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.用配方法将二次函数y=x2+8x-9化成顶点式的形式,下列正确的为 ( )
A.y=(x-4)2+7 B.y=(x-4)2-25
C.y=(x+4)2+7 D.y=(x+4)2-25
2.(2022·北京西城区期中)已知y=(m+2)x|m|+2是y关于x的二次函数,那么m的值为 ( )
A.2 B.-2 C.±2 D.±1
3.(2023·北京昌平区期末)关于四个函数y=-2x2,y=x2,y=3x2,y=-x2的共同点,下列说法正确的是 ( )
A.图象开口向上 B.图象有最低点
C.图象对称轴是y轴 D.y随x增大而增大
4.(2023·福州鼓楼区期末)已知二次函数y=x2-bx+c的图象经过A(1,n),B(3,n),则b的值为 ( )
A.2 B.-2 C.4 D.-4
5.(2022·浙江湖州期中)已知抛物线y=(x-3)2+c经过点A(2,0),则该抛物线与x轴的另一个交点坐标为 ( )
A.(3,0) B.(-4,0)
C.(-8,0) D.(4,0)
6.(2023·河北石家庄期末)已知二次函数y=-x2+bx+c的图象如图所示,并有以下结论:①函数图象与y轴正半轴相交;②当x<0时,y随x的增大而增大,则坐标系的原点O可能是( )
A.点A B.点B C.点C D.点D
7.若二次函数y=x2-6x+5,当2≤x≤6时,y的最大值是n,最小值是m,则n-m=( )
A.3 B.5 C.7 D.9
8.(2023·合肥庐阳区期中)2022年9月29日国产大飞机C919获得型号合格证,
这标志着我国具备了按照国际通行适航标准研制大型客机的能力.如果某型号飞
机降落后滑行的距离s(单位:米)关于滑行的时间t(单位:秒)的函数解析式是s=
54t-t2,则该飞机着陆后滑行的最长时间为( )
A.243秒 B.486秒 C.18秒 D.36秒
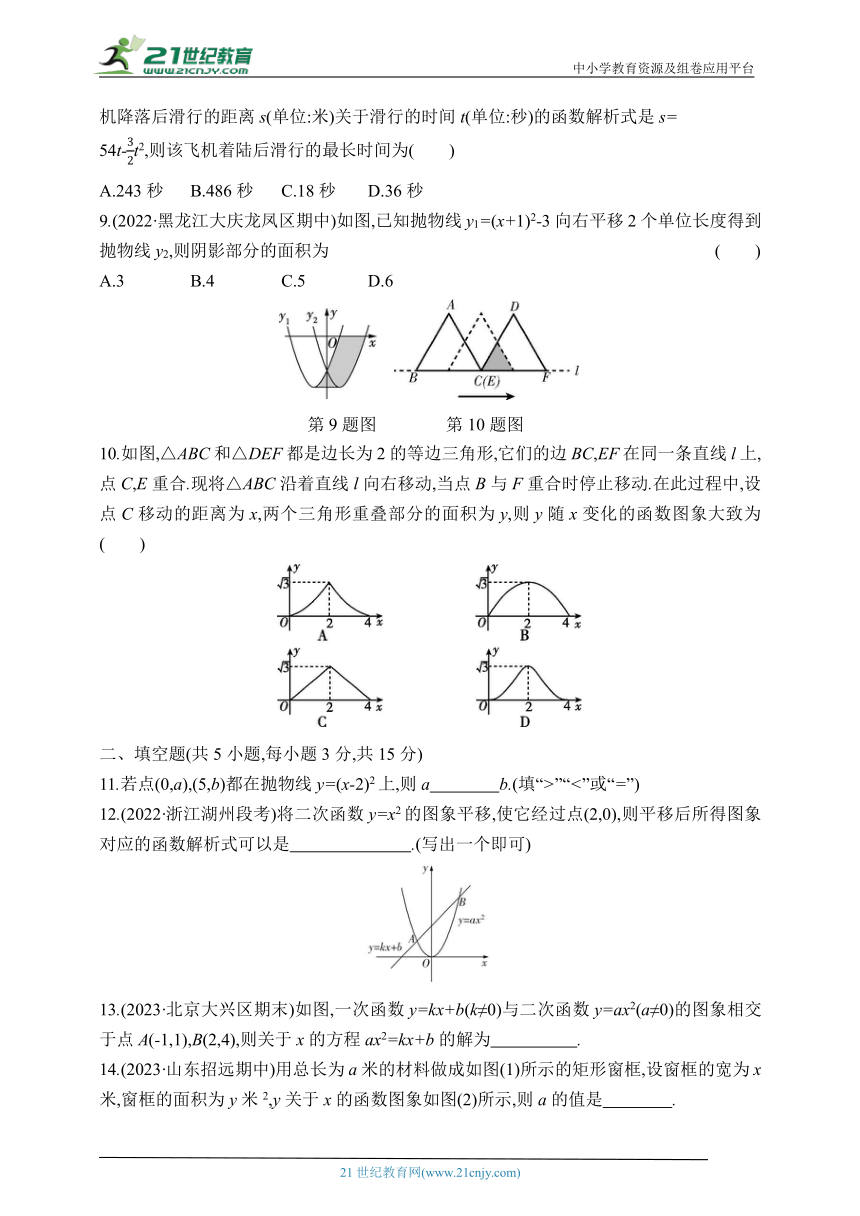
9.(2022·黑龙江大庆龙凤区期中)如图,已知抛物线y1=(x+1)2-3向右平移2个单位长度得到抛物线y2,则阴影部分的面积为 ( )
A.3 B.4 C.5 D.6
第9题图 第10题图
10.如图,△ABC和△DEF都是边长为2的等边三角形,它们的边BC,EF在同一条直线l上,点C,E重合.现将△ABC沿着直线l向右移动,当点B与F重合时停止移动.在此过程中,设点C移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
二、填空题(共5小题,每小题3分,共15分)
11.若点(0,a),(5,b)都在抛物线y=(x-2)2上,则a b.(填“>”“<”或“=”)
12.(2022·浙江湖州段考)将二次函数y=x2的图象平移,使它经过点(2,0),则平移后所得图象对应的函数解析式可以是 .(写出一个即可)
13.(2023·北京大兴区期末)如图,一次函数y=kx+b(k≠0)与二次函数y=ax2(a≠0)的图象相交于点A(-1,1),B(2,4),则关于x的方程ax2=kx+b的解为 .
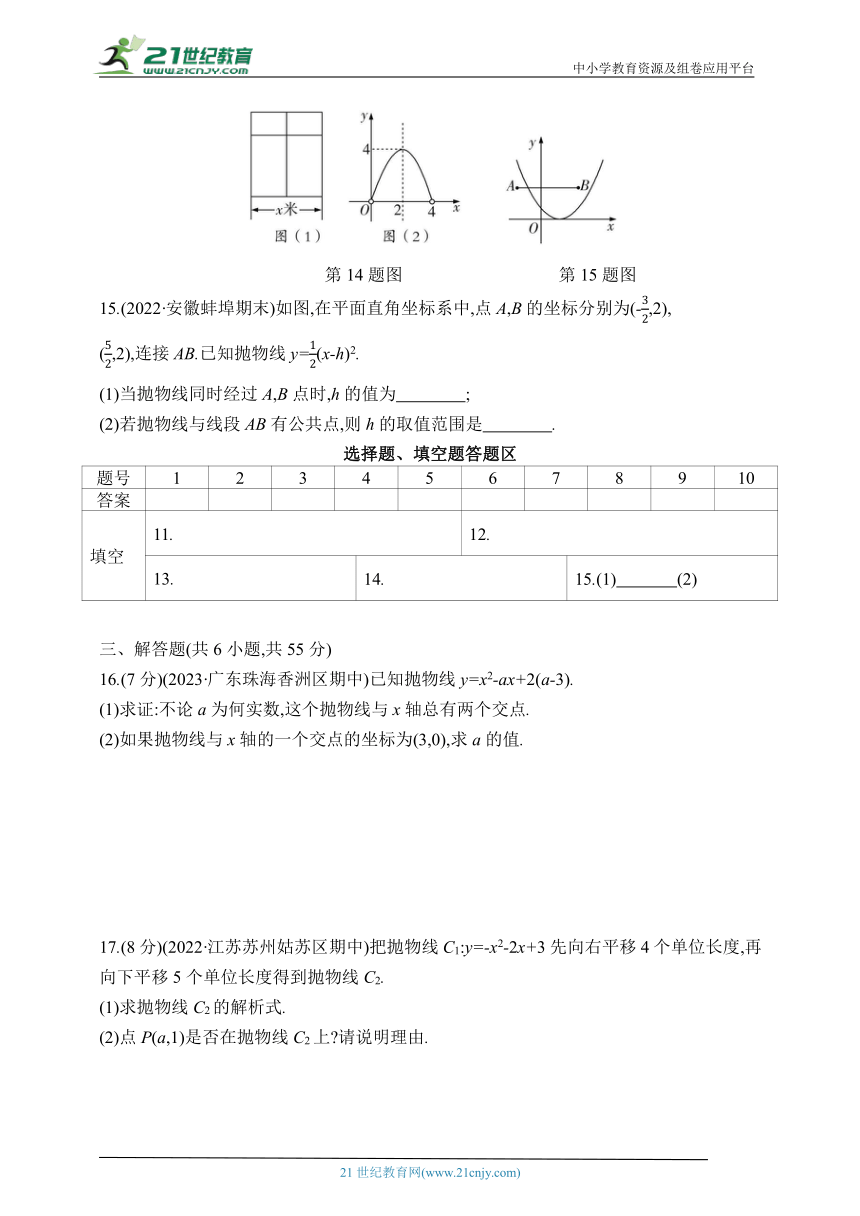
14.(2023·山东招远期中)用总长为a米的材料做成如图(1)所示的矩形窗框,设窗框的宽为x米,窗框的面积为y米2,y关于x的函数图象如图(2)所示,则a的值是 .
第14题图 第15题图
15.(2022·安徽蚌埠期末)如图,在平面直角坐标系中,点A,B的坐标分别为(-,2),
(,2),连接AB.已知抛物线y=(x-h)2.
(1)当抛物线同时经过A,B点时,h的值为 ;
(2)若抛物线与线段AB有公共点,则h的取值范围是 .
选择题、填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12.
13. 14. 15.(1) (2)
三、解答题(共6小题,共55分)
16.(7分)(2023·广东珠海香洲区期中)已知抛物线y=x2-ax+2(a-3).
(1)求证:不论a为何实数,这个抛物线与x轴总有两个交点.
(2)如果抛物线与x轴的一个交点的坐标为(3,0),求a的值.
17.(8分)(2022·江苏苏州姑苏区期中)把抛物线C1:y=-x2-2x+3先向右平移4个单位长度,再向下平移5个单位长度得到抛物线C2.
(1)求抛物线C2的解析式.
(2)点P(a,1)是否在抛物线C2上 请说明理由.
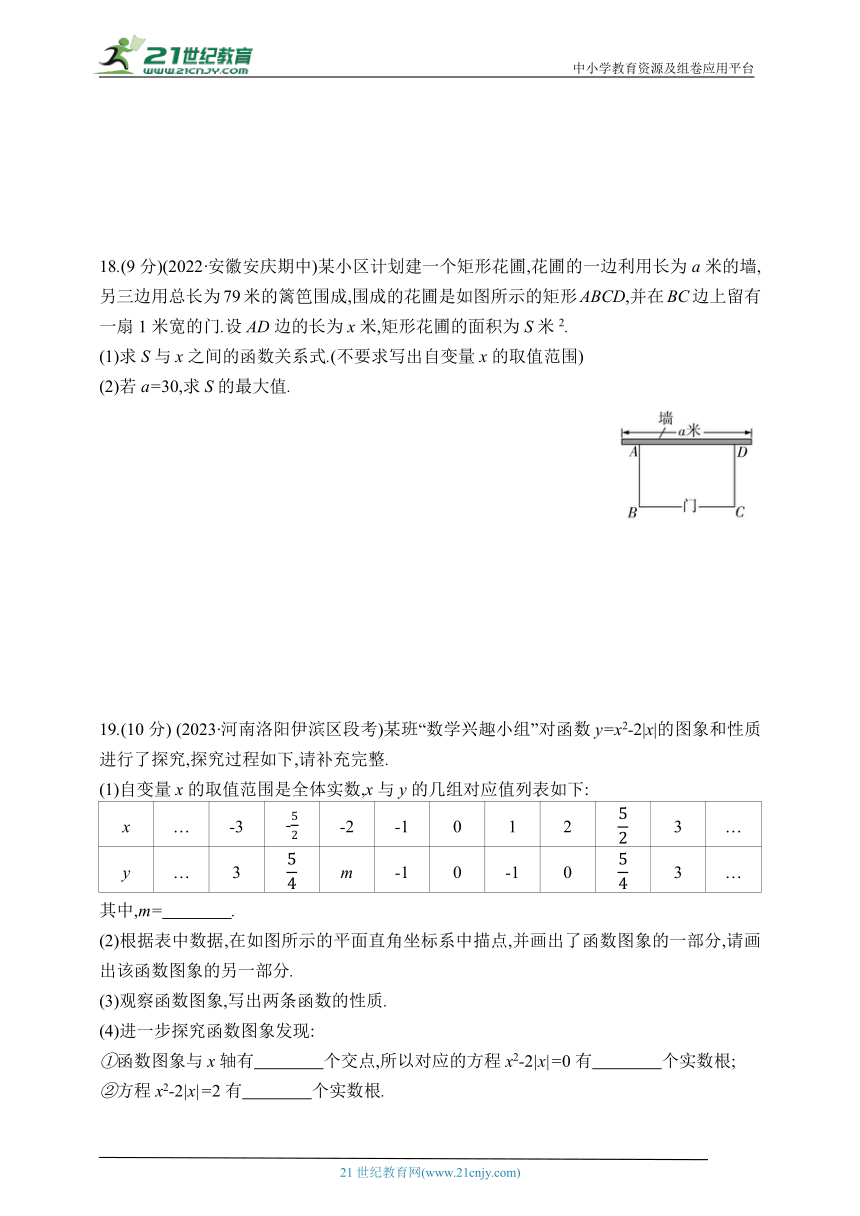
18.(9分)(2022·安徽安庆期中)某小区计划建一个矩形花圃,花圃的一边利用长为a米的墙,另三边用总长为79米的篱笆围成,围成的花圃是如图所示的矩形ABCD,并在BC边上留有一扇1米宽的门.设AD边的长为x米,矩形花圃的面积为S米2.
(1)求S与x之间的函数关系式.(不要求写出自变量x的取值范围)
(2)若a=30,求S的最大值.
19.(10分) (2023·河南洛阳伊滨区段考)某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x … -3 - -2 -1 0 1 2 3 …
y … 3 m -1 0 -1 0 3 …
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2-2|x|=0有 个实数根;
②方程x2-2|x|=2有 个实数根.
20.(10分)(2023·浙江绍兴越城区期中)商店以每件40元的价格购进一种商品,经
市场调查发现:在一段时间内,该商品的日销售量y(件)与售价x(元/件)成一次函数
关系,其对应关系如表.
售价/(元/件) 45 50 60
日销售量/件 110 100 80
(1)求y关于x的函数表达式.
(2)求售价为多少时,日销售利润w最大,最大利润是多少元.
(3)该商店准备搞节日促销活动,顾客每购买一件该商品奖m元(m>0),若在日销售量
不少于68件时的日销售最大利润是1 360元,且日销售量与售价仍然满足(1)中的函数关系式,求m的值.(每件的销售利润=售价-进价)
21.(11分)如图,在平面直角坐标系xOy中,已知抛物线y=-x2+2x+3与x轴交于A,B两点,与y轴交于点D,抛物线的顶点为E,且C,D两点关于抛物线的对称轴对称,直线y=kx+b经过A,C两点.
(1)求直线AC的解析式.
(2)设点P是直线AC上方抛物线上的一动点,当△PAC的面积取得最大值时,求出此时点P的坐标.
(3)若点M在此抛物线上,点N在抛物线的对称轴上,则以A,C,M,N为顶点的四边形能否构成以AC为边的平行四边形 若能,请直接写出所有满足要求的点M的坐标;若不能,请说明理由.
第二十二章 二次函数
选择题、填空题答案速查
1 2 3 4 5 6 7 8 9 10
D A C C D B D C D A
11.< 12.y=x2-4(或y=x2-4x+4,答案不唯一) 13.x1=-1,x2=2
14.12 15.(1) (2)-≤h≤
1.D y=x2+8x-9=x2+8x+16-9-16=(x+4) 2-25.
2.A ∵y=(m+2)x|m|+2是y关于x的二次函数,∴|m|=2且m+2≠0,解得m=2.
3.C 分析如下:
y=-2x2 图象开口向下 图象有最高点 图象对称轴是y轴 当x>0时,y随x的增大而减小,当x<0时,y随x的增大而增大
y=x2 图象开口向上 图象有最低点 图象对称轴是y轴 当x>0时,y随x的增大而增大,当x<0时,y随x的增大而减小
y=3x2 图象开口向上 图象有最低点 图象对称轴是y轴 当x>0时,y随x的增大而增大,当x<0时,y随x的增大而减小
y=-x2 图象开口向下 图象有最高点 图象对称轴是y轴 当x>0时,y随x的增大而减小,当x<0时,y随x的增大而增大
4.C ∵抛物线经过点A(1,n)和点B(3,n),∴抛物线的对称轴为直线x==2,即-=2,解得b=4.
5.D ∵抛物线y=(x-3)2+c经过点A(2,0),∴(2-3)2+c=0,解得c=-1.∴抛物线的解析式为y=(x-3)2-1.令y=0,即(x-3)2-1=0.解得x=2或x=4.∴该抛物线与x轴的另一个交点坐标为(4,0).
∵抛物线的对称轴为直线x=3,抛物线与x轴的一个交点坐标为(2,0),∴由抛物线的对称性可知,抛物线与x轴的另一个交点坐标为(4,0).
6.B ∵函数图象与y轴正半轴相交,∴y轴在抛物线与x轴的两个交点之间,∴点B,C可能是原点.∵当x<0时,y随x的增大而增大,∴y轴在抛物线顶点左侧,∴点B可能是原点.
7.D 原式可化为y=(x-3)2-4,可知二次函数图象的顶点坐标为(3,-4).因为2<3<6,所以最小值m=-4.当y=0时,x2-6x+5=0,解得x1=1,x2=5.如图,当x=6时,y=36-36+5=5,即n=5.则n-m=5-(-4)=9.
8.C s=54t-t2=-(t-18)2+486,∵-<0,抛物线开口向下,∴当t=18时,s取得最大值,此时s=486.∵飞机滑行到最大距离时停下来,此时滑行时间也为最大值,∴t=18.
9.D (转化思想)如图,设点M为抛物线y1的顶点,点N为抛物线y2的顶点,连接MA,
NB,则四边形AMNB的面积和阴影部分的面积相等.由题意得AB∥MN,AB=MN=2,∴四边形AMNB是平行四边形.∵抛物线y1=(x+1)2-3,∴顶点M的坐标为(-1,-3),∴点M到x轴的距离为3,∴平行四边形AMNB的面积是2×3=6,∴阴影部分的面积是6.
10.A (分类讨论思想)当0 图(1) 图(2)
11.<
12.y=x2-4(或y=x2-4x+4,答案不唯一) 设二次函数y=x2的图象沿y轴平移后得到y=x2+b的图象.∵经过点(2,0),∴0=4+b,解得b=-4,∴沿y轴平移后所得图象对应的函数解析式是y=x2-4.设二次函数y=x2的图象沿x轴平移后得到y=(x-a)2的图象,将(2,0)代入,解得a=2,∴沿x轴平移后所得图象对应的函数解析式是y=(x-2)2=x2-
4x+4.
13.x1=-1,x2=2 ∵一次函数y=kx+b(k≠0)与二次函数y=ax2(a≠0)的图象相交于点A(-1,1),B(2,4),∴关于x的方程ax2=kx+b的解为x1=-1,x2=2.
14.12 由图象可知,当x=2时,y取得最大值,且最大值为4,∴窗框的最大面积是4米2.根据矩形面积计算公式,得窗框的另一边的长为4÷2=2(米),∴材料总长a=
3×2+3×2=12(米).
15.(1) (2)-≤h≤ (1)易知抛物线y=(x-h)2的对称轴为直线x=h,当抛物线同时经过点A(-,2),B(,2)时,抛物线的对称轴为直线x==,∴h=.(2)当抛物线经过A点时,可得2=(--h)2,解得h=-或;当抛物线经过B点时,可得2=(-h)2,解得h=或.故抛物线与线段AB有公共点,则h的取值范围是-≤h≤.
16.【参考答案】(1)证明:Δ=a2-8(a-3)=a2-8a+24=a2-8a+16+8=(a-4)2+8>0,
则不论a为何实数,这个抛物线与x轴总有两个交点. (4分)
(2)把(3,0)代入得9-3a+2(a-3)=0,
解得a=3. (7分)
17.【参考答案】(1)∵y=-x2-2x+3=-(x+1)2+4,
∴把抛物线C1:y=-x2-2x+3先向右平移4个单位长度,再向下平移5个单位长度得到抛物线C2:y=-(x+1-4)2+4-5,即y=-(x-3)2-1, (3分)
∴抛物线C2的解析式为y=-(x-3)2-1. (4分)
(2)不在. (5分)
理由:∵抛物线C2的解析式为y=-(x-3)2-1,
∴该函数的最大值为-1. (7分)
∵点P的纵坐标为1,且1>-1,
∴点P(a,1)不在抛物线C2上. (8分)
18.【参考答案】(1)AB边的长为=(40-x)(米),
根据题意得S=(40-x)x=-x2+40x, (3分)
∴S与x之间的函数关系式为S=-x2+40x. (4分)
(2)由(1)知S=-x2+40x=-(x-40)2+800,(5分)
∵-<0,
∴当x≤40时,S随x的增大而增大.
∵x≤a,a=30,
∴当x=30时,S取得最大值,最大值为750.(9分)
19.【参考答案】(1)0 (2分)
解法提示:把x=-2代入y=x2-2|x|,得y=0,
所以m=0.
(2)如图所示.
(5分)
(3)①函数y=x2-2|x|的图象关于y轴对称;
②当x>1时,y随x的增大而增大.(答案不唯一)(7分)
(4)①3 3 (9分)
②2 (10分)
20.【参考答案】(1)设y关于x的函数关系式为y=kx+b,
由题意得
解得
故y关于x的函数关系式是y=-2x+200(40(2)日销售利润w=(x-40)y=(x-40)(-2x+200)=-2(x-70)2+1 800,
故当售价是70元/件时,日销售利润w最大,最大利润是1 800元. (6分)
(3)由题意得-2x+200≥68,
∴x≤66,
∴日销量利润w=(-2x+200)(x-40-m)=-2x2+(2m+280)x-8 000-200m(40∵m>0,
∴>70.
∵-2<0,
∴w关于x的函数的图象所在的抛物线开口向下,对称轴为直线x=.
∵x≤66<70,
∴w随x的增大而增大,
∴当x=66时,w取得最大值,最大值为(-2×66+200)(66-40-m)=68(26-m),
∴68(26-m)=1 360,
∴m=6. (10分)
21.【参考答案】(1)对于y=-x2+2x+3,令x=0,则y=3,
令-x2+2x+3=0,解得x=-1或3,
故点A,B,D的坐标分别为(-1,0),(3,0),(0,3),抛物线的对称轴为直线x=1. (2分)
∵C,D两点关于抛物线的对称轴x=1对称,D(0,3),
∴C(2,3).
将点A,C的坐标分别代入y=kx+b,得解得
故直线AC的解析式为y=x+1. (4分)
(2)如图,过点P作y轴的平行线交AC于点H. (5分)
设P(t,-t2+2t+3),则H(t,t+1),
S△PAC=S△PHA+S△PHC=PH·(xC-xA).
∵A,C点的位置已确定,
∴当PH的值最大时,S△PAC最大.
PH=-t2+2t+3-t-1=-t2+t+2,
∵-1<0,
∴当t=-=时,△PAC的面积取得最大值,
此时点P的纵坐标为-()2+2×+3=,
故点P的坐标为(,). (8分)
(3)点M的坐标为(-2,-5)或(4,-5). (11分)
(3)解法提示:画示意图如图所示,
∵A(-1,0),C(2,3),
∴点A,C之间的水平距离为3.
∵平行四边形以AC为边,
∴由平行四边形的性质知,点M,N的水平距离为3.
又点N在对称轴x=1上,
∴点N的横坐标为1,
∴点M的横坐标为-2或4.
∵点M在抛物线上,
∴将点M的横坐标代入即可得点M的坐标为(-2,-5)或(4,-5).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教版九年级数学上册
第二十二章 二次函数
时间 90分钟 满分 100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.用配方法将二次函数y=x2+8x-9化成顶点式的形式,下列正确的为 ( )
A.y=(x-4)2+7 B.y=(x-4)2-25
C.y=(x+4)2+7 D.y=(x+4)2-25
2.(2022·北京西城区期中)已知y=(m+2)x|m|+2是y关于x的二次函数,那么m的值为 ( )
A.2 B.-2 C.±2 D.±1
3.(2023·北京昌平区期末)关于四个函数y=-2x2,y=x2,y=3x2,y=-x2的共同点,下列说法正确的是 ( )
A.图象开口向上 B.图象有最低点
C.图象对称轴是y轴 D.y随x增大而增大
4.(2023·福州鼓楼区期末)已知二次函数y=x2-bx+c的图象经过A(1,n),B(3,n),则b的值为 ( )
A.2 B.-2 C.4 D.-4
5.(2022·浙江湖州期中)已知抛物线y=(x-3)2+c经过点A(2,0),则该抛物线与x轴的另一个交点坐标为 ( )
A.(3,0) B.(-4,0)
C.(-8,0) D.(4,0)
6.(2023·河北石家庄期末)已知二次函数y=-x2+bx+c的图象如图所示,并有以下结论:①函数图象与y轴正半轴相交;②当x<0时,y随x的增大而增大,则坐标系的原点O可能是( )
A.点A B.点B C.点C D.点D
7.若二次函数y=x2-6x+5,当2≤x≤6时,y的最大值是n,最小值是m,则n-m=( )
A.3 B.5 C.7 D.9
8.(2023·合肥庐阳区期中)2022年9月29日国产大飞机C919获得型号合格证,
这标志着我国具备了按照国际通行适航标准研制大型客机的能力.如果某型号飞
机降落后滑行的距离s(单位:米)关于滑行的时间t(单位:秒)的函数解析式是s=
54t-t2,则该飞机着陆后滑行的最长时间为( )
A.243秒 B.486秒 C.18秒 D.36秒
9.(2022·黑龙江大庆龙凤区期中)如图,已知抛物线y1=(x+1)2-3向右平移2个单位长度得到抛物线y2,则阴影部分的面积为 ( )
A.3 B.4 C.5 D.6
第9题图 第10题图
10.如图,△ABC和△DEF都是边长为2的等边三角形,它们的边BC,EF在同一条直线l上,点C,E重合.现将△ABC沿着直线l向右移动,当点B与F重合时停止移动.在此过程中,设点C移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
二、填空题(共5小题,每小题3分,共15分)
11.若点(0,a),(5,b)都在抛物线y=(x-2)2上,则a b.(填“>”“<”或“=”)
12.(2022·浙江湖州段考)将二次函数y=x2的图象平移,使它经过点(2,0),则平移后所得图象对应的函数解析式可以是 .(写出一个即可)
13.(2023·北京大兴区期末)如图,一次函数y=kx+b(k≠0)与二次函数y=ax2(a≠0)的图象相交于点A(-1,1),B(2,4),则关于x的方程ax2=kx+b的解为 .
14.(2023·山东招远期中)用总长为a米的材料做成如图(1)所示的矩形窗框,设窗框的宽为x米,窗框的面积为y米2,y关于x的函数图象如图(2)所示,则a的值是 .
第14题图 第15题图
15.(2022·安徽蚌埠期末)如图,在平面直角坐标系中,点A,B的坐标分别为(-,2),
(,2),连接AB.已知抛物线y=(x-h)2.
(1)当抛物线同时经过A,B点时,h的值为 ;
(2)若抛物线与线段AB有公共点,则h的取值范围是 .
选择题、填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12.
13. 14. 15.(1) (2)
三、解答题(共6小题,共55分)
16.(7分)(2023·广东珠海香洲区期中)已知抛物线y=x2-ax+2(a-3).
(1)求证:不论a为何实数,这个抛物线与x轴总有两个交点.
(2)如果抛物线与x轴的一个交点的坐标为(3,0),求a的值.
17.(8分)(2022·江苏苏州姑苏区期中)把抛物线C1:y=-x2-2x+3先向右平移4个单位长度,再向下平移5个单位长度得到抛物线C2.
(1)求抛物线C2的解析式.
(2)点P(a,1)是否在抛物线C2上 请说明理由.
18.(9分)(2022·安徽安庆期中)某小区计划建一个矩形花圃,花圃的一边利用长为a米的墙,另三边用总长为79米的篱笆围成,围成的花圃是如图所示的矩形ABCD,并在BC边上留有一扇1米宽的门.设AD边的长为x米,矩形花圃的面积为S米2.
(1)求S与x之间的函数关系式.(不要求写出自变量x的取值范围)
(2)若a=30,求S的最大值.
19.(10分) (2023·河南洛阳伊滨区段考)某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x … -3 - -2 -1 0 1 2 3 …
y … 3 m -1 0 -1 0 3 …
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2-2|x|=0有 个实数根;
②方程x2-2|x|=2有 个实数根.
20.(10分)(2023·浙江绍兴越城区期中)商店以每件40元的价格购进一种商品,经
市场调查发现:在一段时间内,该商品的日销售量y(件)与售价x(元/件)成一次函数
关系,其对应关系如表.
售价/(元/件) 45 50 60
日销售量/件 110 100 80
(1)求y关于x的函数表达式.
(2)求售价为多少时,日销售利润w最大,最大利润是多少元.
(3)该商店准备搞节日促销活动,顾客每购买一件该商品奖m元(m>0),若在日销售量
不少于68件时的日销售最大利润是1 360元,且日销售量与售价仍然满足(1)中的函数关系式,求m的值.(每件的销售利润=售价-进价)
21.(11分)如图,在平面直角坐标系xOy中,已知抛物线y=-x2+2x+3与x轴交于A,B两点,与y轴交于点D,抛物线的顶点为E,且C,D两点关于抛物线的对称轴对称,直线y=kx+b经过A,C两点.
(1)求直线AC的解析式.
(2)设点P是直线AC上方抛物线上的一动点,当△PAC的面积取得最大值时,求出此时点P的坐标.
(3)若点M在此抛物线上,点N在抛物线的对称轴上,则以A,C,M,N为顶点的四边形能否构成以AC为边的平行四边形 若能,请直接写出所有满足要求的点M的坐标;若不能,请说明理由.
第二十二章 二次函数
选择题、填空题答案速查
1 2 3 4 5 6 7 8 9 10
D A C C D B D C D A
11.< 12.y=x2-4(或y=x2-4x+4,答案不唯一) 13.x1=-1,x2=2
14.12 15.(1) (2)-≤h≤
1.D y=x2+8x-9=x2+8x+16-9-16=(x+4) 2-25.
2.A ∵y=(m+2)x|m|+2是y关于x的二次函数,∴|m|=2且m+2≠0,解得m=2.
3.C 分析如下:
y=-2x2 图象开口向下 图象有最高点 图象对称轴是y轴 当x>0时,y随x的增大而减小,当x<0时,y随x的增大而增大
y=x2 图象开口向上 图象有最低点 图象对称轴是y轴 当x>0时,y随x的增大而增大,当x<0时,y随x的增大而减小
y=3x2 图象开口向上 图象有最低点 图象对称轴是y轴 当x>0时,y随x的增大而增大,当x<0时,y随x的增大而减小
y=-x2 图象开口向下 图象有最高点 图象对称轴是y轴 当x>0时,y随x的增大而减小,当x<0时,y随x的增大而增大
4.C ∵抛物线经过点A(1,n)和点B(3,n),∴抛物线的对称轴为直线x==2,即-=2,解得b=4.
5.D ∵抛物线y=(x-3)2+c经过点A(2,0),∴(2-3)2+c=0,解得c=-1.∴抛物线的解析式为y=(x-3)2-1.令y=0,即(x-3)2-1=0.解得x=2或x=4.∴该抛物线与x轴的另一个交点坐标为(4,0).
∵抛物线的对称轴为直线x=3,抛物线与x轴的一个交点坐标为(2,0),∴由抛物线的对称性可知,抛物线与x轴的另一个交点坐标为(4,0).
6.B ∵函数图象与y轴正半轴相交,∴y轴在抛物线与x轴的两个交点之间,∴点B,C可能是原点.∵当x<0时,y随x的增大而增大,∴y轴在抛物线顶点左侧,∴点B可能是原点.
7.D 原式可化为y=(x-3)2-4,可知二次函数图象的顶点坐标为(3,-4).因为2<3<6,所以最小值m=-4.当y=0时,x2-6x+5=0,解得x1=1,x2=5.如图,当x=6时,y=36-36+5=5,即n=5.则n-m=5-(-4)=9.
8.C s=54t-t2=-(t-18)2+486,∵-<0,抛物线开口向下,∴当t=18时,s取得最大值,此时s=486.∵飞机滑行到最大距离时停下来,此时滑行时间也为最大值,∴t=18.
9.D (转化思想)如图,设点M为抛物线y1的顶点,点N为抛物线y2的顶点,连接MA,
NB,则四边形AMNB的面积和阴影部分的面积相等.由题意得AB∥MN,AB=MN=2,∴四边形AMNB是平行四边形.∵抛物线y1=(x+1)2-3,∴顶点M的坐标为(-1,-3),∴点M到x轴的距离为3,∴平行四边形AMNB的面积是2×3=6,∴阴影部分的面积是6.
10.A (分类讨论思想)当0
11.<
12.y=x2-4(或y=x2-4x+4,答案不唯一) 设二次函数y=x2的图象沿y轴平移后得到y=x2+b的图象.∵经过点(2,0),∴0=4+b,解得b=-4,∴沿y轴平移后所得图象对应的函数解析式是y=x2-4.设二次函数y=x2的图象沿x轴平移后得到y=(x-a)2的图象,将(2,0)代入,解得a=2,∴沿x轴平移后所得图象对应的函数解析式是y=(x-2)2=x2-
4x+4.
13.x1=-1,x2=2 ∵一次函数y=kx+b(k≠0)与二次函数y=ax2(a≠0)的图象相交于点A(-1,1),B(2,4),∴关于x的方程ax2=kx+b的解为x1=-1,x2=2.
14.12 由图象可知,当x=2时,y取得最大值,且最大值为4,∴窗框的最大面积是4米2.根据矩形面积计算公式,得窗框的另一边的长为4÷2=2(米),∴材料总长a=
3×2+3×2=12(米).
15.(1) (2)-≤h≤ (1)易知抛物线y=(x-h)2的对称轴为直线x=h,当抛物线同时经过点A(-,2),B(,2)时,抛物线的对称轴为直线x==,∴h=.(2)当抛物线经过A点时,可得2=(--h)2,解得h=-或;当抛物线经过B点时,可得2=(-h)2,解得h=或.故抛物线与线段AB有公共点,则h的取值范围是-≤h≤.
16.【参考答案】(1)证明:Δ=a2-8(a-3)=a2-8a+24=a2-8a+16+8=(a-4)2+8>0,
则不论a为何实数,这个抛物线与x轴总有两个交点. (4分)
(2)把(3,0)代入得9-3a+2(a-3)=0,
解得a=3. (7分)
17.【参考答案】(1)∵y=-x2-2x+3=-(x+1)2+4,
∴把抛物线C1:y=-x2-2x+3先向右平移4个单位长度,再向下平移5个单位长度得到抛物线C2:y=-(x+1-4)2+4-5,即y=-(x-3)2-1, (3分)
∴抛物线C2的解析式为y=-(x-3)2-1. (4分)
(2)不在. (5分)
理由:∵抛物线C2的解析式为y=-(x-3)2-1,
∴该函数的最大值为-1. (7分)
∵点P的纵坐标为1,且1>-1,
∴点P(a,1)不在抛物线C2上. (8分)
18.【参考答案】(1)AB边的长为=(40-x)(米),
根据题意得S=(40-x)x=-x2+40x, (3分)
∴S与x之间的函数关系式为S=-x2+40x. (4分)
(2)由(1)知S=-x2+40x=-(x-40)2+800,(5分)
∵-<0,
∴当x≤40时,S随x的增大而增大.
∵x≤a,a=30,
∴当x=30时,S取得最大值,最大值为750.(9分)
19.【参考答案】(1)0 (2分)
解法提示:把x=-2代入y=x2-2|x|,得y=0,
所以m=0.
(2)如图所示.
(5分)
(3)①函数y=x2-2|x|的图象关于y轴对称;
②当x>1时,y随x的增大而增大.(答案不唯一)(7分)
(4)①3 3 (9分)
②2 (10分)
20.【参考答案】(1)设y关于x的函数关系式为y=kx+b,
由题意得
解得
故y关于x的函数关系式是y=-2x+200(40
故当售价是70元/件时,日销售利润w最大,最大利润是1 800元. (6分)
(3)由题意得-2x+200≥68,
∴x≤66,
∴日销量利润w=(-2x+200)(x-40-m)=-2x2+(2m+280)x-8 000-200m(40
∴>70.
∵-2<0,
∴w关于x的函数的图象所在的抛物线开口向下,对称轴为直线x=.
∵x≤66<70,
∴w随x的增大而增大,
∴当x=66时,w取得最大值,最大值为(-2×66+200)(66-40-m)=68(26-m),
∴68(26-m)=1 360,
∴m=6. (10分)
21.【参考答案】(1)对于y=-x2+2x+3,令x=0,则y=3,
令-x2+2x+3=0,解得x=-1或3,
故点A,B,D的坐标分别为(-1,0),(3,0),(0,3),抛物线的对称轴为直线x=1. (2分)
∵C,D两点关于抛物线的对称轴x=1对称,D(0,3),
∴C(2,3).
将点A,C的坐标分别代入y=kx+b,得解得
故直线AC的解析式为y=x+1. (4分)
(2)如图,过点P作y轴的平行线交AC于点H. (5分)
设P(t,-t2+2t+3),则H(t,t+1),
S△PAC=S△PHA+S△PHC=PH·(xC-xA).
∵A,C点的位置已确定,
∴当PH的值最大时,S△PAC最大.
PH=-t2+2t+3-t-1=-t2+t+2,
∵-1<0,
∴当t=-=时,△PAC的面积取得最大值,
此时点P的纵坐标为-()2+2×+3=,
故点P的坐标为(,). (8分)
(3)点M的坐标为(-2,-5)或(4,-5). (11分)
(3)解法提示:画示意图如图所示,
∵A(-1,0),C(2,3),
∴点A,C之间的水平距离为3.
∵平行四边形以AC为边,
∴由平行四边形的性质知,点M,N的水平距离为3.
又点N在对称轴x=1上,
∴点N的横坐标为1,
∴点M的横坐标为-2或4.
∵点M在抛物线上,
∴将点M的横坐标代入即可得点M的坐标为(-2,-5)或(4,-5).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
