第二十四章 圆单元测试卷（含答案）

中小学教育资源及组卷应用平台
2025人教版九年级数学上册
第二十四章　圆
时间 90分钟　满分 100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)　　　　　 　　　　　　　　　　　　　　
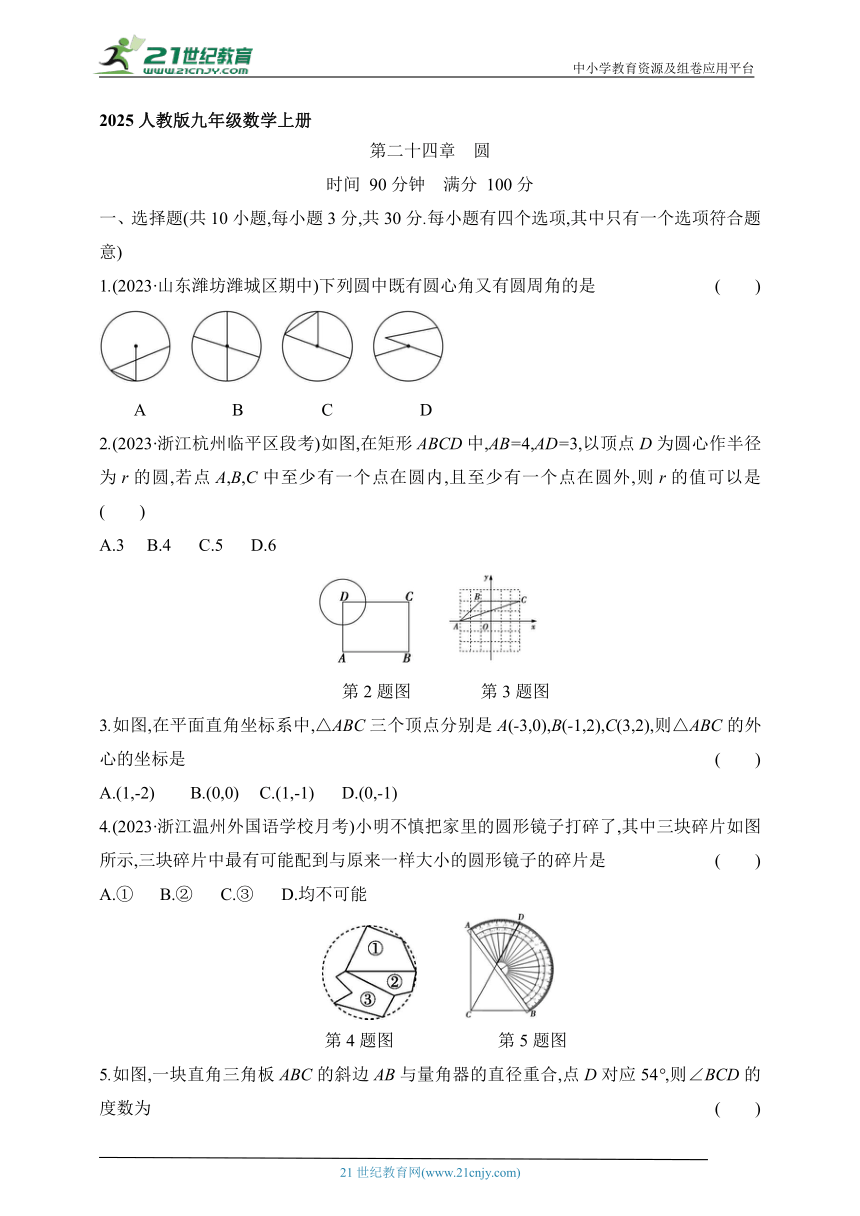
1.(2023·山东潍坊潍城区期中)下列圆中既有圆心角又有圆周角的是 (　　)
A B C D
2.(2023·浙江杭州临平区段考)如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的值可以是(　　)
A.3 B.4 C.5 D.6
　　
第2题图 第3题图
3.如图,在平面直角坐标系中,△ABC三个顶点分别是A(-3,0),B(-1,2),C(3,2),则△ABC的外心的坐标是 (　　)
A.(1,-2) B.(0,0) C.(1,-1) D.(0,-1)
4.(2023·浙江温州外国语学校月考)小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是 (　　)
A.① B.② C.③ D.均不可能
　 　
第4题图 第5题图
5.如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为 (　　)
A.27° B.54° C.63° D.36°
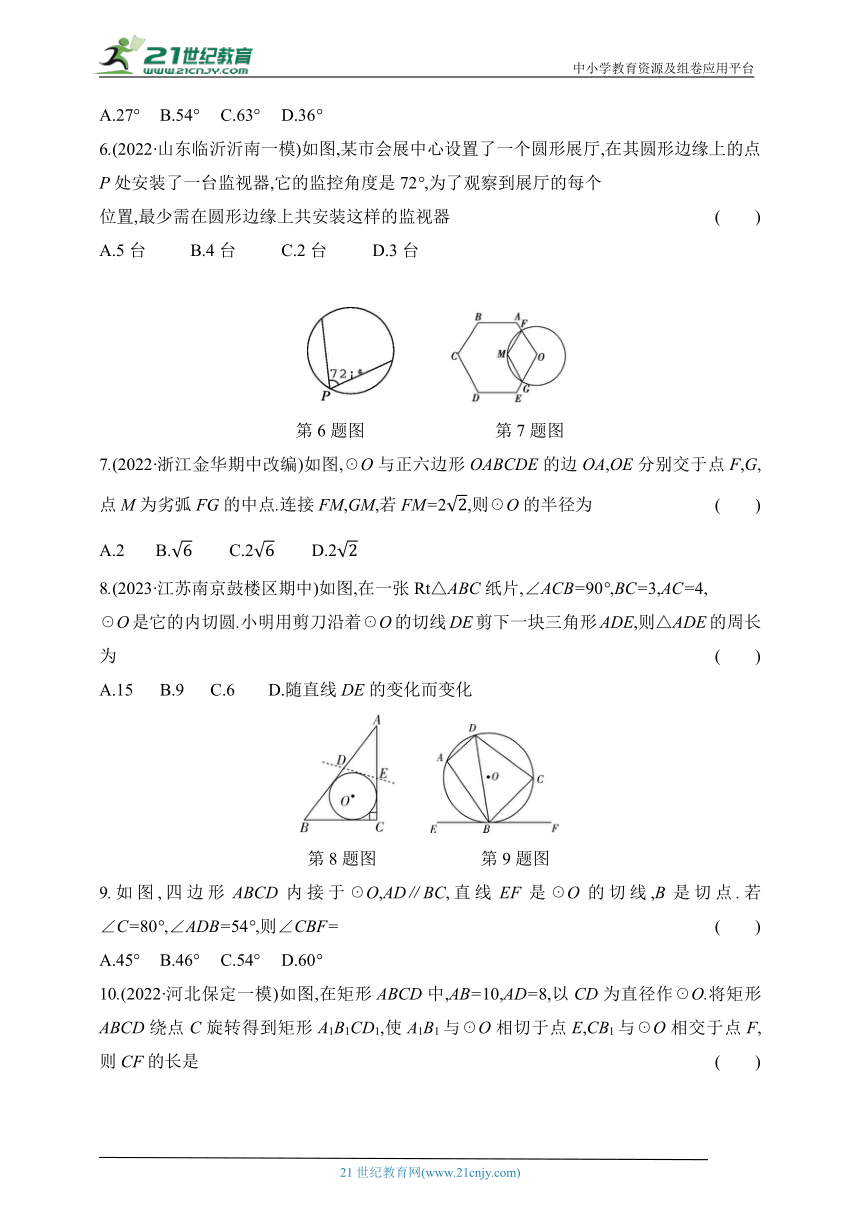
6.(2022·山东临沂沂南一模)如图,某市会展中心设置了一个圆形展厅,在其圆形边缘上的点P处安装了一台监视器,它的监控角度是72°,为了观察到展厅的每个
位置,最少需在圆形边缘上共安装这样的监视器 (　　)
A.5台　 B.4台　 C.2台　 D.3台
　　　　
第6题图 第7题图
7.(2022·浙江金华期中改编)如图,☉O与正六边形OABCDE的边OA,OE分别交于点F,G,点M为劣弧FG的中点.连接FM,GM,若FM=2,则☉O的半径为 (　　)
A.2 B. C.2 D.2
8.(2023·江苏南京鼓楼区期中)如图,在一张Rt△ABC纸片,∠ACB=90°,BC=3,AC=4,
☉O是它的内切圆.小明用剪刀沿着☉O的切线DE剪下一块三角形ADE,则△ADE的周长为 (　　)
A.15 B.9 C.6 D.随直线DE的变化而变化
　　
第8题图 　第9题图
9.如图,四边形ABCD内接于☉O,AD∥BC,直线EF是☉O的切线,B是切点.若∠C=80°,∠ADB=54°,则∠CBF= (　　)
A.45° B.46° C.54° D.60°
10.(2022·河北保定一模)如图,在矩形ABCD中,AB=10,AD=8,以CD为直径作☉O.将矩形ABCD绕点C旋转得到矩形A1B1CD1,使A1B1与☉O相切于点E,CB1与☉O相交于点F,则CF的长是 (　　)
A.3　 B.4　 C.6　 D.8
二、填空题(共5小题,每小题3分,共15分)
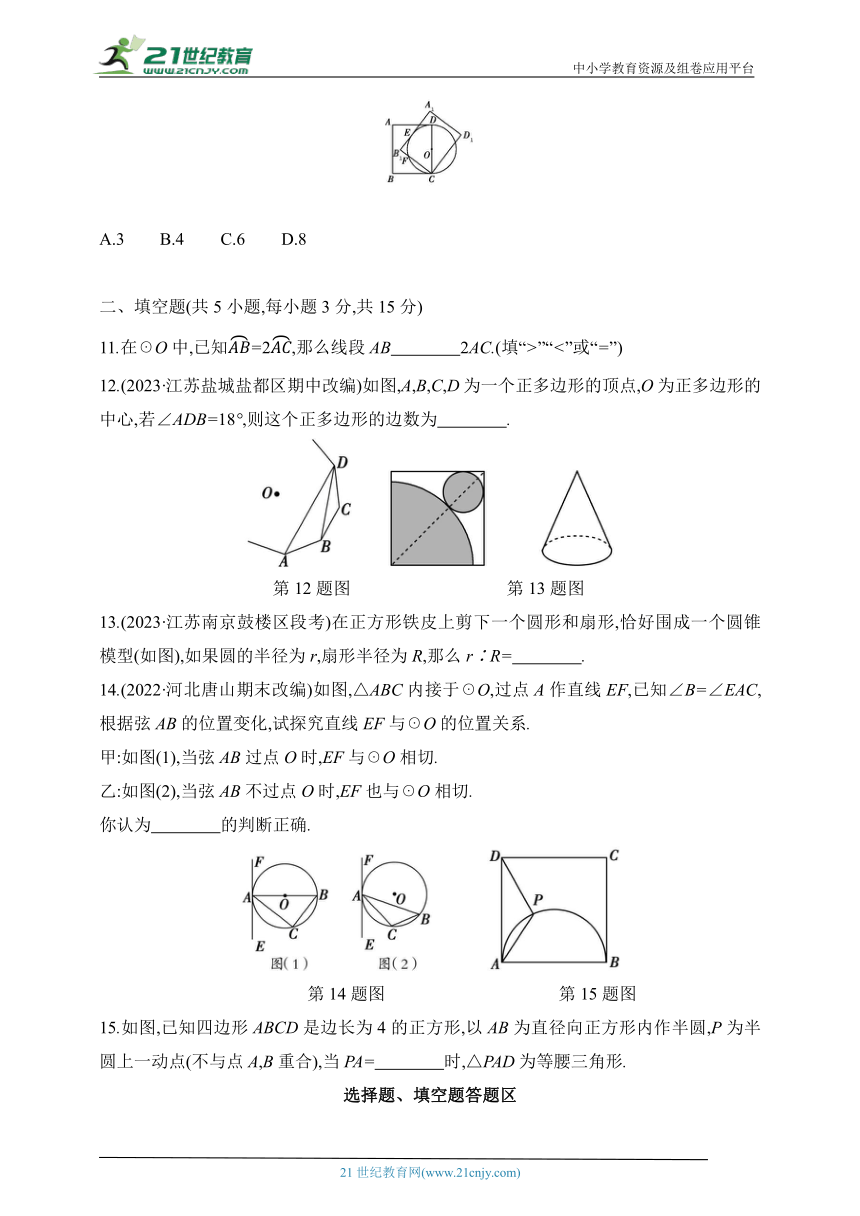
11.在☉O中,已知=2,那么线段AB　　　　2AC.(填“>”“<”或“=”)
12.(2023·江苏盐城盐都区期中改编)如图,A,B,C,D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=18°,则这个正多边形的边数为　　　　.
　　
第12题图 第13题图
13.(2023·江苏南京鼓楼区段考)在正方形铁皮上剪下一个圆形和扇形,恰好围成一个圆锥模型(如图),如果圆的半径为r,扇形半径为R,那么r∶R=　　　　.
14.(2022·河北唐山期末改编)如图,△ABC内接于☉O,过点A作直线EF,已知∠B=∠EAC,根据弦AB的位置变化,试探究直线EF与☉O的位置关系.
甲:如图(1),当弦AB过点O时,EF与☉O相切.
乙:如图(2),当弦AB不过点O时,EF也与☉O相切.
你认为　　　　的判断正确.
　　　
第14题图 第15题图
15.如图,已知四边形ABCD是边长为4的正方形,以AB为直径向正方形内作半圆,P为半圆上一动点(不与点A,B重合),当PA=　　　　时,△PAD为等腰三角形.
选择题、填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12.
13. 14. 15.
三、解答题(共6小题,共55分)
16.(6分)在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,
埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何.”用现代语言表述
为:如图,AB为☉O的直径,弦CD⊥AB于点E,AE=1寸,CD=10寸,求直径AB的长.请你解答这个问题.
17.(7分)(2022·北京人大附中朝阳学校期中)《几何原本》是古希腊数学家欧几里得所著的一部数学著作.下面是《几何原本》第三卷的第30个命题“二等分已知弧”的作图过程.请你根据要求回答下面的问题.
命题:二等分已知弧.
几何语言:如图,已知,求作的中点C.
作法:①连接AB;②作弦AB的垂直平分线,交于点C,交弦AB于点D;③连接AC,BC;④则点C就是的中点.
问题:
(1)使用直尺和圆规,补全图形(保留作图痕迹).
(2)写出上述作图过程的两条依据:
① ;
② 　.
18.(9分)(2022·山东临沂期末)如图,AB为☉O的直径,AC,DC为弦,∠ACD=60°,P为AB延长线上的点,连接PD,∠APD=30°.
(1)求证:DP是☉O的切线.
(2)若☉O的半径为2,求图中阴影部分的面积.
19.(10分)(2023·山东潍坊颍州区段考)如图,☉O为等边△ABC的外接圆,半径为2,点D在劣弧AB上运动(不与点A,B重合),连接DA,DB,DC.
(1)求证:DC是∠ADB的平分线.
(2)若将△ADC绕点C逆时针旋转60°得到△BHC,则四边形ADBC的面积S是线段CD的长x的函数吗 如果是,求出函数解析式,并写出x的范围;如果不是,请说明理由.
20.(11分)某种在同一平面进行传动的机械装置如图(1)所示,图(2)是它的示意图,其工作原理是:滑块Q在平直滑道l上可以左右滑动,在Q滑动的过程中,连杆PQ也随之运动,并且PQ带动连杆OP绕固定点O摆动.在摆动过程中,两连杆的接点P在以OP为半径的☉O上运动.数学兴趣小组为进一步研究其中的数学知识,过点O作OH⊥l于点H,并测得OH=4分米,PQ=3分米,OP=2分米.
解决问题
(1)点Q与点O之间的最小距离是　　　　分米,最大距离是 分米.
(2)如图(3),小明说:“当点Q滑动到点H的位置上时,PQ与☉O相切.”你认为他的说法对吗 为什么
(3)当OP绕点O左右摆动时,所扫过的区域为扇形,求扇形的最大面积.
　　　　　　　　　
图(1)　 图(2)
图(3)　　　　　　　　备用图
21.(12分)【问题呈现】阿基米德折弦定理:如图(1),AB和BC是☉O的两条弦(即折线ABC是☉O的一条折弦),BC>AB,M是的中点,则从点M向BC作垂线,垂足D是折弦ABC的中点,即CD=AB+BD.下面是运用“截长法”证明CD=AB+BD的过程.
证明:如图(2),在CD上截取CG=AB,连接MA,MB,MC和MG.
∵M是的中点,∴MA=MC.①
∵∠A=∠C,②
∴△MAB≌△MCG,
∴MB=MG.
又MD⊥BC,∴BD=DG,
∴CD=CG+DG=AB+BD,即CD=AB+BD.
根据证明过程,分别写出步骤①,②的理由:
①　　　　　　　　.②　　　　　　　　.
【理解运用】在图(1)中,若AB=4,BC=6,则BD=　　　　.
【变式探究】如图(3),AB,BC是☉O的两条弦,点M是的中点,MD⊥BC于点D,请写出CD,DB,BA之间存在的数量关系:　　　　　.
【实践应用】如图(4),△ABC内接于☉O,BC是☉O的直径,点D为圆周上一点,满足∠DAC=45°.若AB=6,☉O的半径为5,求AD的长.
　
图(1)　　　　 　图(2)
　
图(3)　　　　 　 图(4)
第二十四章　圆
选择题、填空题答案速查
1 2 3 4 5 6 7 8 9 10
C B A A C D D C B C
11.< 12.10 13.1∶4
14.甲、乙 15.2或
1.C　A选项图中只有圆周角,没有圆心角;B选项图中只有圆心角,没有圆周角;C选项图中既有圆心角,又有圆周角;D选项图中只有圆心角,没有圆周角.故选C.
2.B　连接BD,由勾股定理可得BD===5,由题意可知,3判断点和圆的位置关系的实质是判断点到圆心的距离与半径的大小关系.
3.A　
如图,∵三角形的外心到三角形三个顶点的距离都相等,∴线段BC,AB的垂直平分线的交点P即为外心,由图可知,点P的坐标为(1,-2).
4.A　第①块出现两条完整的弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径.故选A.
5.C　∵一块直角三角板ABC的斜边AB与量角器的直径重合,∴点A,B,C,D都在以AB为直径的圆上.设此圆圆心为点O,连接OD.∵点D对应54°,即∠AOD=54°,
∴∠ACD=∠AOD=27°,∴∠BCD=90°-∠ACD=63°.
6.D　由题意可知,一台监视器所对应的圆心角为72°×2=144°,∵360°÷
144°=2.5,∴至少需要3台.故选D.
7.D　连接OM,由题意知∠FOG=120°.∵点M为劣弧FG的中点,∴∠FOM=60°.
∵OM=OF,∴△OFM是等边三角形,∴OM=OF=FM=2,则☉O的半径为2,故选D.
8.C　如图,设△ABC的内切圆切三边于点F,H,G,连接OF,OH,OG,∴四边形OHCG是正方形,由切线长定理可知AF=AG,∵DE是☉O的切线,∴MD=DF,EM=EG.∵∠ACB=90°,
BC=3,AC=4,∴AB==5.∵☉O是△ABC的内切圆,∴内切圆的半径=(AC+BC-
AB)=1,∴CG=1,∴AG=AC-CG=4-1=3,∴△ADE的周长AD+DE+AE=AD+DF+EG+AE=AF+AG=
2AG=6.
9.B　如图,连接OD,OB,则∠BOD=2∠C=160°.∵OB=OD,∴∠OBD==10°.∵四边形ABCD内接于☉O,∴∠A=180°-∠C=100°.∵AD∥BC,∴∠A+∠ABC=180°,
∴∠ABC=80°.在△ABD,∠ADB=54°,∴∠ABD=180°-54°-100°=26°,∴∠OBC=
80°-26°-10°=44°.∵EF是☉O的切线,∴∠OBF=90°,∴∠CBF=90°-∠OBC=
90°-44°=46°.故选B.
∵AD∥BC,∴∠ADB+∠BDC+∠C=180°.∵∠C=80°,∠ADB=54°,∴∠BDC=46°.∵∠CBF是弦切角,∴∠CBF=∠BDC=46°.(弦切角定理:弦切角的度数等于它所夹的弧所对的圆心角度数的一半,等于它所夹的弧所对的圆周角度数)
10.C　如图,连接OE,作OH⊥B1C于点H,∵A1B1与☉O相切于点E,∴∠OEB1=∠OHB1=
90°,∵矩形ABCD绕点C旋转得到矩形A1B1CD1,∴∠B1=∠B1CD1=90°,AB=CD=10,BC=
B1C=AD=8,∴四边形OEB1H是矩形,OE=OD=OC=5,∴B1H=OE=5,∴CH=B1C-B1H=3,∴CF=
2CH=6.故选C.
11.<　如图,∵=2,∴=,∴AC=BC. ∵AC+BC>AB,∴AB<2AC.
12.10　如图,连接OA,OB,由题意知点A,B,C,D均在以点O为圆心,OA为半径的圆上.∵∠ADB=18°,∴∠AOB=2∠ADB=36°,∴这个正多边形的边数=360°÷36°=
10.
13.1∶4　由题意可得×2πR=2πr,所以R=4r,所以r∶R=1∶4.
14.甲、乙　题图(1)中,∵AB是☉O的直径,∴∠C=90°,∴∠B+∠CAB=90°.
∵∠EAC=∠B,∴∠EAC+∠CAB=90°,∴EF⊥AB.∵OA是半径,∴EF是☉O的切线,故甲的判断正确.如图,作直径AM,连接CM,则∠ACM=90°,∠B=∠M.∵∠EAC=∠B,
∴∠EAC=∠M.∵∠CAM+∠M=90°,∴∠CAM+∠EAC=90°,∴EF⊥AO,∵AO是☉O的半径,∴EF是☉O的切线,故乙的判断正确.
15.2或
△PAD为等腰三角形—
AP=2AG=←AG=←S△DAO=DA·AO=DO·AG
16.【参考答案】连接OC(图略).
∵CD⊥AB,AB为☉O的直径,CD=10寸,
∴CE=DE=CD=5寸. (3分)
设OC=OA=x寸,得AB=2OA=2x寸,则OE=(x-1)寸.
由勾股定理,得OE2+CE2=OC2,即(x-1)2+52=x2,
解得x=13,
∴AB=26寸, (5分)
故直径AB的长为26寸. (6分)
17.【参考答案】(1)如图,C点即所作. (3分)
(2)①平分弦(不是直径)的直径垂直于这条弦,并且平分这条弦所对的两条弧
②线段垂直平分线上的点到线段两端点的距离相等
(或在同一个圆中,如果弦相等,那么它们所对应的弧相等) (7分)
18.【参考答案】(1)证明:如图,连接OD.
∵∠ACD=60°,
∴∠AOD=120°,∴∠BOD=60°.
∵∠APD=30°,
∴∠ODP=90°,即PD⊥OD.
∵OD是半径,
∴PD是☉O的切线. (5分)
(2)∵在Rt△POD中,OD=2,∠OPD=30°,
∴OP=4.
由勾股定理得PD=2.
∴S阴影部分=S△POD-S扇形ODB=×2×2-=2-. (9分)
19.【参考答案】(1)证明:∵△ABC是等边三角形,
∴∠ABC=∠BAC=∠ACB=60°.
∵∠ADC=∠ABC=60°,∠BDC=∠BAC=60°,
∴∠ADC=∠BDC,
∴DC是∠ADB的平分线. (4分)
(2)四边形ADBC的面积S是线段CD的长x的函数.
如图,将△ADC绕点C逆时针旋转60°得到△BHC,
则CD=CH,∠DAC=∠HBC,
∵四边形ADBC是圆内接四边形,
∴∠DAC+∠DBC=180°,
∴∠DBC+∠HBC=180°,
∴D,B,H三点共线.
∵CD=CH,∠CDH=60°,
∴△DCH是等边三角形,
∵四边形ADBC的面积S=S△ADC+S△BDC=S△CDH=CD2,
∴S=x2(220.【参考答案】(1)4　5 (2分)
(2)不对. (3分)
理由:∵42≠32+22,即OQ2≠PQ2+OP2,
∴OP与PQ不垂直,
∴PQ与☉O不相切. (7分)
(3)∵PQ的长度固定,为3分米,
∴只有PQ⊥l时,点P到OH的距离最大.
设点P在左侧的最远位置为P1,在右侧的最远位置为P2,如图.
过点P2作P2M⊥OH于点M,
则HM=P2Q=3分米,
∴OM=4-3=1(分米).
在Rt△OP2M中,OP2=2分米,OM=1分米,
∴∠MOP2=60°,
∴∠P1OP2=120°,
∴==(分米2).
故扇形的最大面积是平方分米. (11分)
21.【参考答案】【问题呈现】①在同圆中,如果两条弧相等,那么它们所对的弦相等
②同弧所对的圆周角相等 (4分)
【理解运用】1 (6分)
解法提示:∵CD=AB+BD,∴CD=(AB+BC)=×(4+6)=5,∴BD=BC-CD=6-5=1.
【变式探究】DB=AB+CD (8分)
解法提示:如图,在DB上截取BG=BA,连接MA,MB,MC,MG.
∵M是的中点,∴AM=MC,∠MBA=∠MBG.
又MB=MB,∴△MAB≌△MGB,
∴MA=MG,∴MC=MG.
又DM⊥BC,∴DC=DG,
∴AB+DC=BG+DG,
即DB=AB+CD.
【实践应用】∵BC是☉O的直径,∴∠BAC=90°.
∵AB=6,☉O的半径为5,∴易得AC=8.
(分类讨论思想)如图,当∠DAC=45°时,有两种情况.
①当D与D1重合时,∠D1AC=45°,则D1是的中点.
过点D1作D1G1⊥AC于点G1,易得CG1+AB=AG1.
∴AG1=(AB+AC)=×(6+8)=7,∴AD1=AG1=7.
②当D与D2重合时,∠D2AC=45°,过点D2作D2G2⊥AC于点G2,同理易得CG2=AB+AG2,
∴CG2=(AB+AC)=7,AG2=1,∴AD2=.
综上,AD的长为7或. (12分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)