第二十一章 一元二次方程单元测试卷(含答案)
文档属性
| 名称 | 第二十一章 一元二次方程单元测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 323.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-11 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025人教版九年级数学上册
第二十一章 一元二次方程
时间 90分钟 满分 100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.(2023·武汉青山区期中)将一元二次方程2x2+1=5x化成一般形式后,一次项系数、常数项分别为 ( )
A.1,-5 B.-5,1 C.1,5 D.5,1
2.(2022·北京西城区期中)若(m-1)x|m|+1-2x=3是关于x的一元二次方程,则m的值为 ( )
A.-1 B.1 C.±1 D.无法确定
3.(2023·大连期末)用配方法解方程x2-4x=-2,下列配方正确的是 ( )
A.(x-2)2=2 B.(x+2)2=2
C.(x-2)2=-2 D.(x-2)2=0
4.若4a-2b+c=0,则一元二次方程ax2-bx+c=0(a≠0)必有一根是 ( )
A.0 B.无法确定 C.-2 D.2
5.若2x2+1与4x2-2x-5互为相反数,则x= ( )
A.-1或 B.1或-
C.1或- D.1或
6.(2023·河北邢台五中月考)用直接开平方法解一元二次方程(x-1)2=9的步骤如下:
①(x-1)2=36,②x-1=±6,③x=±7,④即x1=7,x2=-7.
其中开始错误的步骤是 ( )
A.① B.② C.③ D.④
7.(2023·福建漳州期中)若a*b=ab2-2ab-3.则方程3*x=0的根的情况为 ( )
A.无实数根 B.有两个相等的实数根
C.有两个不相等的实数根 D.不能确定
8.生物学家研究发现,很多植物的生长都有下面的规律,即主干长出若干数目的枝子后,每个枝子又会长出同样数目的小枝子.现有符合上述生长规律的某种植物,它的主干、枝子和小枝子的总数是91,则这种植物每个枝子长出小枝子的个数是 ( )
A.9 B.10 C.-10 D.9或10
9.(2023·江苏高邮期中)若关于x的一元二次方程a(x+m)2+n=0(a≠0)的两根分别为-2,1,则关于x的一元二次方程a(x+m-2 022)2+n=0(a≠0)的两根分别为 ( )
A.x1=-2,x2=1 B.x1=2 020,x2=2 023
C.x1=-2 020,x2=2 023 D.x1=-2 024,x2=-2 019
10.(2022·厦门六中期末)欧几里得的《几何原本》中记载,形如x2+ax=b2的方程的图解法是:画Rt△ABC,使∠ACB=90°,BC=,AC=b,再在斜边AB上截取BD=.则该方程的一个正根是 ( )
A.AC的长 B.AD的长 C.BC的长 D.CD的长
二、填空题(共5小题,每小题3分,共15分)
11.已知关于x的一元二次方程x2-mx=0的一个根为1,则m= .
12.(2023·北京首都师大附中段考)请写出一个满足以下两个条件的一元二次方程:①两根均为整数;②两根异号.
这个方程可以是 .
13.(2023·深圳南山区期末)若m,n是一元二次方程x2+2 022x-2 023=0的两个实数根,则+= .
14.(2022·江西南昌段考)在2022年7月的日历表上用一个方框圈出4个数(如图所示),若圈出的4个数中,最小数与最大数的乘积为180,则这个最小数 .
15.小刚在解关于x的方程ax2+bx+c=0(a≠0)时,只抄对了a=1,b=3,解出其中一个根是x=-1.他核对时发现所抄的c值比原方程的c值小2,则
(1)原方程中c= ;
(2)原方程的根的情况是 .
选择题、填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12.
13. 14. 15.(1) (2)
三、解答题(共6小题,共55分)
16.(共3小题,每小题4分,共12分)用适当的方法解下列方程:
(1)y(y-1)=2-2y;
(2)5x2-8x=-5;
(3)(x+2)2-8(x+2)+15=0.
17.(8分)(2023·湖南武冈期中)已知关于x的一元二次方程(a+c)x2+2bx+a-c=0,其中a,b,c分别为△ABC三边的长.
(1)如果x=-1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.
18.(8分)(2023·保定17中期中)“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然正气”.某校为响应全民阅读活动,在周六面向社会开放学校图书馆.据统计,该校图书馆第一个月进馆256人次,第三个月进馆576人次,假设进馆人次的月平均增长率相同.
(1)求进馆人次的月平均增长率;
(2)因条件限制,学校图书馆每月接纳不超过1 000人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否正常接纳第四个月的进馆人次 请说明理由.
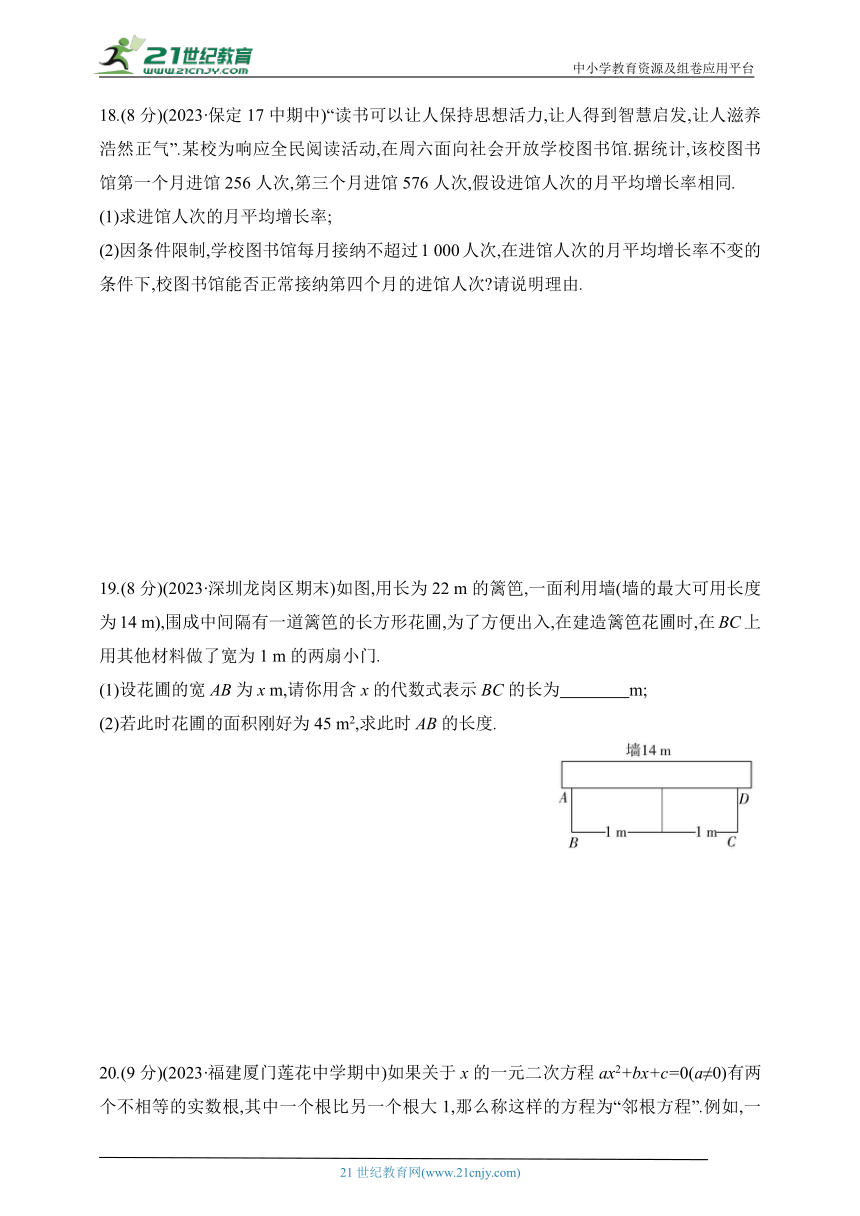
19.(8分)(2023·深圳龙岗区期末)如图,用长为22 m的篱笆,一面利用墙(墙的最大可用长度为14 m),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC上用其他材料做了宽为1 m的两扇小门.
(1)设花圃的宽AB为x m,请你用含x的代数式表示BC的长为 m;
(2)若此时花圃的面积刚好为45 m2,求此时AB的长度.
20.(9分)(2023·福建厦门莲花中学期中)如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个不相等的实数根,其中一个根比另一个根大1,那么称这样的方程为“邻根方程”.例如,一元二次方程x2+x=0的两个实数根分别是x1=0,
x2=-1,则方程x2+x=0是“邻根方程”.
(1)通过计算,判断方程2x2-2x+1=0是不是“邻根方程”.
(2)已知关于x的方程x2-(m-1)x-m=0(m是常数)是“邻根方程”,求m的值.
21.(10分)(2022·河南洛阳期中)阅读并完成下列问题:任意给定一个矩形A,是否存在另一矩形B,使它的周长和面积分别是已知矩形周长和面积的一半
(1)当已知矩形A的相邻两边长分别为6和1时,小亮同学是这样研究的:
设所求矩形的相邻两边长分别是x和y,由题意可得方程组
消去y,得2x2-7x+6=0.
∵Δ=49-48=1>0,
∴x1= ,x2= ,
∴满足要求的矩形B存在.
(2)如果已知矩形A的相邻两边长分别为2和1,那么请你仿照小亮的方法研究是否存在满足要求的矩形B.
(3)如果矩形A的相邻两边长分别为m和n,那么请你研究当m,n满足什么条件时,矩形B存在,并说明理由.
第二十一章 一元二次方程
选择题、填空题答案速查
1 2 3 4 5 6 7 8 9 10
B A A D B C C A B B
11.1 12.x2+2x-3=0(答案不唯一)
13. 14.10 15.(1)4 (2)没有实数根
1.B 将一元二次方程2x2+1=5x化成一般形式为2x2-5x+1=0,故一次项系数、常数项分别为-5,1.
2.A 由题意得|m|+1=2,且m-1≠0,解得m=-1.
3.A x2-4x+4=-2+4,(x-2)2=2.
4.D ∵4a-2b+c=0,∴a×22-b×2+c=0,∴方程ax2-bx+c=0(a≠0)必有一根为2.
5.B 由题意可得2x2+1+4x2-2x-5=0,即3x2-x-2=0,解得x=1或-.
6.C (x-1)2=9,(x-1)2=36,x-1=±6,x1=6+1=7,x2=-6+1=-5.
7.C 利用题中的新定义化简得3x2-6x-3=0,∵Δ=(-6)2-4×3×(-3)=36+36=72>0,
∴方程有两个不相等的实数根.
8.A 设这种植物每个枝子长出x个小枝子,依题意可得枝子的数量为x,小枝子的数量为x·x=x2,根据题意可列出方程1+x+x2=91,解得x1=9,x2=-10(舍去),故这种植物每个枝子长出9个小枝子.
9.B 把关于x的一元二次方程a(x+m-2 022)2+n=0看作为关于(x-2 022)的一元二次方程,∵关于x的一元二次方程a(x+m)2+n=0(a≠0)的两根分别为-2,1,∴x-2 022=
-2或x-2 022=1,解得x1=2 020,x2=2 023,即关于x的一元二次方程a(x+m-2 022)2+
n=0(a≠0)的两根分别为x1=2 020,x2=2 023.
10.B Rt△ABC中,∠ACB=90°,BC=,AC=b,BD=,设AD=x,则AB=x+,根据勾股定理得AB2=AC2+BC2,即(x+)2=b2+()2,整理得x2+ax-b2=0(a≠0,b≠0).∵Δ=a2+4b2>0,∴方程有两个不相等的实数根,且两根之积等于-b2<0,即方程的根为一正一负,则该方程的一个正根是AD的长.
11.1 把x=1代入方程x2-mx=0,得1-m=0,解得m=1.
12.x2+2x-3=0(答案不唯一) 本题答案不唯一,只要满足两根之积小于0且两根均为整数即可.
13. ∵m,n是一元二次方程x2+2 022x-2 023=0的两个实数根,∴m+n=-2 022,
mn=-2 023,∴+===.
14.10 设这个最小数为x,则最大数为(x+8),根据题意得x(x+8)=180,整理得x2+8x-
180=0,解得x1=10,x2=-18(不合题意,舍去),所以这个最小数为10.
15.(1)4 (2)没有实数根 (1)∵小刚在解关于x的方程ax2+bx+c=0(a≠0)时,只抄对了a=1,b=3,解出其中一个根是x=-1,∴(-1)2-3+c=0,解得c=2,故原方程中c=4.(2)易得Δ=9-4×1×4=-7<0,∴原方程的根的情况是没有实数根.
16.【参考答案】(1)移项,得y(y-1)+2(y-1)=0, (2分)
因式分解,得(y+2)(y-1)=0,
解得y1=-2,y2=1. (4分)
(2)移项,得5x2-8x+5=0.
因为a=5,b=-8,c=5,
所以Δ=b2-4ac=64-100=-36<0, (2分)
所以方程无实数根. (4分)
(3)(整体思想)把(x+2)看成一个整体,
因式分解,得[(x+2)-3][(x+2)-5]=0, (2分)
整理,得(x-1)(x-3)=0,
解得x1=1,x2=3. (4分)
17.【参考答案】(1)△ABC是等腰三角形. (1分)
理由:∵x=-1是方程的根,
∴(a+c)×(-1)2-2b+a-c=0,
∴a+c-2b+a-c=0,
∴a-b=0,
∴a=b,
∴△ABC是等腰三角形. (4分)
(2)△ABC是直角三角形. (5分)
理由:∵方程有两个相等的实数根,
∴Δ=(2b)2-4(a+c)(a-c)=0,
∴4b2-4a2+4c2=0,
∴a2=b2+c2,
∴△ABC是直角三角形. (8分)
18.【参考答案】(1)设进馆人次的月平均增长率为x,
根据题意得256(1+x)2=576,
解得x1=0.5=50%,x2=-2.5(不合题意,舍去).
答:进馆人次的月平均增长率是50%. (4分)
(2)能. (5分)
理由:576×(1+50%)=864(人次),
∵864<1 000,
∴校图书馆能正常接纳第四个月的进馆人次. (8分)
19.【参考答案】(1)(24-3x)(2分)
(2)由题意得x(24-3x)=45 (4分)
化简得x2-8x+15=0,
解得x1=5,x2=3. (6分)
当x=5时,24-3x=9<14,符合要求;
当x=3时,24-3x=15>14,不符合要求,舍去.
答:花圃的宽AB为5 m. (8分)
20.【参考答案】(1)是. (1分)
理由:Δ=(-2)2-4×2×1=4>0,故方程有两个不相等的实数根.
解一元二次方程,得x1=,x2=. (3分)
∵-=1,
∴方程2x2-2x+1=0是“邻根方程”. (5分)
(2)解方程,得x=m或x=-1. (6分)
∵方程x2-(m-1)x-m=0(m是常数)是“邻根方程”,
∴|m-(-1)|=1,
∴m=-1+1或m=-1-1, (8分)
解得m=0或-2. (9分)
21.【参考答案】(1) 2 (2分)
(2)设所求矩形的相邻两边长分别是a和b,
由题意,得
消去b,得2a2-3a+2=0.
∵Δ=9-16=-7<0,
∴此方程无解,
∴不存在满足要求的矩形B. (5分)
(3)当m,n满足(m-n)2-4mn≥0时,矩形B存在.(6分)
理由如下:
设所求矩形的相邻两边长分别是p和q,
由题意,得
消去q,得2p2-(m+n)p+mn=0, (7分)
∴Δ=[-(m+n)]2-8mn=(m-n)2-4mn.
当Δ≥0时,存在满足要求的矩形B,
即当(m-n)2-4mn≥0时,矩形B存在. (10分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教版九年级数学上册
第二十一章 一元二次方程
时间 90分钟 满分 100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.(2023·武汉青山区期中)将一元二次方程2x2+1=5x化成一般形式后,一次项系数、常数项分别为 ( )
A.1,-5 B.-5,1 C.1,5 D.5,1
2.(2022·北京西城区期中)若(m-1)x|m|+1-2x=3是关于x的一元二次方程,则m的值为 ( )
A.-1 B.1 C.±1 D.无法确定
3.(2023·大连期末)用配方法解方程x2-4x=-2,下列配方正确的是 ( )
A.(x-2)2=2 B.(x+2)2=2
C.(x-2)2=-2 D.(x-2)2=0
4.若4a-2b+c=0,则一元二次方程ax2-bx+c=0(a≠0)必有一根是 ( )
A.0 B.无法确定 C.-2 D.2
5.若2x2+1与4x2-2x-5互为相反数,则x= ( )
A.-1或 B.1或-
C.1或- D.1或
6.(2023·河北邢台五中月考)用直接开平方法解一元二次方程(x-1)2=9的步骤如下:
①(x-1)2=36,②x-1=±6,③x=±7,④即x1=7,x2=-7.
其中开始错误的步骤是 ( )
A.① B.② C.③ D.④
7.(2023·福建漳州期中)若a*b=ab2-2ab-3.则方程3*x=0的根的情况为 ( )
A.无实数根 B.有两个相等的实数根
C.有两个不相等的实数根 D.不能确定
8.生物学家研究发现,很多植物的生长都有下面的规律,即主干长出若干数目的枝子后,每个枝子又会长出同样数目的小枝子.现有符合上述生长规律的某种植物,它的主干、枝子和小枝子的总数是91,则这种植物每个枝子长出小枝子的个数是 ( )
A.9 B.10 C.-10 D.9或10
9.(2023·江苏高邮期中)若关于x的一元二次方程a(x+m)2+n=0(a≠0)的两根分别为-2,1,则关于x的一元二次方程a(x+m-2 022)2+n=0(a≠0)的两根分别为 ( )
A.x1=-2,x2=1 B.x1=2 020,x2=2 023
C.x1=-2 020,x2=2 023 D.x1=-2 024,x2=-2 019
10.(2022·厦门六中期末)欧几里得的《几何原本》中记载,形如x2+ax=b2的方程的图解法是:画Rt△ABC,使∠ACB=90°,BC=,AC=b,再在斜边AB上截取BD=.则该方程的一个正根是 ( )
A.AC的长 B.AD的长 C.BC的长 D.CD的长
二、填空题(共5小题,每小题3分,共15分)
11.已知关于x的一元二次方程x2-mx=0的一个根为1,则m= .
12.(2023·北京首都师大附中段考)请写出一个满足以下两个条件的一元二次方程:①两根均为整数;②两根异号.
这个方程可以是 .
13.(2023·深圳南山区期末)若m,n是一元二次方程x2+2 022x-2 023=0的两个实数根,则+= .
14.(2022·江西南昌段考)在2022年7月的日历表上用一个方框圈出4个数(如图所示),若圈出的4个数中,最小数与最大数的乘积为180,则这个最小数 .
15.小刚在解关于x的方程ax2+bx+c=0(a≠0)时,只抄对了a=1,b=3,解出其中一个根是x=-1.他核对时发现所抄的c值比原方程的c值小2,则
(1)原方程中c= ;
(2)原方程的根的情况是 .
选择题、填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12.
13. 14. 15.(1) (2)
三、解答题(共6小题,共55分)
16.(共3小题,每小题4分,共12分)用适当的方法解下列方程:
(1)y(y-1)=2-2y;
(2)5x2-8x=-5;
(3)(x+2)2-8(x+2)+15=0.
17.(8分)(2023·湖南武冈期中)已知关于x的一元二次方程(a+c)x2+2bx+a-c=0,其中a,b,c分别为△ABC三边的长.
(1)如果x=-1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.
18.(8分)(2023·保定17中期中)“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然正气”.某校为响应全民阅读活动,在周六面向社会开放学校图书馆.据统计,该校图书馆第一个月进馆256人次,第三个月进馆576人次,假设进馆人次的月平均增长率相同.
(1)求进馆人次的月平均增长率;
(2)因条件限制,学校图书馆每月接纳不超过1 000人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否正常接纳第四个月的进馆人次 请说明理由.
19.(8分)(2023·深圳龙岗区期末)如图,用长为22 m的篱笆,一面利用墙(墙的最大可用长度为14 m),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC上用其他材料做了宽为1 m的两扇小门.
(1)设花圃的宽AB为x m,请你用含x的代数式表示BC的长为 m;
(2)若此时花圃的面积刚好为45 m2,求此时AB的长度.
20.(9分)(2023·福建厦门莲花中学期中)如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个不相等的实数根,其中一个根比另一个根大1,那么称这样的方程为“邻根方程”.例如,一元二次方程x2+x=0的两个实数根分别是x1=0,
x2=-1,则方程x2+x=0是“邻根方程”.
(1)通过计算,判断方程2x2-2x+1=0是不是“邻根方程”.
(2)已知关于x的方程x2-(m-1)x-m=0(m是常数)是“邻根方程”,求m的值.
21.(10分)(2022·河南洛阳期中)阅读并完成下列问题:任意给定一个矩形A,是否存在另一矩形B,使它的周长和面积分别是已知矩形周长和面积的一半
(1)当已知矩形A的相邻两边长分别为6和1时,小亮同学是这样研究的:
设所求矩形的相邻两边长分别是x和y,由题意可得方程组
消去y,得2x2-7x+6=0.
∵Δ=49-48=1>0,
∴x1= ,x2= ,
∴满足要求的矩形B存在.
(2)如果已知矩形A的相邻两边长分别为2和1,那么请你仿照小亮的方法研究是否存在满足要求的矩形B.
(3)如果矩形A的相邻两边长分别为m和n,那么请你研究当m,n满足什么条件时,矩形B存在,并说明理由.
第二十一章 一元二次方程
选择题、填空题答案速查
1 2 3 4 5 6 7 8 9 10
B A A D B C C A B B
11.1 12.x2+2x-3=0(答案不唯一)
13. 14.10 15.(1)4 (2)没有实数根
1.B 将一元二次方程2x2+1=5x化成一般形式为2x2-5x+1=0,故一次项系数、常数项分别为-5,1.
2.A 由题意得|m|+1=2,且m-1≠0,解得m=-1.
3.A x2-4x+4=-2+4,(x-2)2=2.
4.D ∵4a-2b+c=0,∴a×22-b×2+c=0,∴方程ax2-bx+c=0(a≠0)必有一根为2.
5.B 由题意可得2x2+1+4x2-2x-5=0,即3x2-x-2=0,解得x=1或-.
6.C (x-1)2=9,(x-1)2=36,x-1=±6,x1=6+1=7,x2=-6+1=-5.
7.C 利用题中的新定义化简得3x2-6x-3=0,∵Δ=(-6)2-4×3×(-3)=36+36=72>0,
∴方程有两个不相等的实数根.
8.A 设这种植物每个枝子长出x个小枝子,依题意可得枝子的数量为x,小枝子的数量为x·x=x2,根据题意可列出方程1+x+x2=91,解得x1=9,x2=-10(舍去),故这种植物每个枝子长出9个小枝子.
9.B 把关于x的一元二次方程a(x+m-2 022)2+n=0看作为关于(x-2 022)的一元二次方程,∵关于x的一元二次方程a(x+m)2+n=0(a≠0)的两根分别为-2,1,∴x-2 022=
-2或x-2 022=1,解得x1=2 020,x2=2 023,即关于x的一元二次方程a(x+m-2 022)2+
n=0(a≠0)的两根分别为x1=2 020,x2=2 023.
10.B Rt△ABC中,∠ACB=90°,BC=,AC=b,BD=,设AD=x,则AB=x+,根据勾股定理得AB2=AC2+BC2,即(x+)2=b2+()2,整理得x2+ax-b2=0(a≠0,b≠0).∵Δ=a2+4b2>0,∴方程有两个不相等的实数根,且两根之积等于-b2<0,即方程的根为一正一负,则该方程的一个正根是AD的长.
11.1 把x=1代入方程x2-mx=0,得1-m=0,解得m=1.
12.x2+2x-3=0(答案不唯一) 本题答案不唯一,只要满足两根之积小于0且两根均为整数即可.
13. ∵m,n是一元二次方程x2+2 022x-2 023=0的两个实数根,∴m+n=-2 022,
mn=-2 023,∴+===.
14.10 设这个最小数为x,则最大数为(x+8),根据题意得x(x+8)=180,整理得x2+8x-
180=0,解得x1=10,x2=-18(不合题意,舍去),所以这个最小数为10.
15.(1)4 (2)没有实数根 (1)∵小刚在解关于x的方程ax2+bx+c=0(a≠0)时,只抄对了a=1,b=3,解出其中一个根是x=-1,∴(-1)2-3+c=0,解得c=2,故原方程中c=4.(2)易得Δ=9-4×1×4=-7<0,∴原方程的根的情况是没有实数根.
16.【参考答案】(1)移项,得y(y-1)+2(y-1)=0, (2分)
因式分解,得(y+2)(y-1)=0,
解得y1=-2,y2=1. (4分)
(2)移项,得5x2-8x+5=0.
因为a=5,b=-8,c=5,
所以Δ=b2-4ac=64-100=-36<0, (2分)
所以方程无实数根. (4分)
(3)(整体思想)把(x+2)看成一个整体,
因式分解,得[(x+2)-3][(x+2)-5]=0, (2分)
整理,得(x-1)(x-3)=0,
解得x1=1,x2=3. (4分)
17.【参考答案】(1)△ABC是等腰三角形. (1分)
理由:∵x=-1是方程的根,
∴(a+c)×(-1)2-2b+a-c=0,
∴a+c-2b+a-c=0,
∴a-b=0,
∴a=b,
∴△ABC是等腰三角形. (4分)
(2)△ABC是直角三角形. (5分)
理由:∵方程有两个相等的实数根,
∴Δ=(2b)2-4(a+c)(a-c)=0,
∴4b2-4a2+4c2=0,
∴a2=b2+c2,
∴△ABC是直角三角形. (8分)
18.【参考答案】(1)设进馆人次的月平均增长率为x,
根据题意得256(1+x)2=576,
解得x1=0.5=50%,x2=-2.5(不合题意,舍去).
答:进馆人次的月平均增长率是50%. (4分)
(2)能. (5分)
理由:576×(1+50%)=864(人次),
∵864<1 000,
∴校图书馆能正常接纳第四个月的进馆人次. (8分)
19.【参考答案】(1)(24-3x)(2分)
(2)由题意得x(24-3x)=45 (4分)
化简得x2-8x+15=0,
解得x1=5,x2=3. (6分)
当x=5时,24-3x=9<14,符合要求;
当x=3时,24-3x=15>14,不符合要求,舍去.
答:花圃的宽AB为5 m. (8分)
20.【参考答案】(1)是. (1分)
理由:Δ=(-2)2-4×2×1=4>0,故方程有两个不相等的实数根.
解一元二次方程,得x1=,x2=. (3分)
∵-=1,
∴方程2x2-2x+1=0是“邻根方程”. (5分)
(2)解方程,得x=m或x=-1. (6分)
∵方程x2-(m-1)x-m=0(m是常数)是“邻根方程”,
∴|m-(-1)|=1,
∴m=-1+1或m=-1-1, (8分)
解得m=0或-2. (9分)
21.【参考答案】(1) 2 (2分)
(2)设所求矩形的相邻两边长分别是a和b,
由题意,得
消去b,得2a2-3a+2=0.
∵Δ=9-16=-7<0,
∴此方程无解,
∴不存在满足要求的矩形B. (5分)
(3)当m,n满足(m-n)2-4mn≥0时,矩形B存在.(6分)
理由如下:
设所求矩形的相邻两边长分别是p和q,
由题意,得
消去q,得2p2-(m+n)p+mn=0, (7分)
∴Δ=[-(m+n)]2-8mn=(m-n)2-4mn.
当Δ≥0时,存在满足要求的矩形B,
即当(m-n)2-4mn≥0时,矩形B存在. (10分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
